Open Journal of Fluid Dynamics
Vol.05 No.02(2015), Article ID:56836,6 pages
10.4236/ojfd.2015.52012
The Relation between the Coefficient of Friction and Pressure Drop by Using the Different Reynolds Number in a Circular Tube
Abdulmagid A. Khattabi1, Ahmed A. Hablous2, Mofied M. Elnemry3
1Department of Mechanical Engineering, Higher Institute of Marine Sciences Techniques and Fisheries, Sabrata, Libya
2Department of Mechanical Engineering, Higher Institute of Industrial Technology, Tripoli, Libya
3College of Engineering Technology, Janzor, Libya
Email: mazalib@yahoo.com, hablous@yahoo.com, mofeednemri@yahoo.co.uk
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 March 2015; accepted 30 May 2015; published 2 June 2015
ABSTRACT
This study explains the relationship between friction coefficient and pressure change at a range of Reynolds (21,056 - 28,574) and (0 - 1.4) solid loading ratio of two-phase flow (gas-solid) inside a circular copper pipe by using laboratory apparatus and solving the equations mathematically. An experimentally relationship of friction coefficient and pressure change with Reynolds number and flow velocity obtained also the relationship between the Solid loading ratio with friction coefficient and pressure change has been done for a Limit range of Reynolds number. It was noticed that the increase in friction coefficient and pressure change for two-phase flow was occurred when solid loading ratio increased. Also the relationship between pressure change and Reynolds number was direct proportion while the relationship between friction coefficient and Reynolds Number was inversely related.
Keywords:
Two-Phase Flow, Pressure Drop, Reynolds Number, Loading Ratio, Friction Coefficient

1. Introduction
One phase flow is caused due to the difference in pressure from region to the other this lets the air particles move from the high-pressure area to the low area. The fluid speed directly proportional to the amount of pressure drop depends on the dimensions and shape of the space passing through the fluid [1] . Therefore two-phase flows are widely used in most of the engineering disciplines. Researchers at the beginning of modern industry have noted this phenomenon and found that have many applications as what is applied in energy production, materials factories producing and chemical factories. Dogen et al. (2006) [2] presented a study of the theory to calculate pressure drop losses for multiple phases of fluids through the use of a mathematical model that was developed using account program works at the expense of losses through nozzle flux area. Results obtained compared with the results of other models were found less than 10%. Researchers (P. H. Morten Sen, H. I. Andersson) [3] presented a practical study shows the friction process of two-phase flow (R410A-oil) inside the tube with very small spiral fins. These results showed a pressure drop caused by friction depending on the properties of the mixture [4] and [5] . Current research aims to practically study the two-phase flow (gas-solid) inside a circular pipe section for purpose to reach the relationship coefficient of friction and pressure drop with speed, Reynolds number and loading rate.
2. Practical Side
The components for two-phase flow testing must be mounted to each other and on the same horizontal line because any deviation will change the direction of fluid.
The length of the device from the beginning (4.5 m) and at altitudes (1 m) above the ground level. Laboratory device consists unit of inflatable air (pump), injection unit to inject the solid particles which consists plastic reservoir where placed solid particles (sand material) containing slot from the top to fill the tank. The measurement unit of air flow rate is composed of a copper tube inner diameter (25.5 m) is installed in the internal nozzle (Orifice). Necessary equipment to complete this research as Figure 1.
3. Laboratory Calculations
The air mass flow rate ṁa is calculated by measuring the total pressure across the orifice by manometer mmH2O units, as follows:
To calculate the speed of the air through the nozzle
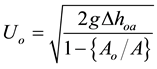 (1)
(1)
To calculate the volumetric air flow Q in units of m3/sec we use the following equation.
 (2)
(2)
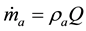 (3)
(3)
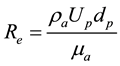 (4)
(4)
The amount of solid particles calculated as follows:
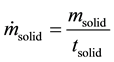 (5)
(5)
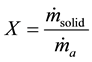 (6)
(6)
where X is loading ratio.
The amount of pressure drop calculated as a result of friction between the mixture and tube walls [6] as follows:
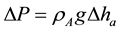 (7)
(7)
By applying (Darcy equation) to Calculate the coefficient of friction (Yunus, et al.) [7]
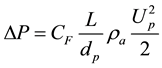 (8)
(8)
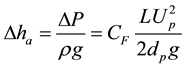 (9)
(9)
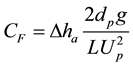 (10)
(10)
4. Test Procedure
The recorded readings below are based on the sequence to get accuracy in calculations as follows:
・ Measuring weather conditions of pressure and temperature, because its effect on the density of air.
・ The device is turned on and then changes the amount of air entering slot to determine how much the speed of the airflow rate and the corresponding difference in the vertical height of the water in the manometer and record it.
・ Measuring loading ratio: Measure loading ratio by passing the solid particles to get two-phase mixture after a period of time and after reaching stability the time required to collect a certain mass of solid particles measured by using stopwatch.
・ After completion of the above stages, repeat these tests for all velocities for the purpose of recording all the reading of the various flow of material amounts and rates of speed.
5. Results and Discussion
After conducting tests and recording the required measurements, such as the amount of pressure inside the copper tube and knowing the system dimensions (length and diameter of the tube, air density) can extract the following amounts (Re, Cf, U and Δp ) . Figure 2 represents the relationship between pressure drop and flow velocity of Turbulence two-phase flow where noted on the chart that is a positive relationship between flow velocity of Turbulence two-phase flow and pressure drop because the amount of pressure drop in the tube depends on the speed of the fluid flow inside the tube. Figure 3 shows the relationship between the Reynolds number and the pressure drop where noted that the pressure drop increasing with Reynolds number as a result of increased flow velocity inside the tube. Figure 4 and Figure 5 illustrate the relationship between the coefficient of friction with the flow velocity and Reynolds number as the inverse relationship. The reason that there are two forces that
Figure 1. Necessary equipment to complete this research.
Figure 2. Pressure drop versus flow velocity of turbulent two-phase flow.
Figure 3. Pressure drop versus Reynolds numbers.
Figure 4. Flow velocity versus friction coefficient.
Figure 5. Friction coefficient versus Reynolds numbers.
Figure 6. Friction coefficient versus loading rate for different values of Reynolds numbers.
Figure 7. Pressure drop versus loading rate for different values of Reynolds numbers.
affected on the movement of particle the two forces is the momentum and shear strength Figure 6 shows the relationship between the coefficient of friction and loading rates of two-phase flow were used several rates of air flow (Reynolds number from (21,056 to 28,574). The coefficient of friction increasing with increase of loading rate. And noted that when the increase of Reynolds number the friction rate decreases, Figure 7 represents the relationship of pressure drop and the percentage of solid loading for different values of the Reynolds number it can be note that the amount of pressure drop increases by increasing of the proportion of solid loading. By noting several curves for different values of Reynolds number can note that as increasing in Reynolds number, the pressure drop will increase at the same solid loading ratio.
6. Conclusions and Recommendation
Results have been reached in this research, which includes practices study of two-phase flow inside a copper pipe and by using various different (Reynolds number) and different amounts of loading rates, the conclusions are as follows:
1) The relationship between pressure drop and flow velocity and Reynolds number is a positive correlation.
2) Increasing the amount of Reynolds number or flow velocity makes the friction coefficient of two-phase flow decrease.
3) Friction coefficient and pressure drop of two-phase flow increase due to increasing of solid loading ratio.
4) It is possible to make several changes to develop the test equipment and get other study cases:
・ Test the other section as a box shape.
・ Test other types of solid particles.
・ Conduct the study using pipes with different degrees of roughness and record the amount degree of roughness.
References
- Wallis, G.B. (1969) One-Dimensional Two-Phase Flow.
- Dogen, H.A. (2006) A Comprehensive Bit Hydraulics Model for Gasified Drilling Fluids.
- Mortensen, P.H., Andersson, H.I., Gillissen, J.J.J. and Boersma, B.J. (2008) On the Orientation of Ellipsoidal Particles in a Turbulent Shear Flow. International Journal of Multiphase Flow, 34, 678-683. http://dx.doi.org/10.1016/j.ijmultiphaseflow.2007.12.007
- Ding, G.L., Hu, H.T., Huang, X.C., Deng, B. and Gao, Y.F. (2009) Experimental Investigation and Correlation of Two-Phase Frictional Pressure Drop of R410A―Oil Mixture Flow Boiling in a 5 mm Microfin Tube. International Journal of Refrigeration, 32, 150-161. http://dx.doi.org/10.1016/j.ijrefrig.2008.08.009
- Fan, J., Hu, C.B., He, G.Q. and Yang, Y.X. (2009) Study of Two-Phase Loss in Gas-Solid Flow. 45th AIAA/ASME/ SAE/ASEE Joint Propulsion Conference & Exhibit, 2-5 August 2009. http://dx.doi.org/10.2514/6.2009-4979
- White, F.M. (2000) Fluid Mechanics. 4th Edition.
- Cengel, Y.A. and Turner, R.H. (2003) Fundamentals of Thermal-Fluid Sciences.
List of Symbols
Cf Friction coefficient
dp tube diameter m
g gravity m/s2
L length m
ṁa air mass flow rate kg/sec
msolid mass of solid particles kg
msolid solid particles flow rate kg/sec
Q volume flow rate m3/sec
Re Reynolds number
tsolid The time required for the collection of solid particles sec
Uo The speed of two-phase mixture m/sec
Up Speed biphasic mixture in the tube m/sec
X steel loading kg solid/kg gas
ρa air density kg/m3
μa Air viscosity kg/m・sec
Δha loses due friction m
Δhoa Air column different across both sides of the crater m
Δp Pressure drop along the tube pa








