Open Journal of Fluid Dynamics
Vol.04 No.05(2014), Article ID:52843,9 pages
10.4236/ojfd.2014.45031
Comparison of One-Dimensional Analysis with Experiment for CO2 Two-Phase Nozzle Flow
Wakana Tsuru, Satoshi Ueno, Yoichi Kinoue, Norimasa Shiomi
Department of Mechanical Engineering, Saga University, Saga, Japan
Email: kinoue@me.saga-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 October 2014; revised 6 November 2014; accepted 5 December 2014
ABSTRACT
The aim of this study is to investigate CO2 two-phase nozzle flow in terms of both experimental and analytical aspects for the optimum design of two-phase flow nozzle of CO2 two-phase flow ejector. In the experiment, it is measured that the temperature profile in the stream-wise direction of a divergent-convergent nozzle through which CO2 in the supercritical pressure condition is blown down into the atmosphere. In the analysis, a one-dimensional model which assumes steady, adiabatic, frictionless, and equilibrium is proposed. In the convergent part of the nozzle the flow is treated as single-phase flow of liquid, whereas in the divergent part the flow is treated as separated two-phase flow with saturated condition. The analytical results indicate that the temperature and the pressure decrease rapidly in the divergent part, and the void fraction increases immediately near the throat. Although this analysis is quite simple, the analytical results can follow the experimental results well within this study.
Keywords:
Carbon Dioxide, High-Speed Nozzle Flow, Gas-Liquid Two-Phase Flow with Phase Change, Blow down Test, One-Dimensional Analysis

1. Introduction
In recent years, natural refrigerants are regarded as refrigerants of refrigeration cycles. Because of the highly safety and the small global warming coefficient, carbon dioxide (CO2) is especially focused. However, wasted available energy which is discarded in a pressure reduction process at an expansion valve in the cycle of using CO2 is three times as much as that of using R-134a. Therefore, it is important to recover the available energy, and a gas-liquid two-phase flow ejector (two-phase flow ejector) is used to recover the energy [1] [2] .
A two-phase flow ejector consists of a driving flow nozzle, a suction chamber, a mixing section and a diffuser, respectively. Many researches for single-phase flow ejectors have been carried out. However for two-phase flow ejectors, the mechanisms of the internal flow with phase change have not been sufficiently made clear yet because of the complexly of the flow. This study is carried out on a gas-liquid two-phase flow nozzle (two-phase flow nozzle) of a driving nozzle flow section which is the most important section.
A divergent-convergent nozzle is generally used as a two-phase flow nozzle [3] . In actual CO2 refrigeration cycle, the typical value of the inlet pressure of the expansion valve is 9 MPa which exceeds the critical pressure of CO2, 7.38 MPa. Therefore, in a CO2 two-phase flow nozzle, the pressure of the nozzle inlet and the convergent section pressure are the supercritical pressure. And the flow in the divergent section is the saturated two- phase flow with phase change (boiling). The CO2 two-phase flow in the nozzle is a complicated high-speed flow with large changes in both temperature and pressure. For the optimum design of the nozzle which has these characteristics, the investigation of the fluid mechanics of the high speed gas-liquid two-phase flow is important.
For the two-phase nozzle flow there are studies conducted by Nakagawa et al. [3] -[6] . Nakagawa et al. investigated nozzle shapes experimentally [3] [4] , and proposed a one-dimensional analytical model for the flow [5] [6] . In their study, they analyzed a shock wave caused by a velocity relaxation and a temperature relaxation with the one-dimensional model. A phenomenon that the flow in the nozzle is not accelerated well owing to the existence of a shock wave has been explained by the analysis. On the other hand, it is necessary to analyze a phenomenon for the case that the flow in the nozzle accelerates and the pressure decreases sufficiently.
The purpose of this study is to conduct experimental and analytical investigations of the flow in the two-phase flow nozzle. In the experiment, in the similar way used by Nakagawa et al. [4] , the CO2 flow that goes through the divergent-convergent nozzle into the atmosphere is researched, where the temperature and the pressure distribution in the mainstream direction are investigated. In the analysis, one-dimensional analytical model assumed to be steady, adiabatic process, frictionless and equilibrium is investigated. The model refers to the formularization by Sudo and Katto [7] for the study of the critical flow rate of a compressible gas-liquid two-phase flow. A method to predict various distributions of flow properties along the mainstream is considered by solving fundamental equations, which are obtained from applying conservation of mass, momentum and energy to the flow in the two-phase flow nozzle, simultaneously.
2. Experimental Apparatus and Procedure
Figure 1 is the schematic diagram of experimental apparatus based on Nakagawa et al. [4] . The experimental apparatus mainly consists of a high-pressure tank and a test section. The high-pressure tank is filled up with gases in the order of CO2 and N2, and high-pressure CO2 can be obtained. The test section consists of the pressure measuring part at the nozzle inlet and the nozzle.
Figure 2 shows the rectangular nozzle [4] used for the nozzle part, where  is the distance from the nozzle inlet in the mainstream direction. Thermocouples are set on a side wall of the nozzle as shown in Figure 2, and the temperature inside the nozzle is measured. The pressure is calculated by using assumption of saturated condition and the measured temperature. CO2 is emitted through the test section into the atmosphere.
is the distance from the nozzle inlet in the mainstream direction. Thermocouples are set on a side wall of the nozzle as shown in Figure 2, and the temperature inside the nozzle is measured. The pressure is calculated by using assumption of saturated condition and the measured temperature. CO2 is emitted through the test section into the atmosphere.
The pressure in the high pressure tank is set four stages from 7.2 MPa to 10.3 MPa, and the CO2 gas is left until the tank temperature is the same temperature of the room of 300.15 K. At the time of starting the experiment, valve 3 and valve 4 in Figure 1 are opened to flow CO2 in the nozzle. The outputs of the thermocouples and the load cell are saved on a computer. The weight of the tank is measured at before and after the test, and the CO2 mass flow rate is calculated from the duration time of the emission.
3. One-Dimensional Analysis
3.1. Analytical Model
In the CO2 nozzle flow, the temperature and the pressure distributions change rapidly, and the phase condition changes from supercritical to saturated two-phase condition. To get the most important aspect of the complex flow, in this study, a one-dimensional analytical model is used. For this analysis, the flow is assumed to be steady, adiabatic, no friction and equilibrium.
The flow in the convergent part of the nozzle is treated as a single-phase flow. Figure 3 shows the single- phase flow model. Where 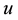 is the velocity,
is the velocity, 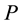 is the pressure,
is the pressure, 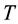 is the temperature,
is the temperature, 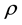 is the density,
is the density,
Figure 1. Experimental apparatus.
Figure 2. Details of nozzle.
Figure 3. Single-phase flow model for one- dimensional analysis.
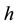 the enthalpy, and
the enthalpy, and 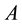 is the area of the cross section. Appling the laws of conservation of mass, momentum and energy to a minute section shown in Figure 3, Equations (1) to (3) is obtained,
is the area of the cross section. Appling the laws of conservation of mass, momentum and energy to a minute section shown in Figure 3, Equations (1) to (3) is obtained,
 (1)
(1)
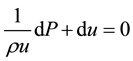 (2)
(2)
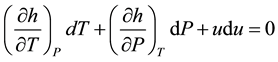 (3)
(3)
where  is positive. To obtain the temperature, the pressure and the velocity variations,
is positive. To obtain the temperature, the pressure and the velocity variations, 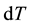 ,
, 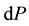 and
and
The flow in the divergent section is treated as a saturated separated two-phase flow. A model of the separated gas-liquid two-phase flow is shown in Figure 4. Appling the laws of conservation of mass, momentum and energy of each phase to a minute section as shown in Figure 4, Equations (4) to (7) is obtained,




where









In Figure 4 and Equations (4) to (7), the phase change model as changing from liquid to gas is applied to the minute mass flow rate, 

Simple and typical models of a gas-liquid two-phase flow are a separated flow model neglecting friction between the phases and a homogeneous flow model neglecting velocity difference between the phases. In the divergent section of the two-phase flow nozzle, since it is expected that the distribution of the void fraction changes significantly from 0 to 1, appropriate application of the two models is desirable. However, in this study, the whole flow in the divergent section of the two-phase flow nozzle is simply treated as a separated flow.
3.2. Analytical Object and Methods
The analysis is carried out on the flow in the convergent-divergent nozzle [4] shown in Figure 2. The flow in the rectangular nozzle that is 3 mm wide is analyzed in the mainstream direction. The nozzle that the total length
Figure 4. Two-phase flow model for one-di- mensional analysis.
is 84 mm is divided into 8400 cells (each section interval is 0.01 mm), and the flow is numerically analyzed by using fundamental equations which is appropriate for each section. There are not much difference between the results of the cases of 8400, 4200 and 16800 cells. Needed CO2 properties for the calculation process are obtained by PROPATH.
In the convergent section of the nozzle in which flow is treated as the single-phase flow, a flow which reached saturated condition is addressed as saturated liquid. Therefore, excluding 





4. Results and Discussions
4.1. Experimental Results
The experimental conditions at the nozzle inlet are listed in Table 1. The distribution of the temperature measured by the thermocouples in the mainstream direction is shown in Figure 5. The CO2 temperature in the nozzle decreases sharply, and in the case of the tank pressure of 7.2 MPa the difference in temperature between the inlet and the outlet is 80 K. As the tank pressure increases, the temperature at the nozzle outlet also increases. The nozzle outlet temperature for the tank pressure of 10.3 MPa is approximately 17 K larger than that of the tank pressure of 7.2 MPa.
Figure 6 shows the pressure distribution in the mainstream direction in the nozzle obtained by using the assumption of saturated condition and the temperature in Figure 5. The CO2 pressure decreases sharply in the nozzle as well as the temperature. Thus, it could be considered that CO2 accelerates sufficiently in the nozzle. As the tank pressure increases, the nozzle outlet pressure also increases. Regarding the nozzle outlet pressure, the one for the case of the tank pressure of 10.3 MPa is approximately 0.6 MPa larger than that of 7.2 MPa.
4.2. Comparison of Experiment and Analysis
The comparison of the experimental and the analytical results of the temperature distribution (a) or the pressure distribution (b) in the cases that the tank pressure is set to 7.2, 8.0, 9.2 and 10.3 MPa are shown in Figures 7-10.
In the case of the tank pressure of 7.2 MPa, as shown in Figure 7, the experimental and the analytical results can be considered almost the same. Since the condition of the nozzle inlet is approximately saturated, the flow in the convergent section of the nozzle is treated as saturated liquid.
In the case of the tank pressure of 8.0 MPa, as shown in Figure 8, the temperature distribution of the analysis is almost the same as that of the experiment. In the pressure distribution the analytical results in the convergent section are different from the experimental results, whereas, in the divergent section, the analytical results approximate to the experimental results. In the convergent section, since the critical pressure of CO2 is 7.38 MPa, it can be considered that the discrepancy is caused by the setting of the tank pressure to the supercritical pressure and the condition is not saturated in the experiment.
Regarding Figure 9 of the tank pressure of 9.2 MPa, for above reasons, the pressure difference between the experimental and the analytical results in the nozzle convergent section is caused. For the pressure in the divergent section and the temperature distribution of the analysis, the analytical results are rather smaller than the
Table 1. Experimental conditions.
Figure 5. Temperature distributions of experiment.
Figure 6. Pressure distributions of experiment.

Figure 7. Comparison of analysis with experiment (tank pressure = 7.2 MPa). (a) Temperature; (b) Pressure.

Figure 8. Comparison of analysis with experiment (tank pressure = 8.0 MPa). (a) Temperature; (b) Pressure.

Figure 9. Comparison of analysis with experiment (tank pressure = 9.2 MPa). (a) Temperature; (b) Pressure.

Figure 10. Comparison of analysis with experiment (tank pressure = 10.3 MPa). (a) Temperature; (b) Pressure.
experimental results around the throat. However, in area excepting the near throat, the analytical and the experimental results are approximately the same.
For the pressure in the divergent section and the temperature distribution in the case of the tank pressure of 10.3 MPa shown in Figure 10, the differences between the analytical and the experimental results at the near throat is larger than that of 9.2 MPa. Whereas, except the near throat, the analytical and the experimental results are well matched.
4.3. Analytical Results
Figures 11-14 show the analytical flow property distributions of the cases that the tank pressure set to 7.2, 8.0, 9.2 and 10.3 MPa, respectively. In Figures 11-14, the analytical results are marked with dotted line for cross sectional area, 




















where 

Figure 11. Analytical results (tank pressure = 7.2 MPa).
Figure 12. Analytical results (tank pressure = 8.0 MPa).
Figure 13. Analytical results (tank pressure = 9.2 MPa).
Figure 14. Analytical results (tank pressure = 10.3 MPa).
In the case of the tank pressure of 7.2 MPa, as shown in Figure 11, the quality, 






Compared with the sonic velocity defined in this paper, the gas-phase and the liquid-phase velocity is larger. From perspective of the sonic velocity defined in this paper, the flow in the divergent section can be considered as the supersonic flow.
In the case that the tank pressure is set to 8.0 MPa, as shown in Figure 12, general trend is the same as the tank pressure of 7.2 MPa. However, the velocity in the case of the tank pressure of 8.0 MPa is smaller than that of the case of 7.2 MPa despite the larger inlet velocity in the case of 8.0 MPa. As shown in Figure 13 and Figure 14, it can be considered that the higher pressure tank is set, the smaller velocity is calculated.
5. Summary
The flow field of the carbon dioxide high-speed two-phase nozzle flow has been investigated by the experiment and the one-dimensional analysis. Obtained results are as follows.
1) For the nozzle form used in this research and the experimental condition, the CO2 temperature and the pressure have been significantly and monotonously decreased in the nozzle, and satisfactory accelerating performance has been presumed.
2) For the nozzle flow, the one-dimensional analytical model which assumes to be steady, adiabatic, no friction and equilibrium is proposed. In this analytical model, the nozzle convergent section is assumed to be single- phase flow, and the nozzle divergent section is assumed to be separated gas-liquid two-phase flow.
3) The proposed analytical model is simple, and the assumption that the flow is the separated saturated gas- liquid two-phase flow does not necessarily satisfy the actual flow. However, in this experimental condition, these analytical results satisfactorily predicted these experimental results.
4) By the one-dimensional analysis, the velocity distribution in the mainstream direction in the nozzle is obtained, and the satisfactory accelerating performance has been indicated. Further, it is made clear that from the perspective of the sonic velocity defined in this analysis the flow in the divergent section can be considered as the supersonic flow.
References
- Nakagawa, M. (2004) Refrigeration Cycle with Two-Phase Ejector. Refrigeration, 79, 856-861.
- Akagi, S., Dang, C.B. and Hihara, E. (2006) Experimental Research of Two-Phase Ejector in Carbon Dioxide Heat Pump Cycle. Journals of Japan Society of Refrigerating and Air Conditioning Engineers, 23, 97-104.
- Nakagawa, M., Takeuchi, H. and Yokozaki, A. (1998) Performance of Two-Phase Nozzles Using the Refrigerant R134a. Transactions of Japan Society of Mechanical Engineers, Series B, 64, 3407-3413.
- Nakagawa, M., Takeuchi, H. and Berana, M.S. (2006) Supersonic Characteristics and Shock Waves in Two-Phase Flow along a Nozzle of a Carbon Dioxide Ejector. Proceedings of the 3rd Asian Conference on Refrigeration and Air-Conditioning, 1, 363-367.
- Nakagawa, M. and Sugiura, T. (2000) Shock Waves Caused by Velocity Relaxation in High Speed Mist Flow. Transactions of Japan Society of Mechanical Engineers, Series B, 66, 1495-1502.
- Sugiura, T. and Nakagawa, M. (2001) Shock Waves Caused by the Velocity and Temperature Relaxation of Subsonic Mist Flow in a Nozzle. Transactions of Japan Society of Mechanical Engineers, Series B, 67, 2462-2469.
- Sudo, Y. and Katto, Y. (1975) Study of Compressible Two-Phase Critical Flows: 1st Report, Principle of Occurrence of Critical Flow. Transactions of Japan Society of Mechanical Engineers, 41, 624-635. http://dx.doi.org/10.1299/kikai1938.41.624












