Open Journal of Fluid Dynamics
Vol.04 No.04(2014), Article ID:51436,15 pages
10.4236/ojfd.2014.44026
A Seven-Dimensional System of the Navier-Stokes Equations for a Two-Dimensional Incompressible Fluid on a Torus
Heyuan Wang1, Yan Gao2
1College of Sciences, Liaoning University of technology, Jinzhou, China
2Liaoning Petro-chemical Vocational Technology College, Jinzhou, China
Email: wangheyuan6400@sina.com, gaoyan67830@126.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 August 2014; revised 29 September 2014; accepted 30 October 2014
ABSTRACT
A seven-mode truncation system of the Navier-Stokes equations for a two-dimensional incompressible fluid on a torus is considered. Its stationary solutions and stability are presented; the existence of the attractor and the global stability of the system are discussed. The whole process, which shows a chaos behavior approached through instability of invariant tori, is simulated numerically by computers with the changing of Reynolds number. Based on numerical simulation results of bifurcation diagram, Lyapunov exponent spectrum, Poincare section, power spectrum and return map of the system, some basic dynamical behaviors of the new chaos system are revealed.
Keywords:
The Navier-Stokes Equations, Strange Attractor, Lyapunov Function, Bifurcation, Chaos

1. Introduction
In recent years much attention has been devoted to the study of simple differential or difference equations, which although deterministic, exhibit a transition as some parameters go through certain values to a chaos behavior. The equations which are studied often arise in a natural way as simplified models in fluid dynamics and in ecology. The best known examples are perhaps the models of [1] -[3] . In these models a chaos behavior arises as a consequence of the appearance of an attractor of complicated structure which is called “strange attractor”. Trajectories in a neighborhood of the attractor appear to move in a completely erratic way. Phenomena of this kind are predicted under certain hypothesis, by the mathematical theory of turbulence of Ruelle and Takens [4] . In the following we consider a model obtained by a suitable seven-mode truncation of the Navier-Stokes equations for a 2-dimensional incompressible fluid on a torus [5] . The paper [5] has been published in Proceedings of the IWCFTA 2012, but the published paper is too rough and several deficiencies in the study of the published paper can be found. Only local results of dynamic behavior are given, and some simulation results are wrong; the transition to chaos is confused. This paper gives more accurate simulation results, discusses the dynamic behavior of the system at the high values of the Reynolds number, and analyses the evolution of the dynamic behavior of the system. This paper is extension and modification of the published article [5] and the content is more abundant. We argue on the basis of numerical simulation results analysis where in a certain range of the Reynolds number our system behaves in a way similar to that predicted by Ruelle and Takens. Dynamical behaviors of this new chaotic system, including some basic dynamical properties, bifurcations and routes to chaos, etc., have been investigated both theoretically and numerically by changing Reynolds number. Our purpose is to study how the phenomena of the model change when the number of modes in the truncation is slightly increased. The existence of the attractor and the global stability of the equations have been firmly verified and these theories can be used in other similar systems. Furthermore, some basic dynamical behaviors of the new chaos system, such as bifurcation diagram, Lyapunov exponent spectrum, Poincare section, power spectrum and return map, are presented.
2. Seven-Mode Lorenz-Like Equations
Consider the incompressible Navier-Stokes equations:
 (1)
(1)
 (2)
(2)
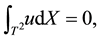 (3)
(3)
on the torus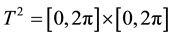 , where
, where  is the velocity field,
is the velocity field,  is the pressure and
is the pressure and 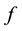 is a (periodic) volume force.
is a (periodic) volume force.
We expanded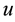 ,
, 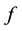 ,
, 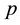 in Frourier series:
in Frourier series:
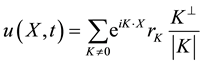 (4)
(4)
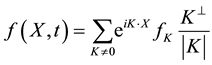 (5)
(5)
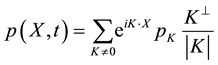 (6)
(6)
where  is a “wave vector”, with integer components,
is a “wave vector”, with integer components, 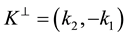 ,
,  is a function of
is a function of


where 


We take as the set of vectors 








Taking the force acting on the mode

of Calculation we obtain the following system

3. The Stationary Solution and Their Stability Properties
In this section we discuss the stationary solution and their stability properties of the system (2.8). Let
setting 
(a) For 

stable for 
(b) For 


where

(c) For
4. The Existence of Attractor and Analysis of Global Stability
In the following we prove the existence of attractor of the system (8).
By calculating 
accordingly,
letting
as a result,
, then
From above we have
If 

When the system is a global stability,its orbits contract into a domain called the trapping region. Therefore, if the existence of the trapping region is proved, the system has the global stability, though the stationary solutions are unstable. We construct a following Liapunov function of the system (8)

Setting



Obviously 









From the Liapunov theory we know that the orbits out of system (8) will enter E. Namely E is the trapping region of the Equations (8). Though the stationary solutions 
5. Numerical Simulation
With the increasing of Reynolds number
1) At 

2) When






3) At




Figure 1. (P± is stable for r < 114.685).
Figure 2. (P± is stable for r < 114.685).
Figure 3. (P± is stable for r < 114.685).
Figure 4. (P± is stable for r < 114.685).
Figure 5. (Periodic orbit for r = 114.685).
Figure 6. (Periodic orbit for r = 114.685).
Figure 7. (The attracting tori for r = 143.463).
Figure 8. (The attracting tori for r = 143.463).
4) With the increasing of the Reynolds number r, a strong hysteresis phenomenon(i.e., coexistence of stable attractors) appears, in some intervals hysteresis takes place between closed orbits and tori (Figures 9-19).
5) At
6) Figure 26 and Figure 27 show Bifurcation diagrams and the largest Lyapunov exponents of the system (2.8).
7) Figures 28-30 show Poincare section, return map and power spectrum of the system (2.8) when
8) For 

6. Conclusions
In this work we have reported the results of our theoretical and numerical investigation on a model of seven nonlinear ordinary differential equations. Such a model, obtained by a suitable seven-mode truncation of the Navier-Stokes equations for an incompressible fluid on a torus, exhibits a very varied phenomenology, with an
Figure 9. (Quasi-periodic orbit for r = 148.685).
Figure 10. (Quasi-periodic orbit for r = 148.685).
Figure 11. (Quasi-periodic orbit for r = 149.35).
Figure 12. (Quasi-periodic orbit for r = 151.35).
Figure 13. (Quasi-periodic orbit for r = 152.65).
Figure 14. (Quasi-periodic orbit for r = 154.35).
Figure 15. (Quasi-periodic orbit for r = 155.12).
Figure 16. (Quasi-periodic orbit for r = 156.43).
Figure 17. (The attracting tori for r = 156.43).
Figure 18. (Quasi-periodic orbit for r = 156.83).
Figure 19. (The attracting tori for r = 157.23).
Figure 20. (The strange attractor for r = 158.5).
Figure 21. (The strange attractor for r = 159.5).
Figure 22. (The strange attractor for r = 159.5).
Figure 23. (The strange attractor for r = 160.5).
Figure 24. (The strange attractor for r = 250.5).
Figure 25. (The strange attractor for r = 360.5).
Figure 26. (Bifurcation diagrams).
Figure 27. (The largest Lyapunov exponents).
Figure 28. (The Poincare section for r = 184).
Figure 29. (The return map for r = 184).
Figure 30. (The power spectrum for r = 184).
interesting sequence of bifurcations. From numerical results we present four different and independent stories describing the complete phenomenology of the model. The first story consists of a sequence of a bifurcations very similar to the one found by Curry in [4] : The fixed point 







For all the values of the Reynolds number r larger than 158.631, when no stable periodic orbits or tori are present any more, the model exhibits a turbulent behavior. In fact any randomly chosen point describes trajectories which appear to be completely random and sensitively dependent on initial conditions. Since all the numerical investigations carried up to 

Acknowledgements
We thank the editor and the referee for their comments. Research work is funded by the funds for education department of Liaoning Province (L2013248) and science and technology funds of Jinzhou city (13A1D32).
References
- Wang, H.Y. (2012) Dynamical Behaviors and Numerical Simulation of Lorenz Systems for the Incompressible Flow between Two Concentric Rotating Cylinders. International Journal of Bifurscation and Chaos, 22, 1-11.
- Wang, H.Y. and Jiang, H.B. (2007) Bifurcation Analysis of the Model System Similar to the Lorenz Equations of the Flow between Two Concentric Rotating Spheres. Numerical Mathematics: A Journal of Chinese Universities English Series, 29, 278-288.
- Franceschini, V. and Zanasi, R. (1992) Three-Dimensional Navier-Stokes Equations Truncated on a Torus. Nonlinearity, 4, 189-209. http://dx.doi.org/10.1088/0951-7715/5/1/008
- Curry, J.H. (1978) A Generalized Lorenz System. Communications in Mathematical Physics, 60, 193-204. http://dx.doi.org/10.1007/BF01612888
- Wang, H.Y. and Gao, Y. (2012) The Dynamical Behaviors and Numerical Simulation of a Seven-Mode Truncation System of the Navier-Stokes Equations for a Two-Dimensional Incompressible Fluid on a Torus. Proceedings of the IWCFTA 2012, 54-57.
- Ladyzhenskaya, O.A. (1969) The Mathematical Theory of Viscous Incompressible Flows. Gordon and Breach, New York.
- Li, K.T. and Ma, Y.C. (1992) The Hilbert Space Method of Math and Physics Equations. Xi’an Jiaotong University Press, Xi’an. (In Chinese)
- Liu, B.Z. and Peng, J.H. (2004) Nolinear Dynamic. Higher Education Publishing House, Beijing. (In Chinese)









































