Open Journal of Fluid Dynamics
Vol.04 No.02(2014), Article ID:45653,4 pages
10.4236/ojfd.2014.42009
Analysis of the Force Acting on the Sucker Rod by Polymer Solution
Lili Liu1, Shuren Yang1, Lihui Wang2, Di Xu1, Liang Zhao3, Yue Cui1
1Department of Petroleum Engineering, Northeast Petroleum University, Daqing, China
2Daqing Petroleum Equipment Group, Daqing, China
3Daqing Oilfield Tianyu Engineering Design Co., Ltd., Daqing, China
Email: dqliull2009@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 March 2014; revised 12 April 2014; accepted 19 April 2014
ABSTRACT
With selecting lower-convected Maxwell constitutive equation, polymer solution flow equation in eccentric annulus is established. And the distribution rule of the force acting on the sucker rod by polymer solution has been gained. The result shows the eccentric ratio and the movement velocity of the sucker rod are major influence factors on the radial force. The greater the ratio is, the greater the force of sucker rod is. Then the eccentric wear is easier to appear.
Keywords:
Viscous-Elastic Fluids, Eccentric Annulus, Normal Stress, Radial Force, Eccentric Wear

1. Introduction
With the development of the enhanced oil recovery technology, Polymer flooding has been widely used. But because of the viscous-elasticity of polyer flooding produced fluid, there would be a radial force acting on the sucker rod, which was vertical to axis. The combination of radial force, inertial force and resistance makes sucker rod bent. Thus, the phenomenon of eccentric wear will be heavier and rupture of sucker rod will always happen, which has become the major problem in Polymer flooding Wells production. So, it has practical significance to carry out the study of viscous-elastic fluid in eccentric annulus.
Before there is few study about radial force due to the viscous-elasticity of polymer flooding produced fluid. In this article, on the base of the steady flow velocity profile in the viscous-elastic fluid in eccentric annulus with the internal rod moving axially, the lower-convected Maxwell constitutive equation model is used, the stress distribution of the flow field and the radial force acting on the sucker rod are calculated, the influence factors of radial force and eccentric wear of sucker rod are analyzed, which provides theoretical basis for the prevention of eccentric wear.
2. Velocity Profile
The velocity of eccentric annulus flow of viscous-elastic fluid can be solved by using control volume method and the ADI method [1] [2] . The U/Umax contour of flow field is shown in Figure 1. Solving the velocity field is the basis for further calculating stress field and sucker rod stress. Before solving the stress distribution of the flow field, selecting the appropriate constitutive equations should be the first.
3. Normal Stress and the Constitutive Equation
The lower-convected Maxwell constitutive equation [3] of the viscous-elastic fluid is
 (1)
(1)
where: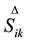 ―the derivative of stress component lower-convected.
―the derivative of stress component lower-convected.
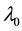 ―relaxation time.
―relaxation time.
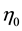 ―viscosity.
―viscosity.
Under the condition of flowing in the paper, each component of the lower-convected Maxwell constitutive equation in the bipolar reference frame can be expressed as:
 (2)
(2)
 (3)
(3)
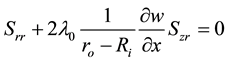 (4)
(4)
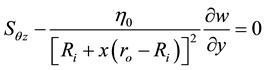 (5)
(5)
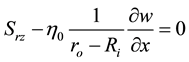 (6)
(6)
 (7)
(7)
Figure 1. Flow field velocity distribution isolines.
After the velocity distribution of flow field is got, the deformation rate distribution and the Ericksen tensor of flow field can be calculated further. And then the stress distribution of the flow field can be calculated by using the constitution equation. The normal stress Srr acting on the inner tube in the flow field is the most interested. For the resultant force is the major factor of sucker rod eccentric wear. The normal stress on the surface of the inner tube can be expressed as
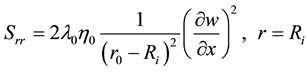 (8)
(8)
The unit length rod radial force F can be calculated by integrating Srr along the inner tube by angle, namely
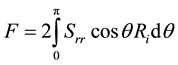 (9)
(9)
Because the flow field is symmetrical when the sucker rod and tubing is concentric (Namely the various angles of normal stress is equal), the resultant force is zero. But, in the engineering practice, it is difficult to guarantee the sucker rod and tubing concentric, velocity field is asymmetric and the normal stress field is asymmetric, too. Then the resultant force F of the normal stress is no longer zero.
4. The Calculation Results and Analysis
In engineering practice, the flow in the wellbore is combined by the flow produced by the pressure gradient and the flow produced by sucker rod. The velocity distribution curves of the sucker rod at the certain speed U of down run and up run are shown in Figure 2 and Figure 3.
Figure 2(c) and Figure 3(c) show that the velocity gradient of narrow gap is always greater than that of the wide gap. Therefore, no matter sucker rod is downward or upward, the velocity of narrow gap is always greater than that of the wide gap. And because the normal stress and the square of the velocity gradient are proportional, so the normal stress of narrow gap is greater than that of the wide gap. But the normal stress acting on the sucker rod is tensile stress, so the resultant force F must point to narrow gap, and the radial force will also make the inner tube eccentricity greater. (Normal stress distribution on the surface of the inner tube is shown in Figure 4). This conclusion and the experimental observation are completely consistent. Compared with the sucker rod down run, the width and narrow side velocity gradient of the sucker rod up run is reduced. Then the normal stress difference is smaller and the radial force is less than the down run slightly. This conclusion is also proved fully by the phenomenon of the experiment. The eccentricity determines the asymmetric degree of the flow field directly, and then determines the resultant force of the normal stress―the radial force. The bigger the eccentricity is, the stronger the asymmetry is. And the normal force of the sucker rod is greater. The relationship between the radial force and the eccentricity of the sucker rod per meter is shown in Figure 5.
5. Conclusion
The major factors of the radial force in the sucker rod are the eccentricity and its velocity. The greater the ec-

Figure 2. The velocity distribution of sucker rod down run in the wellbore. (a) The velocity distribution when the sucker rod is rest; (b) The velocity distribution when the sucker rod moves; (c) The velocity distribution when the sucker rod moves and the fluid flows at the same time.

Figure 3. The velocity distribution of sucker rod up run in the wellbore. (a) The velocity distribution when the sucker rod is rest; (b) The velocity distribution when the sucker rod moves; (c) The velocity distribution when the sucker rod moves and the fluid flows at the same time.
Figure 4. Normal stress Srr distribution on the surface of the inner tube.

Figure 5. The relationship between the radial force and the eccentricity.
centricity is, the bigger the radial force is, so the velocity of the sucker rod is, which provides theoretical basis for the further analysis of the cause of the sucker rod eccentric wear and the method of preventing eccentric wear.
References
- Patankar, S.V. (1983) The Numerical Calculation of Heat Transfer and Fluid Flow. Zhang Zheng Translation, Science Press, Beijing, 131-148.
- Yang, S.R. (1997) Velocity Profile of Axial-Laminar Flow for Power-Law Fluids through Eccentric Annuli. Daqing Petroleum Institute, 3, 122-124.
- Han, S.F. (2000) Non-Newtonian Fluid Constitutive Equation and Calculative Analytic Theory. Science Press, Beijing, 145-162.



