Open Journal of Fluid Dynamics
Vol.4 No.1(2014), Article ID:43395,14 pages DOI:10.4236/ojfd.2014.41001
Combined Effects of Centrifugal and Coriolis Instability of the Flow through a Rotating Curved Duct with Rectangular Cross Section
Rabindra Nath Mondal1, Samir Chandra Ray2, Shinichiro Yanase3
1Department of Mathematics, Jagannath University, Dhaka, Bangladesh
2Department of Mathematics, Bangabandhu Sheikh Mujibur Rahman Science and Technology University, Gopalganj, Bangladesh
3Department of Mechanical and System Engineering, Faculty of Engineering, Okayama University, Okayama, Japan
Email: rnmondal71@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 14 November 2013; revised 14 December 2013; accepted 23 December 2013
ABSTRACT
Combined effects of centrifugal and coriolis instability of the flow through a rotating curved duct with rectangular cross section have been studied numerically by using a spectral method, and covering a wide range of the Taylor number 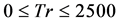 for a constant Dean number
for a constant Dean number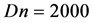 . The rotation of the duct about the center of curvature is imposed in the positive direction, and the effects of rotation (Coriolis force) on the flow characteristics are investigated. As a result, multiple branches of asymmetric steady solutions with two-, threeand multi-vortex solutions are obtained. To investigate the non-linear behavior of the unsteady solutions, time evolution calculations as well as power spectrum of the unsteady solutions are performed, and it is found that the unsteady flow undergoes through various flow instabilities in the scenario “chaotic ( multi-periodic ( periodic ( steady-state”, if Tr is increased in the positive direction. The present results show the characteristics of both the secondary flow and axial flow distribution in the flow.
. The rotation of the duct about the center of curvature is imposed in the positive direction, and the effects of rotation (Coriolis force) on the flow characteristics are investigated. As a result, multiple branches of asymmetric steady solutions with two-, threeand multi-vortex solutions are obtained. To investigate the non-linear behavior of the unsteady solutions, time evolution calculations as well as power spectrum of the unsteady solutions are performed, and it is found that the unsteady flow undergoes through various flow instabilities in the scenario “chaotic ( multi-periodic ( periodic ( steady-state”, if Tr is increased in the positive direction. The present results show the characteristics of both the secondary flow and axial flow distribution in the flow.
Keywords:
Rotating Curved Duct; Dean Number; Taylor Number; Secondary Flow; Periodic Solution

1. Introduction
Recently, great attention has been paid for the study of flows and heat transfer through rotating curved ducts and channels because of its practical application in chemical, mechanical, bio-mechanical and biological engineering. A quantitative analogy between flows in stationary curved pipes and orthogonally rotating straight pipes has been reported by Ishigaki [1] [2] . Taking this analogy as a basis, this study describes the characteristics of more general and complicated flow in rotating curved ducts. Such rotating flow passages are used in cooling systems in rotating machinery such as in gas turbines, turbo-machinery, electric generators and electric motors. The readers can refer to Berger et al. [3] and Nandakumar and Masliyah [4] for some outstanding reviews on curved duct flows.
One of the interesting phenomena of the flow through a curved duct is the bifurcation of the flow because generally there exist many steady solutions due to channel curvature. An early complete bifurcation study of two-dimensional (2-D) flow through a curved duct with square cross section was performed by Winters [5] . However, an extensive treatment of the flow through a curved square duct was reported by Mondal et al. [6] . He found a close relationship between the unsteady solutions and the bifurcation diagram of steady solutions. Ishigaki [2] examined the flow structure and friction factor numerically for both the counter-rotating and co-rotating curved circular pipe with a small curvature. Selmi et al. [7] examined the combined effects of system rotation and curvature on the bifurcation structure of two-dimensional flows in a rotating curved square duct. Selmi and Nandakumer [8] performed studies on the flow in rotating curved rectangular ducts. Yamamoto et al. [9] employed spectral method to examine the flow structure and the flow rate ratio in a rotating curved square duct flow and found six-cell phenomenon of the secondary flow. Recently, Mondal et al. [10] performed a comprehensive numerical study on the bifurcation structure and the stability of solutions for laminar forced convection in a rotating curved duct of square cross section, and revealed some new features on fluid flow. However, the complete flow structures under the combined action of coriolis and centrifugal instability are still unrevealed for the rotating curved rectangular duct flow at high rotation. It is an attempt of the present study.
It is well known that, fluid flowing in a rotating curved duct is subjected to two forces: the Coriolis force, caused by the rotation of the duct, and centrifugal force caused by the curvature of the duct. These two forces affect each other, as a result complex behavior of the secondary flow and the axial flow can be obtained (Wang and Cheng [11] ). For isothermal flows of a constant property fluid, however, the Coriolis force tends to produce vorticity while centrifugal force is purely hydrostatic (Zhang et al. [12] ). When a temperature induced variation of fluid density occurs for non-isothermal flows, both Coriolis and centrifugal type buoyancy forces can contribute to the generation of vorticity (Mondal et. al., [13] ). These two effects of rotation either enhance or counteract each other in a non-linear manner depending on the direction of wall heat flux and the flow domain. Therefore, the effect of rotation of the system is more subtle and complicated and yields new; richer features of flow and heat transfer in general, bifurcation and stability in particular, for non-isothermal flows. Mondal et al. [13] ] performed numerical prediction of the non-isothermal flows through a rotating curved square duct and revealed some of such new features. Very recently, Mondal et al. [14] investigated the combined effects of the Coriolis force and the centrifugal force on the flows in a rotating curved square duct numerically. The secondary flow characteristics in a curved square duct were investigated experimentally by using visualization method by Yamamoto et al. [15] . Three-dimensional incompressible viscous flow and heat transfer in a rotating U-shaped square duct were studied numerically by Nobari et al. [16] . However, there is no known study on bifurcation and unsteady flow characteristics in a rotating curved rectangular duct with large rotational speed. The present paper is, therefore, an attempt to fill up this gap.
Time dependent analysis of fully developed curved duct flows was first initiated by Yanase and Nishiyama [17] for a rectangular cross section. In that study, they investigated unsteady solutions for the case where dual solutions exist. However, time-dependent behavior of the flow in a curved rectangular duct over a wide range of aspect ratios was investigated, in detail, by Yanase et al. [18] numerically. They observed that periodic oscillations are available with symmetry condition while aperiodic time evolutions without symmetric condition. Wang and Yang [19] [20] performed numerical as well as experimental investigation on fully developed periodic oscillation in a curved square duct. Flow visualization in the range of Dean numbers from 50 to 500 was carried out in their experiment. They showed, both experimentally and numerically, that the temporal oscillation takes place between symmetric/asymmetric 2-cell and 4-cell flows where there are no stable steady flows. Applying spectral method, Yanase et al. [21] performed comprehensive numerical study of the time-dependent solutions for the non-isothermal flows through a curved rectangular duct, and studied the effects of secondary flows on convective heat transfer. In order to study the time-dependent behavior of the unsteady solutions, recently, Mondal et al. [22] performed numerical prediction of the unsteady solutions through curved square duct for isothermal flow. They showed that periodic solutions turn into chaotic solution through a multi-periodic solution, if the Dean number is increased no matter what the curvature is. However, transient behavior of the unsteady solutions, such as periodic, multi-periodic or chaotic solutions, is yet unresolved for the flow through a rotating curved rectangular duct at large pressure gradient with large rotational speed. This motivated the present study to investigate the non-linear behavior of the unsteady solutions by time-evolution calculation.
In the present study, a comprehensive numerical result is presented for fully developed bifurcation structure of two-dimensional (2D) viscous incompressible fluid flow through a rotating curved rectangular duct. Flow characteristics are investigated over a wide range of Taylor number 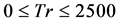 for the Dean number Dn = 2000. Studying the effects of rotation on the flow characteristics, caused by the combined action of centrifugal force and Coriolis force, is an important objective of the present study.
for the Dean number Dn = 2000. Studying the effects of rotation on the flow characteristics, caused by the combined action of centrifugal force and Coriolis force, is an important objective of the present study.
2. Governing Equations
Consider that the flow is viscous and incompressible which is streaming through a rotating curved duct with rectangular cross section. Let 2h and 2l be the height and the width of the cross section. Figure 1 shows the coordinate system, where C is the center of the duct crosssection and L is the radius of curvature of the duct. The 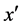 and
and  axes are taken to be in the horizontal and vertical directions respectively, and
axes are taken to be in the horizontal and vertical directions respectively, and 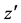 is the coordinate along the center-line of the duct, i.e., the axial direction. The system rotates at a constant angular velocity
is the coordinate along the center-line of the duct, i.e., the axial direction. The system rotates at a constant angular velocity  around the
around the 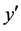 axis. It is assumed that the flow is uniform in the axial direction, and that it is driven by a constant pressure gradient
axis. It is assumed that the flow is uniform in the axial direction, and that it is driven by a constant pressure gradient 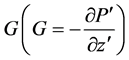 along the center-line of the duct, i.e. the main flow direction. Then the continuity equation and the Navier-Stokes equation, in terms of dimensional variables, are expressed as Continuity equation
along the center-line of the duct, i.e. the main flow direction. Then the continuity equation and the Navier-Stokes equation, in terms of dimensional variables, are expressed as Continuity equation
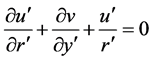 (1)
(1)
Momentum equations
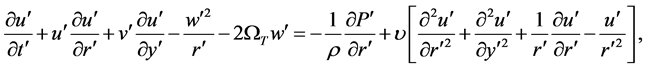 (2)
(2)
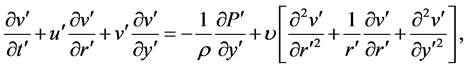 (3)
(3)
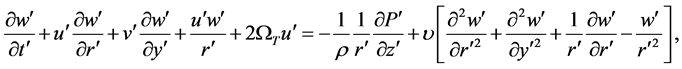 (4)
(4)
where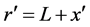 , and
, and 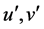 and
and 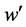 are the dimensional velocity components in the
are the dimensional velocity components in the  and
and 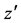 directions respectively. In Equations (1) to (4) the variables with prime denote the dimensional quantities. To nondimensionalize the equations, we use the non-dimensional variables defined as
directions respectively. In Equations (1) to (4) the variables with prime denote the dimensional quantities. To nondimensionalize the equations, we use the non-dimensional variables defined as
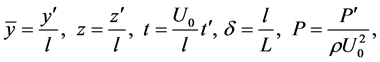

where 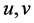 and
and  are the non-dimensional velocity components in the
are the non-dimensional velocity components in the 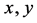 and
and 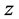 directions, respectively; t is the non-dimensional time, P is the non-dimensional pressure,
directions, respectively; t is the non-dimensional time, P is the non-dimensional pressure,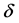 is the non-dimensional curvature defined as
is the non-dimensional curvature defined as
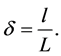 The sectional stream function
The sectional stream function 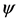 is introduced as
is introduced as
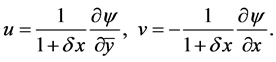 (5)
(5)
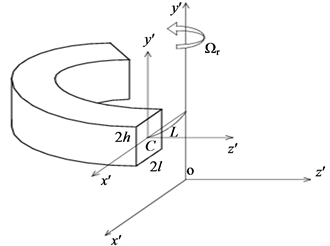
Figure 1. Rotating coordinate system.
Then, the basic equations for  and
and 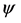 are expressed in terms of non-dimensional variables as
are expressed in terms of non-dimensional variables as
 (6)
(6)
 (7)
(7)
where,
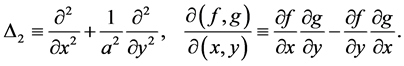 (8)
(8)
The non-dimensional parameters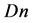 , the Dean number and
, the Dean number and , the Taylor number which appear in Equations (6) and (7) are defined as:
, the Taylor number which appear in Equations (6) and (7) are defined as:
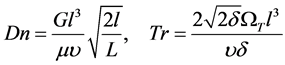 (9)
(9)
In the present study,  varies while Dn,
varies while Dn, 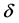 ,
, 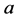 and
and 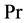 are fixed as Dn = 2000,
are fixed as Dn = 2000, 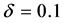 ,
,  and
and 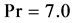 (water). The rigid boundary conditions for
(water). The rigid boundary conditions for 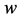 and
and  are used as
are used as
 (10)
(10)
3. Numerical Calculations
In order to solve Equations (6) to (7) numerically, the spectral method is used (Gottlieb and Orazag [23] ). By this method the variables are expanded by using the expansion functions  and
and 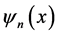 as
as
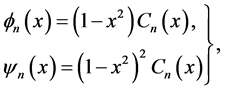 (11)
(11)
where 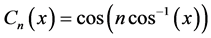 is the
is the  order Chebyshev polynomial.
order Chebyshev polynomial.  and
and 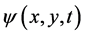 are expanded in terms of the expansion functions
are expanded in terms of the expansion functions 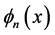 and
and 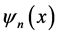 as
as
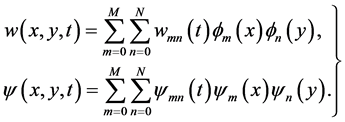 (12)
(12)
First, steady solutions are obtained by the Newton-Rapshon iteration method. Then, in order to calculate the unsteady solutions, the Crank-Nicolson and Adams-Bash-forth methods together with the function expansion (12) and the collocation methods are applied.
4. Flux through the Duct
The dimensional total flux 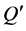 through the duct in the rotating coordinate system is calculated by:
through the duct in the rotating coordinate system is calculated by:
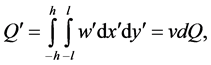 (13)
(13)
where
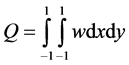 (14)
(14)
is the dimensionless total flux. The mean axial velocity, 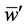 is expressed as
is expressed as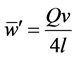 . In the present study, Q is used to denote the steady solution branches and to pursue time evolution of the unsteady solutions.
. In the present study, Q is used to denote the steady solution branches and to pursue time evolution of the unsteady solutions.
5. Results and Discussion
5.1. Steady Solutions and Flow Patterns
We obtained four branches of symmetric/asymmetric steady solutions for the Dean number  over the Taylor number
over the Taylor number 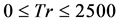 , as shown in Figure 2. The four steady solution branches are named the first steady solution branch (first branch, thick solid line), the second steady solution branch (second branch, thin solid line), the third steady solution branch (third branch, thick dotted line) and the fourth steady solution branch (fourth branch, long dash line), respectively. The steady solution branches are obtained by the path continuation technique (Keller [24] ) with various initial guesses as discussed by Mondal [25] . In this regard, it should be noted that Mondal et al. [13] also obtained four braches of steady solutions for the non-isothermal flow through a rotating curved square duct.
, as shown in Figure 2. The four steady solution branches are named the first steady solution branch (first branch, thick solid line), the second steady solution branch (second branch, thin solid line), the third steady solution branch (third branch, thick dotted line) and the fourth steady solution branch (fourth branch, long dash line), respectively. The steady solution branches are obtained by the path continuation technique (Keller [24] ) with various initial guesses as discussed by Mondal [25] . In this regard, it should be noted that Mondal et al. [13] also obtained four braches of steady solutions for the non-isothermal flow through a rotating curved square duct.
Then, we obtained secondary vortices on various branches of steady solutions, and it is found that at the same value of Tr sometimes we obtain two-vortex solution, while sometimes twoand multi-vortex solutions. It is found that the first and fourth steady solution branche consists of symmetric solutions while the second and third branches asymmetric solutions. The first branch consists of symmetric two-, four-, six-, eightand ten-vortex solutions, the second branch is composed of asymmetric twoand four-vortex solutions, the third branch is characterized by asymmetric twoand four-vortex solutions, while the fourth branch is comprised with asymmetric twoto ten-vortex solutions. These vortices are generated due to the combined action of the centrifugal force and Coriolis force. The steady solution branches as well as the formation of secondary vortices on various branches are not shown here for brevity; however, we show some contours of secondary flow patterns and axial flow distribution at some specific values of Tr. To observe the pattern variation and development of the secondary vortices, also called the Dean vortices, contours of secondary flow patterns are shown in Figure 3 at various values of Tr for Dn = 2000. In the figures of the secondary flow, solid lines 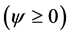 show that the secondary flow is in the counter clockwise direction while the dotted lines
show that the secondary flow is in the counter clockwise direction while the dotted lines 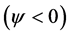 in the clockwise direction. As seen in Figure 3, the secondary flow is two-, four-, six-, eightand ten-vortex solutions, which are obtained on different branches of steady solutions. Figure 4 shows typical contours of secondary flow patterns and axial flow distribution on the steady solution branch at
in the clockwise direction. As seen in Figure 3, the secondary flow is two-, four-, six-, eightand ten-vortex solutions, which are obtained on different branches of steady solutions. Figure 4 shows typical contours of secondary flow patterns and axial flow distribution on the steady solution branch at 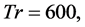 where it is found that the secondary flow consists of symmetric and asymmetric twoto ten-vortex solutions at
where it is found that the secondary flow consists of symmetric and asymmetric twoto ten-vortex solutions at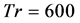 .
.
5.2. Unsteady Solutions
In order to investigate the non-linear behavior of the unsteady solutions, time-evolution calculations of the unsteady solutions are performed for 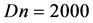 over the Taylor number
over the Taylor number 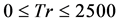 . Time evolution of
. Time evolution of 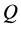 for
for 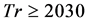 shows that the value of
shows that the value of 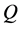 quickly approaches steady-state solution no matter what the initial condition we use. Then, in order to see the unsteady flow characteristics for Tr < 2030 and Tr > 2030, time
quickly approaches steady-state solution no matter what the initial condition we use. Then, in order to see the unsteady flow characteristics for Tr < 2030 and Tr > 2030, time
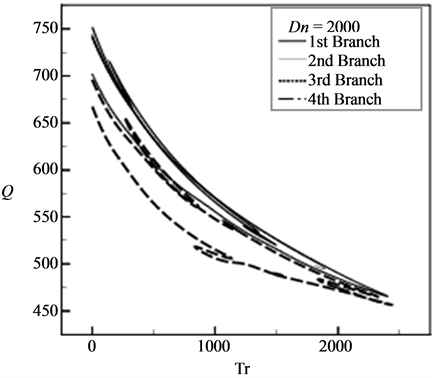
Figure 2. Solution structure of the steady solutions for 0 ≤ Tr ≤ 2500 at Dn = 2000.

Figure 3. Streamlines of secondary flow (top) and axial flow (bottom) on the steady solution branches at various values of Tr.
evolutions of 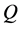 are then performed for
are then performed for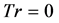 , 500, 1000, 1500, 1870, 1880, 1900, 1950 and 2050. Figure 5(a) shows time-evolution of
, 500, 1000, 1500, 1870, 1880, 1900, 1950 and 2050. Figure 5(a) shows time-evolution of 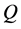 for
for  at Dn = 2000, where it is seen that the flow oscillates irregularly, i.e. the flow is chaotic. This chaotic oscillation is well justified by drawing the power spectrum as shown in Figure 5(b), where it is seen that lots of continuous line spectra with different frequencies are available, which suggests that the unsteady flow at
at Dn = 2000, where it is seen that the flow oscillates irregularly, i.e. the flow is chaotic. This chaotic oscillation is well justified by drawing the power spectrum as shown in Figure 5(b), where it is seen that lots of continuous line spectra with different frequencies are available, which suggests that the unsteady flow at  is chaotic. Typical contours of secondary flow patterns and axial flow distribution at
is chaotic. Typical contours of secondary flow patterns and axial flow distribution at  are shown in Figure 5(c), where it is seen that the flow oscillates between asymmetric sixto eight-vortex solutions. Time-evolution of Q for
are shown in Figure 5(c), where it is seen that the flow oscillates between asymmetric sixto eight-vortex solutions. Time-evolution of Q for 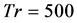 is shown in Figure 6(a), where it is seen that the
is shown in Figure 6(a), where it is seen that the
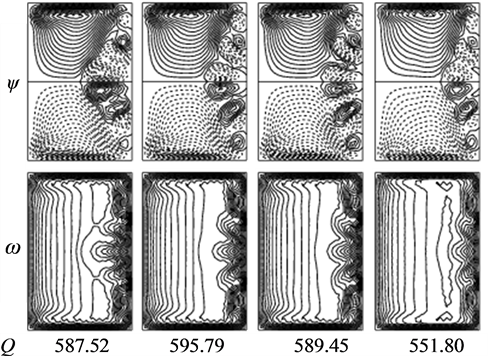
Figure 4. Streamlines of secondary flow (top) and axial flow (bottom) on the fourth steady solution branch for various values of Q at Tr = 600
flow is also chaotic. Power spectrum of the time change of 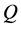 for
for 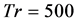 is shown in Figure 6(b), which justifies the chaotic behavior of the unsteady solution at Tr = 500. Typical contours of secondary flow patterns and axial flow distribution for
is shown in Figure 6(b), which justifies the chaotic behavior of the unsteady solution at Tr = 500. Typical contours of secondary flow patterns and axial flow distribution for 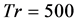 are shown in Figure 6(c), where it is seen that the flow oscillates between asymmetric sixto eight-vortex solutions.
are shown in Figure 6(c), where it is seen that the flow oscillates between asymmetric sixto eight-vortex solutions.
Then we performed time-evolutions of 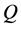 for
for  and 2000. The results are shown in Figures 7(a) and 8(a) respectively. It is found that the unsteady flow further oscillates irregularly, i.e. chaotic. In order to see the mode of the chaotic oscillations, we then performed power spectra of the time change of
and 2000. The results are shown in Figures 7(a) and 8(a) respectively. It is found that the unsteady flow further oscillates irregularly, i.e. chaotic. In order to see the mode of the chaotic oscillations, we then performed power spectra of the time change of 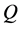 as shown in
as shown in
Figures 7(b) and 8(b) for 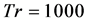 and Tr = 1500 respectively, where lots of continuous line spectra with different frequencies are seen, which suggests that the unsteady flow at
and Tr = 1500 respectively, where lots of continuous line spectra with different frequencies are seen, which suggests that the unsteady flow at  and Tr = 1500 are chaotic. Typical contours of secondary flow patterns and axial flow distribution for
and Tr = 1500 are chaotic. Typical contours of secondary flow patterns and axial flow distribution for  and Tr = 1500 are shown in Figures 7(c) and 8(c) respectively, where it is seen that the flow oscillates between asymmetric fourto ten-vortex solutions. Figure 9(a) shows time-evolution of
and Tr = 1500 are shown in Figures 7(c) and 8(c) respectively, where it is seen that the flow oscillates between asymmetric fourto ten-vortex solutions. Figure 9(a) shows time-evolution of 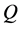 for
for 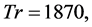 where it is seen that the flow is chaotic. This chaotic solution is well justified by the power spectrum of the time change of
where it is seen that the flow is chaotic. This chaotic solution is well justified by the power spectrum of the time change of 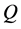 as shown in Figure 9(b), where it is seen that lots of continuous line spectra with different frequencies are available, which suggests that the flow is chaotic. Secondary flow patterns and axial flow distribution for
as shown in Figure 9(b), where it is seen that lots of continuous line spectra with different frequencies are available, which suggests that the flow is chaotic. Secondary flow patterns and axial flow distribution for 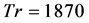 are shown in Figure 9(c), where it is seen that the flow oscillates between asymmetric sixand eight-vortex solutions.
are shown in Figure 9(c), where it is seen that the flow oscillates between asymmetric sixand eight-vortex solutions.
Then we performed time evolution of Q for 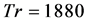 as shown in Figure 10(a). As seen in Figure 10(a), the time-dependent solution for
as shown in Figure 10(a). As seen in Figure 10(a), the time-dependent solution for 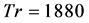 is multi-periodic. Power spectrum of the time change of
is multi-periodic. Power spectrum of the time change of 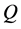 for Tr = 1880 is also shown in Figure 10(b), in which not only the line spectrum of the fundamental frequency and its harmonics but also other line spectrum and their harmonics are seen, which suggests that the flow is multi-periodic. Secondary flow patterns and axial flow distributions are shown in Figure 10(c), for one period of oscillation at 5.7 ≤ t ≤ 5.91 where it is seen that the unsteady flow at
for Tr = 1880 is also shown in Figure 10(b), in which not only the line spectrum of the fundamental frequency and its harmonics but also other line spectrum and their harmonics are seen, which suggests that the flow is multi-periodic. Secondary flow patterns and axial flow distributions are shown in Figure 10(c), for one period of oscillation at 5.7 ≤ t ≤ 5.91 where it is seen that the unsteady flow at 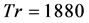 oscillates between asymmetric fourand six-vortex solutions.
oscillates between asymmetric fourand six-vortex solutions.
Next, time evolution of Q for 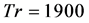 is shown in Figure 11(a), where it is seen that the flow oscillates periodically. It is justified by the power spectrum as shown in Figure 11(b), where the fundamental frequency and its harmonics as well as line spectra with small frequency is seen, which indicates that the oscillation presented in Figure 11(b) is multi-periodic, but not periodic. It is seen that the fundamental mode is higher than that of the other modes, which clearly suggests that the flow at Tr = 1900 is perfectly multi-periodic. Contours of secondary flow patterns and axial flow distributions are shown in Figure 11(c). As seen in Figure 11(c), the unsteady solution at
is shown in Figure 11(a), where it is seen that the flow oscillates periodically. It is justified by the power spectrum as shown in Figure 11(b), where the fundamental frequency and its harmonics as well as line spectra with small frequency is seen, which indicates that the oscillation presented in Figure 11(b) is multi-periodic, but not periodic. It is seen that the fundamental mode is higher than that of the other modes, which clearly suggests that the flow at Tr = 1900 is perfectly multi-periodic. Contours of secondary flow patterns and axial flow distributions are shown in Figure 11(c). As seen in Figure 11(c), the unsteady solution at 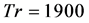 oscillates in the asymmetric six-vortex solutions. Then, we investigated time-dependent solution of
oscillates in the asymmetric six-vortex solutions. Then, we investigated time-dependent solution of  for
for 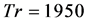 at Dn = 2000 as shown in Figure 12(a). It is found that the flow
at Dn = 2000 as shown in Figure 12(a). It is found that the flow
oscillates periodically, which is well justified by the power spectrum of the time evolution of 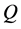 as shown in Figure 12(b), where only the line spectrum of the fundamental frequency and its harmonics are seen, which suggests that the flow is purely periodic at
as shown in Figure 12(b), where only the line spectrum of the fundamental frequency and its harmonics are seen, which suggests that the flow is purely periodic at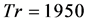 .
.
Secondary flow patterns and axial flow distribution for 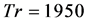 are then shown in Figure 12(c), where it is seen that the flow at
are then shown in Figure 12(c), where it is seen that the flow at 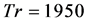 oscillates in the asymmetric six-vortex solutions. Figure 13(a) shows time evolution of
oscillates in the asymmetric six-vortex solutions. Figure 13(a) shows time evolution of 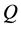 for
for 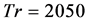 at Dn = 2000. It is found that the flow does not oscillate but goes steady-state, so that the unsteady solution at
at Dn = 2000. It is found that the flow does not oscillate but goes steady-state, so that the unsteady solution at 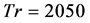 is a steady-state solution. Typical contours of secondary flow patterns and axial flow distribution for
is a steady-state solution. Typical contours of secondary flow patterns and axial flow distribution for 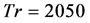 are also shown in Figure 13(b), where it is seen that the unsteady flow at
are also shown in Figure 13(b), where it is seen that the unsteady flow at 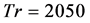 is an asymmetric six-vortex solution. It is noticed that axial flow is shifted near the outer wall of the duct as the rotational speed increases.
is an asymmetric six-vortex solution. It is noticed that axial flow is shifted near the outer wall of the duct as the rotational speed increases.
6. Conclusions
A numerical study on the fully developed two-dimensional flow of viscous incompressible fluid through a rotating curved rectangular duct of aspect ratio 1.5 and curvature 0.1 has been performed by using the spectral method, and covering a wide range of the Taylor number 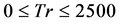 for the Dean number Dn = 2000. We investigated flow characteristics for positive rotation of the duct, and obtained secondary flow patterns and axial flow distribution for several values of
for the Dean number Dn = 2000. We investigated flow characteristics for positive rotation of the duct, and obtained secondary flow patterns and axial flow distribution for several values of  .
.
We obtained four branches of symmetric and asymmetric steady solutions with twoand multi-vortex solutions on various branches. The first branch consists of symmetric two-, fourand multi-vortex solutions. The second branch is composed of asymmetric two-, threeand four-vortex solutions; the third steady solution branch is composed of asymmetric two-, threeand four-vortex solutions, while the forth steady solution branch symmetric six-, eightand ten-vortex solutions. Then, In order to study the non-linear behavior of the unsteady solutions, time-evolution calculations as well as power spectrum of the unsteady solutions are performed, and it is found that the chaotic flow turns into steady-state flow through periodic flow in the scenario “chaotic ® multi-periodic ® periodic ® steady-state”, if Tr is increased from zero. It is found that at no ration, the flow is chaotic but as the rotational speed increases, the chaotic flow turns into steady-state flow through multi-periodic and periodic oscillations. The reason is that combined effect of centrifugal and Coriolis force counteract each other in a nonlinear manner which results in chaotic flow to turn into steady-state flow. Performing the power spectrum of the solutions was found to be fruitful for the investigation of unsteady flow behavior more accurately. Maximum axial flow was found to be shifted near the outer wall of the duct as the rotational speed increases.
Acknowledgements
Shinichiro Yanase, one of the authors, expresses his cordial thanks to the Japan Ministry of Education, CultureSports, Science and Technology for the financial support through the Grant-in-Aid for Scientific Research, No. 24560196.
References
- Ishigaki, H. (1993) Fundamental Characteristics of Laminar Flows in a Rotating Curved Pipe. Transactions of JSME, 59, 1494-1501.
- Ishigaki, H. (1996) Laminar Flow in Rotating Curved Pipes. Journal of Fluid Mechanics, 329, 373-388. http://dx.doi.org/10.1017/S0022112096008956
- Berger, S.A., Talbot, L. and Yao, L.S. (1983) Flow in Curved Pipes. Annual Review of Fluid Mechanics, 35, 461-512. http://dx.doi.org/10.1146/annurev.fl.15.010183.002333
- Nandakumar, K. and Masliyah, J.H. (1986) Swirling Flow and Heat Transfer in Coiled and Twisted Pipes. Advanced Transport Processes, 4, 49-112.
- Winters, K.H. (1987) A Bifurcation Study of Laminar Flow in a Curved Tube of Rectangular Cross-Section. Journal of Fluid Mechanics, 180, 343-369. http://dx.doi.org/10.1017/S0022112087001848
- Mondal, R.N., Kaga, Y., Hyakutake, T. and Yanase, S. (2007) Bifurcation Diagram for Two-Dimensional Steady Flow and Unsteady Solutions in a Curved Square Duct. Fluid Dynamics Research, 39, 413-446. http://dx.doi.org/10.1016/j.fluiddyn.2006.10.001
- Selmi, M., Namdakumar, K. and Finlay, W.H. (1994) A Bifurcation Study of Viscous Flow through a Rotating Curved Duct. Journal of Fluid Mechanics, 262, 353-375. http://dx.doi.org/10.1017/S0022112094000534
- Selmi, M. and Namdakumar, K. (1999) Bifurcation Study of the Flow through Rotating Curved Ducts. Physics of Fluids, 11, 2030-2043. http://dx.doi.org/10.1063/1.870066
- Yamamoto, K., Yanase, S. and Alam, M.M. (1999) Flow through a Rotating Curved Duct with Square Cross-Section. Journal of the Physical Society of Japan, 68, 1173-1184. http://dx.doi.org/10.1143/JPSJ.68.1173
- Mondal, R.N., Islam, M.R., Uddin, M.S. and Datta, A.K. (2010) Flow through a Rotating Curved Square Duct: The Case of Positive Rotation. Journal of Physical Science, 14, 145-163.
- Wang, L.Q. and Cheng, K.C. (1996) Flow Transitions and Combined Free and Forced Convective Heat Transfer in Rotating Curved Channels: The Case of Positive Rotation. Physics of Fluids, 8, 1553-1573. http://dx.doi.org/10.1063/1.868930
- Zhang, J.S., Zhang, B.Z. and Jü, J. (2001) Fluid Flow in a Rotating Curved Rectangular Duct. International Journal of Heat and Fluid Flow, 22, 583-592. http://dx.doi.org/10.1016/S0142-727X(01)00126-6
- Mondal, R.N., Alam, M.M. and Yanase, S. (2007) Numerical Prediction of Non-Isothermal Flows through a Rotating Curved Duct with Square Cross Section. Thammasat International Journal of Science and Technology, 12, 24-43.
- Mondal, R.N., Datta, A.K. and Mondal, B. (2011) Bifurcation Study of Thermal Flows through a Rotating Curved Square Duct. Bangladesh Journal of Scientific and Industrial Research, 48, 59-70.
- Yamamoto, K., Wu, X., Nozaki, K. and Hayamizu, Y. (2006) Visualization of Taylor-Dean Flow in a Curved Duct of Square Cross-Section. Fluid Dynamics Research, 38, 1-18. http://dx.doi.org/10.1016/j.fluiddyn.2005.09.002
- Nobari, M.R.H., Nousha, A. and Damangir, E. (2009) A Numerical Investigation of Flow and Heat Transfer in Rotating U-Shaped Square Ducts. International Journal of Thermal Sciences, 48, 590-601. http://dx.doi.org/10.1016/j.ijthermalsci.2008.04.001
- Yanase, S. and Nishiyama, K. (1988) On the Bifurcation of Laminar Flows through a Curved Rectangular Tube. Journal of the Physical Society of Japan, 57, 3790-3795. http://dx.doi.org/10.1143/JPSJ.57.3790
- Yanase, S., Kaga, Y. and Daikai, R. (2002) Laminar Flow through a Curved Rectangular Duct over a Wide Range of the Aspect Ratio. Fluid Dynamics Research, 31, 151-183. http://dx.doi.org/10.1016/S0169-5983(02)00103-X
- Yang, T. and Wang, L. (2003) Bifurcation and Stability of Forced Convection in Rotating Curved Ducts of Square Cross Section. International Journal of Heat and Mass Transfer, 46, 613-629. http://dx.doi.org/10.1016/S0017-9310(02)00329-0
- Wang, L.Q. and Yang, T.L. (2004) Multiplicity and Stability of Convection in Curved Ducts: Review and Progress. Advances in Heat Transfer, 38, 203-256. http://dx.doi.org/10.1016/S0065-2717(04)38004-4
- Yanase, S., Mondal, R.N. and Kaga, Y. (2005) Numerical Study of Non-Isothermal Flow with Convective Heat Transfer in a Curved Rectangular Duct. International Journal of Thermal Sciences, 44, 1047-1060. http://dx.doi.org/10.1016/j.ijthermalsci.2005.03.013
- Mondal, R.N., Kaga, Y., Hyakutake, T. and Yanase, S. (2006) Effects of Curvature and Convective Heat Transfer in Curved Square Duct Flows. Journal of Fluids Engineering, ASME Journals, 128, 1013-1023. http://dx.doi.org/10.1115/1.2236131
- Gottlieb, D. and Orazag, S.A. (1977) Numerical Analysis of Spectral Methods. Society for Industrial and Applied Mathematics, Philadelphia. http://dx.doi.org/10.1137/1.9781611970425
- Keller, H.B. (1987) Lectures on Numerical Methods in Bifurcation Problems. Springer, Berlin.
- Mondal, R.N. (2006) Isothermal and Non-Isothermal Flows through Curved Duct with Square and Rectangular CrossSection. Ph.D. Thesis, Okayama University, Okayama.


 (a)
(a)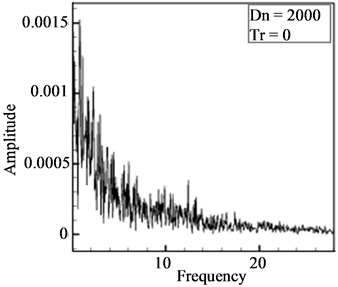 (b)
(b) (c)
(c)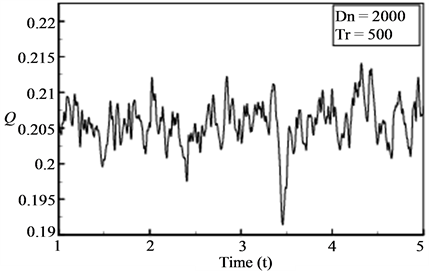 (a)
(a) (b)
(b)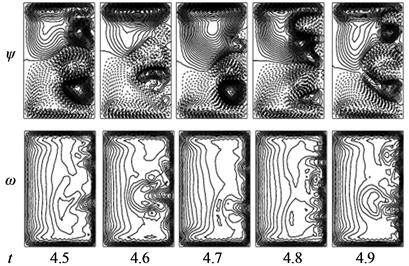 (c)
(c)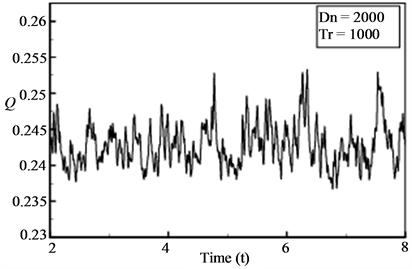 (a)
(a)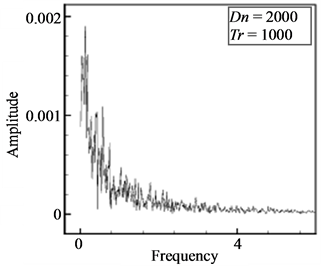 (b)
(b)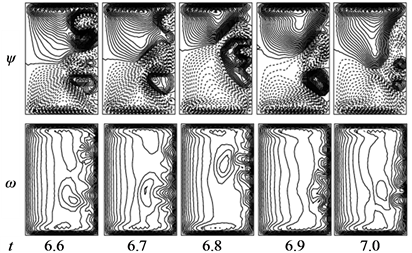 (c)
(c)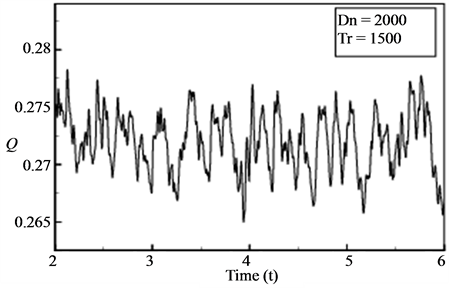 (a)
(a)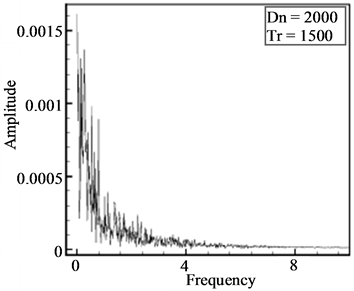 (b)
(b)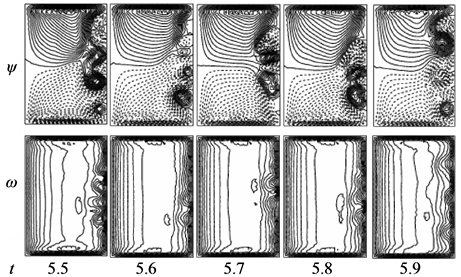 (c)
(c)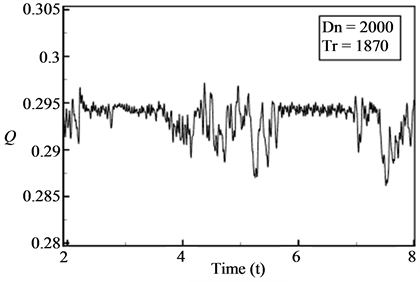 (a)
(a)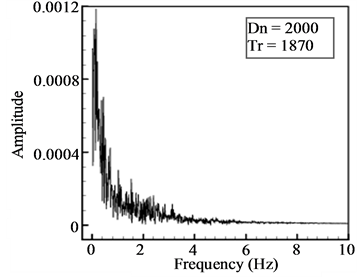 (b)
(b) (c)
(c)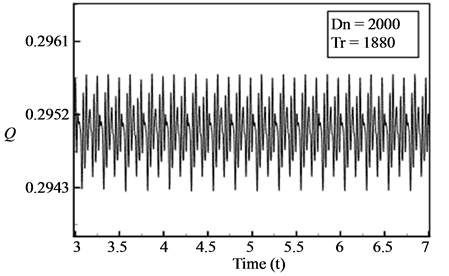 (a)
(a)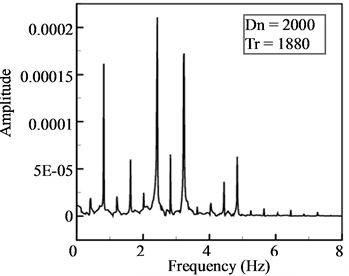 (b)
(b)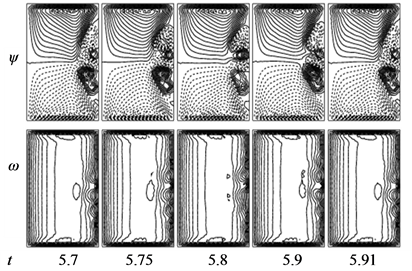 (c)
(c) (a)
(a)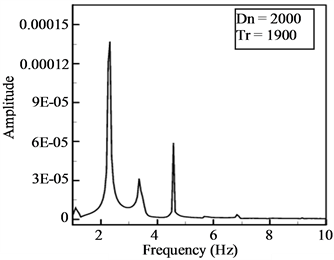 (b)
(b) (c)
(c)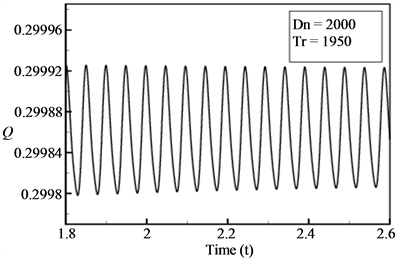 (a)
(a)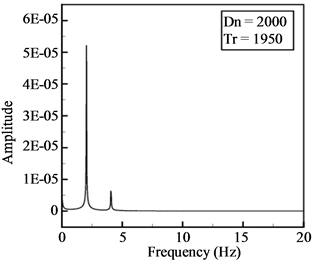 (b)
(b)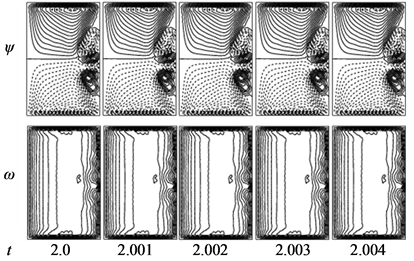 (c)
(c) (a)
(a) (b)
(b)