Open Journal of Fluid Dynamics
Vol.2 No.4(2012), Article ID:25400,4 pages DOI:10.4236/ojfd.2012.24011
Heat Transfer with Viscous Dissipation in Couette-Poiseuille Flow under Asymmetric Wall Heat Fluxes
1Faculty of Engineering, Multimedia University, Cyberjaya, Malaysia
2School of Mechanical & Aerospace Engineering, Nanyang Technological University, Singapore City, Singapore
3Faculty of Engineering & Technology, Multimedia University, Jalan Ayer Keroh Lama, Melaka, Malaysia
Email: franciscasheela@hotmail.com
Received June 29, 2012; revised August 5, 2012; accepted August 13, 2012
Keywords: Viscous Dissipation; Couette-Poiseuille Flow; Newtonian Fluid; Nusselt Number; Brinkman Number; Constant Heat-Flux
ABSTRACT
Analytical solutions of temperature distributions and the Nusselt numbers in forced convection are reported for flow through infinitely long parallel plates, where the upper plate moves in the flow direction with constant velocity and the lower plate is kept stationary. The flow is assumed to be laminar, both hydro-dynamically and thermally fully developed, taking into account the effect of viscous dissipation of the flowing fluid. Both the plates being kept at specified and at different constant heat fluxes are considered as thermal boundary conditions. The solutions obtained from energy equation are in terms of Brinkman number, dimensionless velocity and heat flux ratio. These parameters greatly influence and give complete understanding on heat transfer rates that has potentials for designing and analyzing energy equipment and processes.
1. Introduction
Flow of Newtonian fluids through various channels is of practical importance and heat transfer is dependent on flow conditions such as flow geometry and physical properties. Investigations in heat transfer behavior through various channels showed that the effect of viscous dissipation cannot be neglected for some applications, such as flow through micro-channels, small conduits and extrusion at high speeds. The thermal development of forced convection through infinitely long fixed parallel plates, both plates having specified constant heat flux had been investigated [1-5]. For the same but filled by a saturated porous medium, heat transfer analysis was done where the walls were kept at uniform wall temperature with the effect of viscous dissipation and axial conduction taken into account [6]. In [7], it was concluded that in a porous medium, the absence of viscous dissipation effect can have great impact. For the horizontal double passage channel, uniform wall temperature with asymmetric and symmetric heating and the effect of viscous dissipation had been investigated [8].
For the pipe flow, where the walls are kept either at constant heat flux or constant wall temperature, analytical solution is obtained for both hydro-dynamically and thermally fully developed and thermally developing Newtonian fluid flow, considering the effect of viscous dissipation [9,10].
Analytical solution with the effect of viscous dissipation was derived for Couette-Poiseuille flow of nonlinear visco-elastic fluids and with the simplified Phan-ThienTanner fluid between parallel plates, with stationary plate subjected to constant heat flux and the other plate moving with constant velocity but insulated [11-13]. Numerical solution of fully developed laminar heat transfer of power-law non-Newtonian fluids in plane Couette flow, with constant heat flux at one wall with other wall insulated had been investigated [14] and analytical solution was derived for Newtonian fluid [15].
A numerical investigation had been done to find the heat transfer for the simultaneously developing steady laminar flow, where the fluid was considered to be viscous non-Newtonian described by a power-law model flowing between two parallel plates with several different thermal boundary conditions [16]. When a thin slab was symmetrically heated on both sides, the hyperbolic heat conduction equation was solved analytically [17]. Considering the effect of viscous dissipation and pressure stress work of the fluid, the steady laminar boundary layer flow along a vertical stationary isothermal plate was studied. The variation of wall heat transfer and wall shear stress along the plate was discussed [18].
The Bingham fluid was assumed to be flowing in between two porous parallel plates. With the slip effect at the porous walls, the analytical solutions were obtained for the Couette-Poiseuille flow [19]. Numerical evaluation for developing temperature profiles by a finite-difference method were carried out for non-Newtonian fluid through parallel plates and circular ducts. The effects of viscous dissipation and axial heat conduction were taken into account. Graphical representation of Nusselt numbers were noted for various parameters [20]. The thermal entrance region of a horizontal parallel plate channel, where the lower plate was heated isothermally and the upper plate was cooled isothermally was considered. Numerical results were found on the onset of instability for longitudinal vortices, with effect of viscous dissipation [21]. A numerical analysis was carried out, taking viscous dissipation into account for pseudo-plastic nonNewtonian fluids aligned with a semi-infinite plate [22].
From the literature survey, it is observed that heat transfer analysis with effect of viscous dissipation is not found for the Couette-Poiseuille flow with both the plates being kept at specified but different constant heat fluxes. The heat transfer analysis with one plate moving is a different fundamental problem worth pursuing. This study is necessary specifically in the design of special heat exchangers and other devices where the dimensions have to be kept very small. Hence, the case of lower plate being fixed and the upper plate moving with constant velocity, both being imposed to different but constant heat fluxes is considered. The energy equation is solved leading to expressions in temperature profiles and Nusselt number, that could be useful to industrial applications.
2. Statement of Problem and Mathematical Formulation
Consider two flat infinitely long parallel plates distanced W or 2 apart, where the upper plate is moving with constant velocity U and the lower plate is fixed. The coordinate system chosen is shown in Figure 1. The flow through the plates is considered at a sufficient distance from the entrance such that it is both hydro-dynamically and thermally fully developed. The axial heat conduction in the fluid and through the wall is assumed to be negligible. The fluid is assumed to be Newtonian and with constant properties. The thermal boundary conditions are the upper plate is kept at constant heat flux while the lower plate at different constant heat flux.
The momentum equation in the x-direction is described as
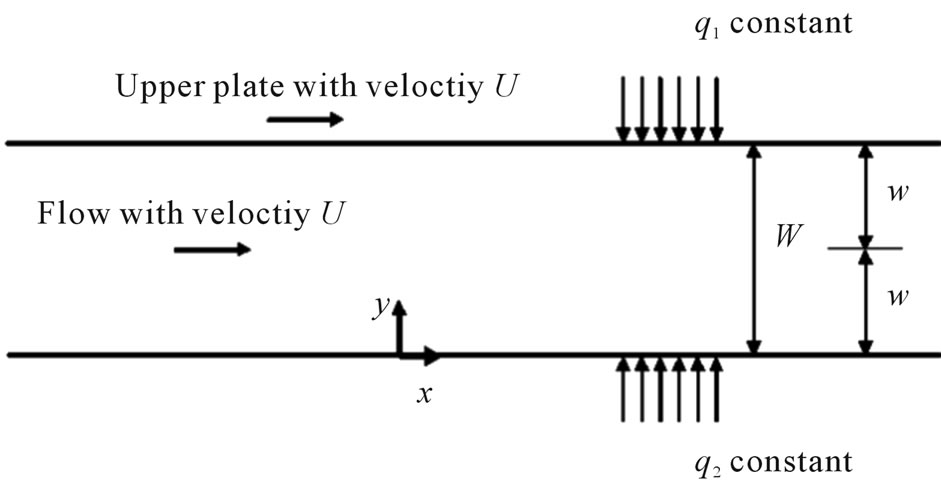
Figure 1. Notation to the problem.
 (1)
(1)
where u is the velocity of the fluid, 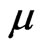 is the dynamic viscosity, P is the pressure.
is the dynamic viscosity, P is the pressure.
The velocity boundary conditions are u = 0 when y = 0 and u = U when y = W.
Using the following dimensionless parameters:
 (2)
(2)
the well-known velocity-distribution is [15],
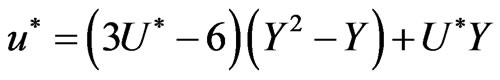 , (3)
, (3)
where the mean velocity (um) is given by
 (4)
(4)
For the above equation, expression for u is obtained by solving the momentum Equation (1).
The energy equation, including the effect of viscous dissipation, is given by
 , (5)
, (5)
where the second term on the right-hand side is the viscous-dissipative term. In accordance to the assumption of a thermally fully developed flow with uniformly heated boundary walls, the longitudinal conduction term is neglected in the energy equation [23]. Following this, the temperature gradient along the axial direction is independent of the transverse direction and given as
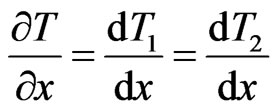 , (6)
, (6)
where  and
and 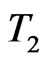 are the upper and lower wall temperatures, respectively.
are the upper and lower wall temperatures, respectively.
By taking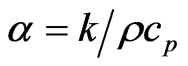 , introducing the non-dimensional quantity
, introducing the non-dimensional quantity
 , (7)
, (7)
and defining a dimensionless constant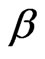 ,
,
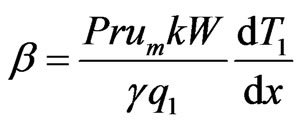 , (8)
, (8)
and modified Brinkman number 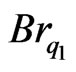 as
as
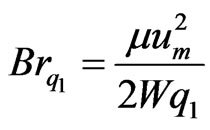 , (9)
, (9)
Equation (5) can be written as
 (10)
(10)
The thermal boundary conditions are
 (11)
(11)
The solution of Equation (10) under the above thermal boundary conditions can be obtained as
 (12)
(12)
To evaluate 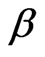 in the above equation, a third boundary condition is required:
in the above equation, a third boundary condition is required:
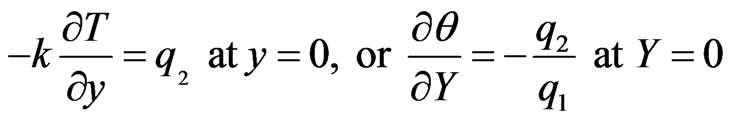 . (13)
. (13)
By substituting Equation (13) into Equation (12), 
can be expressed as
 (14)
(14)
Therefore, the solution of Equation (10) under the above thermal boundary conditions can be written in a simplified form as
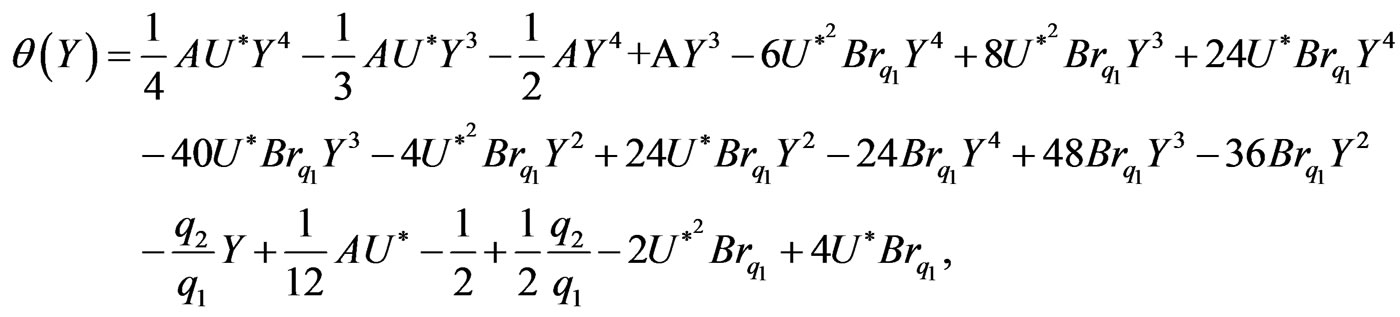 (15)
(15)
where
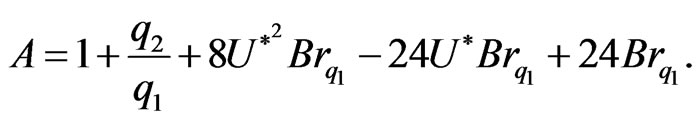 (16)
(16)
In fully developed flow, it is usual to utilize the mean fluid-temperature, 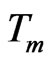 , rather than the centerline temperature, when defining the Nusselt number. Thus mean or bulk temperature is given by
, rather than the centerline temperature, when defining the Nusselt number. Thus mean or bulk temperature is given by
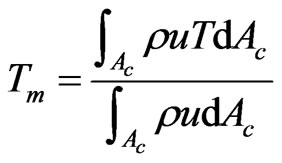 , (17)
, (17)
with 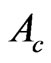 the cross-sectional area of the channel and the denominator on the right-hand side of Equation (17) can be written as
the cross-sectional area of the channel and the denominator on the right-hand side of Equation (17) can be written as
 . (18)
. (18)
Using Equations (3) and (15), the numerator of Equation (17) can be found. Therefore the dimensionless mean temperature is given by
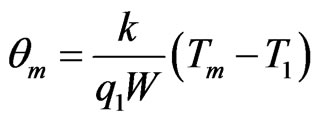 . (19)
. (19)
At this point, the convective heat transfer coefficient can be evaluated by the equation
 . (20)
. (20)
Defining Nusselt number to be
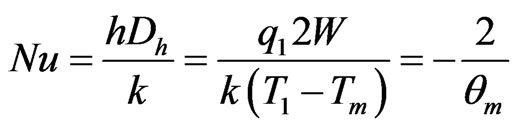 , (21)
, (21)
where Dh is the hydraulic diameter defined by Dh = 2W, the expression for Nusselt number can be shown to be
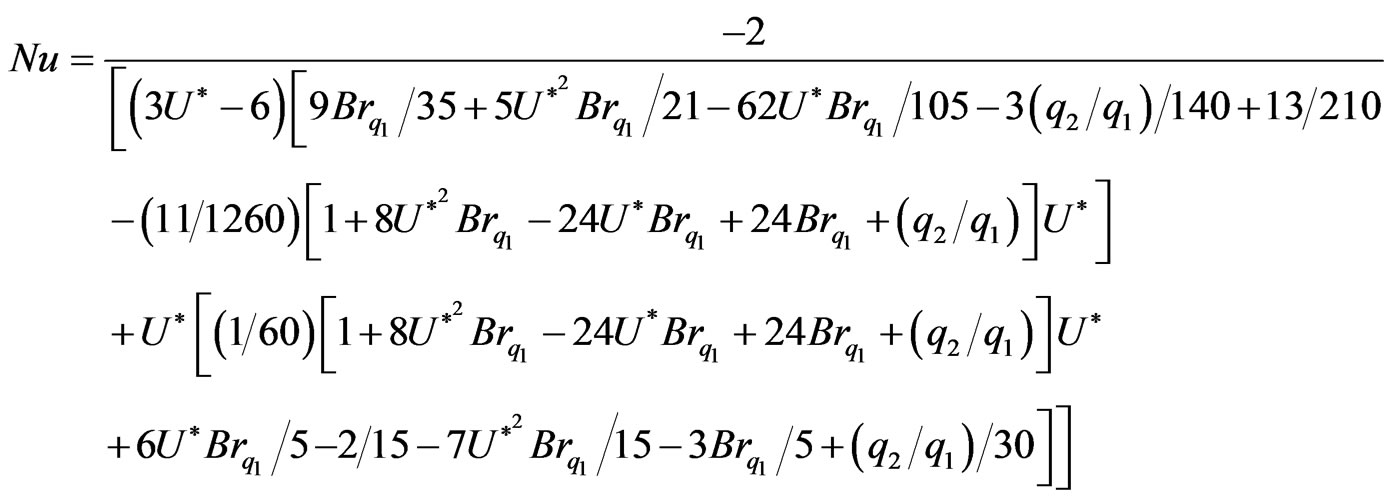 (22)
(22)
When q2 = 0,
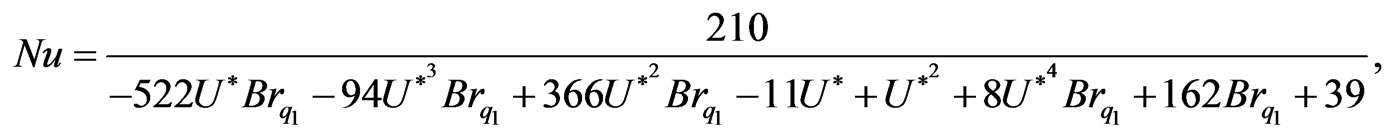 (23)
(23)
agreeing with reference [15].
Explicit expressions for Nusselt number for various values of U*,  and
and  are given in the following discussions.
are given in the following discussions.
3. Graphical Results and Discussions
For the purpose of discussion on the behavior of the Couette-Poiseuille flow, two types of graphs based on the analytical solutions are made. The temperature profile in the channel is plotted with variations of various parameters to indicate the heated region, and the Nusselt number is plotted to reveal the heat transfer characteristics of the flow.
3.1. Temperature Profiles against the Channel Width for Various Parameters
3.1.1. Temperature Profiles for the Case of Insulated Lower Plate
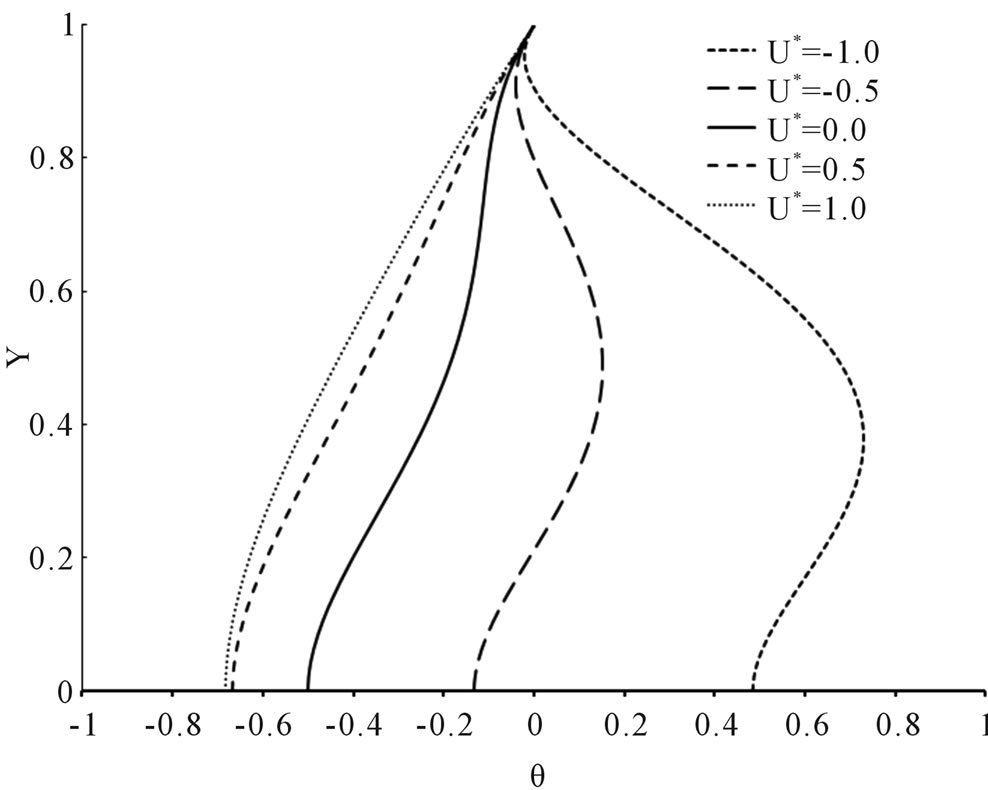
Figure 2 shows the dimensionless temperature profiles of  versus Y, where the lower plate is insulated at five dimensionless velocities U* = −1.0, −0.5, 0.0, 0.5 and 1.0, and at six selected
versus Y, where the lower plate is insulated at five dimensionless velocities U* = −1.0, −0.5, 0.0, 0.5 and 1.0, and at six selected 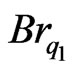 values from −0.01 to 0.5, as shown in (a) to (f). The temperature distributions have similar pattern but different shapes, and all the curves converge at Y = 1, θ equal to 0, by definition. At Y = 0, the curves are vertical to satisfy the insulated condition. As expected, generally the motion of the upper plate tends to impart more heat into the fluid layers that are dragged along, unless off-set by the viscous dissipation effects. It is observed that when
values from −0.01 to 0.5, as shown in (a) to (f). The temperature distributions have similar pattern but different shapes, and all the curves converge at Y = 1, θ equal to 0, by definition. At Y = 0, the curves are vertical to satisfy the insulated condition. As expected, generally the motion of the upper plate tends to impart more heat into the fluid layers that are dragged along, unless off-set by the viscous dissipation effects. It is observed that when 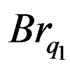 = −0.01, 0.0, 0.01 and 0.1, the temperature distribution is negative which implies there is decrease in heat transfer, whereas when
= −0.01, 0.0, 0.01 and 0.1, the temperature distribution is negative which implies there is decrease in heat transfer, whereas when 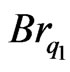 = −0.1 and 0.5, θ manifests in a different way such that θ takes both negative and positive values.
= −0.1 and 0.5, θ manifests in a different way such that θ takes both negative and positive values.
3.1.2. Temperature Profiles for a Fixed Brinkman Number for Various Heat Flux Ratios
The effect of viscous dissipation is seen in the value of modified Brinkman number. It is interesting to observe the behavior of the temperature profiles for various heat flux ratios for a fixed modified Brinkman number and hence to note the effect of viscous dissipation. In Figure 3, for a 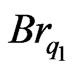 value of 0.01, the temperature distribution is investigated at U* = −1.0, −0.5, 0.0, 0.5 and 1.0 for various heat flux ratios. When
value of 0.01, the temperature distribution is investigated at U* = −1.0, −0.5, 0.0, 0.5 and 1.0 for various heat flux ratios. When , the values of theta are all negative. For the equal heat fluxes, for U* = −1.0, −0.5 and 0.0, theta takes only negative values, but for
, the values of theta are all negative. For the equal heat fluxes, for U* = −1.0, −0.5 and 0.0, theta takes only negative values, but for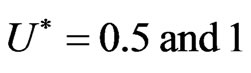 , theta takes both positive as well as negative values. When
, theta takes both positive as well as negative values. When  and 10.0, theta takes both positive as well as negative values. For
and 10.0, theta takes both positive as well as negative values. For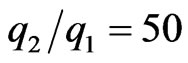 , when the upper plate moves in the negative direction with values U* = −1.0, −0.5, theta takes both positive as well as negative values and when the upper plate is fixed and moves in the positive direction with values U* = 0.5 and 1.0, theta takes positive values. As expected again, all the curves converge at Y = 1.
, when the upper plate moves in the negative direction with values U* = −1.0, −0.5, theta takes both positive as well as negative values and when the upper plate is fixed and moves in the positive direction with values U* = 0.5 and 1.0, theta takes positive values. As expected again, all the curves converge at Y = 1.
3.2. Nusselt Number Variations
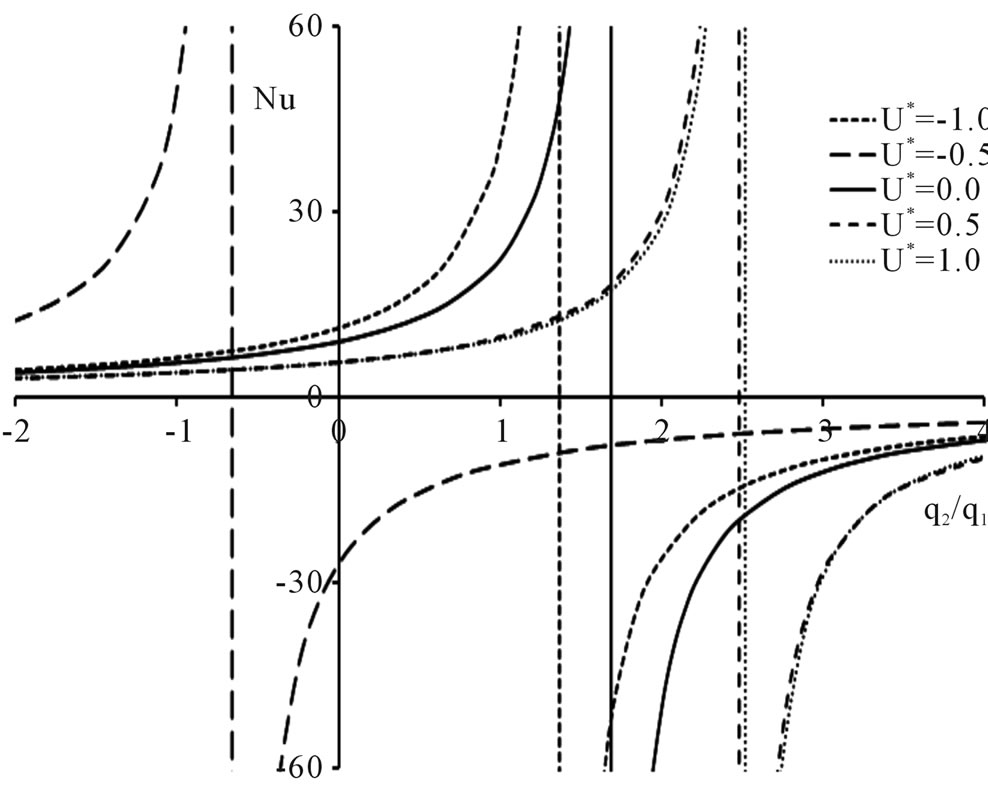
Figure 4 shows the plots of Nusselt number versus the heat flux ratio 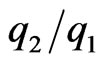 at U* = −1.0, −0.5, 0.0, 0.5 and 1.0 at various
at U* = −1.0, −0.5, 0.0, 0.5 and 1.0 at various  values. The hyperbolic curves have asymptotes occurring at different
values. The hyperbolic curves have asymptotes occurring at different 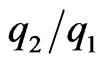 values. It is observed that, for the specified values of
values. It is observed that, for the specified values of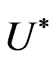 , when
, when 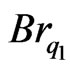 = −0.01, 0.0, 0.01 and 0.1, the asymptotes fall to the positive direction of
= −0.01, 0.0, 0.01 and 0.1, the asymptotes fall to the positive direction of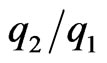 , whereas when
, whereas when 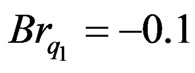 at
at , the asymptote falls at
, the asymptote falls at 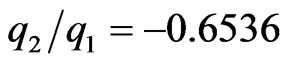 and when
and when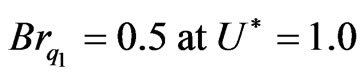 , the asymptote falls at
, the asymptote falls at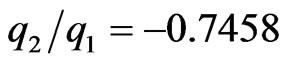 , as given in Table 1.
, as given in Table 1.
4. Conclusion
Heat transfer with the effect of viscous dissipation has been analysed. Analytical expressions for Nusselt number have been obtained for fully developed Newtonian fluid flow between infinitely long parallel plates, where the lower plate is fixed and the upper plate is moving with constant velocity. When both plates are kept at
 (a)
(a)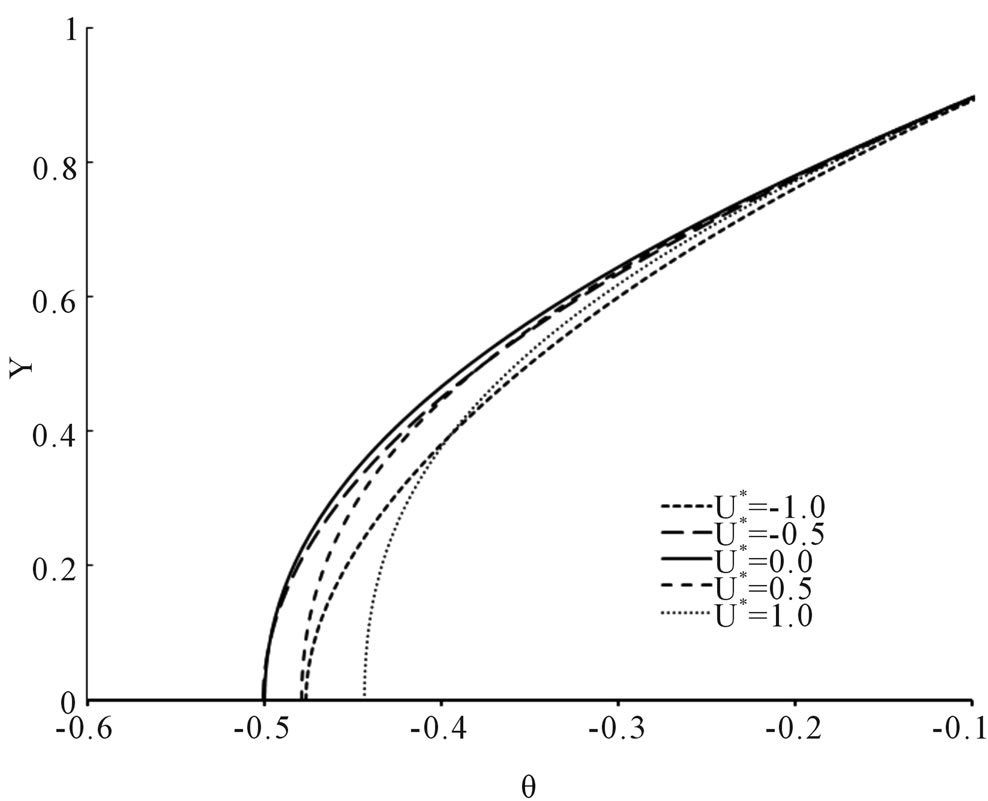 (b)
(b)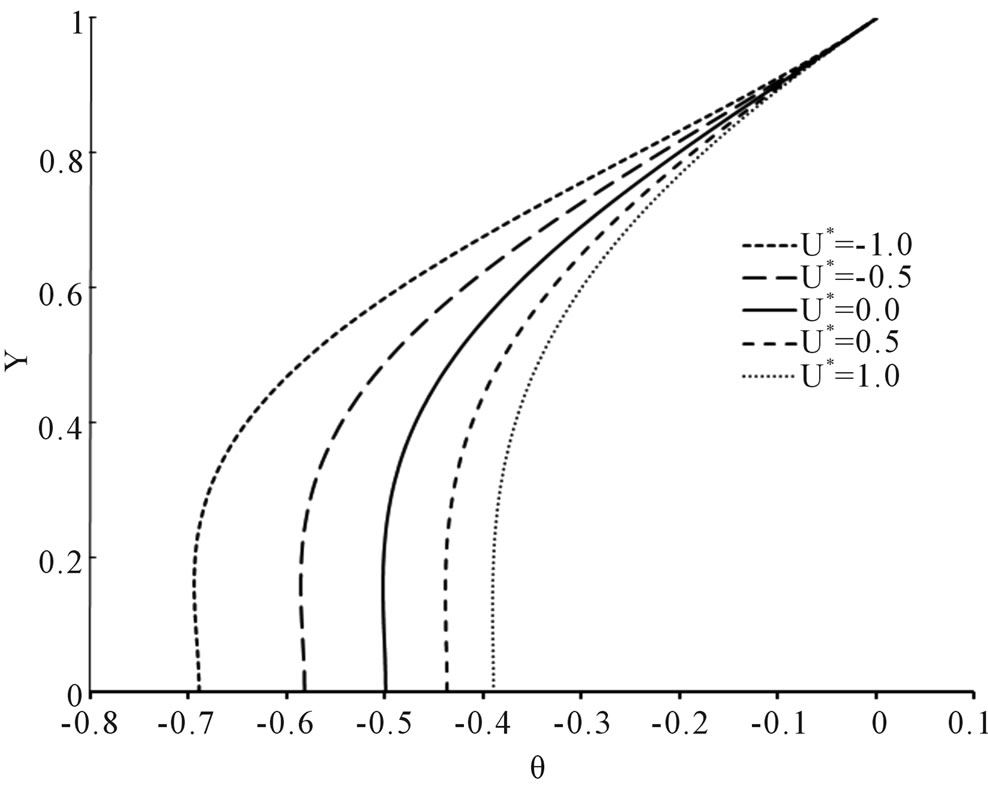 (c)
(c)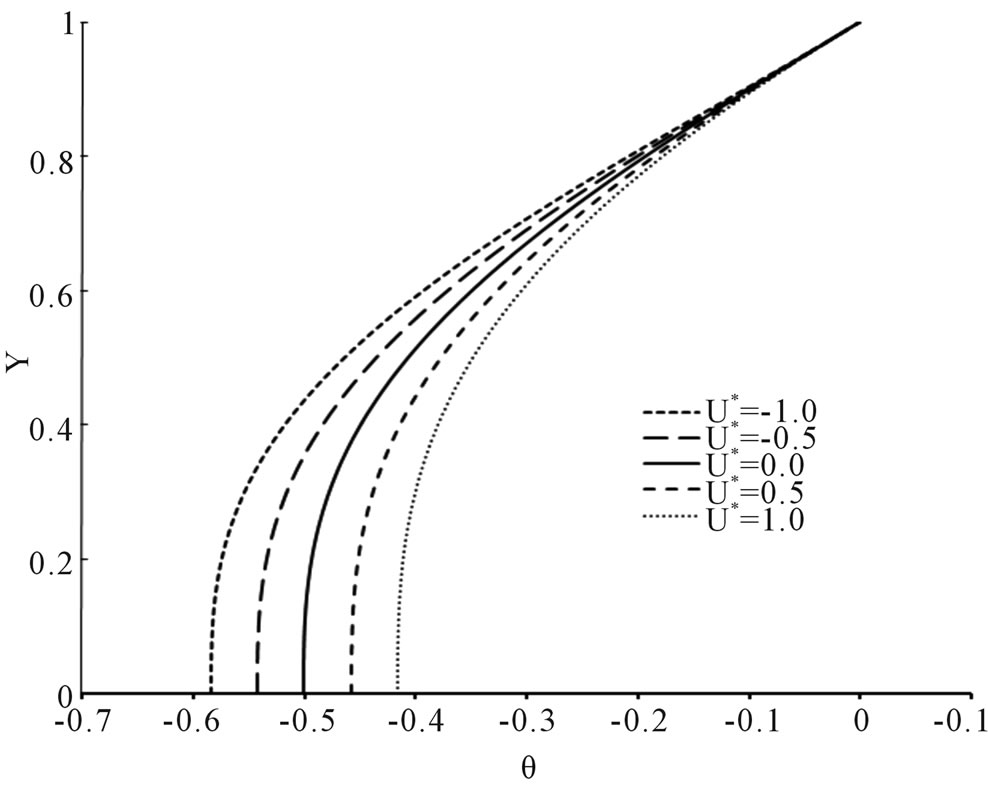 (d)
(d)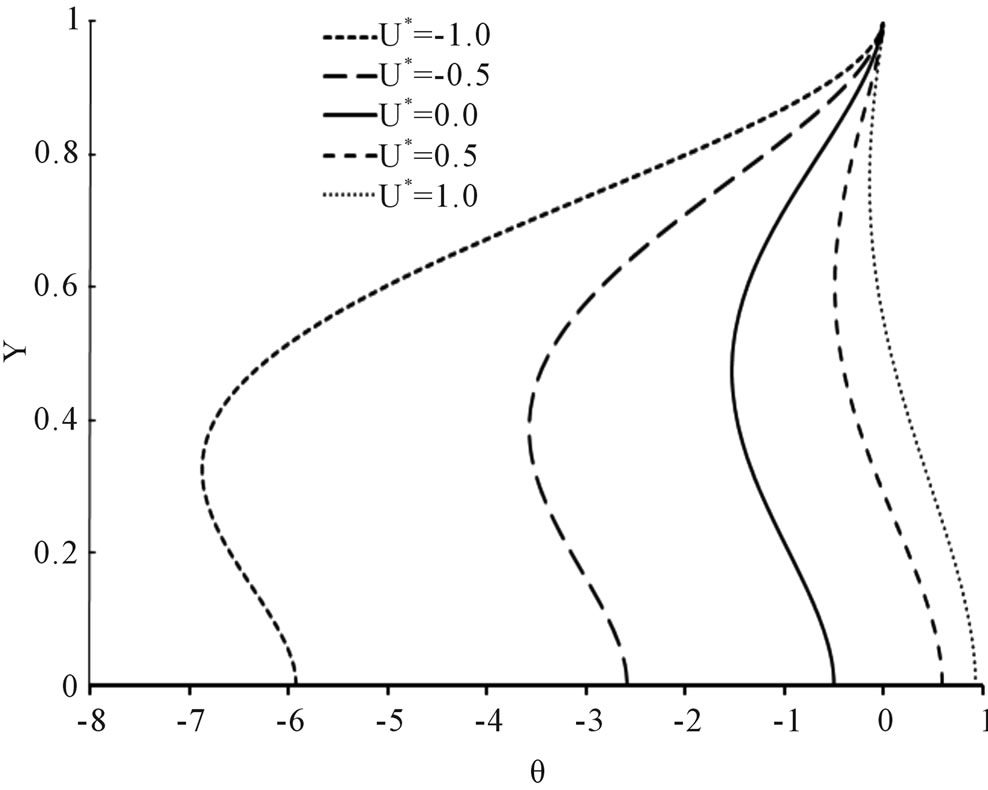 (e)
(e)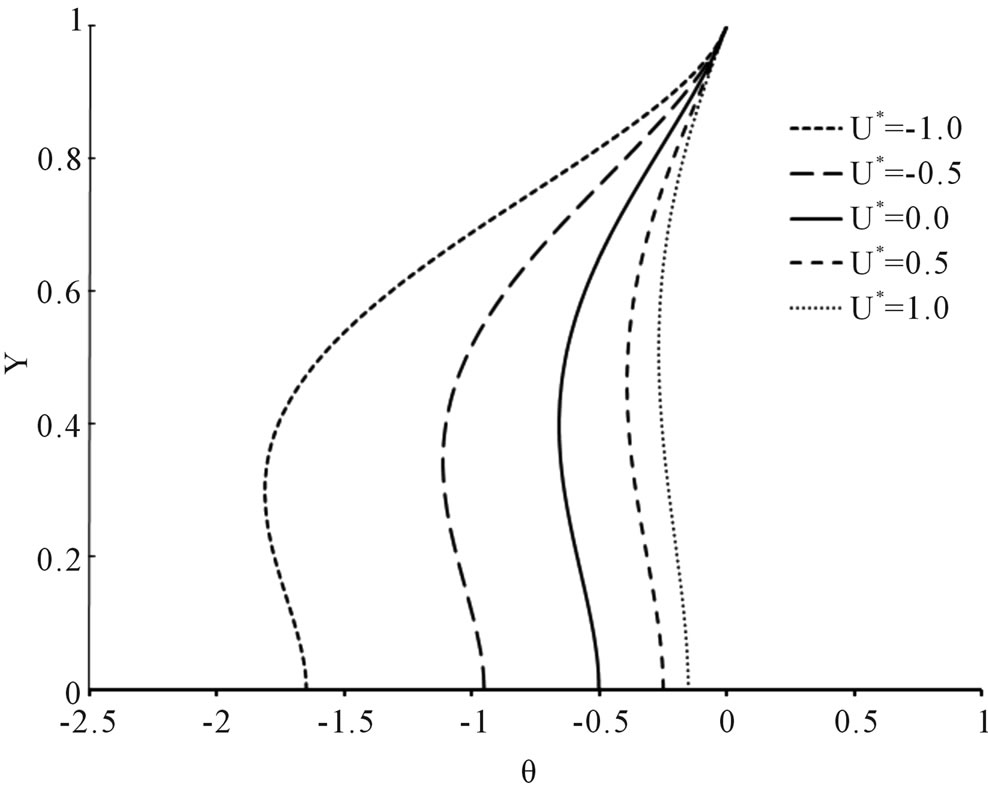 (f)
(f)
Figure 2. Temperature profiles at U* = −1.0, −0.5, 0.0, 0.5 and 1.0 at various for the case of q2/q1 = 0. (a) Brq1 = −0.01; (b) Brq1 = −0.10; (c) Brq1 = 0.00; (d) Brq1 = 0.01; (e) Brq1 = 0.10; (f) Brq1 = 0.50.
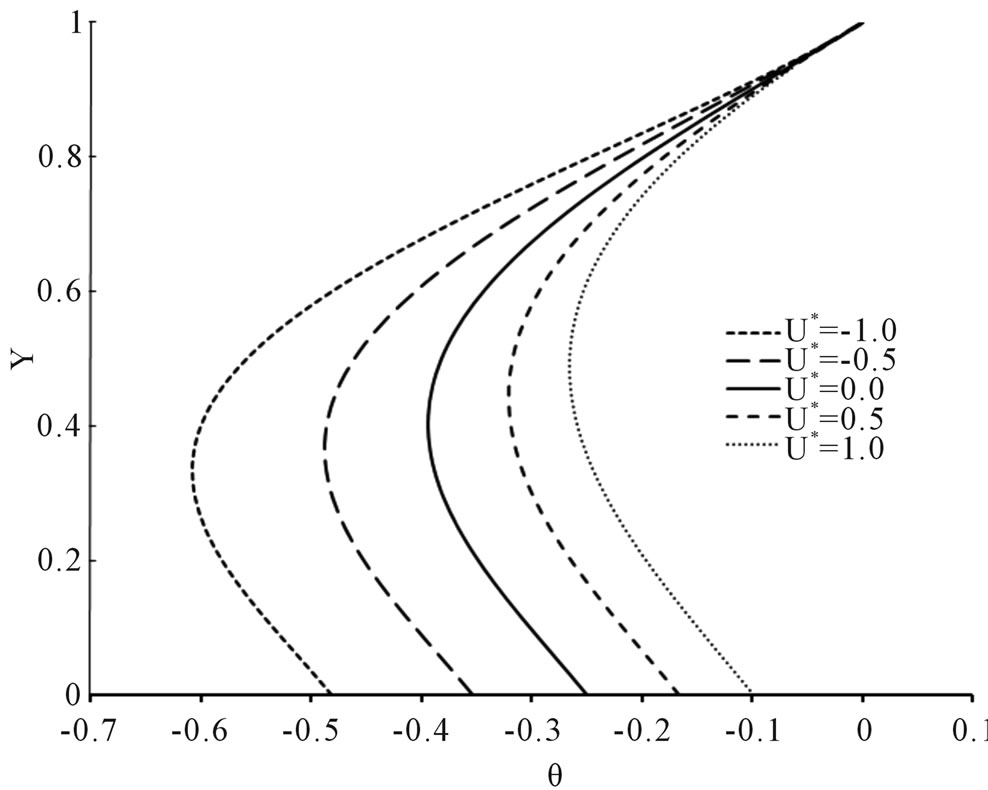 (a)
(a)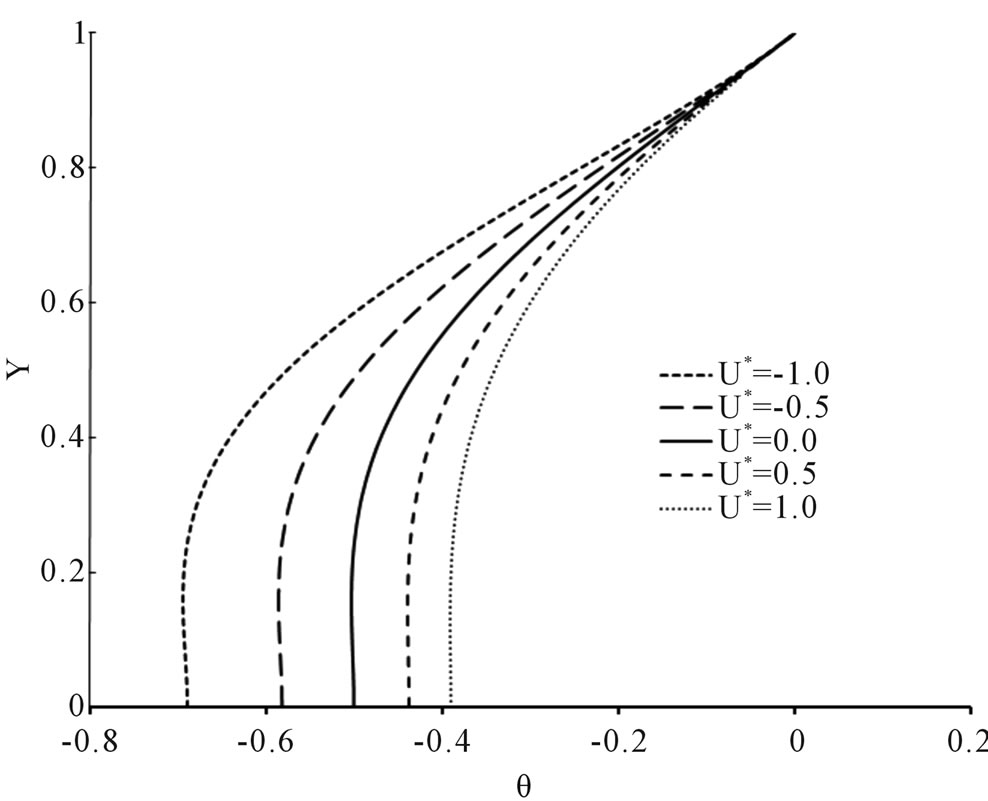 (b)
(b) (c)
(c) (d)
(d) (e)
(e)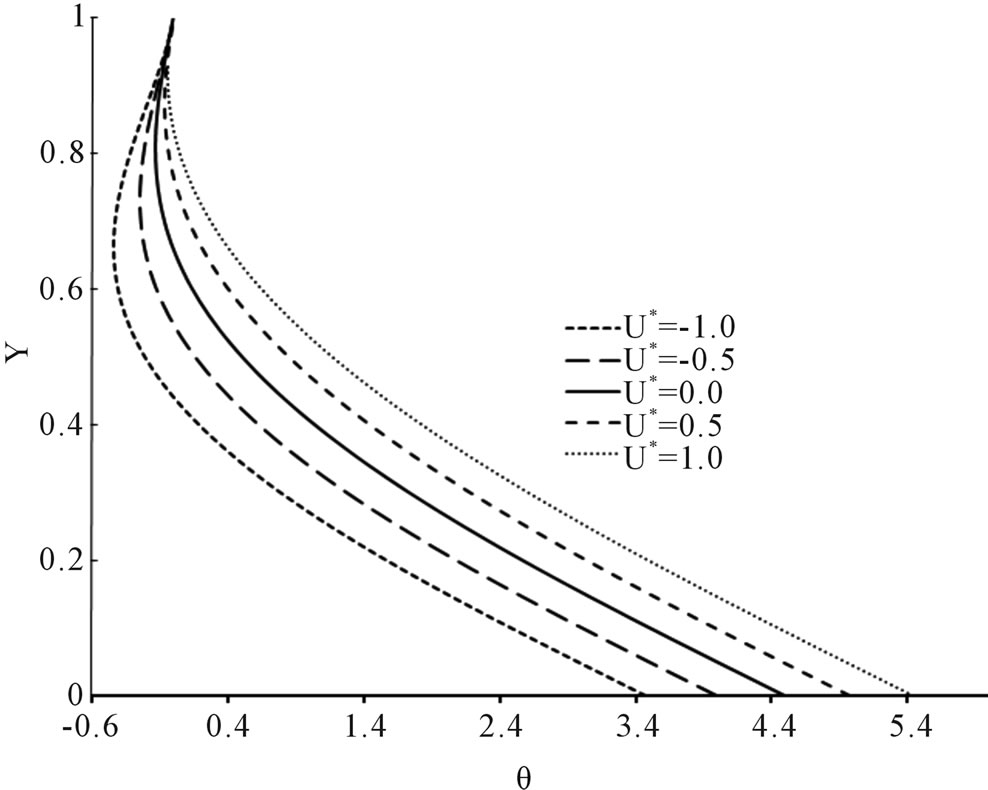 (f)
(f)
Figure 3. Temperature profiles at U* = −1.0, −0.5, 0.0, 0.5 and 1.0 at various q2/q1, for the case of Brq1 = 0.01. (a) q2/q1 = 0.0; (b) q2/q1 = 0.50; (c) q2/q1 = 1.0; (d) q2/q1 = 2.0; (e) q2/q1 = 10.0; (f) q2/q1 = 50.0.
 (a)
(a)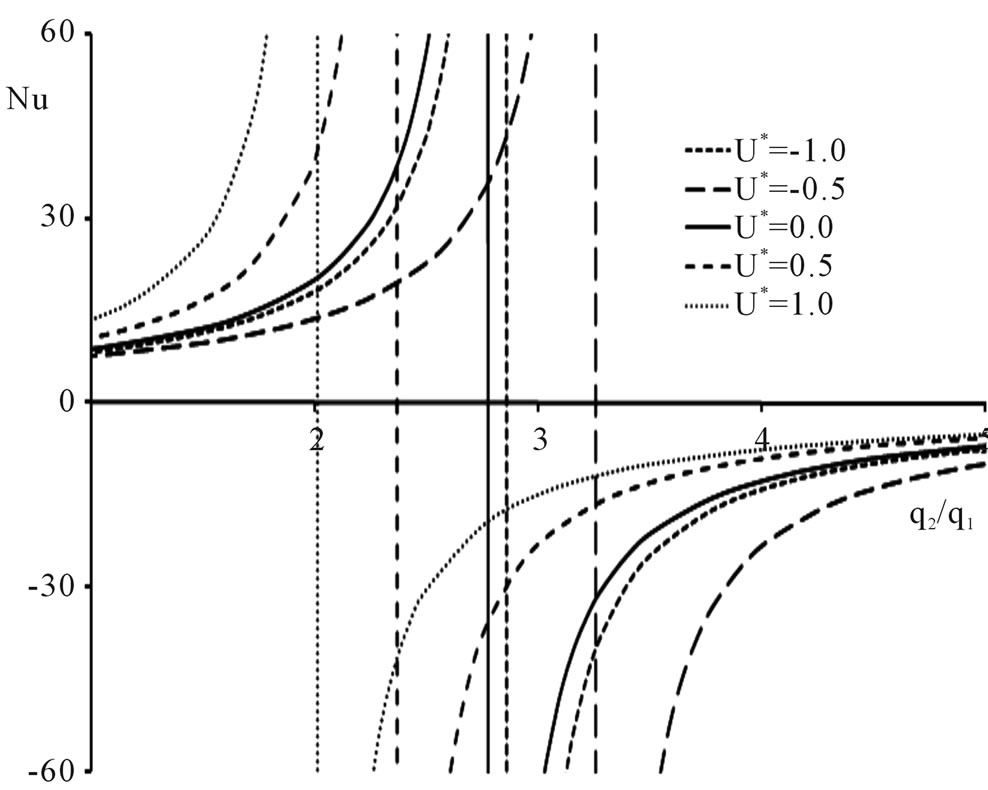 (b)
(b)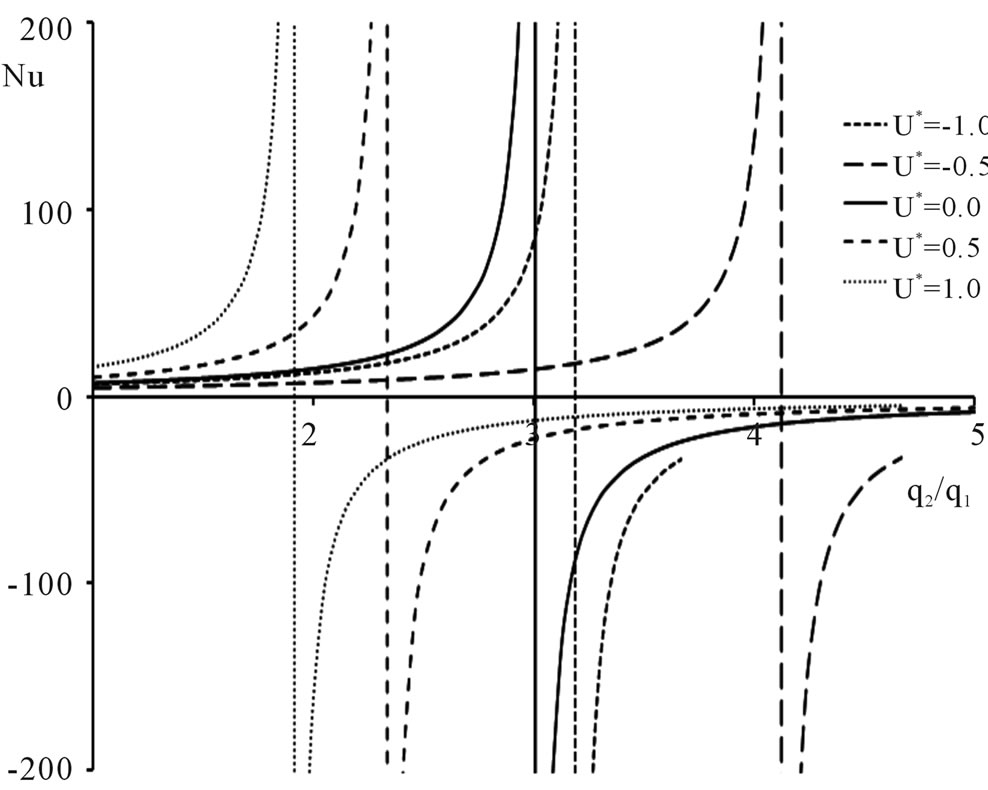 (c)
(c) (d)
(d)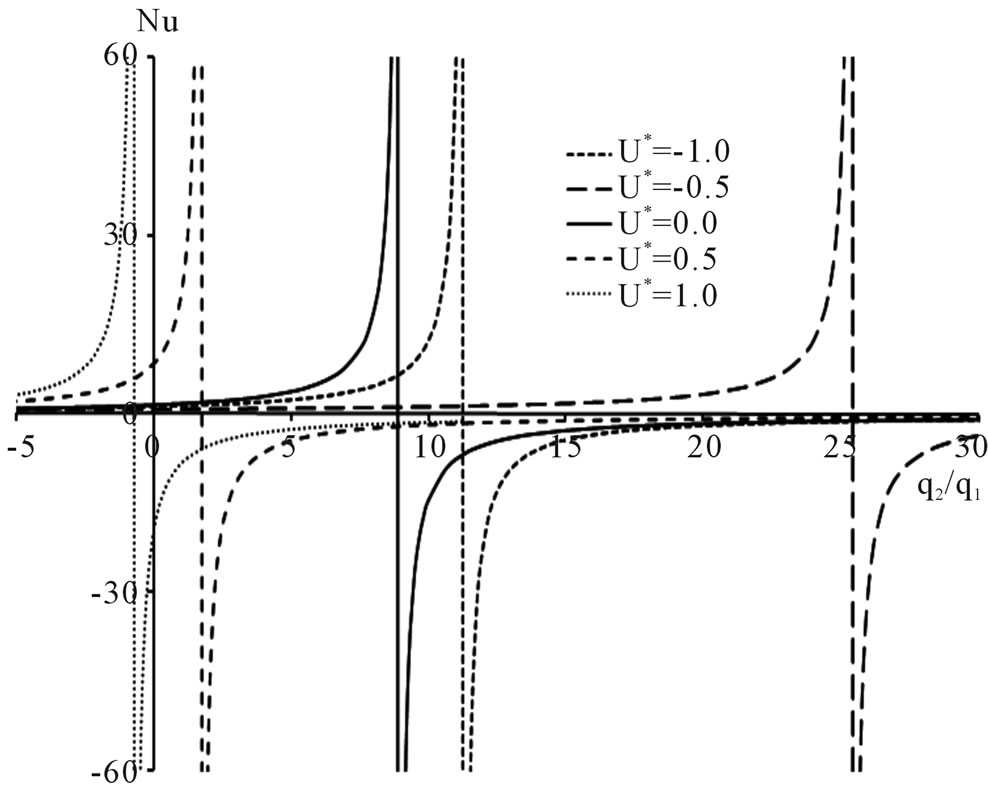 (e)
(e)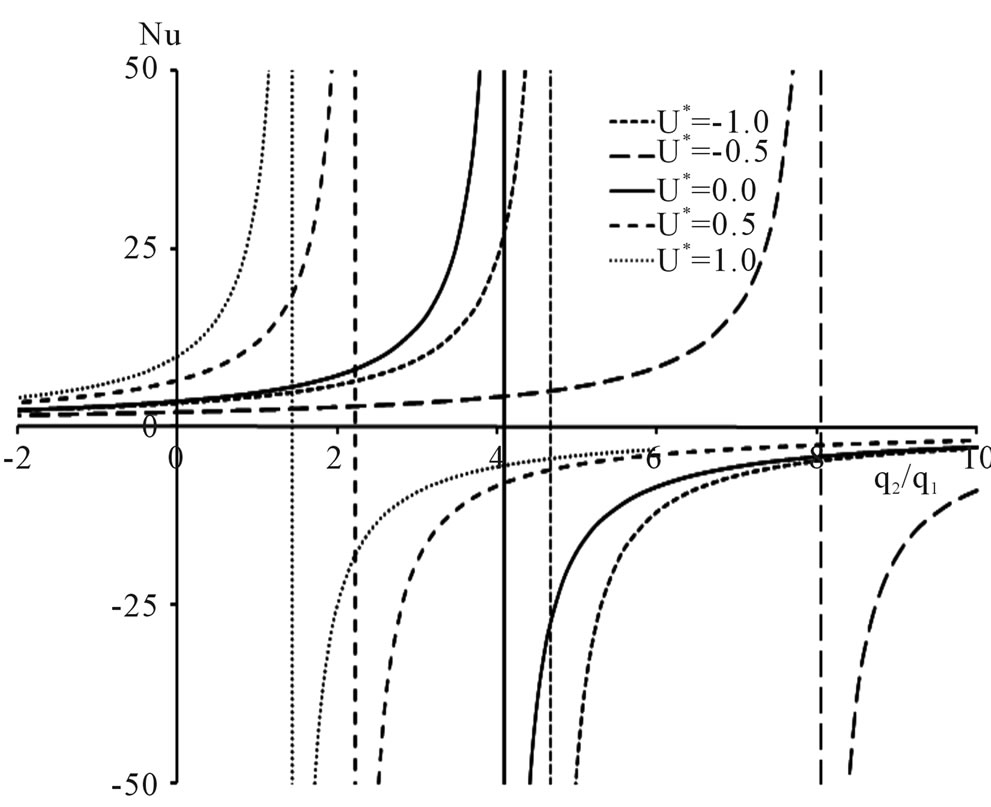 (f)
(f)
Figure 4. Nusselt number versus q2/q1, at U* = −1.0, −0.5, 0.0, 0.5, and 1.0, at various Brq1. Vertical lines are asymptotes. (a) Brq1 = −0.01; (b) Brq1 = −0.10; (c) Brq1 = 0.00; (d) Brq1 = 0.01; (e) Brq1 = 0.10; (f) Brq1 = 0.50.

Table 1. Values of q2/q1 at various Brq1 and U*.
different constant heat fluxes, the dimensionless temperature distribution is given by Equation (15), and the Nusselt number by Equation (22) and they are in terms of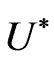 ,
, 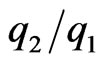 and Various dimensionless velocity values such as −1.0, −0.5, 0.0, 0.5, and 1.0, constant heat flux ratios 0, 0.5, 1.0, 2.0, 10.0 and 50.0 and modified Brinkaman numbers −0.01, −0.1, 0.0, 0.01, and 1.0 are considered in the analysis. The behaviour of the temperature distribution and the Nusselt number against these parameters are discussed. The Brinkman Number, the speed of the moving plate and different values of heat fluxes at both the plates have significant impact in the thermal development.
and Various dimensionless velocity values such as −1.0, −0.5, 0.0, 0.5, and 1.0, constant heat flux ratios 0, 0.5, 1.0, 2.0, 10.0 and 50.0 and modified Brinkaman numbers −0.01, −0.1, 0.0, 0.01, and 1.0 are considered in the analysis. The behaviour of the temperature distribution and the Nusselt number against these parameters are discussed. The Brinkman Number, the speed of the moving plate and different values of heat fluxes at both the plates have significant impact in the thermal development.
5. Acknowledgements
Part of the results was submitted as a conference paper to the 4th International Meeting of Advances in Thermo Fluids (IMAT2011), Melaka, Malaysia.
REFERENCES
- J. Sheela-Francisca and C. P. Tso, “Viscous Dissiption Effects on Parallel Plates with Constant Heat Flux Boundary Conditions,” International Communcations in Heat Mass Transfer, Vol. 36, No. 3, 2009, pp. 249-254. doi:10.1016/j.icheatmasstransfer.2008.11.003
- O. Aydin and M. Avci, “Viscous-Dissipation Effects on the Heat Transfer in a Poiseuille Flow,” Applied Energy, Vol. 83, No. 5, 2006, pp. 495-512. doi:10.1016/j.apenergy.2005.03.003
- J. W. Ou and K. C. Cheng, “Effects of Pressure Work and Viscous Dissipation on Graetz Problem for Gas Flows in Parallel Plate Channels,” Warme-und Stoffubertraggung, Vol. 6, No. 4, 1973, pp. 191-198. doi:10.1007/BF02575264
- C. P. Tso, J. Sheela Francisca and Y.-M. Hung, “Viscous Dissipation Effects of Power-Law Fluid within Parallel Plates with Constant Heat Flues,” Journal of Non-Newtonian Fluid Mechanics, Vol. 165, No. 11-12, 2010, pp. 625-630. doi:10.1016/j.jnnfm.2010.02.023
- D. E. Gray, “The Motion of Viscous Fluids,” Amercan Institute of Physics Handbook, 3rd Edition, Section 3c-2, American Institute of Physics, McGraw-Hill, New York, 1972.
- D. A. Nield, A. V. Kuznetsov and M. Xiong, “Thermally Developing Forced Convection in a Porous Medium: Parallel Plate Channel with Walls at Uniform Temperature, with Axial Conduction and Viscous Dissipation Effects,” International Journal Heat and Mass Transfer, Vol. 46, No. 4, 2003, pp. 643-651. doi:10.1016/S0017-9310(02)00327-7
- Y. M. Hung and C. P. Tso, “Effects of Viscous Disspation on Fully Developed Forced Convection in Porous Media,” International Communications in Heat Mass Transfer, Vol. 36, No. 6, 2009, pp. 597-603. doi:10.1016/j.icheatmasstransfer.2009.03.008
- M. M. Salah El-Din, “Effect of Viscous Dissipation on Fully Developed Combined Convection in a Horizontal Double-Passage Channel,” Heat Mass Transfer, Vol. 38, No. 7-8, 2002, pp. 673-677. doi:10.1007/s002310100255
- O. Aydin, “Effects of Viscous Dissipation on the Heat Transfer in Forced Pipe Flow. Part 1: Both Hydro-Dynamically and Thermally Fully Developed Flow,” Energy Conversion Management, Vol. 46, 2005, pp. 757-769.
- O. Aydin, “Effects of Viscous Dissipation on the Heat Transfer in a Forced Pipe Flow. Part 2: Thermally Developing Flow,” Energy Conversion Management, Vol. 46, No. 18-19, 2005, pp. 3091-3102. doi:10.1016/j.enconman.2005.03.011
- S. H. Hashemabadi, S. Gh. Etemad and J. Thibault, “Forced Convection Heat Transfer of Couette-Poiseuille Flow of Nonlinear Visco-Elastic Fluids between Parallel Plates,” International Journal of Heat and Mass Transfer, Vol. 47, No. 17-18, 2004, pp. 3985-3991. doi:10.1016/j.ijheatmasstransfer.2004.03.026
- F. T. Pinho and P. J. Oliveira, “Analysis of Forced Convection in Pipes And Channels with the Simplified Phan-Thien-Tanner Fluid,” International Journal of Heat and Mass Transfer, Vol. 43, No. 13, 2000, pp. 2273-2287. doi:10.1016/S0017-9310(99)00303-8
- S. H. Hashemabadi, S. Gh. Etemad and J. Thibault, “Mathematical Modeling of Laminar Forced Convection of Simplified Phan-Thien-Tanner (SPTT) Fluid between Moving Parallel Plates,” International Communications in Heat Mass Transfer, Vol. 30, No. 2, 2003, pp. 197-205. doi:10.1016/S0735-1933(03)00030-7
- G. Davaa, T. Shigechi and S. Momoki, “Effect of Viscous Dissipation on Fully Developed Heat Transfer of NonNewtonian Fluids in Plane Laminar Poiseuille-Couette Flow,” International Communications in Heat Mass Transfer, Vol. 31, No. 5, 2004, pp. 663-672. doi:10.1016/S0735-1933(04)00053-3
- O. Aydin and M. Avci, “Laminar Forced Convection with Viscous Dissipation in a Couette-Poiseuille Flow between Parallel Plates,” Applied Energy, Vol. 83, No. 8, 2006, pp. 856-867. doi:10.1016/j.apenergy.2005.08.005
- S. Gh. Etemad, A. S. Majumdar and B. Huang, “Viscous Dissipation Effects in Entrance Region Heat Transfer for a Power Law Fluid Flowing between Parallel Plates,” International Journal of Heat and Fluid Flow, Vol. 15, No. 2, 1994, pp. 122-131. doi:10.1016/0142-727X(94)90066-3
- M. Lewandowska and L. Malinowski, “An Analytcal Solution of the Hyperbolic Heat Conduction Equation for the Case of a Finite Medium Symmetrically Heated on Both Sides,” International Communications in Heat Mass Transfer, Vol. 33, No. 1, 2006, pp. 61-69. doi:10.1016/j.icheatmasstransfer.2005.08.004
- A. Pantokratoras, “Effect of Viscous Dissipation and Pressure Stress Work in Natural Convection along a Vertical Isothermal Plate. New Results,” International Journal of Heat and Mass Transfer, Vol. 46, No. 25, 2003, pp. 4979-4983. doi:10.1016/S0017-9310(03)00321-1
- Y.-L. Chen and K.-Q. Zhu, “Couette-Poiseuille Flow of Bingham Fluids between Two Porous Parallel Plates with Slip Conditions,” Journal of Non-Newtonian Fluid Mechanics, Vol. 153, No. 1, 2008, pp. 1-11. doi:10.1016/j.jnnfm.2007.11.004
- O. Jambal, T. Shigechi, G. Davaa and S. Momoki, “Effects of Viscous Dissipation and Fluid Axial Heat Conduction on Heat Transfer for Non-Newtonian Fluids in Ducts with Uniform Wall Temperature Part I: Parallel Plates and Circular Ducts,” International Communications in Heat Mass Transfer, Vol. 32, No. 9, 2005, pp. 1165-1173. doi:10.1016/j.icheatmasstransfer.2005.07.002
- K. C. Cheng and R. S. Wu, “Viscous Dissipation Effects on Convective Instability and Heat Transfer in Plane Poiseuille Flow Heated from Below,” Applied Science Research, Vol. 32, No. 4, 1976, pp. 327-346.
- B. Li, L. Zheng and X. Zhang, “Heat Transfer in Pseudo-Plastic Non-Newtonian Fluids with Variable Thermal Conductivity,” Energy Conversion Management, Vol. 52, No. 1, 2011, pp. 355-358. doi:10.1016/j.enconman.2010.07.008
- W. M. Kays, “Convective Heat and Mass Transfer,” 4th Edition, McGraw-Hill, New York, 1966, p. 104.

