Open Journal of Fluid Dynamics
Vol.2 No.4A(2012), Article ID:25788,6 pages DOI:10.4236/ojfd.2012.24A019
Effects of Supersonic Nozzle Geometry on Characteristics of Shock Wave Structure
1Department of Advanced Technology Fusion, Saga University, Saga, Japan
2Graduate School of Science & Engineering, Saga University, Saga, Japan
3Institute of Ocean Energy, Saga University, Saga, Japan
4School of Mechanical Engineering, Andong National University, Andong, South Korea
Email: *matsuo@me.saga-u.ac.jp
Received September 1, 2012; revised October 3, 2012; accepted October 16, 2012
Keywords: Compressible Flow; Asymmetric Shock Wave; Supersonic Nozzle; Experiment
ABSTRACT
Interaction between the normal shock wave and the turbulent boundary layer in a supersonic nozzle becomes complex with an increase of a Mach number just before the shock wave. When the shock wave is strong enough to separate the boundary layer, the shock wave is bifurcated, and the 2nd and 3rd shock waves are formed downstream of the shock wave. The effect of a series of shock waves thus formed, called shock train, is considered to be similar to the effect of one normal shock wave, and the shock train is called pseudo-shock wave. There are many researches on the configuration of the shock wave. However, so far, very few researches have been done on the asymmetric characteristics of the leading shock wave in supersonic nozzles. In the present study, the effect of nozzle geometry on asymmetric shock wave in supersonic nozzles has been investigated experimentally.
1. Introduction
The supersonic flow fields with the pseudo-shock wave are observed in some apparatuses, such as the separation part of a SCRAM jet engine, a high pressure gas piping system, supersonic diffuser and so on.
In the supersonic internal flow, interaction between the shock wave and the boundary layer is very complex and induces the separation of boundary layer. When the shock wave is strong enough to separate the boundary layer, the shock wave is bifurcated and more shock waves are formed downstream of the leading shock wave. The series of shock waves are called shock train. This shock train and the resulting mixing region construct a pseudo-shock wave [1], which plays a role similar to that of a single normal shock wave. The leading shock wave of the pseudo-shock wave is classified into λ-type and X-type shock waves by Mach number or Reynolds number.
Neumann and Lustwerk [2] indicated that static pressure on the wall increased monotonously, and the length of the pseudo-shock wave, defined as the distance from the starting point of the pressure rise to point of the maximum pressure, was 8 - 13 times the duct diameter.
Tamaki et al. [3,4] reported that with an increase of the main flow Mach number, the configuration of the pseudo-shock wave changed from λ-type shock wave to X-type shock wave and the range of the shock wave was expanded. However, the asymmetric characteristics of the leading shock wave have not been investigated satisfactorily.
Numerical and experimental researches on the symmetric and asymmetric shock wave system in a planar nozzle were presented by Xiao et al. [5] and Papamoschou et al. [6-8]. Papamoschou et al. [6,7] revealed that either of two distinct systems is occurred depending on area ratio (cross-sectional area at the nozzle exit to crosssectional area at the nozzle throat). One is the symmetrical λ-type shock wave system and the other is the asymmetrical separation with lager λ-type foot. Thus, some researches have been done on the effect of the area ratio on asymmetric characteristics of the leading shock wave in supersonic nozzles. However, there are few researches for the effects of nozzle length and nozzle throat on the characteristics.
The purpose of this study is to investigate the effects of the nozzle length with parallel part and the position of nozzle throat on the characteristics of asymmetric shock wave in supersonic nozzles experimentally.
2. Experimental Apparatus and Method
2.1. Experimental Apparatus
Figure 1 shows a schematic diagram of the experimental apparatus. The apparatus is consisted of compressor, air drier, air reservoir, electronic control valve, plenum chamber and nozzle. Plenum chamber is placed upstream of the supersonic nozzle. Compressed dry air was used as a working gas. Optical glass windows are installed on both the side walls of the test section for flow visualization.
Figure 2 shows the detail of nozzle configuration used in the present study. The nozzle is a supersonic nozzle with a straight part. Symbol c indicates the displacement distance of lower wall (upper wall is fixed) and the position corresponding to c = 0 means the position which height from nozzle centerline to each wall (upper and lower walls) is the minimum, that is, the position of nozzle throat. L1 for the upper wall is constant (L1 = 54.6 mm). The depth of test section is 33.9 mm.
Table 1 shows dimensions of each nozzle. The nozzle of BN is standard one and the asymmetric leading shock wave is obtained by the nozzle (Mach number at the nozzle exit: 2.06) that was designed based on Ref. [6,7]. Lengths of parallel parts for EN-11 and EN-55 are 1Dt and 5Dt, respectively. The lower walls for ND-0.2 and ND-1.0 are displaced downstream compared with that of standard nozzle (BN) by 0.2 mm and 1.0 mm, respectively. For NU-0.2 and NU-1.0, the lower wall is displaced upstream compared with that of BN by 0.2 mm and 1.0 mm, respectively.
2.2. Experimental Procedure
In the present experiments, pressure ratio  was continuously changed with time using the electronic control valve. The symbol, p0 and pb represent the stagnation pressure of the plenum chamber and back pressure (atmospheric pressure), respectively. The range of
was continuously changed with time using the electronic control valve. The symbol, p0 and pb represent the stagnation pressure of the plenum chamber and back pressure (atmospheric pressure), respectively. The range of 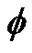 is from 1.9 to 3.4. The rate of the change of pressure ratio with time is 0.083 (1/s).
is from 1.9 to 3.4. The rate of the change of pressure ratio with time is 0.083 (1/s).
Compressed dry air is discharged from nozzle exit through the plenum chamber. The flow field was investigated by a schlieren optical method. Visualization and measurement of pressure ratio were conducted simultaneously. The location of the leading shock wave L was obtained from schlieren pictures.
3. Computational Analysis
Numerical Methods
Numerical simulations were conducted using the FLUENT software (Version 6.3) in order to investigate the flow characteristics in the range close to a part of the minimum cross-sectional area in the nozzle, some numerical simulations were conducted.
The governing equations are mass averaged, time-dependent compressible Navier-Stokes equations. The resulting equations are expressed in an integral from:
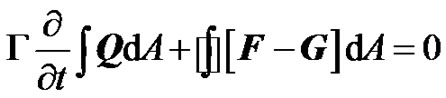 (1)
(1)
where F and G are the inviscid and viscous flux vectors in standard conservation form and Q is the dependent vector of primary variables.
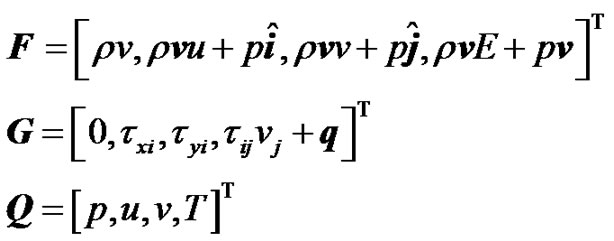 (2)
(2)
where v is the velocity vector. 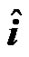 and
and 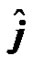 are unit vectors of x and y directions, respectively.
are unit vectors of x and y directions, respectively.
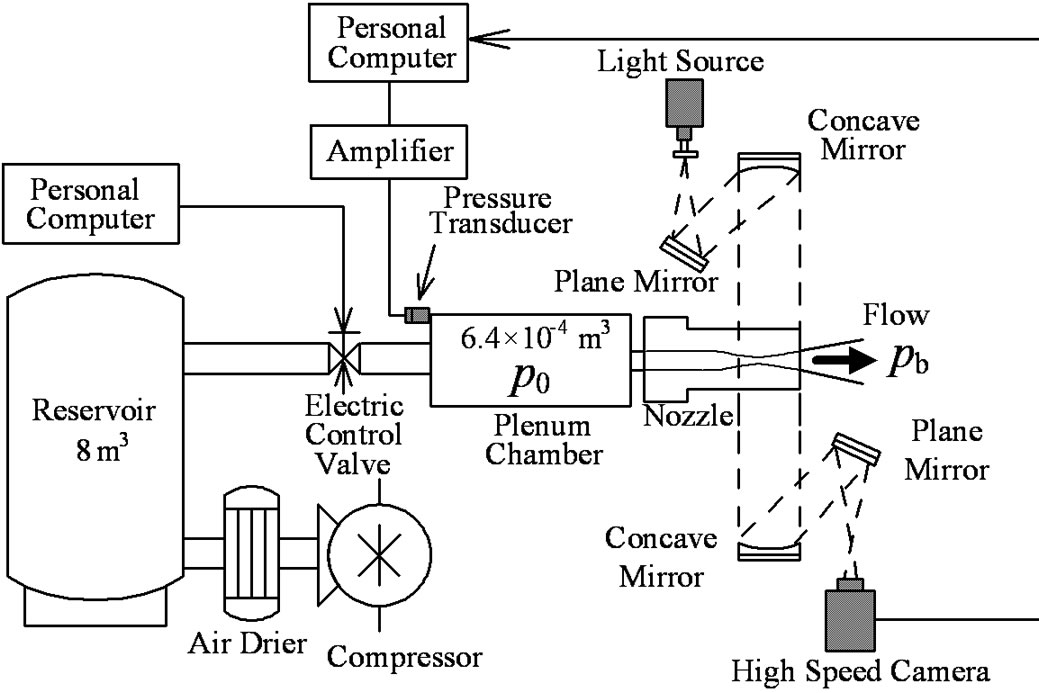
Figure 1. Experimental apparatus.
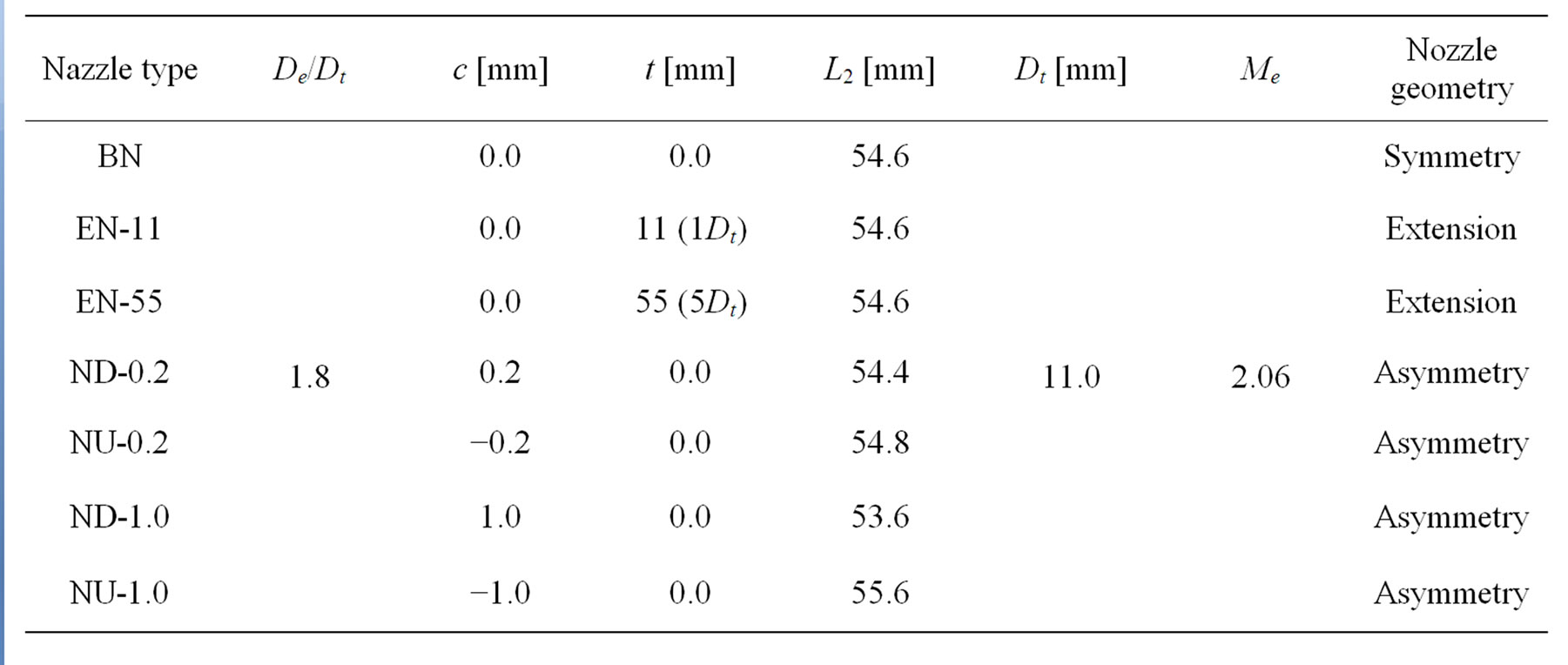
Table 1. Nozzle configurations.
In the above equations, H is total enthalpy per unit mass and is related to the total energy E by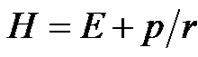 , where E includes both internal and kinetic energies. The preconditioning matrix
, where E includes both internal and kinetic energies. The preconditioning matrix 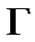 is included in Equation (1) to provide an efficient solution of the present axisymmetric compressible flow. This matrix is given by
is included in Equation (1) to provide an efficient solution of the present axisymmetric compressible flow. This matrix is given by
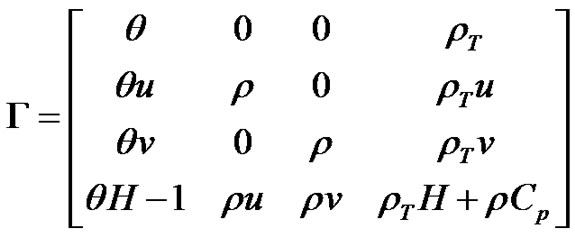 (3)
(3)
where 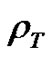 is the derivative of density with respect to temperature at constant pressure. The parameter
is the derivative of density with respect to temperature at constant pressure. The parameter 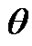 is defined as
is defined as
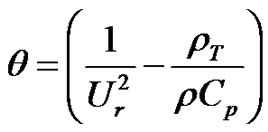 (4)
(4)
In Equation (4), the reference velocity Ur is chosen such that the eigenvalues of the system remain well conditioned with respect to the convective and diffusive timescales and Cp is the specific heat at constant pressure.
The preconditioned governing equations [9] are discretized spatially using a finite volume scheme. For the time derivatives, an implicit multistage time stepping scheme which is advanced from time t to time t + Dt with a 2nd order Euler backward scheme for physical time and implicit pseudo-time marching scheme for inner iteration, is used. To close the governing equations, k-ω SST (Shear-Stress Transport) turbulent model [10-12] was employed in computations.
The computational domain and boundary conditions are illustrated in Figure 3" target="_self"> Figure 3. The boundary conditions are the inlet total pressure and the outlet static pressure, respectively. The adiabatic no-slip conditions are applied to the solid walls. A structured clustered grid system was employed in the computations. A solution convergence was obtained when the residuals for each of the conserved variables were reduced below the order of magni-
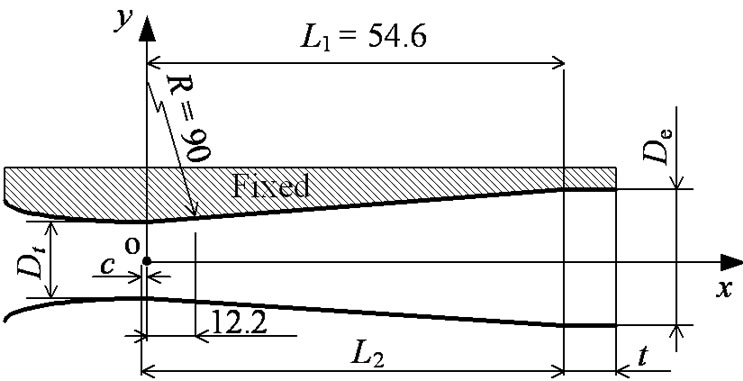
Figure 2. Nozzle geometry.
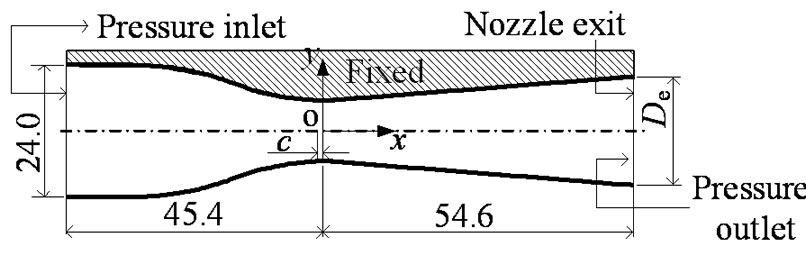
Figure 3. Schematic view of computational domain and boundary conditions (Unit: mm).
tude 4. The net mass flux was investigated when there was an applicable imbalance through the computational boundaries.
4. Results and Discussions
Figure 4 shows schlieren photographs of the flow field in a supersonic nozzle. The white arrows in the figure are pointing to the leading shock wave. In this figure, the configuration of the leading shock wave in the nozzle forms λ-type shock wave or X-type shock wave in each nozzle and it is found that the configuration of the shock wave has asymmetry to the nozzle axis.
Figure 5 shows relationship between pressure ratio and difference (absolute value) between distances from triple points to upper and lower walls 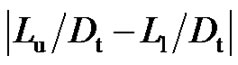 for BN, EN-11 and EN-55. From this figure, it is found that the difference is the largest for BN and the asymmetric characteristics in the nozzle become smaller with an increase of length of the nozzle straight part. The
for BN, EN-11 and EN-55. From this figure, it is found that the difference is the largest for BN and the asymmetric characteristics in the nozzle become smaller with an increase of length of the nozzle straight part. The

Figure 4. Schlieren photographs. (a) BN; (b) EN-11; (c) EN-55; (d) ND-0.2; (e) ND-1.0; (f) NU-0.2; (g) NU-1.0.
cause of the result is considered that the influence of propagation of pressure disturbances from downstream of the nozzle exit is weakened.
Figure 6 shows the relationship between pressure ratio and difference of distances from triple points to upper and lower walls for 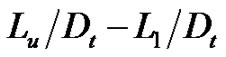 of BN, ND-0.2, ND-1.0, NU-0.2 and NU-1.0. As seen from Figure 6, the asymmetry decreases with an increase of pressure ratio for ND-0.2, ND-1.0, NU-0.2 and NU-1.0, and distance from triple point of upper wall side becomes larger than that of lower wall side in cases of BN, ND-0.2 and ND-1.0. On the other hand, in cases of NU-0.2 and NU-1.0, distance from triple point of upper wall side becomes smaller than that of lower wall side.
of BN, ND-0.2, ND-1.0, NU-0.2 and NU-1.0. As seen from Figure 6, the asymmetry decreases with an increase of pressure ratio for ND-0.2, ND-1.0, NU-0.2 and NU-1.0, and distance from triple point of upper wall side becomes larger than that of lower wall side in cases of BN, ND-0.2 and ND-1.0. On the other hand, in cases of NU-0.2 and NU-1.0, distance from triple point of upper wall side becomes smaller than that of lower wall side.
In Figure 6, value of 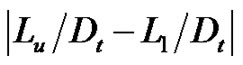 becomes large with an increase of displacement distance except the case of NU-02. This means the increase of the asymmetry. In order to investigate the cause of the results, numerical simulations were conducted in the range close to a part of the minimum cross-sectional area in the nozzle.
becomes large with an increase of displacement distance except the case of NU-02. This means the increase of the asymmetry. In order to investigate the cause of the results, numerical simulations were conducted in the range close to a part of the minimum cross-sectional area in the nozzle.
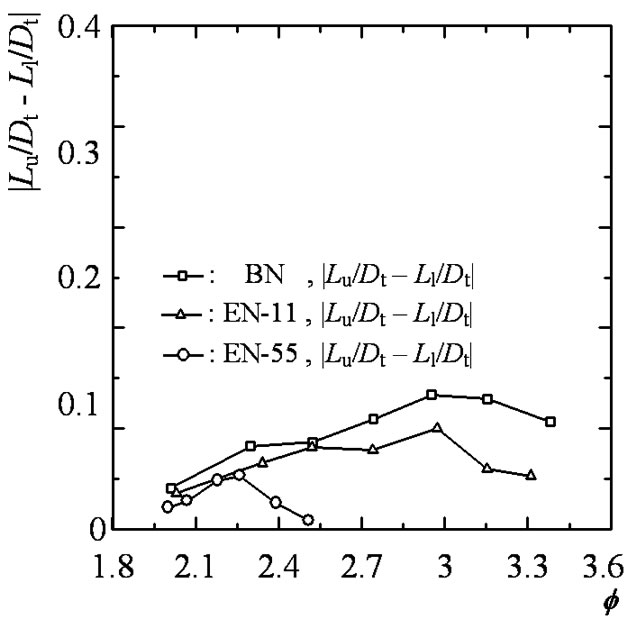
Figure 5. Distance from triple point to upper and lower walls (BN, EN-11, EN-55).

Figure 6. Distance from triple point to upper and lower walls (BN, ND, NU).
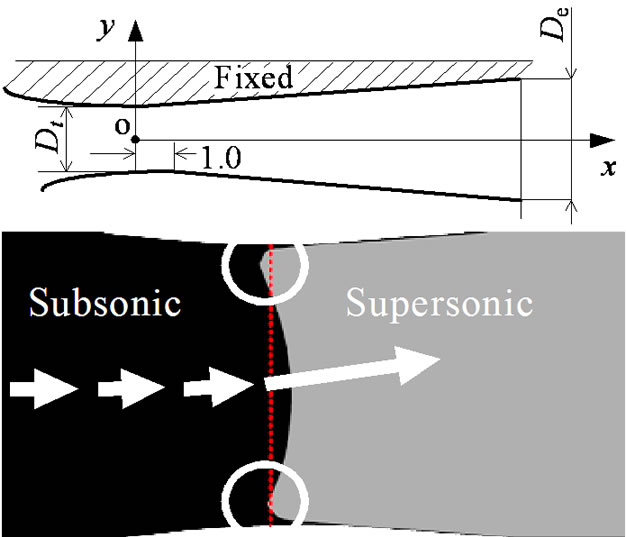
Figures 7(a) and (b) show schematic diagrams of the sonic line for ND-1.0 and NU-1.0, respectively. Dashed lines indicate the throat position in case of c = 0 (BN). In Figure 7(a), it seems that the sonic line at upper wall side exists upstream compared with that of lower wall side. As a result, the flow is directed towards the upper wall side and Mach number just before the shock wave at the upper wall side becomes larger compared with that in the case of BN. Therefore, value of 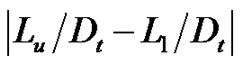 becomes larger by interacting strongly with the boundary layer. In Figure 7(b), it seems that the sonic line at lower wall side exists upstream compared with that of upper wall side and the flow is directed towards the lower wall side. As a result, value of
becomes larger by interacting strongly with the boundary layer. In Figure 7(b), it seems that the sonic line at lower wall side exists upstream compared with that of upper wall side and the flow is directed towards the lower wall side. As a result, value of 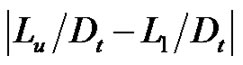 becomes larger for
becomes larger for 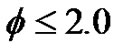 in the same manner as the case in Figure 7(a).
in the same manner as the case in Figure 7(a).
Figure 8 shows the relationship between pressure ratio and difference (absolute value) of distances from triple points to upper and lower walls 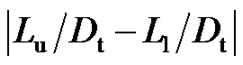 for BN, NU-0.2 and NU-1.0. For
for BN, NU-0.2 and NU-1.0. For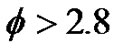 , asymmetry of shock wave becomes weak in case of NU-0.2 compared with those of BN and NU-1.0. As seen from this figure, the asymmetry is effectively reduced by displacing slightly the lower wall into upstream in the range of high pressure ratio.
, asymmetry of shock wave becomes weak in case of NU-0.2 compared with those of BN and NU-1.0. As seen from this figure, the asymmetry is effectively reduced by displacing slightly the lower wall into upstream in the range of high pressure ratio.
 (a)
(a)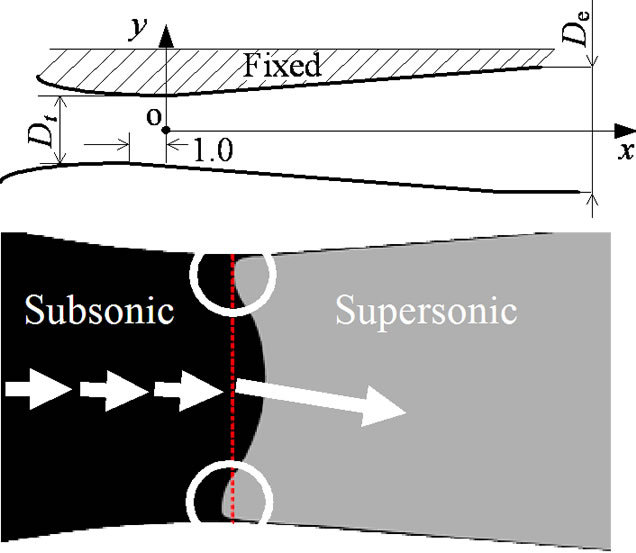 (b)
(b)
Figure 7. Sonic lines. (a) ND-1.0; (b) NU-1.0.
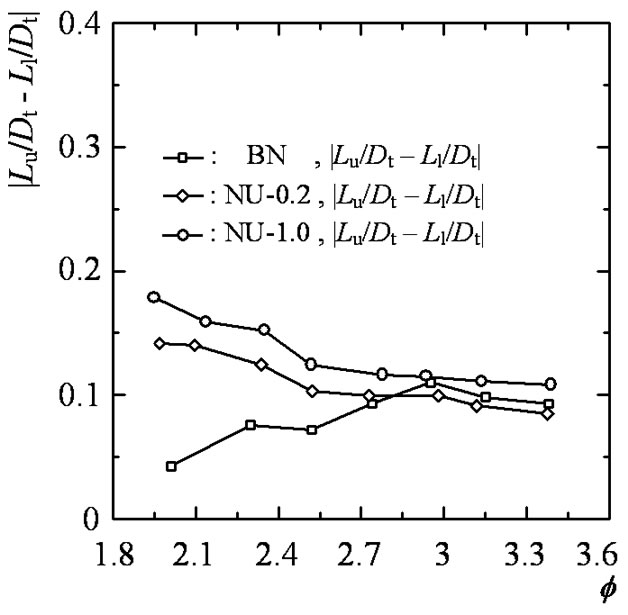
Figure 8. Distance from triple point to upper and lower walls (BN, NU-0.2, NU-1.0).
5. Conclusions
In the present study, the effects of nozzle geometry on the asymmetry of shock wave were experimentally investigated using 7 kinds of supersonic nozzle. The results obtained are summarized as follow:
1) The asymmetry of the shock wave became small with an increase of length of the nozzle straight part;
2) When the lower wall was displaced, the asymmetry of the shock wave became small with an increase in pressure ratio.
The asymmetry might be effectively reduced by moving the lower wall to a suitable position.
REFERENCES
- K. Matsuo, Y. Miyazato and H. D. Kim, “Shock Train and Pseudo-Shock Phenomena in Internal Gas Flows,” Progress in Aerospace Sciences, Vol. 35, No. 1, 1999, pp. 33-100. doi:10.1016/S0376-0421(98)00011-6
- E. P. Neumann and F. Lustwerk, “Supersonic Diffusers for Wind Tunnels,” Journal of Applied Mechanics, Vol. 16, No. 2, 1949, pp. 195-202.
- T. Tamaki, Y. Tomita and R. Yamane, “A Research on Pseudo-Shock (1st Report, λ-Type Pseudo-Shock),” Bulletin of JSME, Vol. 13, No. 55, 1970, pp. 191-226.
- T. Tamaki, Y. Tomita and R. Yamane, “A Research on Pseudo-Shock (2nd Report, X-Type Pseudo-Shock),” Bulletin of JSME, Vol. 14, No. 74, 1971, pp. 807-817.
- Q. Xiao, H. M. Tsai and D. Papamoschou, “Numerical Investigation of Supersonic Nozzle Flow Separation,” AIAA Journal, Vol. 45, No. 3, 2007, pp. 532-541. doi:10.2514/1.20073
- D. Papamoschou and A. Zill, “Fundamental Investigation of Supersonic Nozzle Flow Separation,” American Institute of Aeronautics and Astronautics, Inc., Reston, 2004.
- D. Papamoschou, A. Zill and A. Johnson, “Supersonic Flow Separation in Planar Nozzles,” Shock Waves, Vol. 19, No. 3, 2006, pp. 171-183. doi:10.1007/s00193-008-0160-z
- D. Papamoschou and A. Johnson, “Unsteady Phenomena in Supersonic Nozzle Flow Separation,” American Institute of Aeronautics and Astronautics, Inc., Reston, 2006.
- J. M. Weiss and W. A. Smith, “Preconditioning Applied to Variable and Constant Density Flows,” AIAA Journal, Vol. 33, No. 11, 1995, pp. 2050-2057. doi:10.2514/3.12946
- F. R. Menter, “Zonal Two Equation k-ω Turbulence Models for Aerodynamic Flows,” American Institute of Aeronautics and Astronautics, Inc., Reston, 1993.
- F. R. Menter, “Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications,” AIAA Journal, Vol. 32, No. 8, 1994, pp. 269-289. doi:10.2514/3.12149
- F. R. Menter, M. Kuntz and R. Langtry, “Ten Years of Industrial Experience with the SST Turbulence Model,” Proceedings of the 4th International Symposium on Turbulence, Heat and Mass Transfer, Begell House Inc., West Redding, 2003, pp. 625-632.
NOTES
*Corresponding author.

