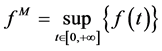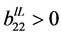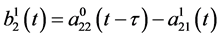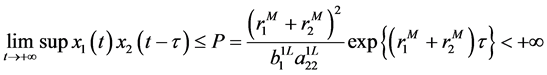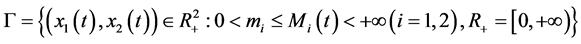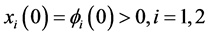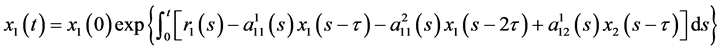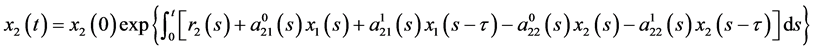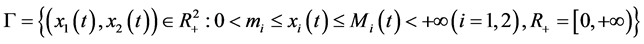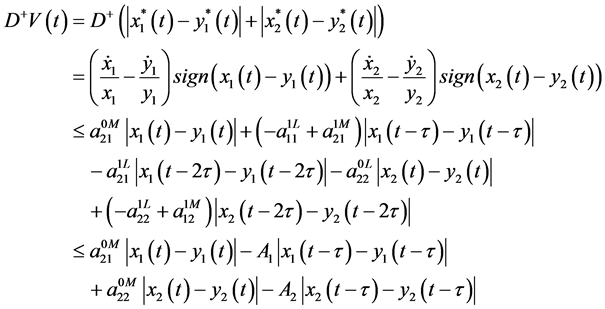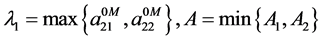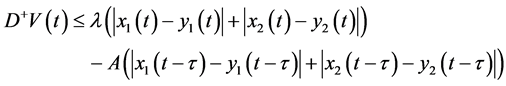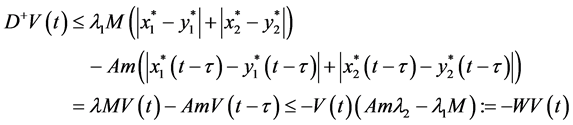Open Journal of Applied Sciences
Vol.07 No.05(2017), Article ID:76704,6 pages
10.4236/ojapps.2017.75018
Global Stability for a Asymptotically Periodic Cooperative Lotka-Volterra System with Time Delays
Talat Tayir, Rouzimaimaiti Mahemuti
College of Mathematics and System Sciences, Xinjiang University, Urumqi, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 20, 2017; Accepted: May 28, 2017; Published: May 31, 2017
ABSTRACT
In this paper a class of cooperative Lotka-Volterra population system with time delay is considered. Some sufficient conditions on the existence and globally asymptotically stability for the asymptotically periodic solution of the system are established by using the Lyapunov function method and the method given in Fengying Wei and Wang Ke (Applied Mathematics and Computation 182 (2006) 161-165).
Keywords:
Lotka-Volterra Cooperative System, Asymptotically Periodic Function, Global Asymptotic Stability, Time Delay

1. Introduction
Since Lotka-Volterra system has been established and was accepted by many scientists, it becomes the most important means to explain the ecological phenomenon now. For many years, a lot of extensive research results were made in mathematical biology and mathematical ecology [1] - [8] , during this time Lotka- Volterra system has played an important role in theses research field of mathematical biology and mathematical ecology. Still now many research work mostly discussed periodic Lotka-Volterra systems [2] [3] [4] [5] [6] and the references cited therein. In fact asymptotically periodic systems [3] [4] describe our world more realistic and more accurate than periodic ones.
As is well known, Lotka-Volterra Cooperative system is one of the most important classe of interaction model which is discussed widely in mathematical biology and mathematical ecology.
In this paper we consider the following Lotka-Volterra cooperative system with time delay:
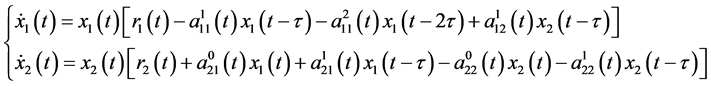 (1)
(1)
where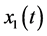 ,
,  are the density of two cooperative species at time t respectively,
are the density of two cooperative species at time t respectively, 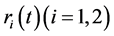 are intrinsic growth rate of two cooperative species at time t respectively,
are intrinsic growth rate of two cooperative species at time t respectively,  ,
, 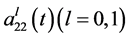 are the intra patch restriction density of species
are the intra patch restriction density of species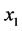 ,
, 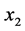 , at time t respectively, and
, at time t respectively, and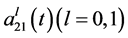 ,
, 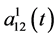 are the are cooperative coefficients between two species at time t respectively. In this paper we assume that system (1) satisfies the following assumption
are the are cooperative coefficients between two species at time t respectively. In this paper we assume that system (1) satisfies the following assumption
(H1)  is a positive constant and
is a positive constant and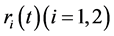 ,
,  ,
, 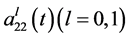 ,
, 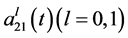 and
and 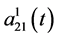 are continuous, asymptotically periodic, bounded and strictly positive functions on
are continuous, asymptotically periodic, bounded and strictly positive functions on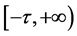 .
.
From the viewpoint of mathematical biology, in this paper, for system (1) we consider the solution with the following initial condition
 (2)
(2)
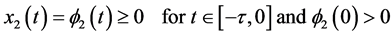
then for any
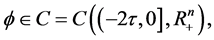
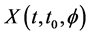
For a continuous and bounded function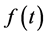
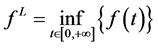
Y. Nakata and Y. Muroya have proved in [1] that the system (1) is permanent under the following conditions
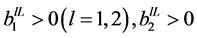
where
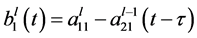
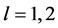
which means that the system (1) had a bounded region that is
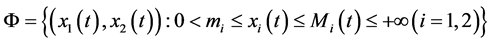
In particularly,
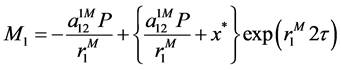
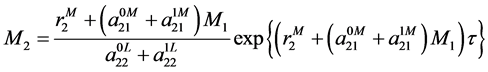
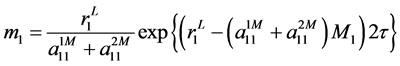
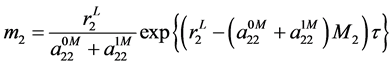
where 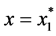
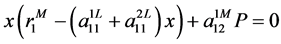
Let the set
where 
Following is the adjoin system (2) of system (1)
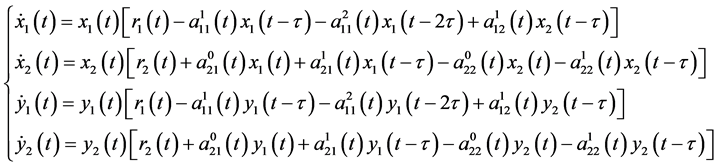
Now, we present a useful definition
Definition 1.1 (see [ [3] Definition 1.1]) 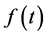
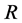
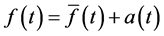
where 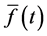
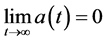
Now, we present some useful lemmas.
Lemma 2.1 The set 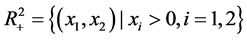
Proof. We can obtain for
our results will be discussed in the positively invariant set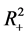
Let the set
where 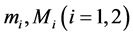
Lemma 2.2 Assume that 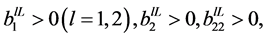
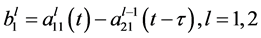
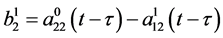
Lemma 2.3 ( [4] ) Let 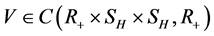
1)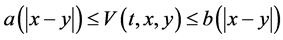
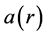
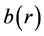
2)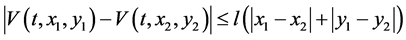
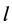
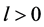
3) There exists continuous function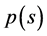
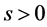
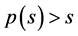
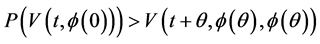
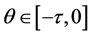
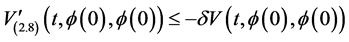
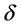
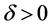
Furthermore, system (2.7) has a solution 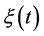
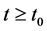
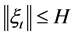
Our main purpose is to establish some sufficient conditions on the existence and globally asymptotically stability for the asymptotically periodic solution of the system (1). The method used in this paper is motivated by the work done by Fengying Wei and Wang Ke in [4] and the Lyapunov function method.
2. Main Results
Theorem 2.1 Assume that the condition of lemma 2.2 is hold and 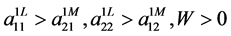
Proof. From Lemma 2.2, we know that the solution of system (1) is ultimately bounded. 
For 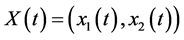
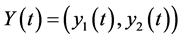
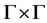
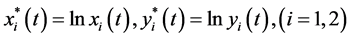
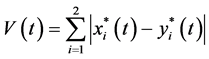
Take 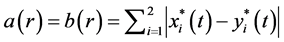
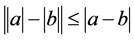
where 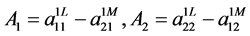
Then we have
By the following formula:
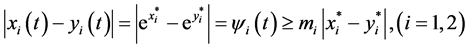
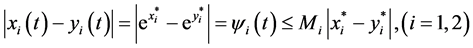
where 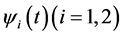
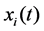
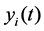
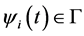
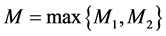
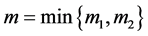
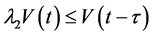
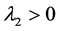
where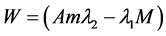
From the known condition of Theorem 2.1, we obtain that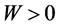
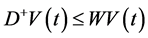
3. Conclusions
In [1] the author’s discussed system (1) and derived some sufficient conditions on the permanence of system (1). However, in this paper, based on the permanence of the system (1), we further study system (1) in a asymptotically periodic environment and established conditions on the existence and globally asymptotically stability for the asymptotically periodic solution of the system (1) by using the Lyapunov function method and the method given in Fengying Wei and Wang Ke (Applied Mathematics and Computation 182 (2006) 161 - 165).
We have more interesting topics deserve further investigation, such as the dynamical behaviors of n-species Lotka-Volterra cooperative systems with discrete time delays.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11401509).
Cite this paper
Tayir, T. and Mahemuti, R. (2017) Global Stability for a Asymptotically Periodic Cooperative Lotka- Volterra System with Time Delays. Open Journal of Applied Sciences, 7, 207-212. https://doi.org/10.4236/ojapps.2017.75018
References
- 1. Nakata, Y. and Muroya, Y. (2010) Permanence for Nonautonomous Lotka-Volterra Cooperative Systems with Delays. Nonlinear Analysis: Real World Applications, 11, 528-534.
- 2. Lu, S. (2008) On the Existence of Positive Periodic Solutions to a Lotka Volterra Cooperative Population Model with Multiple Delays. Nonlinear Analysis: Theory, Methods & Applications, 68, 1746-1753.
- 3. Wei, F. and Wang, K. (2006) Asymptotically Periodic Solution of N-Species Cooperation System with Time Delay. Nonlinear Analysis: Real World Applications, 7, 591-596.
- 4. Wei, F. and Wang, K. (2006) Global Stability and Asymptotically Periodic Solution for Nonautonomous Cooperative Lotka-Volterra Diffusion System. Applied Mathematics and Computation, 182, 161-165.
- 5. Wei, F. and Wang, K. (2002) Almost Periodic Solution and Stability for Nonautonmous Cooperative Lotka-Volterra Diffusion System. Songliao Journal (Natural Science Edition), 3.
- 6. Liu, C. and Chen, L. (1997) Periodic Solution and Global Stability for Nonautonomous Cooperative Lotka-Volterra Diffusion System. Journal of Lanzhou University (Natural Science), 33, 33-37.
- 7. Zhang, J. and Chen, L. (1996) Permanence and Global Stability for Two-Species Co-Operative System with Delays in Two-Patch Environment. Mathematical and Computer Modelling, 23, 17-27.
- 8. Chen, F. (2003) Persistence and Global Stability for Nonautonomous Co-Operative System with Diffusion and Time Delay. Acta Scientiarum Naturalium Universitatis Pekinensis, 39, 22-28.