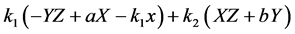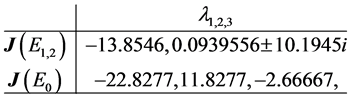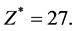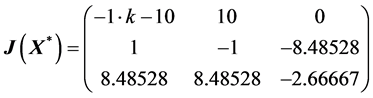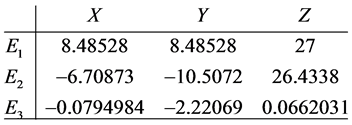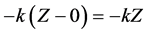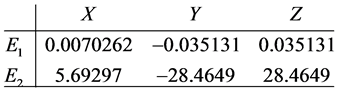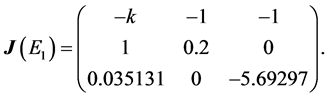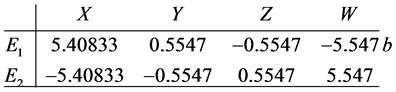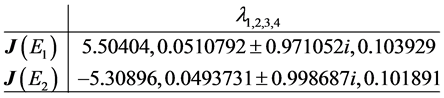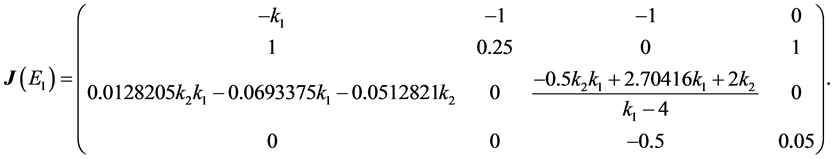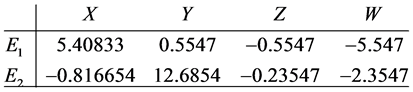Open Journal of Applied Sciences
Vol.06 No.03(2016), Article ID:64565,12 pages
10.4236/ojapps.2016.63015
Applying Linear Controls to Chaotic Continuous Dynamical Systems
James Braselton, Yan Wu
Department of Mathematical Sciences, Georgia Southern University, Statesboro, GA, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 January 2016; accepted 13 March 2016; published 16 March 2016
ABSTRACT
In this case-study, we examine the effects of linear control on continuous dynamical systems that exhibit chaotic behavior using the symbolic computer algebra system Mathematica. Stabilizing (or controlling) higher-dimensional chaotic dynamical systems is generally a difficult problem, Musielak and Musielak, [1] . We numerically illustrate that sometimes elementary approaches can yield the desired numerical results with two different continuous higher order dynamical systems that exhibit chaotic behavior, the Lorenz equations and the Rössler attractor.
Keywords:
Chaotic Dynamical System, Lorenz Equations, Rössler Attractor, Chaos, Hyperchaos, Control, Stability, Routh-Hurwitz Theorem, Characteristic Polynomial

1. Introduction
We begin with an autonomous continuous dynamical system , where
, where 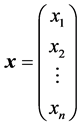 and
and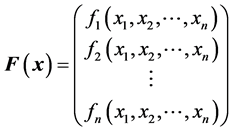 .
.
We use the notation that  is a rest point, or equilibrium point of
is a rest point, or equilibrium point of , if
, if .
.
Under some parameter values or initial conditions, the system  exhibits chaos or hyperchaos. Refer to Yu et al., [2] , for a discussion regarding the differences between chaos and hyperchaos.
exhibits chaos or hyperchaos. Refer to Yu et al., [2] , for a discussion regarding the differences between chaos and hyperchaos.
Control theory attempts to find a controller to apply to the dynamical system that stabilizes the system and eliminates the chaos or hyperchaos. In the context of the autonomous dynamical system , the investigator searches for a function
, the investigator searches for a function  so that
so that  does not exhibit chaos or hyperchaos for the given parameter values and initial conditions that the original system,
does not exhibit chaos or hyperchaos for the given parameter values and initial conditions that the original system, 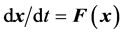 exhibits using those parameter values and initial conditions.
exhibits using those parameter values and initial conditions.
The focus of this paper is to illustrate an automated technique to find a linear control ( ) of a continuous dynamical system that exhibits chaos or hyperchaos. In subsequent studies, we will focus both on the controller design, conditions when a chaotic system is stabilized, and the physical interpretation of the controller for specific dynamical systems.
) of a continuous dynamical system that exhibits chaos or hyperchaos. In subsequent studies, we will focus both on the controller design, conditions when a chaotic system is stabilized, and the physical interpretation of the controller for specific dynamical systems.
2. Background
Li and Li, [3] , provide examples of several approaches to controlling the chaotic three dimensional Chen-Lee system in their paper and illustrate how different multiple control techniques stabilize the system in their case study. To briefly summarize their results, Li and Li, [3] , provide several approaches to control and provide synchronization of the chaotic Chen-Lee System,
 (1)
(1)
at the origin, . In their case study they use three feedback controls that are summarized as follows.
. In their case study they use three feedback controls that are summarized as follows.
(1) Linear Feedback Control. Linear ,
, 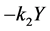
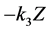
(2) Speed Feedback Control. A single control of the form
is incorporated into the x-equation of system (1). 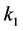
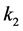
(3) Doubly-Periodic Function Feedback Control. The control in the X-equation is 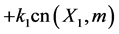
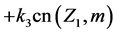
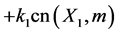

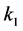

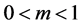
The form of the design used to attempt to control a given system can be motivated by many factors. In general, controlling nonlinear high-dimensional chaotic dynamical systems can be a formidable problem, Musielak and Musielak, [1] . Viera and Lichtenberg, [5] , illustrate several examples of controlling chaos using a nonlinear feedback with delay. On the other hand, Tan et al., [4] , develop a controller using a backstopping design.
In this paper, we demonstrate a sequence of algorithms that may be used to find a linear control for a high- dimensional non-linear dynamical system that exhibits chaos or hyperchaos under certain conditions. We show
that a basic linear control of the form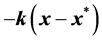
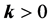
sional non-linear chaotic dynamical systems provided that the underlying parameter values are known a priori.
We use a computer algebra system like Mathematica or Maple to implement the procedure to find the simplest linear control, when possible. In this paper, we use Mathematica. The technique is described next.
(1) Begin with an autonomous continuous dynamical system, 
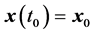
(2) Assume that the appropriate parameter values and initial conditions are known and the system exhibits chaos or hyperchaos at an equilibrium point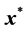
(3) Based on the known parameter values investigate a proportional controllerl of the form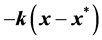
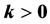
(4) If it is possible to find a proportional controller using the given constraints, the problem is solved.
(a) Linearize the controlled system 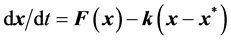
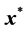
(b) Compute the Jacobian, 
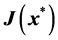
(i) Obtain bounds on the real part of 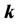
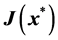
or
(ii) Compute the eigenvalues of 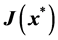
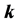
the real part of all eigenvalue is negative, if possible. Remark: Our simulations indicate that this yields better results than the Routh-Hurwitz theorem when the maximum value of the real part of the eigenvalues is close to 0.
(A) Given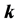
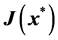
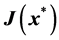
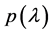
(B) Find the real part of all zeros of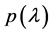
(C) Find conditions on 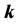
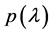
(5) Underlying Strategy: The “best” control is the simplest one. Thus, we start by searching for the simplest linear control possible.
For our case-studies we choose to numerically illustrate the techniques on versions of the Lorenz equations and Rössler attractors because they are well studied and because of their broad use in applications. Of course, a similar analysis can be carried out with many other high-dimensional dynamical systems that exhibit chaotic behavior, which we hope to do in future studies where we will focus on the underlying physical interpretation of the control.
3. The Lorenz Equations
The Lorenz system is a three-dimensional continuous nonlinear dynamical system,
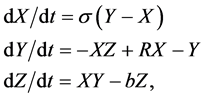
that has numerous applications in areas such as simple models of lasers, thermosyphons, and some chemical reactions.
Parameter 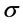
For example, Figure 1 illustrates chaos in the Lorenz system using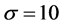
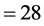
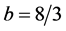
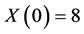
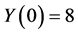

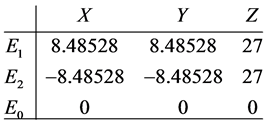
Figure 1. Chaos in the Lorenz system using “typical” parameter values. The initial conditions are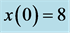
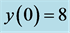
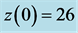
The Jacobian of system (2) evaluated at each equilibrium point has the following eigenvalues
which shows that all three equilibrium points are unstable.
Using the described algorithm to try to find a control for an unstable equilibrium point, we choose an equilibrium point and search for the simplest control possible to stabilize it. To illustrate the concept, we choose
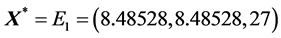
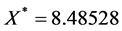
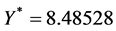
3.1. X-Control
We attempt to find the simplest control possible so search for an initial control of the form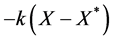

Evaluated at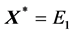
which has characteristic equation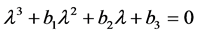
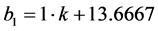

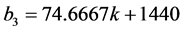
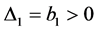
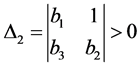
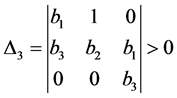

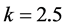
With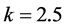
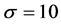
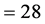
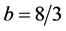
Figure 2. Stabilizing 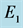
The Jacobian of system (3) evaluated at each equilibrium point has the following eigenvalues
Observe that the Jacobian confirms that 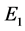
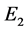
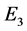
This algorithm is well-suited to computer arithmetic and can be carried out at other equilibria. For example, rather than
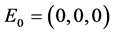
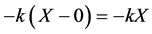

3.2. Y-Control
Generally, smaller k-values are considered “more efficient” than larger k-values. Thus, choosing 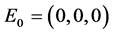
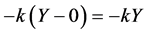
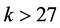
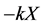

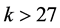
However, the method illustrated is trial-by-error, which makes it particularly well-suited for computer arithmetic. For example, choosing 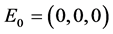
in the Z-equation is impossible. In this case, the characteristic polynomial of the Jacobian evaluated at 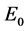
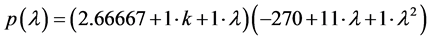
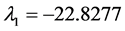
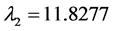
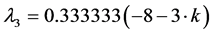
4. The Rössler Attractor
The three-dimensional version of the Rössler attractor is
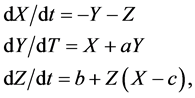
where a, b, and c are positive constants.
System (4) has been extensively studied and, consequently, its equilibria and the behavior of system (4) are well understood. Figure 5 illustrates chaos in the Rössler attractor using the parameter values 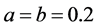
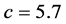
For these parameter values, system (4) has the following equilibrium points
Figure 3. Stabilizing 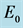
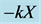

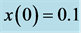
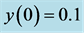
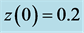
Figure 4. Stabilizing 
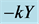


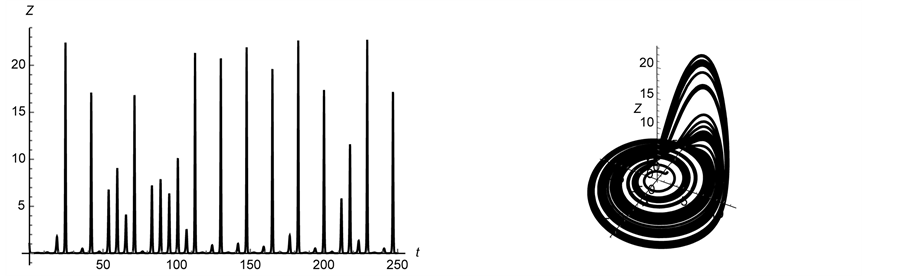
Figure 5. Chaos in the Rössler attractor using “typical” parameter values and initial conditions, 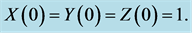
Following the same approach as in the previous example, we start by searching for a controller of the form 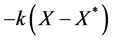
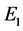
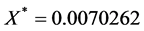
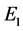
To guarantee that the eigenvalues of 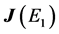
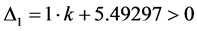
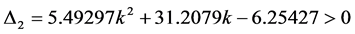
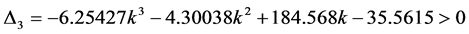
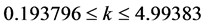
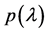
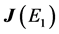

For this example, choosing to stabilize 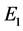
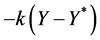
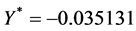
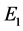

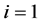
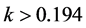
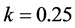
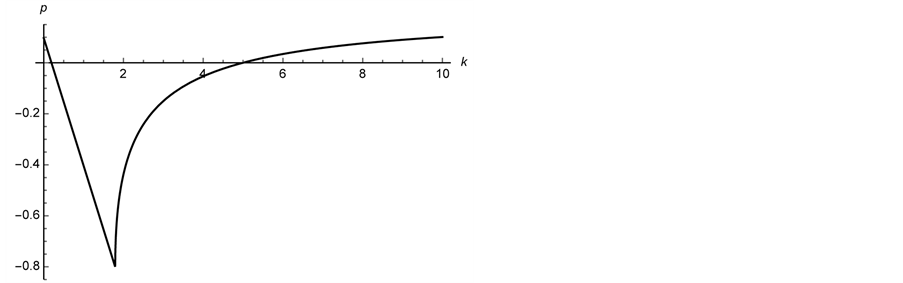
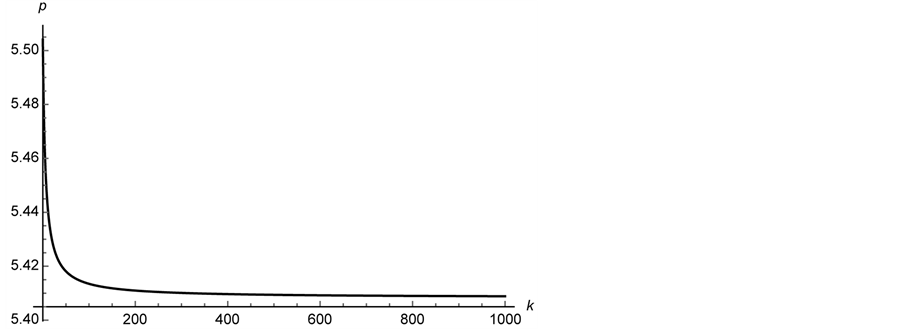
Figure 6. A plot of the maximum value of the real part of the zeros of 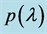
Figure 7. Stabilizing 
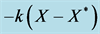
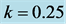
Figure 8. Stabilizing 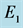

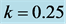
It is not possible to stabilize the system using a control of the form 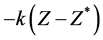
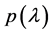
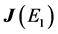

5. High-Himensional Rössler Attractors
Using the same notation as Musielak and Musielak, [1] , the four dimensional Röseller system
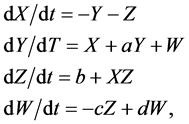
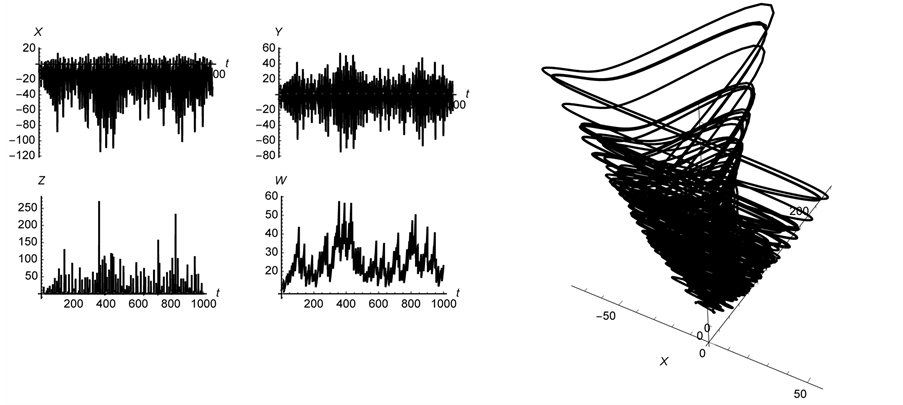
where a, b, c, and d are positive constants can exhibit more complex behavior than system (4). System (5) is interesting because depending upon the parameter values and initial conditions chosen, the system can exhibit hyperchaos, which is illustrated in Figure 10 using the parameter values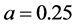

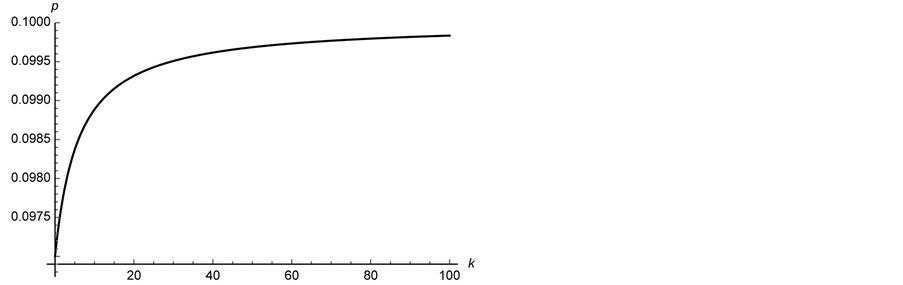
Figure 9. A plot of the maximum value of the real part of the zeros of 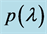
Figure 10. The 4-dimensional Rössler system exhibiting hyperchaos. The initial conditions are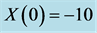
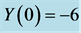
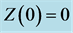

Figure 11. The behavior of the 4-dimensional system is highly dependent on the initial conditions. The initial conditions used are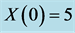


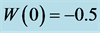
For these parameter values, system (5) has the following equilibrium points
The Jacobian of system (5) evaluated at each equilibrium point has the following eigenvalues
so both 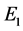


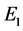
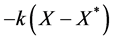
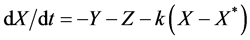
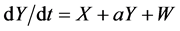
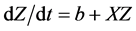


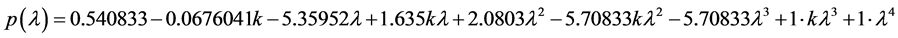
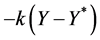

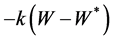
Next, we attempt using multiple controls. First, we try to find a control of the form 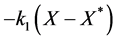
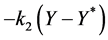
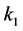

Next, we try to find a control of the form 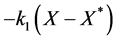
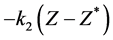
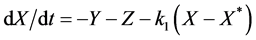
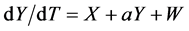
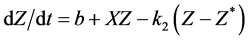
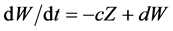
Figure 12. A plot of the maximum value of the real part of the zeros of 
The characteristic polynomial of 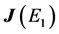
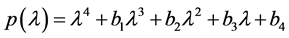
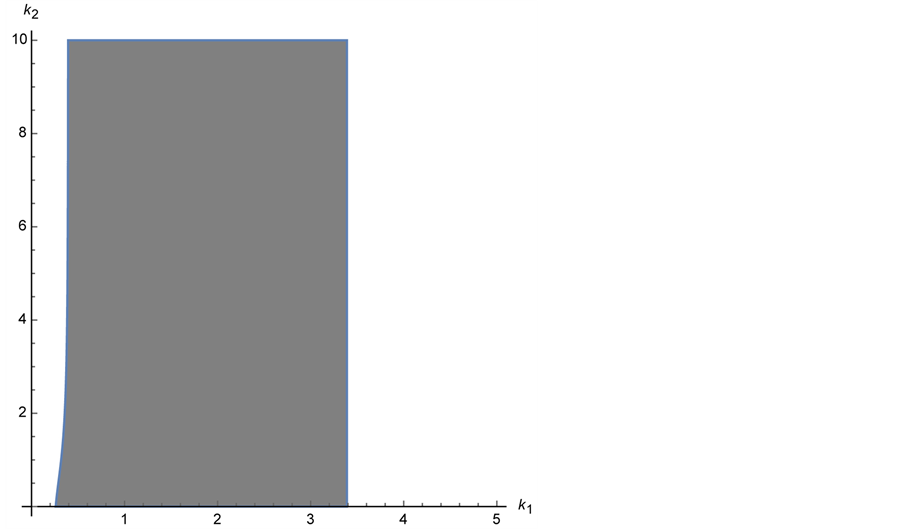
We plot the region where the maximum value of the real part of any zero of 
(1) Given 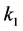
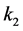
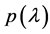
(2) Compute the real part of each zero and find the maximum real part of all zeros.
(3) Plot the region where the maximum value of the real part of any zero of 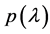
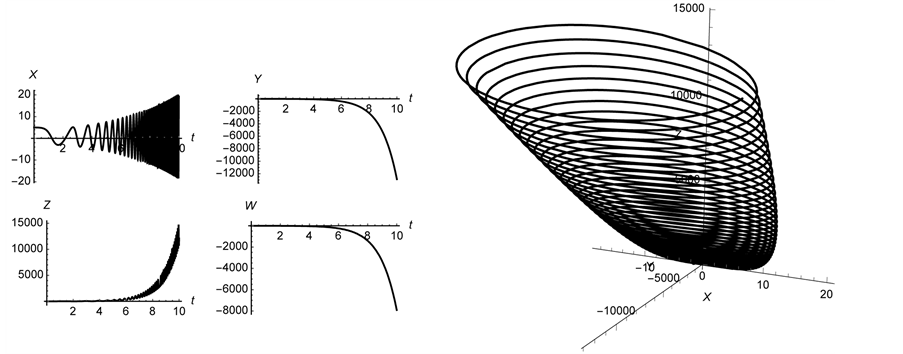
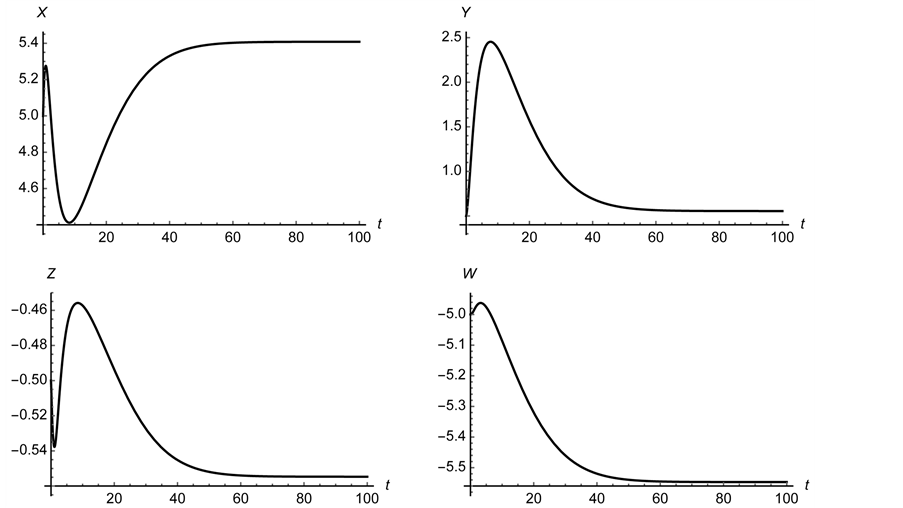
We find that we can control the system and stabilize 
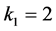

The Jacobian of this system evaluated at each equilibrium point has the following eigenvalues
which shows us that 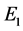
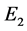
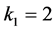

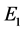
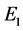
Figure 13. In the shaded region, the real part of all the zeros of 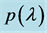
Figure 14. The system is stabilized using the initial conditions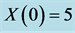
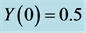
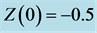
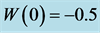
6. Conclusion
In this paper, we have illustrated an elementary algorithm to find a linear control that can stabilize a high- dimensional continuous dynamical system that exhibits chaotic behavior. We demonstrate how the technique is implemented and that it is well-suited for computer arithmetic using the Lorenz equations and Rössler attractor
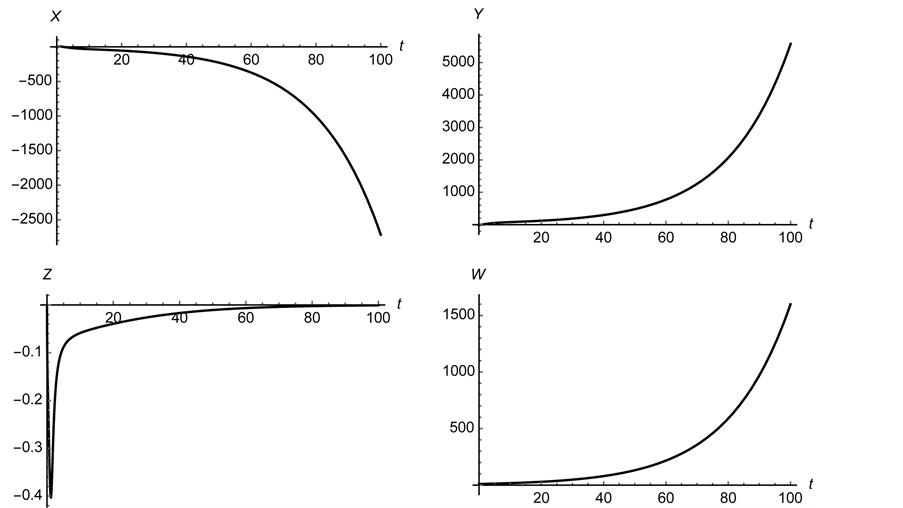
Figure 15. The control does not globally stabilize the system. The initial conditions are the same as those used in Figure 10.
as examples because they are very different models, but well studied and familiar to a wide audience. The simulations illustrated here show that the technique works on a wide range of dynamical systems, which we hope to further illustrate in later studies. Our simulations also indicate that it does not matter whether one uses the Routh-Hurwitz theorem or the characteristic polynomial to determined conditions on when all the eigenvalues of a matrix have negative real part. In future studies, we will focus on the physical interpretations of the controls that are introduced here as well as discuss conditions under which the control algorithm works or does not.
Computational Notes
The Mathematica, [7] , notebooks that the authors used to carry out the calculations as well as generate the figures here are available from the authors by sending a request to Jim Braselton at jbraselton@georgiasouthern.edu.
Cite this paper
JamesBraselton,YanWu, (2016) Applying Linear Controls to Chaotic Continuous Dynamical Systems. Open Journal of Applied Sciences,06,141-152. doi: 10.4236/ojapps.2016.63015
References
- 1. Musielak, Z.E. and Musielak, D.E. (2009) High-Dimensional Chaos in Dissipative and Driven Dynamical Systems. International Journal of Bifurcation and Chaos, 19, 2823-2869.
- 2. Chun, F.Y., Wang, H., Hu, Y. and Yin, J.W. (2012) Antisynchronization of a Novel Hyperchaotic System with Parameter Mismatch and External Disturbances. Pramana-Journal of Physics, 79, 81-93.
- 3. Li, Y. and Li, B. (2009) Chaos Control and Projective Synchronization of a Chaotic Chen-Lee System. Chinese Journal of Physics, 47, 261-279.
- 4. Tan, X., Zhang, J. and Yang, Y. (2003) Synchronizing Chaotic Systems Using Backstepping Design. Chaos, Solitons, Fractals, 16, 37-45.
- 5. Vieira, D. and Lichtenberg, A.J. (1966) Controlling Chaos Using Nonlinear Feedback with Delay. Physical Review E, 54, 1200-1207.
- 6. Wang, X.Y. and Wu, X.J. (2006) Tracking Control and Synchronization of Four-Dimensional Hyperchaotic Rössler System. Chaos, 16, 03312. http://dx.doi.org/10.1063/1.2213677
- 7. W. R. Inc. Mathematica, Version 10.0, 2014.