Received 26 August 2015; accepted 11 October 2015; published 14 October 2015

ABSTRACT

This paper tries to make a comparison and connection between Fokker-Planck or forward Kolmogorov equation and psychological future time which is based on quantum mechanics. It will be showed that in quantum finance forward interest rate model can be further improved by noting that the predicted correlation structure for field theory models depends only on variable where t is present time and x is future time. On the other side, forward Kolmogorov equation is a parabolic partial differential equation, requiring international conditions at time t and to be solved for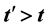. The aforementioned equation is to be used if there are some special states now and it is necessary to know what can happen later. It will be tried to establish the connection between these two equations. It is proved that the psychological future time if applied and implemented in Fokker-Planck equation is unstable and is changeable so it is not easily predictable. Some kinds of nonlinear functions can be applied in order to establish the notion of psychological future time, however it is unstable and it should be continuously changed.

Keywords:

Psychological Future Time, Fokker-Planck Equation, Kolmogorov Forward Equation, Lagrangian, Nonlinear Future Time

1. Introduction

In order to establish the connection between these two equations, firstly, Fokker-Planck equation will be derived. The approach that will be used is fairly simple and effective. Psychological future time will be analysed and afterwards the connection between these two equations will be established. It is well known that one can predict very little about long-term behavior of the market, the best thing that can be achieved is to have some credible models for a one-two year time. If Fokker-Planck equation describes the time evolution of the probability density function of the velocity of a particle under the influence of drag and random forces, it can be used to demonstrate the probability density function of psychological behavior and that is the key moment. By deriving Fokker-Planck equation, we will be using path integral approach and we will try to connect it to psychological future time. At the end of this section, we will introduce the Fokker-Planck equation.

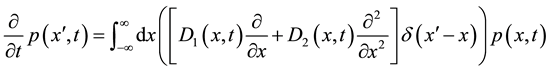(1)

where is the probability density of the random variable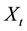;, 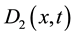are diffusion coeffi-

cients and 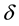is the function. The Fokker-Planck equation is the partial differential function that introduces the time evolution of the probability density function. The probability density function mimics Brownian motion as it is the density function of a particle under random forces.

2. Theoretical Background

Psychological future time

As we know that the predicted correlation structure for field theory models depends only on variable 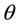which is a measure how far in the future is the future time [1] . We will start the derivation by replacing future time by some nonlinear function that is to be determined from the market. This variable measures the psychological future time in minds of investors and it is proportional to calendar future time given by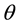. The psychological future time should be specified in conjunction with Lagrangian. General features of the function are the following [1] :

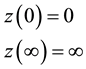(2)

The independent variables are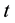,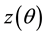. The forward rates from the market are always given for where denotes present time and so both future calendar time as well as psychological future time are necessary to connect with the market. The defining function for psychological future time is given by [1] :

(3)

where depends only on calendar time. It is obvious that both future times, namely and psychological time occur in the theory [2] .

The Lagrangian for psychological future time is written as [2] :

(4)

where is a two dimensional quantum field.

The propagator for is and the martingale condition for psychological future time is given by [1] :

(5)

Hence, we will analyse and make the difference between psychological future time and maturity dependence to the rigidity. For rigidity function, the Lagrangian of the rigidity function is the following [1] :

(6)

With a change of variable from to the action is given by:

(7)

Here the equation demonstrates that the Lagrangian for some non-linear function has an additional Jacobian factor.

The introduction of nonlinear future time is a new way of thinking of the interest rate models. In the framework of field theory, can be used to gain insight into subjective future time for market players.

Now we will derive the Fokker-Planck equation using path integral. The approach is taken from Janssen H.K. (1976) [3] .

If we write the Fokker-Planck equation in the form:

(8)

If we integrate over a time interval,where we get [4] :

(9)

By inserting the Fourier integral [5]

(10)

for the function, we obtain [4] :

(11)

The given equation will be useful for our further analysis. In the end we will show the Lagrangian of the function.

The variables and are called response variables.

3. Theoretical Findings

If we take the following form of Fokker-Planck Equation (10), eliminate i as it is characteristic to Schrodinger equation and in finance it doesn’t play a role and if we change the diffusion coefficients with the following for-

mulas, we get the following equation:

(12)

and we now obtain Lagrangian in the following form

(13)

The Lagrangian for the psychological future time is

(14)

It is obvious that Fokker-Planck equation is capable to take a function and translate it to future time which is given by. As the time is being translated, we can try the following formulation:

Now the psychological future time is translated into the future and the equation shows how will the function be affected. If we compare both Lagrangian for the Fokker-Planck equation and psychological future time, we get the following:

(15)

In order to have the equality valid, the following elements must be equal:

(16)

This can only be equal if we introduce the expectation of psychological future time:

(17)

Diffusion coefficients must be equal to the following form: and

which can be possible under the conditions that the diffusion on quantum field is performed along the z axis.

The coefficient must be equal to which is a quantum field. In order the Fokker-Planck equation to

be used to project psychological future time, diffusion coefficient must be equal to the equations given above. As this is not in most of the cases possible as the notion of quantum field is weakly related to diffusion coefficient, it means that Fokker-Planck equation will take psychological future time from the present to the future state but it will be changed because of diffusion coefficients that tend to change the perception of psychological future time. This proves that psychological future time is unstable and cannot be easily predicted. Credible models can be made for a short time. Further attention should be directed in the direction of trying to project how will the psychological future time will be changed.

4. Conclusion

This paper demonstrated that psychological future time cannot be easily predicted by using nonlinear function and Fokker-Planck equation. Psychological future time is different from the objective notion of time and is continuously changeable. Fokker-Planck equation takes the psychological future time from present to future but in a different shape because of diffusion coefficients. Although the paper tried to make two Lagrangians pertaining in that sense to Fokker-Planck equation and Lagrangian of psychological future time equal, it was proved that the aforementioned approach is not possible. This paper proved that future psychological time is different from the ordinary notion of time and is continuously changing. Next step is to capture the rate of change which will be tried to be addressed in the future papers.

Acknowledgements

I want to thank my family for immense support, especially my father who is a big support and my pride.

Cite this paper

OgnjenVukovic, (2015) On the Application of Fokker-Planck Equation to Psychological Future Time. Open Journal of Applied Sciences,05,571-575. doi: 10.4236/ojapps.2015.510055

References