Open Journal of Applied Sciences
Vol.05 No.09(2015), Article ID:59555,14 pages
10.4236/ojapps.2015.59051
Fuzzy Logic Strategy for Solving an Optimal Control Problem of Therapeutic Hepatitis C Virus Dynamics
Jean Marie Ntaganda1, Mahamat Saleh Daoussa Haggar2*, Benjamin Mampassi3
1College of Science and Technology, School of Sciences, Department of Mathematics, University of Rwanda, Butare, Rwanda
2Department of Mathematics, Faculty of Exact and Applied Sciences, N’Djamena University, N’Djamena, Chad
3Department of Mathematics, Faculty of Sciences and Technology, Dakar University, Dakar, Senegal
Email: jmnta@yahoo.fr, j.m.ntaganda@ur.ac.rw, *daoussa_haggar@yahoo.fr, mampassi@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 July 2015; accepted 11 September 2015; published 14 September 2015
ABSTRACT
This paper aims at the development of an approach integrating the fuzzy logic strategy for a therapeutic hepatitis C virus dynamics optimal control problem. To test the efficiency of this strategy, the authors propose a numerical comparison with the direct method by taking the values of determinant parameters of this disease for people administrating the drugs. The results are in good agreement with experimental data.
Keywords:
Fuzzy Logic, Optimal Control, Membership Function, Membership Degree, Hepatitis C Virus, Uninfected Hepatocytes, Infected Hepatocytes, Numerical Simulation

1. Introduction
In the 1970s and 1980s, serological tests developed hepatitis A virus (HAV) and B viruses (HBV) which indicated that most transfusion-associated hepatitis was not caused by either HAV or HBV, which was therefore named non-A, non-B hepatitis (NANBH). After detection of the first NANBH-specific clone, the entire viral genome of the now termed hepatitis C virus (HCV) was sequenced. Hepatitis C is a liver infection caused by the Hepatitis C virus (HCV). HCV is a small positive-strand ribonucleic acid (RNA) virus in the Flaviviridae family where it forms its own genus hepacivirus [1] . At least six viral HCV genotypes are identified, numbered 1 to 6 [2] ; most genotypes have been divided into multiple subtypes (e.g., genotype 1 subtypes 1a and 1b). The chronic hepatitis C (CHC) causes cirrhosis and hepatocellular carcinoma and, without effective treatment interventions, significant increases in CHC associated morbidity, mortality, and health care costs are predicted [3] .
HCV can be transmitted by transfusion of blood and blood products, transplantation of solid organs from infected donors, injection drug abuse, unsafe therapeutic injections, and occupational exposure to blood (primarily contaminated needles) [4] . Transfusion-associated HCV infection was an important source of infection before HCV testing of blood donors was introduced in the early 1990s. Since then, transfusion-associated HCV infection has been virtually eliminated in those countries where routine HCV-testing has been implemented (Safe Injection Global Network (SIGN, 2001)). HCV is less efficiently transmitted by occupational, perinatal and high- risk sexual exposures compared to those involving large or repeated percutaneous exposures to blood [4] .
To date, an active or passive vaccination against HCV is not yet available. The main factor that hampers the development of an efficient vaccine is the considerable genetic heterogeneity of this positively-stranded RNA virus. However, better understanding of the natural immunity to HCV and the proof of vaccine efficacy in the chimpanzee challenge model allow some optimism about the development of an at least partly effective vaccine against this heterogeneous pathogen [5] .
The ultimate goal of CHC treatment is to reduce the occurrence of end-stage liver disease and its complications including decompensated cirrhosis, liver transplantation, and hepatocellular carcinoma (HCC). However, because progression of liver disease occurs over a long period of time, clinicians use sustained virologic response (SVR), defined as lack of detection of HCV RNA in blood several months after completing a course of treatment, to determine treatment success. SVR is considered a virologic cure [6] . Total duration of treatment and choice of regimen may depend on HCV genotype or subtype and host genotype. For many years, the standard of care for treatment of CHC had been a combination of pegylated interferon alpha-2 (peg-IFN) and ribavirin (RBV) administered for 24 (genotypes 2 and 3) or 48 weeks (genotype 1 and others). There are three types of interferon: alfa (IFN-a), beta (IFN-b) and gamma (IFN-g). Interferon alfa is used to treat viral hepatitis and some types of cancer. The type 1 IFNs [interferon alpha and beta (IFN-a/b)] comprise a family of distinct proteins [7] [Takaoka] that are produced by a wide variety of cells, including fibroblasts, epithelial cells, and hepatocytes [8] , although plasmacytoid dendritic cells (DCs) are probably the major source in most viral infections. In contrast, type II IFN [interferon gamma (IFN-g)] is a single gene cytokine unrelated in structure to IFN-a/b that is produced largely by macrophages, natural killer (NK) cells, and T lymphocytes. Both types of IFNs interact with cells via distinct cellular receptors. The details of the signaling mechanisms by which IFN-a/b and IFN-g induce the transcription of interferon-stimulated genes (ISGs) and depress the transcription of others are still being defined [9] . However, it is increasingly clear that the complex transcriptional programs induced differ significantly depending on the IFN type, the cellular target, and the nature of the infection/host challenge. IFN-a/b produced by DCs activates NK cells, enhancing their cytotoxic potential and stimulating their production of IFN-g, whereas other cytokines such as interleukin-15 (IL-15) induced by IFN-a/b stimulate the proliferation and accumulation of NK cells [10] [11] . IFN-a/b produced by DCs also modulates the activation of CD8+ T cells, which produce additional IFN-g and represent the central players in the pathogen-specific adaptive immune response [12] . With peg-IFN- and RBV-based therapy, viral relapse usually occurs within the first few weeks following treatment cessation and measurement of SVR at an earlier time point could yield greater trial efficiency [13] . Interferon is a protein made by the immune system, named because it interferes with viral reproduction. In addition, interferon signals the immune system to recognize and respond to microorganisms, including viral and bacterial infections. Ribavirin, also known as Copegus, Rebetol, Virazole, or a component of Rebetron, is a type of antiviral medicine called a nucleoside analogue. This medicine blocks the ability of the hepatitis C virus (HCV) to make more copies of itself. Ribavirin is not active against HIV. Ribavirin is used in combination with interferon alfa-2a or -2b or peginterferon alfa-2a or -2b to treat HIV infected patients who are also infected with HCV. Ribavirin capsules are indicated in combination with INTRON A (interferon alfa-2b, recombinant) injection for the treatment of chronic hepatitis C in patients 18 years of age and older with compensated liver disease previously untreated with alpha interferon or in patients 18 years of age and older who have relapsed following alpha interferon therapy. Ribavirin is a broad spectrum antiviral agent that is used with pegylated IFN (Peg-IFN) for HCV treatment. Ribavirin does not significantly reduce HCV viral load when used alone but increases rates of sustained virologic response (SVR) when combined with Peg-IFN. Infected cells release interferon to trigger the immune response. In patients infected with genotype 1 or 4, HCV eradication rates range between 45% and 52%. In contrast, in patients infected with HCV genotype 2 or 3, antiviral therapy results in HCV eradication in 75% - 90% of cases. Furthermore, HCV genotype 1 infected patients require higher doses of ribavirin administered for a longer duration of time versus HCV genotypes 2 and 3 patients who respond effectively to Peg-IFN with lower doses of ribavirin and shorter duration of therapy. Higher serum concentrations of ribavirin are associated with higher response rates but also higher rates of hemolytic anemia which is a dose limiting side effect. Currently, several novel antiviral agents are being evaluated in individual studies, which are NS3-4A protease inhibitors, RNA-dependent RNA polymerase inhibitors, and different immune therapies [14] .
Mathematical modelling and quantitative analysis of hepatitis C infections has been explored extensively over the last decade. Most of the modelling has been restricted to the short term dynamics of the model. One of the earliest models was proposed by Neumann et al. [15] , who examine the dynamics of HCV in presence of Interferon-a (IFN-a) treatment. They find that the primary role of IFN is in blocking the production of virions from the infected hepatocytes. However, IFN has little impact when it comes to controlling the infection of the hepatocytes. Dixit et al. [16] improved upon [15] by including the effects of ribavirin, which in turn results in a fraction of the virions being rendered noninfectious. Their model is able to explain clinically observed biphasic decline patterns amongst patient population. Their study also shows that while IFN plays a pivotal role in the first phase decline of viral load, ribavirin has very little impact. However, in case of low IFN efficacy, ribavirin makes a significant contribution to the second phase of decline. The model could not successfully explain the triphasic decline patterns, as well as some cases of non-responders. Dahari et al. [17] in a subsequent and improved model, take into account the homeostatic mechanisms for the liver by incorporating a growth function. This model successfully explains the triphasic decline, as well as therapeutic failures.
Control theory has found wide ranging applications in biological and ecological problems [18] . In the case of HCV, Chakrabarty and Joshi [19] consider a model (motivated by [15] - [17] for HCV dynamics under combination therapy of interferon and ribavirin. An objective functional is formulated to minimize the viral load, as well as the drug side-effects and the optimal system is solved numerically to determine optimal efficacies of the drugs. Chakrabarty [20] extended the results in [19] by considering a clinically validated functional form for the interferon efficacy and hence determined the optimal efficacy of ribavirin. Martin et al. [21] in a recent paper examine a three compartment model for HCV, involving the susceptible, chronically infected and treated injecting drug users (IDUs). They determine an optimal treatment programme over a 10 year period taking into account several biomedical and economic objectives. The objective of this paper is to find a new mathematical model of therapetic hepatitis C virus dynamics with treatment of two drugs, which is combination treatment with IFN and ribavirin.
In this paper we are interested in the role of drugs and how they play a crucial role in controlling HCV diseases through a bicompartmental model such that the controls are those drugs. Therefore, the formulation of optimal control problem is done. There are the numerous methods that allow solving this kind of problem. We prefer to make a comparative study of direct method with another approach based on the fuzzy logic strategy.
This paper is organized as follows. Section 2 presents the model equations and optimal control problem. A short description of strategy approach by fuzzy logic for solving optimal control problems is discussed in this section. Section 3 is interested in presentation of the direct approach and the approach integrating the fuzzy logic for solving an optimal control problem of hepatitis C. The numerical simulation is presented in Section 4. Finally, we present concluding remarks in Section 5.
2. Methods
2.1. Setting of the Problem
In terms of constraints of our problem, we consider a two compartmental mathematical model proposed in [22] .
This mathematical model is formulated from a diagram given in Figure 1.
The model equations are as follows:
 (1)
(1)
 (2)
(2)
where
 (3)
(3)
Figure 1. A schematic diagram of two compartments for modeling human hepatitis C virus dynamics. PBr is blood pressure. IFN is interferon and Rib is ribavirin. H and I represent uninfected hepatocytes and infected hepatocytes respectively. The function f and g r represent the mechanism of control of hepatitis C virus. This mechanism is not direct and can be represented by outflow functions between uninfected hepatocytes and infected hepatocytes compartments that depend on interferon (IFN) and ribavirin (Rib) which flow in lever through circulatory system by blood pressure.These f and g must be identified.
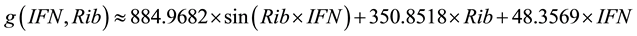 (4)
(4)
If 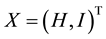 is a state vector, then the healthy improvement conditions for an uninfected human should look for reaching uninfected steady state
is a state vector, then the healthy improvement conditions for an uninfected human should look for reaching uninfected steady state 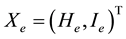 where
where 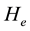 is the constant that must be found out. Since
is the constant that must be found out. Since , next the cost function (objective function) was formulated in the following way.
, next the cost function (objective function) was formulated in the following way.
Find  and
and  solution of
solution of
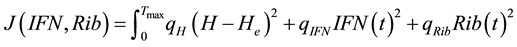 (5)
(5)
subject to the system (1) - (2).
The positive scalar coefficients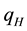 ,
,  and
and 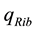 determine how much weight is attached to each cost component term in the integrand whereas
determine how much weight is attached to each cost component term in the integrand whereas 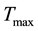 denotes the maximum time that the physical activity can take.
denotes the maximum time that the physical activity can take.
2.2. Description of Fuzzy Logic Strategy Approach
To describe fuzzy logic strategy approach, we consider a linear quadratic problem which can be formulated as follows. For two positive defined matrices 




subject to

The methods with a fast convergence can be used to solve the problem (6) - (7). One of these methods is dynamic programming method which is quadratically convergent. Furthermore, a state of control feedback is an optimal solution for this mathematical method [23] . Although this method is used to solve the linear quadratic problem, the solution in some cases is not optimal because this method this method depends on the choice of the initial trajectory. Therefore, another method can be taken, we prefer for this reason, the method which integrates the fuzzy logic in order to determine quickly the optimal solution [24] . Fuzzy logic strategy approach is based on the linearization of state system. This approach had been developed by Takagi-Sugeno [25] [26] . It is from the mathematical model introduced in 1985 by Takagi-Sugeno that is used to get some fuzzy linearization regions in the state space [27] . These linearization regions are fuzzy regions where the operating points are taken. From the idea of Takagi-Sugeno, the nonlinear system decomposition in a structure multi models which are independent linear models [28] . The mechanism of linearization using fazzy logic strategy for a nonlinear system (NL) can be described as follows.
If 


1) The approximation of order zero which satisfies:

2) Taylor expansion series of first order verifying

To minimize the error between the non linear function and the fuzzy approximation, we introduce the factor of the consequence for fuzzy Takagi-Sugeno system that allows the improvement of approximation (8) or (9). Taking 

The following expression is obtained from the replacement of nonlinear term 



where 




The outcome of approximation of nonlinear term 

where

is the feedback gain matrix and 

From (12) S controls are determined and the defuzzyfication method [26] leads to only one system and only one control 


where

and where 

3. Numerical Approaches for Solving the Optimal Control Problem (5) Subject to (1) - (2)
3.1. Using Fuzzy Logic Strategy
Since explicit Euler scheme is stable, it is used to approximate the optimal control problem (5) subject to (1) - (2). This method is an advantage to approach some ordinary differential equations. The following system is obtained from Taylor expansion around 


where
Using the variable change

the system (18) becomes

On the uniform grid and from the system (20) yields the following approximated system

where 

To determine the Takagi-Sugeno fuzzy system and using the form given by expression (8) or (9), now we focus on linearization of two nonlinear factors of the system (21) that is
This mechanism is done by taking the points 





Let us note 


where



Now we are interested in approximating the objective function of the problem (5). Hence, using rectangular method the following expression yields

where matrices 

such that the optimal control problem () subject to () - () can be formulated as follows.
Find 

subject to

The problem (28) - (29) is a linear quadratic (LQ) such that for each

where 
3.2. Using Direct Approach
Firstly, the direct method focuses on approximation of the system (1) - (2) on uniform grid

where we define a linear B-splines basis functions of the form

such that we have the relation

where 

This approximation is done by introducing the vector space 

1)
2)
Assuming 

satisfying

we are able to verify easily that


Furthermore, the approximation of the system (1)-(2) can be formulated as follows.
Find 



such that


Secondly, the direct method deals with the discretization of the optimal problem (5) which becomes

where
with 




Taking 


Using rectangular method such that the discretization is done on a regular grid 

Therefore, the discrete formulation of optimal problem (5) subject to (1) - (2) is written as follows.

where 











Taking the approximated objective function (45) and (37) - (38) satisfying (40) and (41) into account, the optimal control problem (5) subject to (1) - (2) is a minimization problem with constraint such that discreet formulation of such problem can be formulated as follows.
Find 

subject to

where 










4. Numerical Simulation
Using the mechanism of linearization of the nonlinear terms of the system (21), we apply the fuzzy strategy and we consider the case of health person where we take 

We consider a universe of discourse 








According the relation (19) and equilibrium values, we have 


Let us set 

Table 1. Variables and their operating points.

Figure 2. Triangular membership functions associated to operating points −800, −150, and 500 (respectively 0, 150 and 300) for the linguistic variable UH (a) (respectively IH (b)) according to the variable change (19). 500 and 250 are the values of entries obtained thanks to the formula (19).
It easy to note that the problem (28) - (29) is a linear quadratic (LQ). Since there are three linear state systems, the solution leads to three feedback controls of the form

where 
The implementation can be made in several platforms. Here we use MATLAB package. Taking 

The defuzzification transformation allows to obtain one system. Consequently, for the system (29) this technique gives the following system

where 




In the same way, from the matrixes 


The first (respectively second) line of matrixes 






i) We consider the degree of membership of the entry uninfected hepatocytes (respectively infected hepatocytes). According to variable change (19), this value is 400 cells/dl (see Figure 2(a)) (respectively 120 cells/dl (see Figure 2(b)))). After calculations, we get

[resp. 


ii) The nonlinear factor
is used only in the first (respectively second) equation of the system (22).
Considering these hypothesis, we have the following matrixes.
The solutions of the optimal control problem (28) - (29) and (47) - (48) can be determined in several platform. The implementation of these solutions is made using MATLAB packages.
To solve the problem (28) - (29) by fuzzy logic strategy only one program is enough. Using direct approach, the solutions of the problem (47) - (48) are given by a succession of programs based on MATLAB function used in optimization that is fmincon. This function is a MATLAB program which allows solving minimization problem with constraints.
In this section, we note by AHLF, ADIR to designate respectively the hybrid approach integrating fuzzy logic strategy and direct approach. Consequently, Table 2 gives us the results found after the execution of main
Table 2. Minimal values of the objective function (Jopt) and the execution time (T) of main program for the resolution of the optimal control problem (28) - (29) by AHLF and (47) - (48) by ADIR.
MATLAB program for AHLF, ADIR respectively. The results are obtained using a Processor Intel (R) core (TM) 2 Duo CPU, 2.20 GHZ.
Table 2 shows that the time execution of the main program to solve the problem (28) - (29) by AHLF is very small compared to one obtained by solving the problem (47) - (48) using ADIR . This argument justifies the efficiency of the fuzzy logic strategy.
Considering a patient who is administrating the drugs during 12 months, the variations of the optimal parameters is obtained using the hybrid approach integrating fuzzy logic strategy (AHLF) and the direct approach (ADIR). Numerical results of fuzzy logic strategy are obtained from the resolution of the problem (28) - (29) such that the controls are calculated using the relation (30). Solving the problem (47) - (48), we have the numerical results of direct approach. Figure 3 and Figure 4 illustrate comparison of the results of those two different methods.
Figure 3 illustrates both interferon (IFN) that is used to prevent the virus from infecting the cell (Figure 3(a)) and ribavirin (Rib) that allows the prevention of the infected cells from producing the new viruses (Figure 3(b)). Figure 4 presents the response of these chemotherapy to variation of the concentration of uninfected hepatocytes (Figure 4(a)), infected hepatocytes (Figure 4(b)). For a patient who is administrating regularly the drugs, we see that interferon (IFN) and ribavirin (Rib) decrease and after 4months they reach the lower value 0 (maximal use of therapy) before having its oscillation around this value (Figure 3(a) and Figure 3(b)). The solutions from AHLF and ADIR show that after 2.5 minutes of the starting time the optimal uninfected hepatocytes (Figure 4(a)) increases to reach the wanted equilibrium value and infected hepatocytes (Figure 4(b)) decreases gradually to reach the value around the wanted value in 6 months before its oscillation around this value.
It is known that the main aim of treatment for chronic hepatitis C is to suppress HCV replication before there is irreversible liver damage. Furthermore, the role of drugs on chronic hepatitis C virus is to reduce the risk of liver disease and prevent the patient from passing the infection to others. The variation of controls given in Figure 3 which shows the decrease from 1 (when and treatment is absent) of both interferon (IFN) and ribavirin (Rib) to be closer to the lower value 0 (maximal use of therapy). Figure 4(a) (respectively 4(b)) shows a increase (respectively decrease) of uninfected hepatocytes (respectively infected hepatocytes) to its higher (respectively lower) value during the six first months of the beginning of the process before oscillating around the wanted equilibrium value. This behaviour is due to action of therapeutic drugs. The results obtained in this work are rather satisfactory. In particular, the reaction of the disease to drugs can be modeled and they reduce the risk of it. Therefore the drugs play a crucial role such that any patient becomes healthy. Comparing the results using AHLF and ADIR, it is important to see in Figure 3 and Figure 4 that they are very closed.
5. Concluding Remarks
This work deals with an optimal control problem related to uninfected hepatocytes and infected hepatocytes of hepatitis C virus. To handle that problem, two numerical approaches have been compared to determine the optimal trajectories of these determinant parameters which respond to two controls (interferon and ribavirin) of this disease hepatitis C virus for a patient who is administrating drugs during 12 months. The results show that two used methods are satisfactory and closed. The findings also show that, in terms of time, the hybrid approach integrating the fuzzy logic strategy has an advantage on the direct approach in terms of time. Consequently, it constitutes an important approach for the resolution of the optimal control problem. In particular, it gives the optimal trajectories of uninfected hepatocytes and infected hepatocytes in the same way that it ensures their

Figure 3. Variation of drugs (controls) interferon, IFN (a) and ribavirin, Rib (b). The curves in dotted line represent the parameter for the the direct approach. The curve dashed line show the parameter for the approach integrating the fuzzy logic approach.

Figure 4. Variation of the concentration of uninfected hepatocytes (a), infected hepatocytes (b) for a patient. The curves in dotted line represent the parameter for the direct approach. The curve dashed line show the parameter for the approach integrating the fuzzy logic strategy.
performance.
Cite this paper
Jean MarieNtaganda,Mahamat Saleh DaoussaHaggar,BenjaminMampassi, (2015) Fuzzy Logic Strategy for Solving an Optimal Control Problem of Therapeutic Hepatitis C Virus Dynamics. Open Journal of Applied Sciences,05,527-541. doi: 10.4236/ojapps.2015.59051
References
- 1. Choo, Q.L., Kuo, G., Weiner, A.J., et al. (1989) Isolation of a cDNA Clone Derived from a Blood-Borne Non-A, Non-B Viral Hepatitis Genome. Science, 244, 359-362. http://dx.doi.org/10.1126/science.2523562
- 2. Simmonds, P., Bukh, J., Combet, C., et al. (2005) Consensus Proposals for a Unified System of Nomenclature of Hepatitis C Virus Genotypes. Hepatology, 42, 962-973. http://dx.doi.org/10.1002/hep.20819
- 3. Kim, W.R. (2002) The Burden of Hepatitis C in the United States. Hepatology, 36, S30-S34.
- 4. Alter, M.J. (2007) Epidemiology of Hepatitis C Virus Infection. World Journal of Gastroenterology, 13, 2436-2441. http://dx.doi.org/10.3748/wjg.v13.i17.2436
- 5. Houghton, M. and Abrignani, S. (2005) Prospects for a Vaccine against the Hepatitis C Virus. Nature, 436, 961-966. http://dx.doi.org/10.1038/nature04081
- 6. Shiratori, Y., Ito, Y., Yokosuka, O., Imazeki, F., Nakata, R., Tanaka, N., Arakawa, Y., Hashimoto, E., Hirota, K., Yoshida, H., Ohashi, Y. and Omata, M., Tokyo-Chiba Hepatitis Research Group (2005) Antiviral Therapy for Cirrhotic Hepatitis C: Association with Reduced Hepatocellular Carcinoma Development and Improved Survival. Annals of Internal Medicine, 142, 105-114.
- 7. Takaoka, A. and Yanai, H. (2006) Interferon Signalling Network in Innate Defence. Cellular Microbiology, 8, 907-922. http://dx.doi.org/10.1111/j.1462-5822.2006.00716.x
- 8. Li, K., Foy, E., Ferreon, J.C., Nakamura, M., Ferreon, A.C., Ikeda, M., et al. (2005) Immune Evasion by Hepatitis C Virus NS3/4A Protease-Mediated Cleavage of the Toll-Like Receptor 3 Adaptor Protein TRIF. Proceedings of the National Academy of Sciences of the United States of America, 102, 2992-2997. http://dx.doi.org/10.1073/pnas.0408824102
- 9. Honda, K., Takaoka, A. and Taniguchi, T. (2006) Type I Interferon [Corrected] Gene Induction by the Interferon Regulatory Factor Family of Transcription Factors. Immunity, 25, 349-360. http://dx.doi.org/10.1016/j.immuni.2006.08.009
- 10. Lee, S.H., Miyagi, T. and Biron, C.A. (2007) Keeping NK Cells in Highly Regulated Antiviral Warfare. Trends in Immunology, 28, 252-259. http://dx.doi.org/10.1016/j.it.2007.04.001
- 11. Young, H.A. and Ortaldo, J. (2006) Cytokines as Critical Co-Stimulatory Molecules in Modulating the Immune Response of Natural Killer Cells. Cell Research, 16, 20-24. http://dx.doi.org/10.1038/sj.cr.7310004
- 12. Gil, M.P., Salomon, R., Louten, J. and Biron, C.A. (2006) Modulation of STAT1 Protein Levels: A Mechanism Shaping CD8 T-Cell Responses in Vivo. Blood, 107, 987-993. http://dx.doi.org/10.1182/blood-2005-07-2834
- 13. Chen, J., Florian, J., Carter, W., Fleischer, R.D., Hammerstrom, T.S., Jadhav, P.R., Zeng, W., Murray, J. and Birnkrant, D. (2013) Earlier Sustained Virologic Response End Points for Regulatory Approval and Dose Selection of Hepatitis C Therapies. Gastroenterology, 144, 1450-1455.
- 14. Manns, M.P., Foster, G.R., Rockstroh, J.K., Zeuzem, S., Zoulim, F. and Houghton, M. (2007) The Way forward in HCV Treatment—Finding the Right Path. Nature Reviews Drug Discovery, 6, 991-1000. http://dx.doi.org/10.1038/nrd2411
- 15. Neumann, A.U., Lam, N.P., Dahari, H., Gretch, D.R., Wiley, T.E., Layden, T.J. and Perelson, A.S. (1998) Hepatitis C Viral Dynamics in Vivo and the Antiviral Efficacy of Interferon-α Therapy. Science, 282, 103-107. http://dx.doi.org/10.1126/science.282.5386.103
- 16. Dixit, N.M., Layden-Almer, J.E., Layden, T.J. and Perelson, A.S. (2004) Modelling How Ribavirin Improves Interferon Response Rates in Hepatitis C Virus Infection. Nature, 432, 922-924. http://dx.doi.org/10.1038/nature03153
- 17. Dahari, H., Lo, A., Ribeiro, R.M. and Perelson, A.S. (2007) Modeling Hepatitis C Virus Dynamics: Liver Regeneration and Critical Drug Efficacy. Journal of Theoretical Biology, 247, 371-381. http://dx.doi.org/10.1016/j.jtbi.2007.03.006
- 18. Lenhart, S. and Workman, J.T. (2007) Optimal Control Applied to Biological Methods.
- 19. Chakrabarty, S.P. and Joshi, H.R. (2009) Optimally Controlled Treatment Strategy Using Interferon and Ribavirin for Hepatitis C. Journal of Biological Systems, 17, 97-110. http://dx.doi.org/10.1142/S0218339009002727
- 20. Chakrabarty, S.P. (2009) Optimal Efficacy of Ribavirin in the Treatment of Hepatitis C. Optimal Control Applications and Methods, 30, 594-600. http://dx.doi.org/10.1002/oca.894
- 21. Martin, N.K., Ashley, B., Pitcher, A.B., Vickerman, P., Vassal, A. and Hickman, M. (2011) Optimal Control of Hepatitis C Antiviral Treatment Programme Delivery for Prevention amongst a Population of Injecting Drug Users. PLoS ONE, 6, e22309. http://dx.doi.org/10.1371/journal.pone.0022309
- 22. Ntaganda, J.M. (2015) Modelling a Therapeutic Hepatitis C Virus Dynamics. International Journal of Scientific and Innovative Mathematical Research (IJSIMR), 3, 1-10. (Online)
- 23. Yakowitz, S.J. (1986) The Stagewise Kuhn-Tucker Condition and Differential Dynamic Programming. IEEE Transactions on Automatic Control, 31, 25-30. http://dx.doi.org/10.1109/tac.1986.1104123
- 24. Masmoudi, N.K. and Derbel, N. (2003) Optimal Control of Nonlinear Systems by Fuzzy Logic. ISCIII, Nabeul.
- 25. Sugeno, M. and Murakami, K. (1984) Fuzzy Parking Control of Model Car. 23rd IEEE Conference on Decision and Control, Las Vegas, 12-14 December 1984, 902-903. http://dx.doi.org/10.1109/CDC.1984.272144
- 26. Takagi, T. and Sugeno, M. (1985) Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Transactions on Systems, Man and Cybernetics, 15, 116-132. http://dx.doi.org/10.1109/TSMC.1985.6313399
- 27. Park, M.I., Kim, E., Ji, S. and Park, M. (1987) A New Approach to Fuzzy Modeling. IEEE Transactions on Fuzzy Systems, 5, 328-337.
- 28. Jacobson, D., Lele, D. and Speyer, J.L. (1971) New Necessary Conditions of Optimality for Control Problems with State-Variable Inequality Constraints. Journal of Mathematical Analysis and Applications, 35, 255-284. http://dx.doi.org/10.1016/0022-247X(71)90219-8
- 29. Kwakernaak, H. and Savan, R. (1972) Linear Optimal Control Systems. Wiley Inter-Science, New York.
- 30. Trélat, E. (2005) Contrôle optimal: Théeorie et applications. Vuibert, Collection Mathématiques Concrètes.
NOTES
*Corresponding author.


















