Open Journal of Applied Sciences
Vol.05 No.07(2015), Article ID:57828,11 pages
10.4236/ojapps.2015.57032
On a Non-Perturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 June 2015; accepted 6 July 2015; published 9 July 2015
ABSTRACT
In this paper we outline a non-perturbative quantum relativity theory. Subsequently an actual design of a nanotech energy reactor is based on spacetime vacuum fluctuation of the said quantum relativity theory. Using a compact heap of Fullerene nano particle moduli of a nano matrix device we propose that by maximizing the Casimir forces between these particles as a desirable effect, we can achieve a gradual rather than a sudden implosion pressure. We expect that this will result in a mini holographic universe from which energy can be extracted in a way to constitute a nano energy reactor and function effectively on a hybrid principle somewhere between a Casimir effect and a cold fusion process based on the fusion algebra of a highly structured golden ring quantum field theory. The present theory depends upon many concepts and results, in particular J. Schwinger’s source theory as well as the modern theory of quantum sets, nonlinear dynamics, chaos and chaotic fractals.
Keywords:
Quantum Relativity, Casimir Reactor, Dark Energy, Nano Spacetime Energy Reactor, Chaos and Fractals, Schwinger Source Theory, Fusion Algebra, Quantum Sets

1. Introduction
The author of the present paper feels strongly that he should make it abundantly clear from the outset that all the ideas presented here are influenced in no minor way by J. Schwinger’s source theory as well as his views on cold fusion and everything else follow from there (see Figures 1-3 and the comments therein). Here we start with E-infinity theory [1] -[4] which is based on transfinite set theory [4] [5] as well as substantial amounts of
Figure 1. Banach-Tarski sphere decomposition Cantorian spacetime of E-infinity theory that is considered here to model our actual spacetime may be envisaged advantageously as in this artist impression. This is basically a two dimensional projections in which each of the larger balls (circles) are a zero set
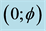 representing the quantum particle while the surface
representing the quantum particle while the surface
(circumference) represents the empty set
 which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set
which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set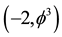 ,
,
i.e. the surface of the empty set quantum wave. Remarkably the average set of all zero and empty sets is an expectation value
equal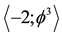 . In other words,
. In other words,
 is our quantum spacetime, which is the cobordism of the quantum wave, which in
is our quantum spacetime, which is the cobordism of the quantum wave, which in
turn is the cobordism of the quantum particle, floating and propagating with the help of its wave in our Cantorian E-infinity spacetime [1] [2] [10] [11] . It is likewise remarkable that
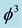 is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime. Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to firstly find the topological energy density by adding Kaluza-Klein D = 5 to
is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime. Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to firstly find the topological energy density by adding Kaluza-Klein D = 5 to
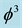 of the spacetime vacuum and find the fractal Kaluza-Klein dimension 5 +
of the spacetime vacuum and find the fractal Kaluza-Klein dimension 5 +
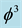 then multiply this with the average Cantorian interval speed of light c =
then multiply this with the average Cantorian interval speed of light c =
 squared. The result is
squared. The result is . Inserting in Newton’s kinetic energy one finds
. Inserting in Newton’s kinetic energy one finds
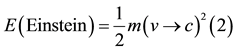
 exactly as should be. The preceding explanation amounts to a paradigm shift in physics where the totally empty vacuum of spacetime is taken as fundamental and everything else is derivable from it. To prove this point was a dream of Serbian American inventor N. Tesla who died in 1943 as well as Soviet physicist A. Zakharov. In fact in his later years Nobel Laureate J. Schwinger was a champion of cold fusion [12] which comes very near to our present concept of a Casimir-nano energy reactor [10] [11] . We also stress that we are making tacit use of the Banach-Tarski decomposition theorem as a Schwinger-like source [18] [21] [34] .
exactly as should be. The preceding explanation amounts to a paradigm shift in physics where the totally empty vacuum of spacetime is taken as fundamental and everything else is derivable from it. To prove this point was a dream of Serbian American inventor N. Tesla who died in 1943 as well as Soviet physicist A. Zakharov. In fact in his later years Nobel Laureate J. Schwinger was a champion of cold fusion [12] which comes very near to our present concept of a Casimir-nano energy reactor [10] [11] . We also stress that we are making tacit use of the Banach-Tarski decomposition theorem as a Schwinger-like source [18] [21] [34] .
theorems and techniques borrowed from K-theory [6] , E-infinity mathematical theory [7] , sub-factors, knot theory, von Neumann continuous geometry [4] and in particular A. Conne’s noncommutative geometry [8] . On the whole, we hold the view that all forms of energy and matter represented by Einstein’s iconic equation E = mc2 are nothing but the zero point energy fluctuations of the real vacuum of spacetime [9] - [11] . In other words, in our dialectic philosophy we have place for a non-materialistic matter described precisely by setting theoretical
Figure 2. Julian Schwinger, Nobel Laureate in Physics and an extraordinary proponent of cold fusion. Prof. Schwinger went as far as resigning from the American Physical Society in defence of scientific freedom [12] . In the resignation letter of Prof. Schwinger he lamented what he considered censorship of science exemplified by editors of famous mainstream journals rejecting papers based upon pretentious and unfair reports by anonymous referees. On the whole Prof. Schwinger was a careful thinker and superior mathematician compared to his colleagues and co-Nobel Prize winner of the same year, the equally extraordinary Richard Feynman. The usual cheap shots like crackpot and old wood or numerologist could never be applied to this extraordinarily intelligent and super rational thinker. By being open minded like he was, Prof. Schwinger may have provoked conventional thinkers because he did not think very highly of the extensive use of Feynman’s diagrams and by introducing an alternative theory to quantum field theory known as source theory [19] which he applied similar to the present work to the Casimir effect. In fact our Banach-Tarski theorem plays in our theory the role of a Schwinger source [18] [21] .
operations [5] [8] [10] . We habitually call this for us esoteric matter, spacetime but it can be called more mathematically, an infinite dimensional and hierarchal empty set [4] - [11] . The objective of the present paper is to show how we can extract energy from this spacetime by building a nano reactor that in a sense combines Casimir effect [10] [11] with cold fusion [12] [13] . We should stress from the outset that the literature upon which the present work being based is vast and our references [1] - [20] are the minimum required for a concise presentation. In addition we give in Appendix I details of how to construct our Cantorian quantum spacetime. We draw the attention of the Reader to the fact that our Banach-Tarski sphere decomposition (Figure 1) plays in the present theory a similar role to Schwinger’s source (Figure 2) in contrast to Feynman’s diagrammatic methodology (see Figure 3) [18] [21] .
Figure 3. The Feynman graph in the Schwinger source mirror. Richard Feynman is without a trace of a doubt one of the very greatest theoretical physicists of all times. However there is equally no doubt that his graphs method over emphasized the particle picture of a quantum particle. The present author admits that by temperament and pattern of thinking, he stands nearer to Feynman than Schwinger but never the less; the present Cantorian theory stands nearer to Schwinger’s source theory. Thus it is yet another example for a theory which is far cleverer than the scientist who developed it. For more about the shortcomings of summing Feynman graphs, the reader is referred to the superb advanced textbook of Prof. Herbert M. Fried [34] .
2. The Fractal inside the Complex
In some deep sense E-infinity success in dealing with fundamental problems in high energy quantum physics and cosmology is based upon replacing complex numbers and the associated quantum probability amplitude by highly structured golden mean ring based new probability [1] [4] [5] . In this new theory which starts with a one dimensional Mauldin-Williams random Cantor point, i.e. a Cantorian [4] is a topological probability given by the inverse ratio of the Hausdorff dimension of the one dimensional continuum, i.e. its topological Menger- Urysohn dimension DT = 1 to the Hausdorff dimension of the said Cantor set, i.e. DH =
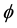 where
where


On the other hand what ever is left from the DT = 1 one-dimensional continuum after subtracting the random zero measure







and the fat measure empty Cantor set [1] [10] [11] [17]

There are various geometrical, topological and physical interpretations for these two fundamental sets. Thus the






or

where V and W are complex numbers [9] . Our next task is to show how the involved complex number can be replaced by the most irrational of all irrational numbers, namely the highly structured golden mean transfinite ring [15] . Transforming V and W as

and

and inserting in the union expression of P, one finds

For the intersectional probability one finds

In other words we have the equality of P(union) and P(intersection) which is the familiar indistinguishability condition [4] that fully explains what is normally seen as the paradoxical outcome of the famous two-slit experiment with quantum particles [4] .
We conclude that as the complex iteration leading to the famous Mandelbrot could be seen as the fractals inside the complex numbers [9] , so by the same token it is natural to replace conventional quantum mechanics by transfinite highly structured rings quantum mechanics [15] . In conclusion of this preliminary short discussion, we should note that



as shown on many previous occasions [1] [4] . A somewhat detailed discussion of quantum spacetime emerges from the pre-quantum zero set particle and pre-quantum empty set wave is given in Appendix 1. Here it is sufficient to mention on passing that quantum spacetime could be regarded within our theory as an empty pilot wave with the average bi-dimension
3. The Reinterpretation of Einstein’s E = mc2 to Mean E = (mc2/22) + mc2(21/22) and Zero Point Vacuum Fluctuation
In various previous publications a new reinterpretation of Einstein’s magnificent equation E = mc2was introduced by dissecting it to the sum of ordinary energy and the sum of dark energy density of the universe [10] [17] . It was further reasoned that the ordinary energy is the energy of the quantum particle in five dimensional Kaluza-Klein (K-K) spacetime and the dark energy being the energy of the quantum wave in the same 5D K-K spacetime [1] [10] [17] . In this section we seek to give a more intuitive explanation for the dissection as well as linking the entire theory to the zero point vacuum energy of spacetime [11] - [13] .
Let us start with the phenomenology of the wave collapse [9] . Taking any measurement in classical quantum mechanics means observing a particle and never a wave although we will of course find the tell tale sign of a wave, namely the interference pattern after the fact provided no measurement is taken [9] . In other words, the wave aspect of this wave particle duality can be observed only indirectly as interference pattern, which disappears on measurement [8] [9] [19] . Now since it is the wave that propagates in quantum spacetime (that means in the empty pilot wave space) even though it is formally a probability wave, then in the Bohmian quantum mechanics at least we can say that the quantum wave energy is the kinetic energy of propagation and that we cannot measure it unless wave non-demolition measurement instruments are invented first [1] [9] . The potential energy on the other hand is the energy of the particle that we can readily measure because it is statical and can be found easily using conventional methods [9] . Now we ask a new question, namely how can the proceeding interpretation be viewed from the point of the true persistent probability of the true vacuum of spacetime? Starting from quantum field fundamentals and the exposition of for instance J. Schwinger, this probability is given by [12] [18]

where Wo is the familiar complex vector of quantum physics [9] [12] [18] . It is a well known fact that the real part of this complex form represents the statical part of W while the imaginary part is the dynamical part [9] [12] [18] . In other words, W consists of two effects, namely a statical real one which can be measured directly as a physical quantity analogous to the ordinary energy part of E, namely E = (mc2/22) while the kinetic energy is the imaginary part of W analogous to the dark energy of E, i.e. E = mc2(21/22) [17] . We conclude that had Einstein accepted quantum mechanics and moved on to quantum field theory, he would have realized that E = mc2 means far more than anyone ever thought. It is actually the explanation of dark energy when written as [10] [17]

and goes on to explain dark matter when we incorporate the Kerr spinning singularity and arrive at the triadic division of E which takes the form [10] [17]

This is very close indeed to the results of measurements and cosmic observation that led to the COBE and accelerated cosmic expansion Nobel Prize in Physics and Cosmology [1] . Taking a bird’s eye view of the entire energetic situation, we realize how close Schwinger’s conception of persistent probability of the vacuum is to our conception of spacetime being pilot wave energy with a quantum particle.
4. Some Mathematical Prerequisites
Let us start by recalling some facts about our Cantorian spacetime [4] [10] [11] . It is described by




sis and in view of previously obtained results [1] [2] [11] , we notice immediately that



Furthermore, it cannot pass unnoticed that

topological energy

space associated with the surface of the zero set quantum particle, i.e. the empty set quantum wave. It is given as the product of the topological dark mass 5 which is the dimensions of Kaluza-Klein spacetime additive topological volume with the square of the topological Cantorian interval speed of light CT(Topological) =


5. Fusion Algebra [22] for a Casimir Gradual Implosion
What we just said in the preceding section may strike one at first glance as difficult to grasp since fusion, as we know it from a fusion bomb, i.e. hydrogen bomb requires a huge amount of heat which can be provided in practice only via a fission bomb, i.e. an atom bomb [14] . From such a perspective cold fusion would seem like an unrealistic dream that can take place in nature only on the sun and similar hot stars or in a plasma [12] [13] . However we are proposing to manipulate the situation on the far smaller energy of nano measure spacetime, which is far less ‘hot’ than the Planck or the Compton measure of elementary particles [9] . Thus we are dealing in effect with the Casimir energy part with a twist. To understand what we mean we go back to the fission weapon [14] . In this case ignition takes place automatically at a critical mass [14] . That way one uses either the gun method where two sub-critical masses are shot together or the second well known method, which is the implosion method when a shockwave changes the density of a non-critical mass suddenly making it critical [14] . Here we propose using nano particles to cause a gradual controlled low speed implosion of a heap of suitable nano particles to maximise the Casimir effect leading to a semi cold fusion on the level of the resolution of a quantum field theory of nano particles so that large amounts of the so produced far higher than usual Casimir energy which will escape to the surface of the heap can be extracted [10] - [13] . In other words, we are creating mini universes resembling moduli of a mini multiverse [9] giving us in effect a cold fusion Casimir nano energy reactor with a deep intimate connection to the four dimensional fusion algebra used by the present author to simulate a highly structured golden ring quantum field theory [10] - [13] [22] - [34] . In this regard two well known theoretical effects will affect the real physical situation. The first is the physics and mathematics of surfaces and the 96% Dvoretzky measure concentration [15] . The second is the artificial high dimensionality of fractal sphere packing [16] . In what follows we would like to expand the preceding highly condensed ideas.
6. A Preliminary Design Proposal for a Cold Fusion Casimir Nano Energy Reactor
Let us leave the mathematical modelling of our reactor aside for now and ask ourselves how we will go on to build our reactor guided by the insight we gained so far. In practical terms it will all boil down to filling a small spherical shell with a huge amount of nano particles of various size and mixing it randomly and experiment with it to find an optimal density design. We expect to extract heat from this model by joining many such spaces in a fractal tree or network resembling a spacetime matrix that is, in the end analysis, our nano reactor [10] - [13] . In the most simplistic of terms we identify the things which we have to normally eliminate from a nanotechnological devices and just do the opposite here, i.e. maximizes what we normal minimize, namely the Casimir effect.
7. The Maximal Total Energy Locked in the Fractal Kaluza-Klein Spacetime
To understand the theoretical scheme behind our design we need to understand the following. The entire topological energy density of the universe is the product of a fractal Klein-Kaluza spacetime dimension 5 +



Inserting in Newton’s formula one finds [17]

On the other hand the topological mass of dark energy m = 5 and the topological mass of ordinary energy m =






in all the time since 1915, Einstein’s beauty harboured in E the quintessence of the quantum theory dualism of wave and particle [17] . To end this section let us show how to arrive to D = 5 +


For the ground state vacuum we have to do the same for n = 0 to n = minus infinity. This is then

The total sum is thus our fractal Klein-Kaluza dimensionality

From this master expression successive reinterpretation leads to various fundamental results in an incredibly simple way. First taking on rational approximation





8. The Reasonable Effectiveness of Highly Structured Theories as the Raison D’Etre of E-Infinity Theory
Any reflective mind, whether one who occasionally uses and contributes to physical E-infinity theory or one from its inner wheels, must at a certain point ask himself why is this theory so simple mathematically and yet miraculously effective physically [1] [2] [4] . There may be more than one answer and more than one view point to explain this remarkable fact. As far as the present author is concerned, for the time being and awaiting a may be better explanation in the future, the following rationale may be partially satisfactory to a point. First E-infin- ity theory is rooted in the powerful topological global method even tough it gives numerical exact results [4] . However these exact solutions and the associated exact numeric are basically due to the involved highly structured nature of the theory. Our second point is that there may be at least two main aspects of the preceding conclusion, namely the golden mean highly structured rings [6] upon which our computation is completely founded. In addition an extension of this well known aspect of E-infinity mathematical theory, the physical E-infinity Cantorian spacetime theory is itself highly structured conceptually. This highly structured physical conception is what allows us to move from one physical aspect to another with almost a miraculous ease and simplicity. On the most fundamental level









9. Constructing Spacetime from Quantum Particles and Quantum Wave
In the following we give the quintessence of a non-perturbative quantum relativity theory. We start from von Neumann-Connes’ dimensional function for the x quotient noncommutative space [8] of which the Klein-Pen- rose fractal tiling universe [8] [9] is a generic quasi manifold

where


D º D(T,H) where T is the Hausdorff dimension of a bijected Menger-Urysohn topological dimension T. Consequently for the zero set pre-quantum particle one finds [1] [11]

On the other hand the quantum wave, which is the surface of the quantum particle, is given by the cobordism empty set



Proceeding in the same manner one finds an infinite number of successive empty and emptier still sets given by [1] [4] [11]

Adding to this the quantum pre-particle





which for n = 3 gives us the same previous result, namely

Now we can contemplate two possibilities to gauge



The second possibility is to gauge


where





This is simply the dimensionality of a fractal Witten’s M-theory [4] [7] or a fractal super gravity spacetime. This fractal M-theory clearly supports the particle-wave duality of quantum mechanics. It is now extremely insightful to note the following: since the pre-quantum wave





10. Feynman Diagrams from a Source View Point
The attentive reader must have realized by now that the viewpoint behind the present work is much nearer to Schwinger’s source theory than it is to Feynman (see Figure 2 and Figure 3). This is by no means surprizing. Feynman’s diagrams, apart of anything else, have an inbuilt bias towards the particle aspect of the quantum. Here however we presented a fairly balanced particle-wave picture. In fact we say ‘fairly’ because the wave is on our view nearer to spacetime itself being both empty sets and the only difference is the degree of emptiness of this empty set. By contrast the particle is a non-empty zero set. Elaborating further on the Feynman graphs method and referring to the above comments and the legend of Figure 3 as well as our calculation in Section 9, it is well known that summing over subset of Feynman graphs that include infinite numbers of graphs. That way it is impossible to find an exact solution or in fact determine accurately the magnitude of error. This stands in marked contrast to Schwinger’s non-perturbative approach as well as our method as presented for instance in the short exact analysis given in Section 9. To sum up and put it in a nutshell, despite all the difference E-infinity theory comes much nearer to the functional formulation of Schwinger and Fradkin than to the very popular method of Feynman [34] . That incidentally is how we could tackle and solve the problem of dark energy and dark matter.
11. Conclusion
We presented in embryonic form a non-perturbative quantum relativity theory. Subsequently, a spacetime zero point vacuum nano reactor was outlined conceptually based mainly but not exclusively on the said theory as well as quantum set theory [19] and E-infinity theory [4] [6] [11] . Other subjects and theories played a major role in the present work, namely nanotechnology, K-theory, n-category theory, Dvoretzky’s theorem, sphere packing, Schwinger source theory and 4 dimensional fusion algebra of topological quantum field theory [22] - [33] . The crucial step in the actual design was the realization that spacetime itself was virtually an infinite reservoir of cosmic energy and that the experimentally confirmed Casimir effect was but the local manifestation of fractal Cantorianspacetime fluctuation





Cite this paper
Mohamed S. ElNaschie, (2015) On a Non-Perturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal. Open Journal of Applied Sciences,05,313-324. doi: 10.4236/ojapps.2015.57032
References
- 1. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718.
http://dx.doi.org/10.1007/s10773-014-2123-8 - 2. Auffray, J.-P. (2014) Quantum Meteorites: An Extemporaneous Description of the System of the World. Journal of Modern Physics, 6, 878-889.
http://dx.doi.org/10.4236/jmp.2015.67092 - 3. Nottale, L. (1996) Scale Relativity and Fractal Spacetime: Application to Quantum Physics, Cosmology and Chaotic Systems. Chaos, Solitons & Fractals, 7, 877-938.
http://dx.doi.org/10.1016/0960-0779(96)00002-1 - 4. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
http://dx.doi.org/10.1016/S0960-0779(03)00278-9 - 5. El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155.
http://dx.doi.org/10.1134/S0202289313030031 - 6. Witten, E. (1998) D-Branes and K-Theory. Journal of High Energy Physics, 12, 1-35.
http://dx.doi.org/10.1088/1126-6708/1998/01/001 - 7. May, J.P. (1977) E-Infinity Ring Spaces and E-Infinity Spectra. Lecture Notes in Mathematics, Springer, Berlin.
- 8. Connes, A. (2000) Noncommutative Geometry Year 2000. Geometric and Functional Analysis. Special Volume, Birkhäuser-Verlag, 481-599.
http://dx.doi.org/10.1007/978-3-0346-0425-3_3 - 9. Penrose, R. (2004) The Road to Reality. Jonathan Cape, London.
- 10. El Naschie, M.S. (2015) Kerr Black Hole Geometry Leading to Dark Matter and Dark Energy via E-Infinity Theory and the Possibility of Nano Spacetime Singularity Reactor. Natural Science, 7, 210-225. http://dx.doi.org/10.4236/ns.2015.74024
- 11. El Naschie, M.S. (2015) The Casimir topological Effect and a Proposal for a Casimir-Dark Energy Nano Reactor. World Journal of Nano Science & Engineering, 5, 26-33.
http://dx.doi.org/10.4236/wjnse.2015.51004 - 12. Schwinger, J. (2014-2015) Cold Fusion Theory: A Brief History of Mine. A Talk Read in an Evening Session by Eugene Mallove at the Fourth International Conference on Cold Fusion ICCF4, Maui, December 1994, Printed Online by Infinity Energy—The Magazine of New Energy Science & Technology. www.infinite-energy.com/iemagazine1/colfusthe-html
- 13. Jiang, X.L., Zhou, X.P. and Peng, W.M. (2014) Extraction of Clean and Cheap Energy from Vacuum. Materials for Renewable Energy & Environment, 2, 467-471.
- 14. El Naschie, M.S. (1999) From Implosion to Fractal Spheres. A Brief Account of the Historical Development of Scientific Ideas Leading to the Trinity Test and Beyond. Chaos, Solitons & Fractals, 10, 1955-1965. http://dx.doi.org/10.1016/S0960-0779(99)00030-2
- 15. El Naschie, M.S. (2015) Banach Spacetime-Like Dvoretzky Volume Concentration as Cosmic Holographic Dark Energy. International Journal of High Energy Physics, 2, 13-21.
http://dx.doi.org/10.11648/j.ijhep.20150201.12 - 16. El Naschie, M.S. (2005) On 336 Kissing Spheres in 10 Dimensions, 528 P-Brane States in 11 Dimensions and the 60 Elementary Particles of the Standard Model. Chaos, Solitons & Fractals, 24, 337-457. http://dx.doi.org/10.1016/j.chaos.2004.09.071
- 17. El Naschie, Mohamed S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entanglement Origin. Journal of Quantum Information Science, 4, 284-291. http://dx.doi.org/10.4236/jqis.2014.44023
- 18. Schwinger, J. (1975) Casimir Effect in Source Theory. Letters in Mathematical Physics, 1, 43-47. http://dx.doi.org/10.1007/BF00405585
- 19. Finkelstein, D. (1996) Quantum Relativity. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-642-60936-7 - 20. Hooft, G. (2014) The Cellular Automata Interpretation of Quantum Mechanics. A View on the Quantum Nature of Our Universe, Compulsory or Impossible? arXiv:1405.1548v2
- 21. El Naschie, M.S. (1995) Banach-Tarski Theorem and Cantorian Micro Spacetime. Chaos, Solitons & Fractals, 5, 1503-1508. http://dx.doi.org/10.1016/0960-0779(95)00052-6
- 22. El Naschie, M.S. (2009) Wild Topology, Hyperbolic Geometry and Fusion Algebra of High Energy Particle Physics. Chaos, Solitons & Fractals, 13, 1935-1945.
http://dx.doi.org/10.1016/S0960-0779(01)00242-9 - 23. Gillet, H. (1981) Riemann-Roch Theorem for Higher Algebraic K-Theory. Advances in Mathematics, 40, 203-289. http://dx.doi.org/10.1016/S0001-8708(81)80006-0
- 24. Kodiyalam, V. and Saunder, V. (2001) Topological Quantum Field Theories from Subfactors. Chapman & Hall/CRC, Bacaraton and London.
- 25. Witten, E. (1988) Topological Quantum Field Theory. Communications in Mathematical Physics, 117, 353-386. http://dx.doi.org/10.1007/BF01223371
- 26. Baez, J.C. and Dolan, J. (1988) Higher-Dimensional Algebra III: N-Categories and the Algebra of Opetopes. Advances in Mathematics, 135, 145-206.
http://dx.doi.org/10.1006/aima.1997.1695 - 27. May, J.P. (2009) What Precisely Are E-Infinity Rings and E-Infinity Spectra. arXiv: 0903.2813v1
- 28. Ketov, S.V. (1995) Conformal Field Theory. World Scientific, Singapore.
- 29. Duplantier, B. and Rivasseau, V. (2003) Poincaré Seminar 2002. Vacuum Energy—Renormalization. Birkhauser, Ba- sel.
- 30. Saller, H. (2006) Operational Quantum Theory I and II. Springer, Heidelberg.
- 31. Milonni, P.W. (1994) The Quantum Vacuum, An Introduction to Quantum Electrodynamics. Academic Press, Boston.
- 32. Connes, A. and Marcolli, M. (2008) Noncommutative Geometry, Quantum Fields and Motives. American Mathematical Society Hindustan Book Agency.
- 33. Stephenson, K. (2005) Introduction to Circle Packing. Cambridge University Press, Cambridge.
- 34. Fried, H.M. (2014) Modern Functional Quantum Field Theory. World Scientific, Singapore.
http://dx.doi.org/10.1142/8544




