Open Journal of Applied Sciences
Vol.05 No.08(2015), Article ID:58545,12 pages
10.4236/ojapps.2015.58041
Preparation of Chitosan Copper Complexes: Molecular Dynamic Studies of Chitosan and Chitosan Copper Complexes
Ayman S. ELmezayyen*, Fikry M. Reicha
Biological Advanced Materials, Department of Physics, Faculty of Science, Mansoura University, Mansoura, Egypt
Email: *ayman_ss@mans.edu.eg, fikry_reicha@mans.edu.eg
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2015; accepted 1 August 2015; published 4 August 2015
ABSTRACT
This work studied the effect of copper ions concentration chelated by functional groups in chitosan on its molecular dynamic. Chitosan Copper complexes prepared having different copper concentrations by the electrochemical oxidation technique in aqueous-acetic acid medium. It was carried out at constant voltage (2 volt.) at room temperature at different electro-oxidation time. The result of partial elemental analysis and XRD studies of chitosan copper complexes compared with chitosan confirmed that the percentage composition of the complexes were found to be depend on the time of electrolysis which is in good agreement with our previous work. Interpretation of the effect of copper ions concentration on molecular motion of chitosan studied using dielectric spectroscopy, the results showed that dielectric constant of chitosan is higher than that of chitosan copper complexes. This may be attributed to the relatively fast segmental motion of chitosan chain slowed down by complexation with copper ions of all complex samples. Calculated activation energy from Arrhenius variation showed increase in value with increasing the copper concentration and all in the range that required for ionic conduction. Temperature dependence part of dielectric parameters gives very useful representation in the glass transition temperature determination.
Keywords:
Chitosan Complexes, Molecular Dynamic, Glass Transition Temperature

1. Introduction
Chitosan and partially acetylated chitosan are more reactive than chitin because they possess a number of functional groups such as (OH, NHCOCH3 and NH2) to which metal ions can bind either by chemical or by physical adsorption. The presence of large number of oxygen and nitrogen atoms, in particular, having lone pair electrons make the adsorption of metal cations in neutral or moderately acidic media available. However, the NH2 groups react much more rapidly than the OH moieties towards salts [1] . Chitosan is a well-known sorbent, effective in the uptake of metal ions, since the amine groups on the chitosan chain can serve as chelating sites for metals. The mechanism by which metal ions are bound by chitosan involves attachment of these ions to?NH2 groups [2] . Also; it has been shown that the mechanism of metal uptake by chitosan is a combination of adsorption, ion exchange, and chelating [3] .
Recent researches that pay attention to the biological activities of chitosan metal complexes, show that chitosan-metal complexes are promising candidate for biomedical agents that can be used in many biological applications. Chitosan-metal complexes, including Cu(II ), Zn (II), Fe(III) and Ag(I) show wide spectrum antimicrobial activity, anti-fungi, highest anti-tumor activity and low toxicity [4] [5] .
In our previous work [6] , we interpreted the formation of copper chitosan complexes using FTIR and Far- FTIR, UV/visible, XRD, ESR, Swelling ratio, Thermogravimetric (TGA) analysis, relative viscosity measurements and Biological evaluation of copper chitosan samples.
Herein, the objective of this work is to confirm the formation of chitosan-metal complexes and study the effect of copper ion concentration on the molecular motion of chitosan using dielectric spectroscopy.
2. Experimental
2.1. Materials
Chitosan powder, Mw = 600,000 g/mol and degree of deacetylation (DD) is 75% (Aldrich chemical co.), Acetic acid of analytical grade, De-ionized water, Copper plates (20 mm, 40 mm, 2 mm), Sigma-Aldrich of purity 99.995%, used as working electrode (anode). Platinum rectangular sheets (20 mm, 40 mm, 0.5 mm), Sigma-Al- drich, used as counter electrode (cathode).
2.2. Procedure for Copper Complex Preparation
The copper chitosan complexes were prepared by the electrochemical oxidation of the copper metal in an aqueous acidic medium.
In the present preparation the electrochemical oxidation was carried out at constant potential of 2V using potentiosatatic method in a one compartment electrochemical cell.
Electrolytic Solutions were prepared by dissolving 1 wt% chitosan into 2% acetic acid, solution placed on magnetic stirrer for 24 hrs.
The experimental setup used for preparation of copper chitosan consists of Copper strip (anode) and Platinum strip (cathode) was immersed in the electrolytic solution suspended at a distance 5 cm from each other by Platinum wires. The Platinum wires were connected to a suitable variable resistor and constant-voltage power supply (Model 1030A, U.S.A). Nitrogen gas current was flushed into the electrolyte during all the preparation. The temperature was held constant at 25˚C by using a circular water bath (VEB MLW, Type U4; GDR).
Preliminary experiments were carried out to different electro-oxidation time (10 hrs―CS-(1N), 2.5 days― CS-(2N) and 5 days―CS-(3N)), the solution was centrifuged at speed (10,000 rpm for 30 min.), and filtered in order to remove any debris.
The complexes were casted onto plastic petri dishes of diameter 120 mm and dried for 72 h at ambient temperature. The thick films were peeled off from the dishes and subsequently allowed to dry for more than one week in an oven at 50˚C.
2.3. Material Characterization Techniques
2.3.1. Elemental Analysis
The weight percentage of Chitosan copper complexes was determined by means of elemental analysis using CHN elemental analyzer (Model 2400 Perkin Elmer USA).
2.3.2. X-Ray Powder Diffraction (XRPD) Analyses
The diffraction patterns were obtained using an X-ray powder diffractometer (BrukerAxs D8 Advance, Germany) with Cu Kα target (Ni filter), wavelength (k) = 1.54 Å. The voltage was 40 KV and the current intensity was 30 mA. The 2θ angle was scanned between 4˚ and 40˚, the XRPD runs carried out at scanning speed of 2θ = 2˚/min.
2.3.3. Electrical Properties Measurements
The electrical conductivity and dielectric measurements were carried out on dried samples in the form of rectangular shape (2 × 2 cm) and thickness (d) of the samples CS, CS-(1N), CS-(2N) and CS-(3N): 0.036, 0.04, 0.038 and 0.045 cm respectively, measured by digital micrometer. The common circular area of diameter 1 cm on the sample surfaces was rubbed with silver past to achieve better electrode contact. A double stage rotary pump (Edward MLW, type DS8, GDR) evacuated the cell to a pressure of about 10−3 torr. The cell was evacuated for at least 18 hours maintaining the temperature at 90˚C after inserting the sample into it to ensure minimum humidity, then cooling to room temperature without corruption the evacuation. Stanford research systems model SR830 DSP lock-in amplifier, USA, was used for collecting data (frequency range 50 Hz to 100 kHz with accuracy 25 ppm + 30 μHz and resolution 4.5 digits or 0.1 m Hz, phase resolution 0.010, amplitude 4 mVrms to 5 Vrms with 2 mV resolution and 1% accuracy).
3. Results and Discussion
3.1. Elemental Analysis
Carbon (C), Hydrogen (H), Nitrogen (N) and metallic residue (M.R.) content of chitosan copper complexes Table 1 showed that the copper content increases by increasing the preparation time i.e. by increasing the dissolution of the anode. The composition % was 1:17.8 (Cu: glucoseamine unit) for highly complexed sample denoted CS-(3N), 1:37.31 for mild CS-(2N), and 1:181.8 for low copper concentration CS-(1N) [6] .
3.2. X-Ray Diffraction
The morphology of the copper chitosan complexes was studied in a facile manner by XRD, which afforded an easy tool to evaluate the extent of binding. Thus a study of XRD is in itself a powerful tool to study the extent of metal binding by polymer ligand where the key functional groups are extensively utilized in binding, thereby disrupting the original polymer structure and the consequent changes in the XRD spectra.
Figure 1 shows the XRD patterns of CS, the complexes [CS-(1N), CS-(2N), and CS-(3N)]. Diffractograph of chitosan consists of three characteristic broad peaks at 2θ = 9.57, 15 and 20.33˚ come from the amorphous region [7] . While the characteristic crystalline peak, usually appear at 2θ > 23˚ are absent. This is in agreement with the reported results [8] - [11] in which, they referred the degree of crystallinity to the degree of deacetylation and molecular weight, higher degree of deacetylation lower molecular weight arises to higher degree of crystallinity. The Peak observed at around 15˚ has been attributed to the anhydrous crystal lattice [10] . Moreover, peak in the range 9 - 13 refers to the disordered portions of the polymer in the C-2 amino group [7] . The second broad region from 2θ = 10˚ - 23˚ are attributed to the hydrophilic pockets in the polymer, i.e. a hydroxyl alcohols from both C6 and the glucosamine monomeric ring structure and amide groups on the backbone of chitosan.
Comparing the diffractograph of CS with Cs-(3N) sample, the first broad signal found in XRD pattern for chitosan disappeared indicating that metal ions are complexed with NH2 groups which form bridge model. The second peak at 2θ = 15˚ in chitosan is also disappeared, while the intensity of signal at 2θ = 20.33˚ significantly reduced and becomes broad. This indicates a great deal of these copper ions favors interaction with the amor- phous region of chitosan [11] to form a bridge coordination between NH2 and OH groups and pendant or absorbed in the amorphous pockets.
Table 1. Element analysis data of chitosan and its complexes.
Figure 1. XRD spectra of CS and its complexes.
The XRD pattern of CS-(1N) and CS-(2N) samples showed that the position of amorphous peaks unaltered while their intensities and broadening affected.
Adding, from our previous work [6] , chitosan bonded with Cu ions through the NH2 in pendant model and through NH2 and OH groups in the bridged model. The pendant model may proceed through the following ion exchange mechanism:
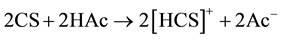


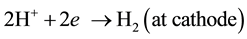
3.3. Dielectric Properties Response
Studying of dielectric constant, dielectric loss, dissipation factor and electric modulus as a function of temperature and frequencies is one of the most convenient and sensitive methods of studying the polymer structure [12] .
3.3.1. Frequency Dependence Part
1) Dielectric constant and dielectric loss frequency dependence
The dielectric spectra of chitosan and chitosan copper complexes were collected in ascending temperature steps starting in the frequency range (102 Hz to 105 Hz) as shown in Figure 2. It exhibits the representative frequency dependence of the real part, ε'(ω), and the imaginary part, ε''(ω) of the complex dielectric permittivity. The frequency dependence of dielectric spectra shows interesting characteristic features.
For all samples, one observes that the real part of the permittivity ε'(ω) at high frequencies approaches a limiting constant value,
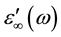 periodic reversal of the electric field occurs so fast that there is no excess ion diffusion in the direction of the field. With decreasing frequency ε'(ω) increases, and a drastically increase takes place at very low frequency at high temperatures regions indicating that electrode polarization and space charge effects have occurred confirming non-Debye dependence [13] [14] . Variation of dielectric constant with frequency can be illustrated by plotting ε'(ω) versus Log (F) Figure 3 at fixed temperature (413 K). It clearly seen that, dielectric constant of chitosan is very higher than that of all complex samples. This may be attributed to the relatively fast segmental motion of chitosan chain slow down by complexation with copper ions of all complex samples. Then ε'(ω) shows a tendency of leveling off to a plateau,
periodic reversal of the electric field occurs so fast that there is no excess ion diffusion in the direction of the field. With decreasing frequency ε'(ω) increases, and a drastically increase takes place at very low frequency at high temperatures regions indicating that electrode polarization and space charge effects have occurred confirming non-Debye dependence [13] [14] . Variation of dielectric constant with frequency can be illustrated by plotting ε'(ω) versus Log (F) Figure 3 at fixed temperature (413 K). It clearly seen that, dielectric constant of chitosan is very higher than that of all complex samples. This may be attributed to the relatively fast segmental motion of chitosan chain slow down by complexation with copper ions of all complex samples. Then ε'(ω) shows a tendency of leveling off to a plateau,
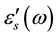 , Curves representing dielectric loss e''(w) as a function of frequency at different temperatures exhibit a relaxation peaks which shifts to higher frequencies as temperature increases, which is thermally activated process. In general, a simple thermally activated
, Curves representing dielectric loss e''(w) as a function of frequency at different temperatures exhibit a relaxation peaks which shifts to higher frequencies as temperature increases, which is thermally activated process. In general, a simple thermally activated
Figure 2. The real (ε') and imaginary (ε") parts of dielectric permittivity spectra at different temperatures for CS, CS-(1N), CS-(2N) and CS-(3N).
Figure 3. Variation of real parts of dielectric permittivity (ε') as a function of frequency at fixed temperature (413 K) for all samples.
process will follow the Arrhenius behavior:
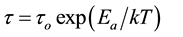 (1)
(1)
where Ea is the activation energy and τo the relaxation time for temperature tends to infinity, i.e., the relaxation time in the absence of energy barriers. In our samples such a plot was found to be difficult may be due to the effect of heterogeneity (Maxwell-Wagner-Sillars (MWS)) and/or electrode polarization. So activation energy for this process would be calculated well by suppressing the electrode polarization using imaginary part of the electric modulus M''(ω).
2) Dissipation Factor tan(δ) Frequency Dependence
A very important quantity is the dielectric loss tangent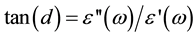 , which measures directly the
, which measures directly the
phase difference due to loss of energy within a sample at a particular frequency. Figure 4 shows the variation of tangent loss with frequency of chitosan and chitosan copper complex films for different temperatures. The loss spectra characterized by peak suggests the presence of relaxing dipoles in all the samples. The maximum of the relaxation peak are slightly increases and deviated to higher frequency as the temperature increases from room temperature up to about 433 K indicating a thermally activated process, which speed up the segmental motion by increasing the available free volume. It is evidenced by the peak shifting towards higher frequency side, thereby reducing the relaxation time. Finally, maximum of the spectra deviate to lower frequency after temperature 433 k, which appear as a peak in the plot between tan(δ) versus temperature.
The relaxation parameters can be obtained from the study of tan(δ) as a function of frequency. For maximum dielectric loss at a particular temperature, the absorption peak is described by the relation
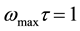 where τ is the relaxation time and ω is the angular frequency of the applied signal. The relaxation parameters are tabulated in Table 2. The occurrence of relaxation time is the result of the efforts carried out by ionic charge carriers within the polymer material to obey the change in the direction of applied field. The shift of (tanδ)max towards high frequency with increasing temperature indicates that relaxation time decreases with temperature. A simple thermally activated process will follow the Arrhenius behavior equation (1). The Arrhenius plot of
where τ is the relaxation time and ω is the angular frequency of the applied signal. The relaxation parameters are tabulated in Table 2. The occurrence of relaxation time is the result of the efforts carried out by ionic charge carriers within the polymer material to obey the change in the direction of applied field. The shift of (tanδ)max towards high frequency with increasing temperature indicates that relaxation time decreases with temperature. A simple thermally activated process will follow the Arrhenius behavior equation (1). The Arrhenius plot of
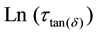 vs. 1000/T as shown in Figure 5, then gives an activation energy of
vs. 1000/T as shown in Figure 5, then gives an activation energy of
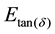 and a value for
and a value for
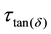 as seen in Table 2.
as seen in Table 2.
3) Electric modulus frequency dependence
Further analysis of the dielectric behavior would be more successfully achieved using dielectric moduli, which suppresses the effects of electrode polarization. The electric modulus is the reciprocal of the permittivity. Although it was originally introduced by Macedo [15] to study space charge relaxation phenomena, M* representation is now widely used to analyze ionic conductivities [16] Physically, the electric modulus corresponds to
Figure 4. Variation of the loss factor tan(δ) as a function of frequency at various temperatures for CS, CS-(1N), CS-(2N) and CS-(3N).
Table 2. Relaxation parameters of all samples (calculated from dissipation factor).
Figure 5. Arrhenius variation of the relaxation time with temperature for all samples.
the relaxation of the electric field in the material when the electric displacement remains constant, so that the electric modulus represents the real dielectric relaxation process.
The real M′(ω) and imaginary M″(ω) parts of the electric modulus as a function frequency at different temperatures of chitosan and chitosan Copper complexes are displayed in Figure 6. The conductivity behavior in the frequency domain is more conveniently interpreted in terms of conductivity relaxation time, τo, using electrical modulus (M*) representation. The M* representation is now widely used to analyze ionic conductivities by associating a conductivity relaxation time with the ionic process [17] . From Figures, it is obvious that at lower frequencies M′ values are very small, tend to be zero indicating the removal of electrode polarization [18] [19] , while the increase of M′ with increasing frequency and reaching a maximum value M∞ at high frequency, may be due to the distribution of relaxation processes over a range of frequencies [20] . The observed dispersion is mainly due to conductivity relaxation spreading over a range of frequencies and indicates the presence of a relaxation time, which should be accompanied by a loss peak in the diagram of the imaginary part of electric modulus versus frequency. The absence of peak in M′ diagram is due to the fact that M′ in complex electric modulus (M*) is equivalent to ε′ in complex permittivity (ε*) i.e. M′ represents the ability of the material to store the energy. The reduction in the values of M′ at increasing temperature results from the increase in the mobility of the polymer segment and charge carriers with the temperature, it is well known that the orientation of the charge carriers and molecular dipoles becomes easier at high temperatures. The formation of loss peaks is clearly observed in Figure 6. It is obvious that at lower frequencies M″ approach to zero indicating the fact that the electrode polarization phenomena make a negligible contribution [21] , where the electrode polarization may causes an apparent increase in the dielectric constant at low frequencies. The anomaly originates in a high-im- pedance layer on the electrode surface. This may be caused by imperfect contact between the metal electrode surface and the specimen, aggravated by the accumulation of the products of electrolysis etc. At low frequencies there is sufficient time for any slight conduction through the specimen to transfer all the applied field across the very thin electrode layers and the result is an enormous increase in the measured capacitance [22] . However, at high frequencies well-defined peaks are observed, the broad and asymmetric of peaks on both sides of the maxima predicts the non-Debye behavior. The region on the left of the peak determines the range in which charge carriers are mobile over long distances, while region to the right is where carriers are confined to potential wells being mobile over short distance [19] . The frequency associated with each peak is known as relaxation frequency and gives the most probable conductivity relaxation time τo for ions. The reciprocal temperature variation of log (f max) is shown in Figure 7. The relaxation peak is thermally activated satisfies the Arrhenius behavior
3.3.2. Temperature Dependence of Dielectric Parameters and Detection of Tg
The temperature dependences of the dielectric constant ε'(ω), dissipation factor tan(δ) and real electric modulus
Figure 6. Frequency dependence of (a) the real part, M', and (b) the imaginary part, M'', of the electric modulus at different temperature of CS, CS-(1N), CS-(2N) and CS-(3N).
Table 3. The variation of the activation energy, Ea(eV), and the pre-exponential factor, τo (Sec), for all samples (calculated from electric modulus).
Figure 7. Arrhenius variation of the relaxation time with temperature for all samples.
M'(ω), for various frequencies are shown in Figures 8(a)-(d), Figures 9(a)-(d) and Figures 10(a)-(d). We notice that there is a local maximum peak in ε'(ω) and tan(δ) parameters while lower maximum peak in M'(ω) at temperature (Tmax), which we believe corresponds to the glass transition temperature. At lower temperature, as the dipoles are rigidly fixed in the dielectric, the field can’t change the condition of dipoles. As the temperature increases, the dipoles comparatively become free and they respond to the applied electric field. Thus polarization increased and hence dielectric constant and dissipation factor is also increased with the increase of temperature in neighboring of glass transition temperature (Tg). On further increase in temperature, the chaotic thermal oscillation intensifies and therefore degree of order of orientation is diminishing. In comparison between chitosan and chitosan copper chitosan samples, with increasing the copper ion concentration, it confirmed that; drastically decrease in dielectric constant, corresponding to increase in the electric modulus (the reciprocal of the dielectric constant) attributed to the chelation of copper ions by chitosan functional groups which play the role of reducing of the segmental motion content under the effect of the electric field, corresponding to decrease in the electrical potential energy dissipated in the materials, as shown in dissipation factor plots.
3.3.3. Argand Plot Analysis
The study of Argand plot at different temperatures can be used to demonstrate the nature of relaxation processes in the present polymer. Figures 11(a)-(d) show the temperature dependence of Argand plots for all samples, it is observed that the curves of Argand plot are incomplete half semicircle which cannot be explained by Debye model (i.e., single relaxation time). In this case a distribution of relaxation time is necessary to interpret the experimental data especially in polymers. Many reasons exist for the relaxation times to be distributed in solids, such as polar groups, hopping, space charge polarization and/or inhomogeneities [23] . Our Argand plots appeared as deformed arcs at low temperature with increasing temperature the radii of this arc increases. This can be ascribed to that the orientation of the charge carriers and molecular dipoles becomes easier at high temperatures.
4. Conclusion
Chitosan copper complexes were prepared using electrochemical oxidation method, and the properties of the complexes were studied. The results showed that copper concentration increased with the electro-oxidation time. Dielectric measurement as a function of temperature and frequency showed that dielectric constant of chitosan is very higher than that of all complex samples. This may be attributed to the relatively fast segmental motion of chitosan chain slowed down by complexation with copper ions of all complex samples. From temperature depen-
Figure 8. Dielectric constant (ε') versus temperature for; (a) CS; (b) CS-(1N); (c) CS-(2N); and (d) CS-(3N).
Figure 9. Dissipation factor (Tanδ) versus temperature for (a) CS; (b) CS-(1N); (c) CS- (2N); and (d) CS-(3N).
dence of dielectric parameters, We notice that there is a local maximum peak in ε'(ω) and tan(δ) parameters while lower maximum peak in M' at temperature (Tmax), which corresponding to the glass transition temperature,
Figure 10. Variation of real part of electric modulus (M') versus temperature for; (a) chitosan (CS); (b) CS-(1N); (c) CS- (2N); and (d) CS-(3N).
Figure 11. (a) to (d)) Cole-Cole Plots of (a) chitosan CS; (b) CS-(1N); (c) CS-(2N); (d) CS-(3N).
as the temperature increases, the dipoles comparatively become free and they respond to the applied electric field. Thus polarization increased and hence dielectric constant and dissipation factor is also increased with the increase of temperature in neighboring of glass transition temperature (Tg). On further increase in temperature, the chaotic thermal oscillation intensifies and therefore degree of order of orientation is diminishing.
Cite this paper
Ayman S.ELmezayyen,Fikry M.Reicha, (2015) Preparation of Chitosan Copper Complexes: Molecular Dynamic Studies of Chitosan and Chitosan Copper Complexes. Open Journal of Applied Sciences,05,415-427. doi: 10.4236/ojapps.2015.58041
References
- 1. Guibal, E. (2004) Interactions of Metal Ions with Chitosan-Based Sorbents: A Review. Separation Science and Technology, 38, 43-47.
http://dx.doi.org/10.1016/j.seppur.2003.10.004 - 2. Juang, R., Tseng, R., Wu, F. and Lee, S.(1997) Adsorption Behavior of Reactive Dyes from Aqueous Solutions on Chitosan. Journal of Chemical Technology & Biotechnology, 70, 391-399.
http://dx.doi.org/10.1002/(SICI)1097-4660(199712)70:4<391::AID-JCTB792>3.0.CO;2-V - 3. Vold, I., Varum,K., Guibal, E. and Smidsrod, O. (2003) Binding of Ions to Chitosan—Selectivity Studies. Carbohydrate Polymers, 54, 471-477.
http://dx.doi.org/10.1016/j.carbpol.2003.07.001 - 4. Zheng, Y., Wang, Y., Zhang, W. and Du, M. (2006) Preparation of Chitosan—Copper Complexes and Their Antitumor Activity. Bioorganic & Medicinal Chemistry Letters, 16, 4127-4129. http://dx.doi.org/10.1016/j.bmcl.2006.04.077
- 5. Coleman, N., Bishop, A., Booth, S. and Nicholoson, J. (2009) Ag+- and Zn2+-Exchange Kinetics and Antimicrobial Properties of 11Å Tobermorites. Journal of the European Ceramic Society, 29, 1109-1117. http://dx.doi.org/10.1016/j.jeurceramsoc.2008.08.015
- 6. Reicha, F., Shebl, A., Badria, F. and EL-Asmy, A. (2012) Electrochemical Synthesis, Characterization and Biological Activity of Chitosan Metal Complexes. International Journal of Basic and Applied Chemical Sciences, 2, 7-22.
- 7. Webster, A., Halling, M. and Grant, D. (2007) Metal Complexation of Chitosan and Its Glutaraldehyde Cross-Linked Derivative. Carbohydrate Research, 342, 1189-1201.
http://dx.doi.org/10.1016/j.carres.2007.03.008 - 8. Yin, X., Zhang, X., Lin, Q., Feng, Y. and Zhang, Q. (2004) Metal-Coordinating Controlled Oxidative Degradation of Chitosan and Antioxidant Activity of Chitosan-Metal Complex. ARKIVOC, 2004, 66-78. http://dx.doi.org/10.3998/ark.5550190.0005.910
- 9. Trimukhe, K. and Varma, A.(2008) A Morphological Study of Heavy Metal Complexes of Chitosan and Crosslinkedchitosans by SEM and WAXRD. Carbohydrate Polymers, 71, 698-702. http://dx.doi.org/10.1016/j.carbpol.2007.07.010
- 10. Ogawa, K. (1991) Effect of Heating and Aqueous Suspension of Chitosan on the Crystallinity and Polymorphs. Agricultural and Biological Chemistry, 55, 2375-2379.
http://dx.doi.org/10.1271/bbb1961.55.2375 - 11. Schmuhl, R., Kreig, H. and Kiezer, K. (2001) Adsorption of Cu (II) and Cr (VI) Ions by Chitosan: Kinetics and Equilibrium Studies. Water, 27, 1-8.
- 12. Scott, A., Curtis, D. and Auritzenandj, A.D. (1962) Dielectric Properties of Semicrystalline Polychlorotrifluoroethylene. Journal of Research of the National Bureau of Standard, 66, 269-305. http://dx.doi.org/10.6028/jres.066A.028
- 13. Qian, X., Gu, N., Cheng, Z., Yang, X., Wang, E. and Dong, S. (2001) Impedance Study of (PEO)10LiCIO4-Al2o3 Co- mpsite Polymer Electrolyte with Blocking Electrodes. Electrochimica Acta, 46, 1829-1836. http://dx.doi.org/10.1016/S0013-4686(00)00723-4
- 14. Govindaraj, G., Baskaran, N., Shahi, K. and Monoravi, P. (1995) Preparation, Conductivity, Complex Permittivity and Electric Modulus in AgI-Ag2O-SeO3-MoO3. Solid State Ionics, 76, 47-55. http://dx.doi.org/10.1016/0167-2738(94)00204-6
- 15. Howell, F.S., Bose, R.A., Macedo, P.B. and Moynihan, C.T. (1974) Electrical Relaxation in a Glass Forming Molten Salt. The Journal of Physical Chemistry, 78, 639-648.
- 16. Angell, C. (1990) Dynamic Process in Ionic Glass. Chemical Reviews, 90, 523-542.
http://dx.doi.org/10.1021/cr00101a006 - 17. Pradhan, D., Choudhary, R. and Samantaray, B. (2008) Studies of Structural, Thermal and Electrical Behavior of Polymer Nanocomposite Electrolytes. Express Polymer Letters, 2, 630-638.
- 18. Yakuphanoglu, F. (2007) Electrical Conductivity and Electrical Modulus Properties of α, ω-Dihexylsexithiophene Organic Semiconductor. Physica B: Condensed Matter, 393, 139-142. http://dx.doi.org/10.1016/j.physb.2006.12.075
- 19. Dutta, A., Sinha, T., Jena, P. and Adak, S. (2008) AC Conductivity and Dielectric Relaxation in Ionically Conducting Soda-Lime-Silicate Glasses. Journal of Non-Crystalline Solids, 354, 3952-3957. http://dx.doi.org/10.1016/j.jnoncrysol.2008.05.028
- 20. Patro, L. and Hariharan, K. (2009) AC Conductivity and Scaling Studies of Polycrystalline SnF2. Materials Chemistry and Physics, 116, 81-87.
- 21. Patro, L. and Hariharan, K. (2009) Frequency Dependent Conduction Characteristics of Mechanochemically Synthesized NaSn2F5. Materials Science and Engineering: B, 162, 173-178. http://dx.doi.org/10.1016/j.mseb.2009.04.003
- 22. Blythe, T. and Bloor, D. (1979) Electrical Properties of Polymers. 2nd Edition, Cambridge University Press, Cambridge.
- 23. Kwan, K. (2004) Dielectric Phenomena in Solids. Academic Press, New York.
NOTES
*Corresponding author.














