Open Journal of Applied Sciences
Vol.05 No.06(2015), Article ID:56696,7 pages
10.4236/ojapps.2015.56024
Quantum-Inspired Neural Networks with Application
Jianping Li
School of Computer and Information Technology, Northeast Petroleum University, Daqing, China
Email: leejp@126.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 May 2015; accepted 24 May 2015; published 27 May 2015
ABSTRACT
In this paper, a novel neural network is proposed based on quantum rotation gate and controlled- NOT gate. Both the input layer and the hide layer are quantum-inspired neurons. The input is given by qubits, and the output is the probability of qubit in the state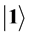 . By employing the gradient descent method, a training algorithm is introduced. The experimental results show that this model is superior to the common BP networks.
. By employing the gradient descent method, a training algorithm is introduced. The experimental results show that this model is superior to the common BP networks.
Keywords:
Quantum Computing, Neural Networks, Algorithm Design

1. Introduction
In the eighties of the twentieth century, Benioff and Feynman proposed the concept of quantum computation, and then P.W. Shor gave the first quantum algorithm of very large integer factorization [1] in 1994 and L.K. Grover proposed a quantum algorithm which searches a marked state in an unordered list [2] in 1996. Quantum computation has been widely paid attention and become a challenging research line. Fuzzy logic, evolution calculation, and neural networks are regarded as the most promising three important aspects in the artificial intelligence field, which compose intelligence calculation (soft calculation) and have much comparability with quantum computation. Therefore, the combination of them would bring promising research in theory.
Some research results in the nineties of the twentieth century show that [3] - [5] the information processing of brain may be related to the quantum states; there may exists the effect of quantum mechanics in brain, and the quantum system has the same dynamics features as the biology neural networks. Fatt and Katz proved that in biology neuron, the neurotransmitter is released from the nerve terminals by the form of multi-molecule and small units, and they call this kind of small units quantum. Each of small units (quantum) describes the minimal unit that the neurotransmitter is released. In general, although the number of quantum in each synaptic response of neurons may be different, the number of molecules in each quantum is the same. Therefore, the combination of quantum computation and ANN may preferably simulate the information processing of brain.
However, as yet, there is little understanding of the essential components of artificial neural networks based on quantum theoretical concepts and techniques. The basal model and theory of quantum neural networks are in research. At present, there is not a set of perfect theory to direct the construction of model. Since Kak firstly proposed the concept of quantum neural computation [6] in 1995, the quantum neural networks have been paid attention, and many novel ideas and elementary model have been proposed. In 1997, N. B. Karayiannis et al. proposed the model of quantum neural networks with multilevel hidden neurons based on the superposition of quantum states in quantum theory. ZHU Da-qi et al. applied this model to fault diagnosis for photovoltaic radar electronic equipment, and acquired the satisfied results [7] . In 2000, Matsui et al. proposed a quantum neural networks model based on the single bit rotation gate and the 2-bit controlled-NOT gate, presented the algorithm of model, and investigated its performance on solving the 4-bit parity check problem and the function approximation problem [8] . In this model, the input is based on quantum bits (qubits). However, in many actual problems, the system input is the real vector in Hilbert space, and the method is not presented to transform the real to the quantum state in Ref. [8] . For the algorithm of model, the only two iterative equations in complex number are given based on the gradient descent algorithm. Neither the gradient computation formula nor the input-output relationship of networks is presented. Therefore, it is not easy for the reader to simulate the algorithm and apply this model to actual problem.
In this paper, based on the universality of the single qubit rotation gate and the two-qubit controlled-NOT gate, a quantum neuron model and three layers quantum back-propagation neural networks (QBP) model are proposed. The learning algorithm in Ref. [8] is improved. A transform method from the real to the qubit is proposed. On the basis of the probability amplitude vector of qubits, the input-output relationship of the model is presented. To facilitate the practical application, the learning algorithm is deducted in detail and the implementing scheme is given. The continuity of this model is theoretically proved. Two application examples are designed, and the simulation results show that this model and algorithm are evidently superior to the conventional back-propaga- tion networks (CBP) in three aspects: convergence speed, convergence rate, and robustness.
2. The Qubit and Quantum Gates
2.1. The Qubit
In the quantum computation, the term “qubit” is introduced as the counterpart of the “bit” in the conventional computation to describe the state of quantum computation. In quantum computation system two quantum physical states labeled as 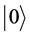 and
and 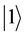 express 1 bit information.
express 1 bit information. 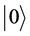 corresponds to the bit 0 of classical computation, while the
corresponds to the bit 0 of classical computation, while the 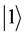 to the bit 1. The qubit state
to the bit 1. The qubit state 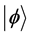 maintains a coherent superposition of states
maintains a coherent superposition of states 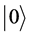 and
and 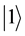
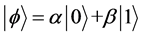 (1)
(1)
where 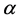 and
and 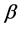 are complex numbers called probability amplitude. That is, the qubit state
are complex numbers called probability amplitude. That is, the qubit state 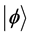 collapses into either
collapses into either 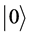 state with probability
state with probability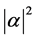 , or
, or 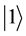 state with probability
state with probability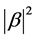 , and
, and

Therefore, the qubit can also be described by the probability amplitudes as
2.2. The Quantum Gate
The definition of single qubit rotation gate is described as follows

Let the quantum state




The effect of the quantum NOT gate is exchange the two probability amplitudes of a qubit, and its definition is described as follows

Using the method proposed in Ref. [8] , the controlled-NON gate can be realized by Equation (5)

According to the different value of the controlled parameter
(1) If

(2) If

bability amplitude of quantum state 
(3) If

3. The Quantum-Inspired Neural Networks Model
3.1. The Quantum-Inspired Neuron
On the basis of the universal quantum gates, the quantum neuron model proposed in this paper includes five parts: input, phase rotation, aggregation, reverse rotation and output, where the input is described by qubits, the output is given by the probability of the state in which 


Where the definition of 


where f is a sigmoid function, and the definition of 


Figure 1.The quantum-inspired neuron model.
follows

The result of reverse rotation is given by

The input-output relationship of quantum neuron is described as follows

3.2. The Quantum-Inspired Neural Networks
The quantum neural networks are composed of some quantum neurons and conventional neurons according to the definite linking rule. The three layers feed-forward QBP model proposed in this paper is shown in Figure 2, where the input layer and the hidden layer has n, p quantum neurons, respectively, and the output layer has m conventional neurons.
Suppose 








where


4. Training Algorithm
For the training samples described in the n-dimension Euclid-space

where
Figure 2. Three layers quantum-inspired networks model.
In the QBP described by Figure 2, there are three groups of parameters, the rotation parameter



where 

Let


Let





The parameter updating rules are as follows



where 
5. Simulation Comparisons
To testify the validity of QBP, an actual example is designed and the QBP is compared with the CBP in this section. To make comparison equitable, the QBP adopts the same structure and parameters as CBP in the simulations.
The XOR problem has been the typical example of the neural networks learning algorithm research. This problem is the simplest example for nonlinear classification problem, which the corresponding optimization surface is irregular, and exists some local minimum. In this simulation, The XOR problem is generalized from four points to sixteen points. The point set is shown in Figure 3.
Firstly, we investigate how to change for the convergence rate when the learning coefficient changes. The networks structure is set to 2-10-1, the restriction error is 0.1, and the restriction iteration steps are 2000. The learning coefficient is from {0.1, 0.2, ・・・, 1.0}. This example is simulated 100 times for each learning coefficient by the QBP and the CBP, respectively. When the learning coefficient changes, the maximum of convergence rate of QBP is 87% and the minimum is 51%. However, the convergence rate of CBP changes in a large range when the learning coefficient changes. When the learning coefficient is less than 0.2, the convergence rate of CBP is 0%, and when the learning coefficient is more than 0.2, the maximum of convergence rate of CBP is
Figure 3. Sixteen points distribution on the plane.
Figure 4. The relation of the convergence rate and
Figure 5. The relation of the iteration steps and
Figure 6. The relation between the iteration steps and the restriction error.
only 59%. The comparison result is shown in Figure 4.
The comparison result shows that the QBP is evidently superior to the CBP in both the convergence rate and the robustness.
Secondly, we investigate how to change for the iteration steps when the learning coefficient changes. The networks structure is set to
The comparison result shows that the QBP is evidently superior to the CBP in both the iteration steps and its fluctuation range when the learning coefficient changes.
Finally, we investigate how to change for the iteration steps when the restriction error changes. The networks structure is set to
When the restriction error changes, for the average iteration steps of QBP, the maximum is 8575 steps, and the minimum is 431 steps; for the minimum iteration steps of QBP, the maximum is 1816 steps, and the minimum is 30 steps. However, for the average iteration steps of CBP, the maximum is 17,100 steps, and the minimum is 1304 steps; for the minimum iteration steps of CBP, the maximum is 14,525 steps, and the minimum is 659 steps. Hence, when the restriction error changes, the iteration steps and its fluctuation range of QBP is far less than that of CBP, which takes on the preferable robustness.
6. Conclusion
On the basis of the qubits and the universal quantum gates, a quantum BP neural networks model is proposed; the learning algorithm of this model is designed; and the continuity of this model is proved. The simulation result shows that this model and algorithm are superior to conventional BP networks in three aspects: the convergence speed, convergence rate, and robustness, by an actual example of pattern recognition and function approximation.
Cite this paper
Jianping Li, (2015) Quantum-Inspired Neural Networks with Application. Open Journal of Applied Sciences,05,233-239. doi: 10.4236/ojapps.2015.56024
References
- 1. Shor, P.W. (1994) Algorithms for Quantum Computation: Discrete Logarithms and Factoring. 35th Annual Symposium on Foundations of Computer Science, New Mexico, 20-22 November 1994, 124-134. http://dx.doi.org/10.1109/SFCS.1994.365700
- 2. Grover, L.K. (1996) A Fast Quantum Mechanical Algorithm for Database Search. Proceedings of the 28th Annual ACM Symposium on the Theory of Computing, Pennsylvania, 212-221.
http://dx.doi.org/10.1145/237814.237866 - 3. Perus, M. (1996) Neuro-Quantum Parallelism in Brain-Mind and Computers. Informatics, 20, 173-183.
- 4. Adenilton, J., Wilson, R. and Teresa, B. (2012) Classical and Superposed Learning for Quantum Weightless Neural Network. Neurocomputing, 75, 52-60.
http://dx.doi.org/10.1016/j.neucom.2011.03.055 - 5. Israel, G.C., Angel, G.C. and Belen, R.M. (2011) Dealing with Limited Data in Ballistic Impact Scenarios: An Empirical Comparison of Different Neural Network Approaches. Application Intelligence, 35, 89-109. http://dx.doi.org/10.1007/s10489-009-0205-8
- 6. Kak, S. (1995) On Quantum Neural Computing. Information Sciences, 19, 143-160.
http://dx.doi.org/10.1016/0020-0255(94)00095-S - 7. Zhu, D.Q. and Sang, Q.B. (2006) A Fault Diagnosis Algorithm for the Photovoltaic Radar Electronic Equipment Based on Quantum Neural Networks. Acta Electronica Sinica, 34, 573-576.
- 8. Matsui, N., Kouda, N. and Nishimura, H. (2000) Neural Networks Based on QBP and Its Performance. Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, 3, 247-252.
http://dx.doi.org/10.1109/ijcnn.2000.861311







