Open Journal of Applied Sciences
Vol.05 No.02(2015), Article ID:53717,6 pages
10.4236/ojapps.2015.52004
Explanation of Capacitive Performance of the Plasma in Damavand Tokamak
Shervin Goudarzi1, Fatemeh Dadgarnejad2, Hojat Babaee1
1Atomic Energy Organization of Iran, Nuclear Science and Technology Research Center, Plasma Physics and Nuclear Fusion Research School, Tehran, Iran
2Nuclear Science & Technology Research Institute, Atomic Energy Organization of Iran, Tehran, Iran
Email: sgoudarzi@aeoi.org.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 December 2014; accepted 15 January 2015; published 2 February 2015
ABSTRACT
In this work capacity of tokamak plasma is calculated using modeling of tokamak configuration as toroidal and coaxial capacitor. This value is very important and plays an important role in time- varying regimes in tokamak. For exact simulation of plasma behavior, this amount will be added to circuit equations and transport codes. Since capacitive properties of tokamak cause production of a radial electric field, it deserves our special attention.
Keywords:
Tokamak, Capacitive Properties, Radial Electric Field

1. Introduction
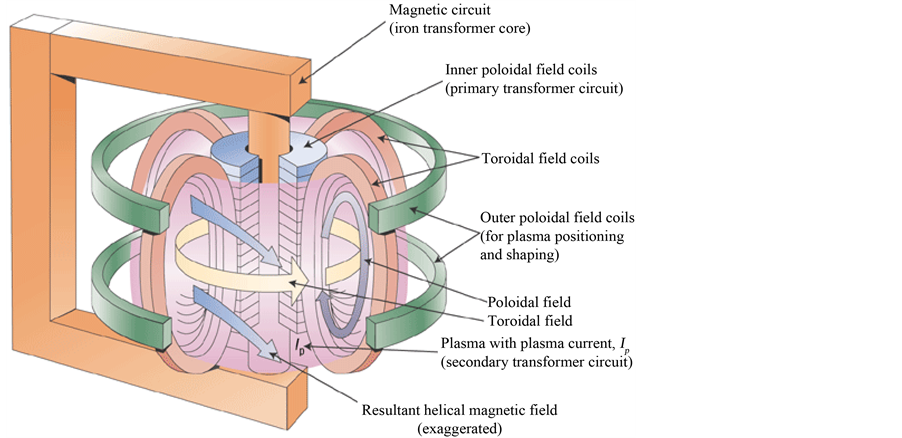
Tokamak is a torodial shape magnetic confinement fusion device that is the best candidate for nuclear fusion reactors [1] [2] . Working principle of this device is like a transformer, passing the electric current through the primary coils inducing a current in the tokamak plasma that plays the role of secondary coils of transformer (Figure 1) [1] -[3] . This current causes heating of the plasma and creates a polar magnetic field Bθ which increases the quality of the confinement of tokamak plasmas. The resistive and inductive properties of the plasma in tokamak have been widely studied. Though the plasma has capacitance property in all area between its centre and the chamber wall, its capacitive performance was not widely studied before 1990’s [4] [5] . In this article, the capacitive property of the plasma in the tokamak and its importance in circuit equations and transport codes of tokamak is explained. Then, the numerical results of such model for Damavand tokamak compare with experimental results and a good agreement between them is observed.
2. The Capacitive Model
Estimation the value of capacitance of the equal circuit of tokamak can be done by a torodial coaxial capacitor (Figure 2), the tokamak plasma plays the role of inner electrode and the discharge chamber wall is external electrode and the low-density plasma between them considered as the dielectric of capacitor. In this article, the capacity of tokamak plasma obtained through solving the Laplace equation for a torus, and the working regimes in which this property is important have been identified.
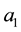 ,
,
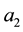 and
and
 are the distance between centre of plasma and its edge, tokamak minor radius and major radius of the tokamak, respectively. Here the main problem is the solving of the Laplace equation for
are the distance between centre of plasma and its edge, tokamak minor radius and major radius of the tokamak, respectively. Here the main problem is the solving of the Laplace equation for
 with the boundary conditions of (
with the boundary conditions of ( in
in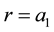 ) and (
) and (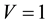 in
in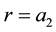 ).
).
The Laplace equation [6] :
 (1)
(1)
 ,
, and
and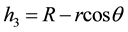
With substituting the above values in Equation (1) and with respect to that in this system
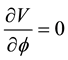 the Equa-
the Equa-
tion (1) becomes as follows.
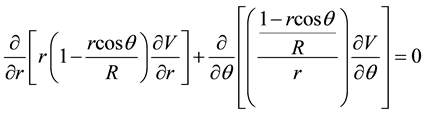 (2)
(2)
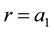 :
: 
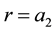 :
:
Because of the uniqueness of the solutions of Laplace equation, there will be only one answer that will satisfy the above conditions.
It is obvious that in a constant , the solution of Equation (2)
, the solution of Equation (2)


period is



scribed as a cosine Fourier series of



Figure 2. Coaxial torus [2] .

Now, it is necessary to obtain expressions for

the simplest solution, we first put the


the coefficients of

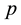



On the other hand, the solution to Laplace equation for such coordinate system would be in the form of
This solution provides the boundary conditions



With respect to that the boundaries are considered as co-potential surface, on them
electrical charge on each surface of torus is equal to

In this relation




By putting the calculated values for






Since



In limit of



the same formula for capacitance in concentric cylinders. It should be noted that

as






magnetic field, mass density and velocity of light, respectively. Because the values of



The electrical equivalent circuit for tokamak after taking into account the capacitor property is shown in Figure 3 in which



calculated by


equations,





In Equation (8),


The general solution of Equation (9) for the plasma current can be written as:

Figure 3. RLC equivalent circuit of tokamak plasmas.
In Equation (10)


damping constant, respectively.

rent, respectively.



important factor that can play an important role in various regimes of the tokamak plasma. The values of natural frequencies for different tokamaks are in order of
In fact, according to the properties of electrical elements, in dc regimes (following the end of transient regimes),




The first effects of capacitance are weak damping oscillations with natural frequency in plasma current, radial electric fields and so on, detection of them is usually difficult. Its second effects are to cause some types of fluctuations in density and other plasma parameters at the edge of plasma. Such fluctuations have been observed in Damavand tokamak [4] . Probably, some fluctuations in kHz range in H mode of tokamak and in plasma edge can be related to the natural frequency discussed above. When the value of

3. Results and Discussion
The experimental data of the Damavand tokamak are [10] :








On the basis of dimension and condition of Damavand tokamak we would have:




After some calculating it would be:
And, therefore, it would be:


As previously noted, the first effect of the capacitance is weak damping oscillations with the frequency



In the experiments with Damavand tokamak that a sample of their results is demonstrated in Figure 4, when
the negative spike of loop voltage is observed, the disruption instability happened and

damping oscillations. From the calculations using the presented model, it is seen that the frequency of these oscillations is approximately 100 kHz with damping in form of
them is observed [10] .

When a power source (such as induced current, radio frequency wave, neutral beam) is injected into the plasma, there will be two working regimes:
1) The first one is a transient regime in which L and C along with R play role in equation of circuit and to simulate the behaviour of the plasma, using RLC circuit (Figure 3) with Equation (9) is necessary.
2) In the second regime that is a steady state regime, a simple resistive circuit with circuit equation of

Therefore, the capacitance of the plasma like its inductance, plays important role in some working regimes of tokamak. The importance of capacitance properties is not limited to regimes with time-varying loop voltages. In
each transient regime and regimes with time varying power source (such as radio frequency waves and neutral beam heating) the effect of capacitive property can be seen. In Figure 3, in addition to an electrical power supply, radio frequency waves and neutral beams can be considered as the power supply.
4. Conclusions
The radial electric field in study of the H mode of tokamak plasmas is a very important parameter and several models have been proposed to explain the origin of them. In this paper, the effects of capacitive property on radial electric field in tokamak are briefly explained. It is proposed that a radial electric field is produced by a ra-
dial current in the form of


Then, a new model for equivalent circuit of tokamak plasmas on the base of capacitive property is explained. The plasma has the capacitive property of


in the form of
value for capacitance in Equation (8) and Figure 3 which gives more accurate results.
In this article, the analysis on the base of this model is first accomplished for Damavand tokamak and a good agreement between results of this model and the experimental results is observed. This model may be extended in future for analysis of the performance of big tokamaks such as ITER.
References
- Friedberg, J. (2007) Plasma Physics and Fusion Energy. 1st Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511755705
- Wesson, J. (1987) Tokamaks. 1st Edition, Oxford Science Publication, Oxford.
- Loarte, A. (2006) Chaos Cuts ELMs down to Size. Nature Physics, 2, 369-370. http://dx.doi.org/10.1038/nphys331
- Amrollahi, R. and Farshi, E. (1996) Modelling an RLC Circuit for the Investigation of the Disruption Instabilities in Tokamaks. Proceedings of the 16th IAEA Fusion Energy Conference, Montreal, 7-11 October 1996, 649-654.
- Itoh, K., Itoh, S.I. and Fukuyama, A. (1999) Transport and Structural Formation in Plasmas. 1st Edition, IOP Publishing, Bristol.
- Jackson, J.D. (1998) Classical Electrodynamics. 3rd Edition, John Wiley & Sons, New York.
- Inan, U.S. and Gokowski, M. (2011) Principles of Plasma Physics for Engineers and Scientists. Cambridge University Press, Cambridge.
- Spitzer, L. and Harm, R. (1953) Transport Phenomena in a Completely Ionized Gas. Physical Review, 89, 977. http://dx.doi.org/10.1103/PhysRev.89.977
- Fish, N.J. (1985) Conductivity of RF-Heated Plasma. Physics of Fluids, 28, 245-247. http://dx.doi.org/10.1063/1.865186
- Farshi, E., Brevnov, N., Bortnikov, A., Gott, Y. and Shurygin, V. (2001) Some Characteristics of the Predisruption Phase in Tokamaks. Physic of Plasmas, 8, 3587-3594. http://dx.doi.org/10.1063/1.1379969






