Received 9 June 2014; revised 22 July 2014; accepted 2 August 2014

ABSTRACT

Let 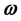be a Muckenhoupt weight. In this paper we get the estimate of rearrangement 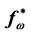in homogeneous space that is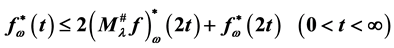. The similar estimate is obtained only on space of.

Keywords:

Rearrangement, Homogeneous Space, Weight

1. Introduction

We first recall some basic notions about the homogeneous space and the weights we are going to use.

Definition 1 [1] . (Homogeneous space X). Let X be a set. A function d: 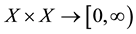is called a quasi- distance on X if the following conditions are satisfied:

1) for every x and y in X, 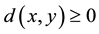, and 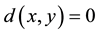if and only if x = y,

2) for every x and y in X, ,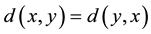

3) there exists a constant K such that for every x, y and z in X.

Let μ be a positive measure on the 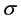-algebra of subsets of X generated by the d-balls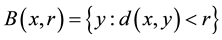, with 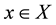and r > 0. Then a structure (X, d, μ), with d and μ as above, is called a space of homogeneous type.

We say that (X, d, μ) is a space of homogeneous type regular in measure if μ is regular, that is for every measurable set E, given, there exists an open set G such that and. In what follows we always assume that the space (X, d, μ) is regular in measure.

A non-negative locally integrable on homogeneous space X function is called a weight. With any

weight function we call the measure. Given a measurable function f on homogeneous space

X, define its non-increasing rearrangement with respect to a weight similar to (see [1] , p. 32).

(1)

Definition 2 (weight) [2] . A weight is in Muckenhoupt’s class respect to μ if there are positive constants C and such that the inequality:

holds for every ball B and every measurable set. The infimum of such C will be denoted by.

2. Basic Lemmas

Denote doubling condition D, a weight if and only if for any ball holds. Clearly if then.

Lemma 1 [3] . Let (X, d, μ) be a space of homogeneous type. Let be a family of balls in X such that is measurable and. Then there exists a disjoint sequence, possibly finite, such that for some constant C. Moreover, every is contained in

some.

Lemma 2. (C-Z decomposition) [4] [5] . Let (X, d, μ) be a space of homogeneous type such that the open balls are open sets. Let f be a nonnegative integrable function defined on X, then for every (if), there exist a sequence of disjoint balls such that if, C is the constant in Lemma [1] then

1),

2) for every ball B centered at, holds.

Lemma 3. and, If X is a ball and is an arbitrary measurable set of positive measure with , there exist mutually disjoint balls such that

B_i cover E and

Proof: If

Letting, then

then

For every ball B centered at

i.e.

,

If there exist and, now exists such that, then

,

this is a contradiction.

Then and

.

3. Inequalities Conclusion

Theorem 1. then .

Proof: The proof is similar to Lerner [5] - [7] ,

From [6] , We get two collections of balls, then

Fix X, with, for all E, there is, then exist dis-

joint balls, hold

Which contains

Then

Select from the balls, which are not contained in,

. That is for all. There exist then

Note that

Since

Then

,

i.e.

.

We have

Taking supremum over all with, we get the argument .

Fund

A project supported by scientific research fund of Hunan provincial education department in China (NO: 13C 955).

References