Open Journal of Applied Sciences
Vol.04 No.10(2014), Article ID:49489,3 pages
10.4236/ojapps.2014.410048
Analytical Solution of Kolmogorov Equations for Four-Condition Homogenous, Symmetric and Ergodic System
Victor V. Kravets1, Konstantin M. Bass1, Vladimir V. Kravets1, Larisa A. Tokar2
1Department of Automobiles and Automobile Sector, National Mining University, Dnepropetrovsk, Ukraine
2Foreign Languages Department National, Mining University, Dnepropetrovsk, Ukraine
Email: prof.w.kravets@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 July 2014; revised 22 August 2014; accepted 4 September 2014
ABSTRACT
Technical system consisting of two independent subsystems (e.g. hybrid car) is considered. Graduated state graph being homogenous ergodic system of symmetric structure is constructed for the system. Differential Kolmogorov equations, describing homogenous Markovian processes with discrete states and continuous time, are listed in symmetric matrix form. Properties of symmetry of matrix of subsystem failure and recovery flow intensity are analyzed. Dependences of characteristic equation coefficients on intensity of failure and recovery flows are obtained. It is demonstrated that the coefficients of characteristic equation meet the demands of functional dependence matching proposed visible analytical solution of complete algebraic equation of fourth order. Depending upon intensity of failure and recovery flows, four roots of characteristic equation are analytically found out. Analytical formulae for state probability of interactive technical system depending upon the roots of characteristic equation are determined using structurally ordered symmetric determinants, involving proper column of set initial data as well as subsystem failure and recovery flow intensity are proposed.
Keywords:
state graph, Markovian process, Kolmogorov equations, intensity matrix, characteristic equations, state probabilities

1. Introduction
Studies of homogenous Markovian processes with discrete states and continuous time in ergodic systems result in generating and solving Kolmogorov equations [1] . Kolmogorov equations are homogenous system of ordinary linear differential equations with constant coefficients; their analytical solution amounts to determining roots of characteristic degree equation equal to system order of differential equations [2] . Analytical solutions of characteristic equations (complete algebraic equations) are limited by fourth order (Cardano formulae and Ferrari formulae); however, they are slightly used due to their awkwardness. It is of practical interest applying specific analytical solution for complete algebraic equations reflecting qualitatively harmonic root distribution within complex plane [3] . The paper illustrates the use of such a specific analytical solution [4] for biquadratic ergodic system which state graph is of symmetrical structure. A new compact record of analytical solution for Kolmogorov equation involved simply ordered determinant contrary to classic solving systems of differential equations resulting in immense, awkward structureless record of desirable formulae. Determined formulae of random state of interactive technical system make opportunity of deep analysis of random processes with the help of analytical methods, and numerical ones having applied computer.
2. Setting up a Problem
Markovian processes with discrete states and continuous time within technical system are considered; its state graph is of following symmetrical type (Figure 1):
Where Si(i = 1, 2, 3, 4) are states of technical system (TS) involving two independent subsystems. The subsystems are in two conditions: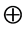 —operational condition, and
—operational condition, and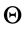 —inoperable one.
—inoperable one.
Intensity of failure flows (λ1, λ2) and recovery flows (µ1, µ2) of the two subsystems is set as given and constant. It is required to determine state probability of interactive technical system Pi (t) (I = 1, 2, 3, 4) under certain condition of the system in start time Pi (0).
3. Kolmogorov Equations
Kolmogorov equations are set up in accordance with set state graph taking following symmetrical matrix form:
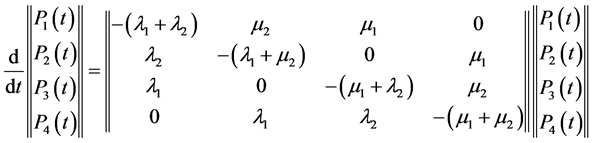
where the matrix of failures and recoveries is ordered, i.e. when it is asymmetrical to the main diagonal and symmetrical to secondary diagonal, then it has central asymmetry. Subsequently, coefficients of characteristic equations are:
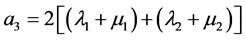 ;
;
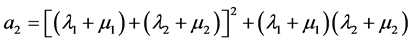 ;
;
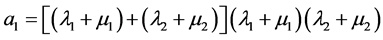 ;
;
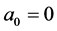
meeting the requirement:
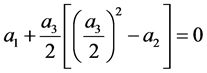 ,
,
Analytically, roots of characteristic equation are found out by [3] [4] formula:
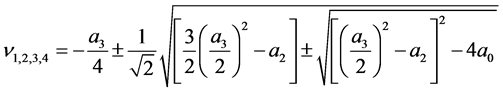 ,
,
that is
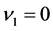 ,
,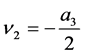 ,
,
Figure 1. State graph of a technical system.
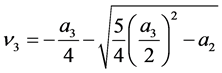 ,
,
Respectively, expressing roots of characteristic equation in terms of intensity of failures and recoveries of the two subsystems, we obtain:

4. Analytical Solution
Symbolize analytical solution of initial matrix fourth-order Kolmogorov equation in a normalized form based on structurally simple determinants:

where
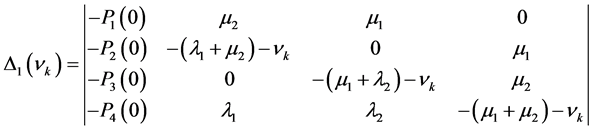 etc.
etc.
For example, it is supposed that: .
.
5. Conclusion
Fourth-order Kolmogorov equations for state probabilities of TS consisting of two subsystems are represented in a symmetrical matrix form. The form is reflected in ordered symmetrical record of characteristic determinant. The characteristic determinant ordering is expressed in structurally simple formulae for coefficients of dependence-bonded characteristic equation. The dependence demonstrates the nature of symmetry under consideration. Functional dependence of characteristic equation coefficients motivates qualitatively harmonic distribution of roots within complex plane in the form of central symmetry. Specified property of the symmetry makes it possible to apply visible formula to calculate roots of characteristic equation of fourth order. Analytical solution for Kolmogorov equation is represented in the form of structurally simple and ordered determinants to analyze interactive state probability of TS.
References
- Venttsel, E.S. and Ovcharov L.A. (1991).Theory of Random Processes and Its Engineering Applications. Moscow, 384 p.
- Smirnov, V.I. (1974) A Course on Higher Mathematics. Moscow, Vol. 2, 656p.
- Kravets, V. and Chibushov, Y (1994) Method of Finding the Analytical Solution of the Algebraic Particular Aspect Equation, Poland, Rzeszow, Folia Sci. Univ. Tech. Resoviensis, Math. 16, 104-117.
- Kravets, V.V. (1972) On the Solving Certain Engineering Problems, Amounting to Find Roots of Particular-Type Algebraic Equation, Selected works “Best Practices of Electrification of Mining-and-Processing Integrated Works in Dnepropetrovsk Region”, Dnepropetrovsk, 107-109 pp.


