Open Journal of Applied Sciences
Vol.04 No.08(2014), Article ID:47734,7 pages
10.4236/ojapps.2014.48039
Effects of Differential Item Discriminations between Individual-Level and Cluster-Level under the Multilevel Item Response Theory Model
Chalie Patarapichayatham, Akihito Kamata
Southern Methodist University, University Park, USA
Email: cpatarapichy@smu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 May 2014; revised 17 June 2014; accepted 29 June 2014
ABSTRACT
This study attempted to interpret differential item discriminations between individual and cluster levels by focusing on patterns and magnitudes of item discriminations under 2PL multilevel IRT model through a set of variety simulation conditions. The consistency between the mean of indi- vidual-level ability estimates and cluster-level ability estimates was evaluated by the correlations between them. As a result, it was found that they were highly correlated if the patterns of item discriminations were the same for both individual and cluster levels. The magnitudes of item dis- criminations themselves did not affect much on correlations, as far as the patterns were the same at the two levels. However, it was found that the correlation became lower when the patterns of item discriminations were different between the individual and cluster levels. Also, it was re- vealed that the mean of the estimated individual-level abilities would not be necessarily a good representation of the cluster-level ability, if the patterns were different at the two levels.
Keywords:
Multilevel Item Response Theory Model, Ability Estimates, Item Discrimination

1. Introduction
Multilevel modeling has become a popular data analysis technique in psychological and educational measure- ment. Traditional psychometric models, such as classical test theory and item response theory (IRT) models, do not account for a nested structure of the data. Multilevel modeling becomes important when researchers analyze nested data, because it takes into account of both within and between cluster variations of the data. One of pop- ular multilevel modeling techniques is a hierarchical generalized linear model (HGLM). However, when HGLM is applied to multilevel IRT [1] , one limitation is that all item discriminations are assumed to be equal. In other words, the relationships between the observed measurement indicators and the latent factor are assumed to be equal for all items in a test, which is sometimes an unrealistic assumption. If item discriminations are allowed to freely vary, the model may more closely resemble the observed data.
IRT models define the relationship between observed item scores and latent constructs for dichotomous and polytomous item response data. An IRT framework has been extended to a multilevel data structure [1] - [3] . A multilevel IRT model is desirable when item response data have been collected from a sample with a nested data structure. In addition to the benefit of modeling data variations both at between and within cluster levels, rela- tionships between variables at different levels can be estimated better as well.
One popular form of an IRT model for dichotomously scored items is a 2-parameter logistic (2PL) model, where the probability of an individual correctly responding to an item depends on individual’s ability, item dif- ficulty, and item discrimination. The 2PL IRT model can be written as
 , (1)
, (1)
where
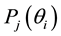 is the probability that individual i with ability
is the probability that individual i with ability
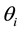 answers item j correctly,
answers item j correctly,
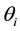 is an ability lev- el for individual i,
is an ability lev- el for individual i,
 is an item discrimination parameter for item j, and
is an item discrimination parameter for item j, and
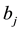 is an item difficulty parameter for item j. The numerator and the second term in the denominator
is an item difficulty parameter for item j. The numerator and the second term in the denominator
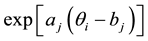 correspond to the odds ra- tio of a correct response
correspond to the odds ra- tio of a correct response .
.
The 2PL IRT model also allows the item discriminations to vary freely across items in a test. Its extension to a multilevel IRT model has been investigated and documented by several authors [4] - [9] . However, not much at- tention has been given to what it means when patterns and/or magnitudes of item discriminations are different between individual and cluster levels. For example, Fox [4] illustrated the importance of taking measurement errors from different sources into account by a multilevel analysis. Although the author presented a new ap- proach to multilevel modeling with three real data sets of mathematics by using 2PL IRT model, difference in item discriminations between levels were beyond his focus. Fox [5] focused on measuring latent dependent and independent variables of a multilevel model, where manifest variables consisting of binary, ordinal, or graded responses. This extension made it possible to model relationships between observed and latent variables on dif- ferent levels using dichotomous and polytomous IRT models. However, different item discrimination patterns between levels were not a focus of this study. Natesan [7] studied the accuracy and precision of the item para- meter estimates of the 2PL multilevel IRT model by varying test lengths, sample sizes, correlation between the predictor variable and the ability parameter, and the distribution shape of the predictor variables interact to im- pact the accuracy and the precision. Again, differential item discrimination patters between levels were not a fo- cus of this study.
Some authors investigated a cluster-level IRT modeling. For example, Mislevy [6] proposed a notion of the cluster-level IRT model by exploring the relationships between individual-level and cluster-level IRT models, as well as the parameter estimates under the cluster-level IRT model. Results showed that when item response data are gathered in a design of one item per scale from each individual, it is possible to define a cluster-level IRT model. The cluster-level ability estimate was analogous to the individual-level ability estimates. The cluster- level IRT model parameters specified the probability of a correct response to a given item from an individual selected at random from a given cluster. The cluster-level IRT model parameter estimate was a straightforward generalization of an individual-level IRT model technique. Tate [8] studied whether the cluster-level IRT model was robust to typical violations of distributional assumptions under the two-parameter cluster-level IRT dicho- tomous model through a simulation study. Results showed that the estimated precision was always either ap- proximately consistent with the actual precision or a conservative estimate of the actual precision. When the items were replaced to target high-ability schools, the conservatism increased as school ability moved away from the target ability range. Also, Tate [9] extended to a similar study with a polytomous model. Results were similar to findings from [8] . It is notable that Tate [9] concluded that the estimate of cluster-level ability for a specific cluster could be viewed as the mean of the individual-level ability of all individuals in that cluster if the individual abilities within each cluster are normally distributed with a mean equal to the cluster-level ability, and the cluster-level ability is also normally distributed. However, no discussion was provided regarding the effect of differential item discriminations between individual and cluster levels. Our concern was whether the patterns and the magnitudes of the item discrimination between levels would affect the estimates of individual or cluster level abilities differently.
Assuming we fit a 1PL multilevel IRT model. The pattern of item discrimination would be exactly the same for both individual and cluster levels. In other word, it obtains only one pattern of the item discriminations for both levels (e.g., same pattern of item discrimination across both levels). The magnitudes of item discrimination would be exactly the same for both individual and cluster levels (e.g., 1.0 for all items across both levels). On the other hand, once the 2PL IRT model is applied to the multilevel model, the patterns and the magnitudes of the item discrimination could be different across levels. While the item discriminations may have the same pat- terns and the same magnitudes for both individual and cluster levels, the item discriminations may have the same patterns but different magnitudes between individual and cluster levels. The item discriminations may also have different patterns and different magnitudes between individual and cluster levels. However, effects of the difference in different patterns and magnitudes of item discrimination have not been demonstrated in literature yet with the multilevel IRT modeling perspective.
If differential patterns or magnitudes of item discriminations between levels affect estimates of individual and cluster level abilities differently, the conclusion that Tate [9] has made may not be always correct. Namely, esti- mated cluster-level ability should not always be viewed as the mean of the individual-level abilities in the cluster. Therefore, the mean individual level abilities may practically over- or under-estimates the cluster-level ability. In practice, it is not uncommon to estimate the cluster-level ability from the mean of the individual-level ability of all individuals in that cluster. For example, it is very common to evaluate school level performance by compu- ting the mean of estimated student abilities in each school. For these reason, we attempted to investigate how the patterns and the magnitudes of the item discrimination between individual and cluster levels would behave un- der the 2PL multilevel IRT model. It was also our intention to provide some insights on how we should interpret the differential item discriminations between individual and cluster levels.
An item discrimination indicates a quality of an item, because it dictates how strongly each item correlates with the ability being measured. A higher discrimination corresponds to a greater correlation with the ability, which also leads to a higher scoring weight for the item. Therefore, individuals who answer items with high dis- criminations correctly would have a higher estimated ability than individuals who answer items with lower dis- criminations correctly, given the same raw scores. In other words, it matters not only how many items were answered correctly, but also which items were answered correctly. Under the 2PL single-level IRT model, the individual ability estimates are weighted by item discriminations, such that
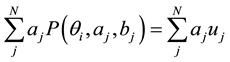 , (2)
, (2)
where
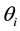 is an ability level for individual i,
is an ability level for individual i,
 is an item discrimination parameter for item j,
is an item discrimination parameter for item j,
 is an item difficulty parameter for item j, and
is an item difficulty parameter for item j, and
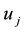 takes the values 0 and 1 corresponding to incorrect and correct res- ponses of individual i on item j (j = 1, 2, …, N). However, it may or may not be a case under the 2PL multilevel IRT model.
takes the values 0 and 1 corresponding to incorrect and correct res- ponses of individual i on item j (j = 1, 2, …, N). However, it may or may not be a case under the 2PL multilevel IRT model.
Since 2PL multilevel IRT model allows item discriminations to vary both at the individual and cluster levels, we hypothesized that different patterns of item discriminations between the levels affect patterns of scoring weights to be different between the levels. For this reason, our hypothesis was that the aggregated mean indi-
vidual-level abilities
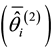 should be very close to the estimated cluster-level ability
should be very close to the estimated cluster-level ability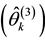 , if the patterns of
, if the patterns of
item discriminations are the same between the individual and cluster levels. However, if the patterns of item discriminations are different between the levels, we hypothesized that the aggregated mean individual-level abil-
ities
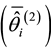 will be different from the estimated cluster-level ability
will be different from the estimated cluster-level ability



ter-level ability


mated cluster-level ability

2. Design of the Simulation Study
2.1. Modeling
The 2PL multilevel IRT model was investigated under this study for both data generation and fitting the model. In IRT, the response outcome data are treated as categorical with binomial distributions. The idea of a 2PL mul- tilevel IRT model is to measure each latent variable incorporated in the multilevel model with the IRT model. The 2PL multilevel IRT model can be written as

where








level k,


and



normal distribution with the mean of zero and the standard deviation of 1.0.
2.2. Simulation Conditions
It was assumed that the test consisted of 12 items with item difficulties ranging from −2.0 to 2.0. These item dif- ficulties were fixed across conditions. The biserial correlations between the ability estimate and the propensity for correct response were used to set up the item discriminations for individual and cluster levels. These five item discriminations (0.8, 1.0, 1.2, 1.6, and 2.2) represented biserial correlations of 0.40, 0.50, 0.55, 0.66, and 0.77 between the latent trait and the propensity to a correct answer. They created 16 sets of item discriminations classified into three patterns (see Table 1). The first pattern (Pattern A) was for conditions with the same pat- terns and the same magnitudes of discriminations for both levels. The second pattern (Pattern B) was for condi- tions with the same patterns but different magnitudes of discriminations between the levels, and the third pattern (Pattern C) was for conditions with different patterns and different magnitudes of discriminations between levels. Also, the number of clusters (2 levels; 50 and 100) and cluster size (2 levels; 50 and 100) were manipulated, and these three simulation factors were crossed and created a total of 16 × 2 × 2 = 64 simulation conditions.
Based on these specifications, the dichotomous item response data were randomly generated and fit by the 2PL multilevel IRT model as shown in Equation (3). The Mplus software, using the Maximum Likelihood esti- mator with robust standard errors was used to estimate model parameters (





ual-level abilities


evaluated the consistency of the aggregated mean individual-level abilities

level ability



3. Results and Discussions
Results demonstrated three primary scenarios regarding Pearson’s product moment correlation between the ag-
gregated mean individual-level abilities


Table 1. Item discriminations.
First, conditions with the same patterns and the same magnitudes of item discriminations for both levels (Pattern A), and conditions with the same patterns of item discriminations but the magnitude of item discriminations were higher for individual level (Sets 4, 7, and 8 under Pattern B), the correlations were very high. They were in the range of [0.757, 0.928]. These results indicated that the patterns and the magnitudes of item discriminations between levels affected the estimates and the correlations between the aggregated mean individual-level abilities


the mean of the individual-level ability of all individuals in that cluster. This statement also holds for the 1PL multilevel IRT as a special case. This result suggested that it is reasonable if one estimates the cluster-level abil- ity by computing the mean of the individual-level ability of all individuals in that cluster under these circums- tances. Both approaches would produce similar results. Also, within this pattern, the correlations slightly in- creased as the number of clusters and the cluster size increased.
Second, for conditions with the same patterns of item discriminations between levels but the magnitudes of item discriminations were lower for individual level (Sets 2, 3, and 6 under Pattern B), the correlations were moderately high. They were in the range of [0.497, 0.799]. These results showed that the individual level needed to be at least at the same level of item discriminations for cluster level for the aggregated mean individual-level
abilities


and the estimated cluster-level ability
some information when we aggregate the mean individual-level abilities
dividual-level abilities


Third, for conditions with different patterns and different magnitudes of item discriminations between levels (Pattern C), the correlations were much lower. They were in the range of [0.174, 0.462] among the six Pattern C
conditions. In this scenario, it became obvious that the aggregated mean individual-level abilities

the estimated cluster-level ability

item discriminations had a huge impact on the estimates of the aggregated mean individual-level abilities
and the estimated cluster-level ability
much on the estimates of the aggregated mean individual-level abilities

ability

generalization of the aggregated mean individual-level abilities
item discriminations under the 2PL multilevel IRT model behave differently from the differential item discrimi- nations under the 2PL single-level IRT model.
Overall, the Pearson’s product moment correlations between the aggregated mean individual-level abilities


and the estimated cluster-level ability




Note: C = number of cluster, CS = cluster size, A = conditions with the same patterns and the same magnitudes of item discriminations for both levels, B = conditions with the same patterns but different magnitudes of item discriminations between levels, C = conditions with different patterns and different magnitudes of item discriminations between levels, and 1, …, 16 = simulation sets 1 to 16.
Figure 1. Correlations between the aggregated mean individual-level abilities


the aggregated mean individual-level abilities


individual traits have different meaning than the cluster-level traits under conditions where the patterns and the magnitudes of the item discriminations differ.
Regarding the effect of simulation factors (see also Figure 1), for conditions with the same patterns and the same magnitudes of discriminations for both levels (Pattern A) and conditions with the same patterns but differ- ent magnitudes of discriminations between the levels (Pattern B), the correlations slightly increased as the num- ber of cluster and the cluster size increased. On the other hand, for conditions with different patterns and differ- ent magnitudes of discriminations between levels (Pattern C), the correlations slightly decreased as the number of cluster and the cluster size increased. These results demonstrated that the estimates of the aggregated mean
individual-level abilities


however, not necessarily in the way we typically understand the effect of sample size.
Regarding the effect of item discrimination magnitudes, first, for conditions with the same patterns and the same magnitudes of item discriminations for both levels (Pattern A), the correlations increased as the magni- tudes of either item discriminations for the individual level or item discriminations for the cluster level increased. These results were not surprising to us because the item discrimination indicates a quality of an item. A higher item discrimination corresponds to a greater correlation with the ability, which also leads to a higher scoring weight for the item.
Second, for conditions with the same patterns but different magnitudes of discriminations between the levels (Pattern B), the correlations increased as the magnitudes of item discriminations for the individual level in- creased, given the same magnitudes of item discriminations for the cluster level. On the other hand, the correla- tions decreased as the magnitudes of item discriminations for the cluster level increased, given the same magni- tudes of item discriminations for the individual level. Also, the correlations were much lower when the magni- tudes of item discriminations of the individual level were much lower than the magnitudes of item discrimina- tions of the cluster level. Thus, the difference in magnitudes of item discriminations between levels affected the
Estimates of the aggregated mean individual-level abilities


This result confirmed that the patterns of item discriminations have to be at least the same between levels to ob- tain similar estimates between the aggregated mean individual-level abilities




Third, for conditions with different patterns and different magnitudes of item discriminations between levels (Pattern C), the correlations decreased as the magnitudes of either item discriminations for the individual level or item discriminations for the cluster level increased. These findings were interesting, because they were dif- ferent from what we typically understand the effect of item discrimination; that is, higher item discrimination leads to a higher scoring weight for the item. If this statement is true under the 2PL multilevel IRT modeling, the aggregated mean individual-level abilities


ities


criminations and the magnitudes of either item discriminations for the individual level or item discriminations for the cluster level increased. This result also demonstrated that the patterns of the item discriminations had substantial effect on ability estimates under the 2PL multilevel IRT model.
Finally, it should be noted that there were interaction effects between our simulation factors. Namely, the cor-
relations between the aggregated mean individual-level abilities


4. Conclusions
Our investigation demonstrated one way to interpret differential item discriminations between individual and cluster levels in the 2PL multilevel IRT context. We found that the patterns of item discriminations between le- vels are more important than the magnitudes of item discriminations to obtain consistent estimates of the aggre-
gated mean individual-level abilities




vealed that this would be justifiable only if the magnitudes of item discriminations for both levels share the same patterns. For this reason, a caution should be made when aggregating individually estimated abilities, because
the mean of the estimated individual-level abilities


Although our investigation looked into three simulation factors over 64 simulation conditions, there are of course other factors and conditions that should be investigated. For example, it would be interesting to see how the number of items on each level would affect the estimates of the aggregated mean individual-level abilities


between levels. The item difficulty is another interesting factor. It would be interesting to see the effect of the interaction between the item difficulties and the patterns of item discriminations between levels. The extremely low or high item discrimination magnitudes under different patterns of item discriminations between levels should be of interest for future investigation. Also, it would be interesting to further algebraically demonstrate how the individual ability estimates are weighed by the differential item discriminations under the 2PL multile- vel IRT model.
References
- Kamata, A. (2001) Item Analysis by the Hierarchical Generalized Linear Model. Journal of Educational Measurement, 38, 79-93. http://dx.doi.org/10.1111/j.1745-3984.2001.tb01117.x
- Adams, R.J., Wilson, M. and Wu, M. (1997) Multilevel Item Response Models: An Approach to Errors in Variables Regression. Journal of Educational and Behavioral Statistics, 22, 47-76. http://dx.doi.org/10.3102/10769986022001047
- Fox, J.P. and Glas, C.A.W. (2001) Bayesian Estimation of a Multi-Level IRT Model Using Gibbs Sampling. Psycho- metrika, 66, 271-288. http://dx.doi.org/10.1007/BF02294839
- Fox, J.-P. (2004) Applications of Multilevel IRT Modeling. School Effectiveness and School Improvement, 15, 261- 280. http://dx.doi.org/10.1080/09243450512331383212
- Fox, J.-P. (2005) Multilevel IRT Using Dichotomous and Polytomous Response Data. British Journal of Mathematical and Statistical Psychology, 58, 145-172. http://dx.doi.org/10.1348/000711005X38951
- Mislevy, R.J. (1983) Item Response Models for Grouped Data. Journal of Educational Statistics, 8, 271-288. http://dx.doi.org/10.2307/1164913
- Natesan, P. (2007) Estimation of Two-Parameter Multilevel Item Response Models with Predictors: Simulation and Substantiation for an Urban School District. Unpublished Doctoral Dissertation, Texas A&M University, College Sta- tion, TX.
- Tate, R.L. (1995) Robustness of the School-Level IRT Model. Journal of Educational Measurement, 32, 145-162. http://dx.doi.org/10.1111/j.1745-3984.1995.tb00460.x
- Tate, R. (2000) Robustness of the School-Level Polytomous IRT Model. Educational and Psychological Measurement, 60, 20-37. http://dx.doi.org/10.1177/00131640021970349






