Open Journal of Applied Sciences
Vol.4 No.7(2014), Article
ID:46859,9
pages
DOI:10.4236/ojapps.2014.47036
Collective Behavior of a Ring of Van Der Pol Oscillators under Gaussian and Random Coupling Schemes
Miguel A. Barron, Dulce Y. Medina, Isaias Hilerio
Departamento de Materiales, Universidad Autonoma Metropolitana-Azcapotzalco, Mexico D.F., Mexico
Email: bmma@correo.azc.uam.mx, dyolotzin@correo.azc.ua.mx, ihc@correo.azc.uam.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2014; revised 23 May 2014; accepted 31 May 2014
ABSTRACT
The collective behavior of a ring of coupled identical van der Pol oscillators is numerically studied in this work. Constant, gaussian and random distributions of the coupling parameter along the ring are considered. Three values of the oscillators constant are assumed in order to cover from quasilinear to nonlinear dynamic performance. Single and multiple coupled frequencies are obtained using power spectra of the long term time series. Phase portraits are obtained from numerical simulations, and the coupled behavior is analyzed, compared and discussed.
Keywords:Coupled Oscillators, Coupling Parameter, Gaussian Distribution, Oscillators Ring, Random Distribution, Van Der Pol Oscillator

1. Introduction
It is known that the van der Pol oscillator can represent many oscillating systems in a wide variety of applications: biological rhythms [1] , heartbeat [2] [3] , chemical oscillations [4] , circadian rhythms [5] , and so on. The coupled behavior of van der Pol oscillators has been studied in the past considering different conditions and applying diverse analysis techniques, for example: diffusive displacement coupling [6] ; weak displacement coupling using harmonic balance [7] ; weak displacement and velocity couplings using perturbation methods [8] ; strong coupling with detuning using perturbation methods [9] ; strong diffusive coupling using matched asymptotic expansions [10] ; weak and moderate amplitude coupling with numerical solution [11] ; weak and strong bath coupling using Floquet theory and numerical solution [5] ; Whittaker method to determine the synchronized states in a ring of four mutually coupled non-identical van der Pol oscillators [12] .
Some works on the collective behavior of large rings of coupled van der Pol oscillators have been reported. In [13] the authors consider the synchronized states in a ring of mutually coupled self-sustained electrical oscillators described by coupled Van der Pol equations. They analyze the stability of the synchronization of the ring using the Floquet theory, the Whittaker method and numerical investigations. In [14] the dynamic behavior and synchronization of a very large ring of coupled van der Pol oscillators is studied by linearization and subsequent conversion of the original equations into a canonical Hill’s equation; the influence of the coupling parameter value on the ring stability is investigated by determining the value and sign of the non-periodic term of the Hill's equation. In a recent work [15] one of the present authors consider a ring of van der Pol oscillators, and the focus of his work is on the emergent behavior of a large number of oscillators. He determines the conditions under which time-independent solutions are obtained, and the linear stability of these solutions is investigated. Besides, the effect of the singularity of the coupling matrix on the ring dynamics is explored: when this becomes singular, an infinite number of steady states are present, and the phenomenon of oscillation death arises.
In [13] -[15] , the value of the coupling parameter remains constant along the ring. No variations or variable distributions of the coupling parameter along the ring are studied or even considered. In this work a ring of N identical van der Pol oscillators, as is sketched in Figure 1, is considered. Three variable distributions: constant, gaussian and random of the coupling parameter along the ring are proposed. The collective behavior of the ring under the variable distributions is numerically studied and compared with that of a constant distribution. The influence of the oscillator constant on the ring behavior is also considered. Three values of the oscillator constant are assumed, namely 0.1, 0.5 and 1; the dynamic performance of the ring of coupled van der Pol oscillators goes from quasilinear to strongly nonlinear, depending on the kind of coupling distribution.
2. Mathematical Model and Coupling Schemes
The van der Pol oscillator is a well known oscillator which is mathematically represented as
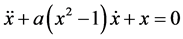 (1)
(1)
where x is the oscillator position and a is the uncoupled oscillator constant. In this work the case of van der Pol oscillators in the form of a ring with each oscillator coupled to its two nearest neighbors is considered. For a ring of N oscillators the following expression holds
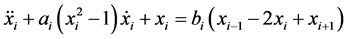 (2)
(2)
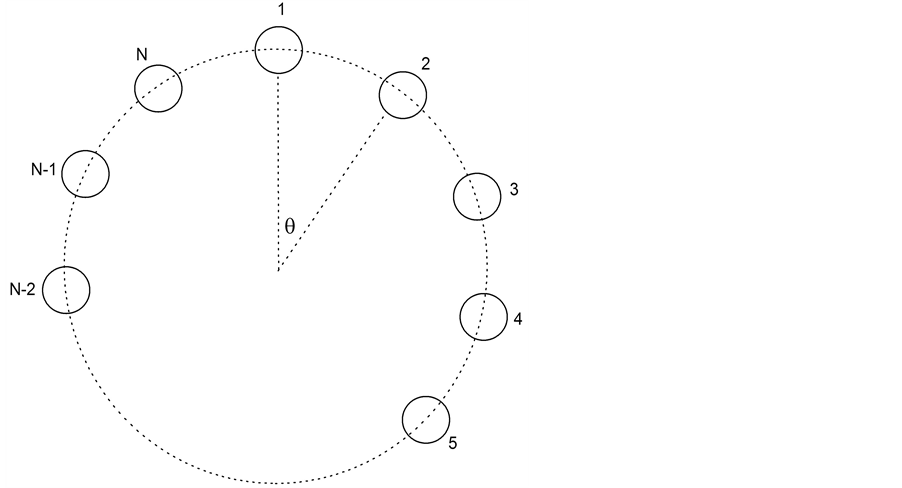
Figure 1. Ring of N coupled oscillators.
where 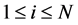 and bi is the coupling parameter corresponding to the ith oscillator, which depends on the angular position θi of the ith oscillator on the ring. Besides,
and bi is the coupling parameter corresponding to the ith oscillator, which depends on the angular position θi of the ith oscillator on the ring. Besides, 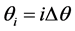 and
and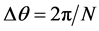 .
.
Given that the coupling parameter depends on the oscillator position in the ring, a coupling vector B can be defined as
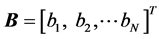 (3)
(3)
For a gaussian distribution of B along the ring, bi is determined from
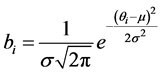 (4)
(4)
where σ is the standard deviation and μ is the mean or expectation of the gaussian distribution.
For a random distribution of the coupling parameter,
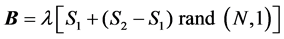 (5)
(5)
where λ, S1 and S2 are constants, and rand (N, 1) is a matrix of random numbers.
For a constant distribution of the coupling parameterB = c (6)
In order to allow a quantitative comparison among the above distributions, all of them must satisfy
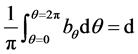 (7)
(7)
where d is a constant. Equation (7) implies that if d = 2, then for a constant distribution in Equation (6) c = d/2 and in this case
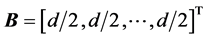 (8)
(8)
3. Numerical Solution
Equation (2) corresponding to the ring of coupled oscillators was numerically solved through the fourth-order Runge-Kutta method [16] . The time step used for integration was 1 × 10−5, which is small enough to guarantee numerical stability and convergence. As in [15] , it was considered that N = 100 is a sufficiently large amount of oscillators for analysis, and that any increase in the amount of oscillators does not change the global behavior of the ring. The Initial conditions for position and velocity of oscillators were determined from [15]
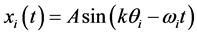 (9)
(9)
where
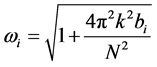 (10)
(10)
Equation (9) represents a wave of amplitude A, wave number k and frequency ω traveling in the positive θ direction. Then, the initial conditions of position and velocity are, respectively, given by
 (11)
(11)
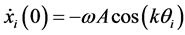 (12)
(12)
In the computer simulations, it was assumed that A = 1, k = 2 and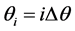 . Identical oscillators were considered in the numerical simulations. Three values of the oscillator constant, namely 0.1, 0.5 and 1, were considered in order to change the dynamic performance of the ring from quasilinear to strongly nonlinear. For N = 100 and d = 2, the following parameter values were defined: 1) for the gaussian distribution σ = 4, μ = 1; 2) for the random distribution λ = 2, S1 = 0, S2 = 2; 3) for the constant distribution c = 1. All these values satisfy the condition given by Equation (7).
. Identical oscillators were considered in the numerical simulations. Three values of the oscillator constant, namely 0.1, 0.5 and 1, were considered in order to change the dynamic performance of the ring from quasilinear to strongly nonlinear. For N = 100 and d = 2, the following parameter values were defined: 1) for the gaussian distribution σ = 4, μ = 1; 2) for the random distribution λ = 2, S1 = 0, S2 = 2; 3) for the constant distribution c = 1. All these values satisfy the condition given by Equation (7).
4. Results and Discussion
Figure 2 and Figure 3 show the histograms corresponding to the gaussian and random distributions of the coupling parameter, respectively. The typical bell-shaped form of a gaussian data distribution is appreciated in Figure 2, whereas an irregular coupling parameter of a random distribution is observed in Figure 3. Both distributions satisfy the condition given by Equation (7). Phase portraits for the three coupling parameter distributions and the three considered values of the oscillators constant were constructed using long term time series of the first and the fifty oscillators. This pair of oscillators was selected because is one of the pairs most apart in the ring.
4.1. Constant Distribution
Figure 4 shows the phase portraits for constant distribution of the coupling parameter for a = 0.1, a = 0.5 and a = 1. The phase portrait of Figure 4(a) corresponds to two time series with equal frequency and a constant phase shift [17] , as is appreciated in the time series of Figure 5(a). The phase portraits of Figure 4(b) and Figure 4(c) come from two time series with multiple frequencies and variable phase shift, as is shown in the time series of Figure 5(b) and Figure 5(c). Uncoupled frequencies of 0.1591, 0.1567 and 0.1500 Hz for a = 0.1, a = 0.5 and a = 1, respectively, are obtained from the power spectra of the long term time series. Coupled frequencies for constant distribution of the coupling parameter, obtained from the respective power spectra, are detailed in the second
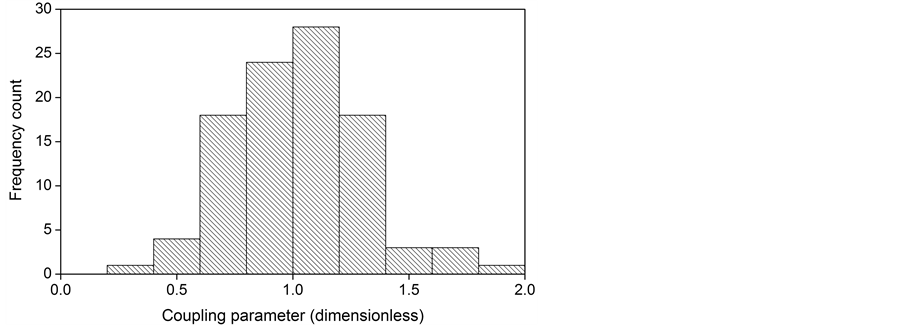
Figure 2. Histogram of the coupling parameter under gaussian distribution.
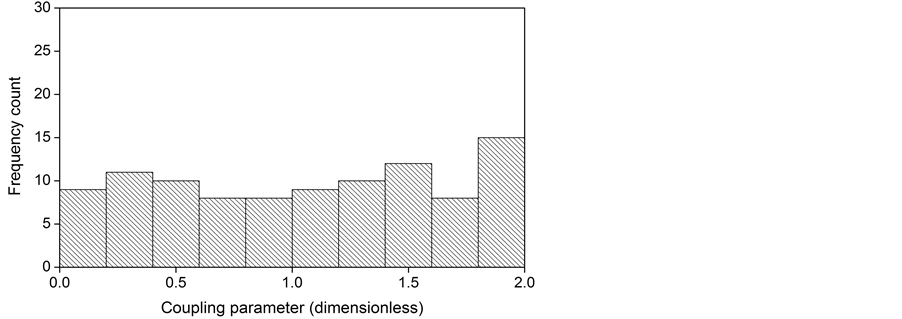
Figure 3. Histogram of the coupling parameter under random distribution.
row of Table 1. For a = 0.1 just one frequency of 0.1603 Hz is present, presumably due to the quasilinear behavior of uncoupled oscillators and the constant distribution of the coupling parameter. For a = 0.5 and a = 1, multiple frequencies are exhibited, being 0.1580 and 0.1526 Hz, respectively, the main frequencies corresponding to these rings. The coupled frequencies are greater than the frequencies corresponding to the uncoupled cases. From Table 1, Figures 4(a)-(c) and Figures 5(a)-(c) is observed that as the oscillator constant is increased, the coupled behavior of the ring becomes more complex given that the nonlinearity of oscillators is increased too. This behavior occurs in spite of the coupling parameter remains constant along the ring.
4.2. Gaussian Distribution
Phase portraits for the gaussian distribution case are depicted in Figures 6(a)-(c). As the oscillator constant is increased, the coupled behavior goes from a single frequency with constant phase shift for a = 0.1 to multiple frequencies with variable phase shift for a = 0.5 and a = 1. Main frequencies of 0.1603, 0.1580 and 0.1525 Hz are identical to those corresponding to the constant distribution case. However, the secondary frequencies are quantitatively different, as can be appreciated when the second and third rows of Table 1 are compared. As in the constant distribution, the dominant frequencies of gaussian distribution are greater than the uncoupled frequencies.
Table 1. Ring frequencies (Hz) obtained from power spectra. Main frequency in bold.
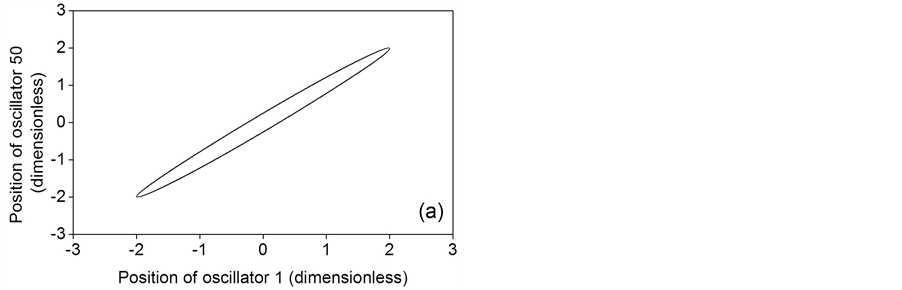

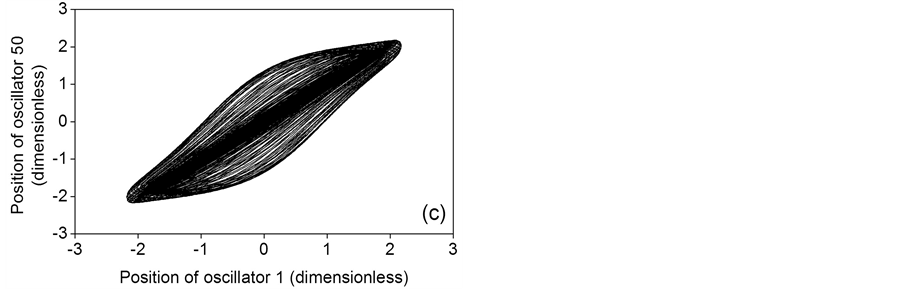
Figure 4. Phase portraits for a constant distribution of the coupling parameter. (a) a = 0.1; (b) a = 0.5; (c) a = 1.
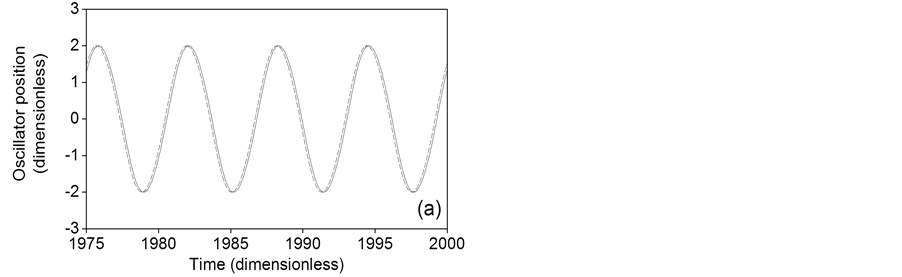
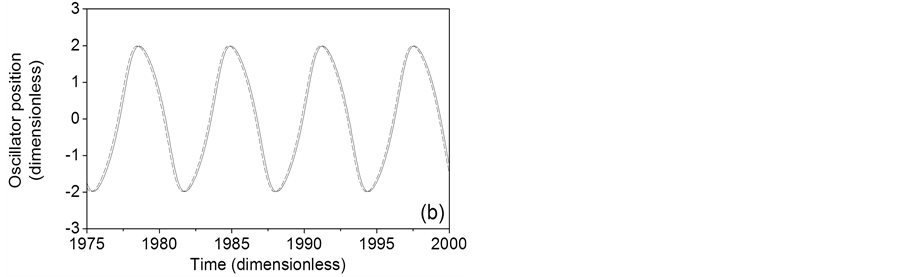

Figure 5. Long time series for a constant distribution of the coupling parameter. (a) a = 0.1; (b) a = 0.5; (c) a = 1. Oscillator 1 (solid), oscillator 50 (dashed).
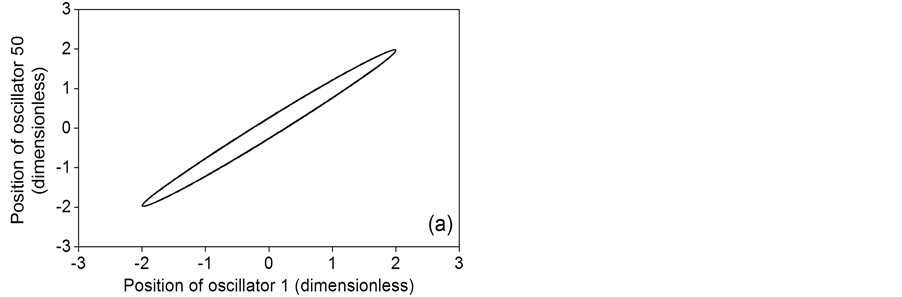
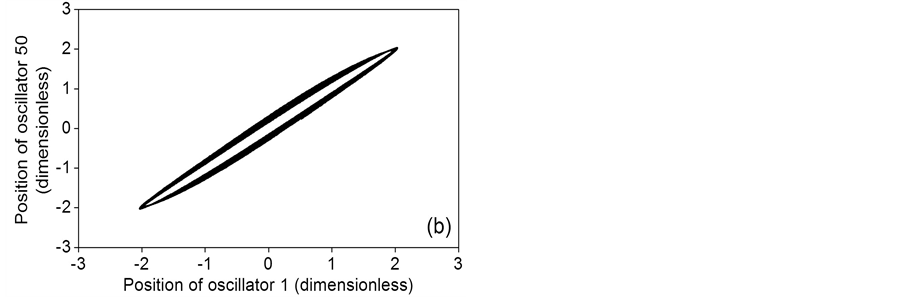
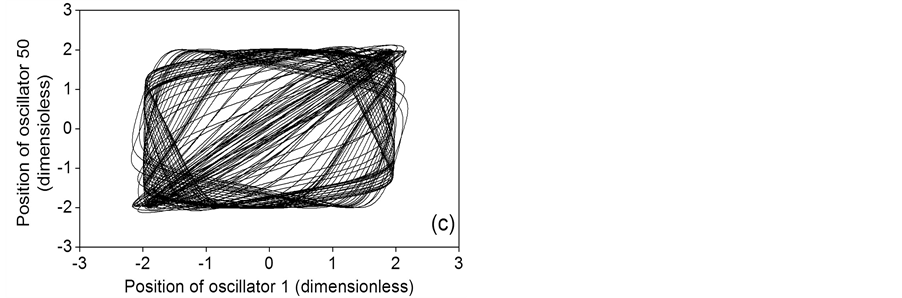
Figure 6. Phase portraits for a gaussian distribution of the coupling parameter. (a) a = 0.1; (b) a = 0.5; (c) a = 1.
4.3. Random Distribution
The phase portraits for random distribution are shown in Figures 7(a)-(c). In accordance to the fourth row of Table 1, main frequencies for a = 0.1, a = 0.5 and a = 1 are 0.1595, 0.1580 and 0.1557 Hz, respectively. Phase portraits of Figure 7(a), Figure 7(b) correspond to anti-phase time series for a = 0.1 and a = 0.5, which exhibit multiple frequencies and variable phase shifts, and can be seen in Figure 8(a) and Figure 8(b), respectively. Phase portrait of Figure 7(c) corresponds to the two chaotic time series [17] of Figure 8(c) for a = 1 whose power spectra are depicted in Figure 9. This dynamic response is due to a combination of the highly disordered random distribution of the coupling parameter and the relatively high value of the oscillator constant, which causes a strong nonlinear behavior of uncoupled oscillators.
4.4. Influence of the Oscillator Constant
The collective behavior of the ring is mainly determined by the nature of the coupling distribution. However, the oscillators’ constant plays also a significant role in this behavior. As the oscillator constant is increased the ring nonlinearity is increased too. For a = 0.1 the coupled performance is little influenced by the coupling distribution, as is observed in the second column of Table 1. In this case, the coupled frequencies of 0.1603, 0.1603 and 0.1591 Hz for constant, gaussian and random distribution, respectively, are very close to the uncoupled frequency of 0.1591 Hz. However, as the oscillator constant is increased from 0.5 to 1, the coupled behavior becomes more complex, and multiple frequencies, anti-phase oscillations and even chaotic oscillations are exhibited, as is appreciated in Figures 6-9.
5. Conclusions
The collective behavior of a ring of coupled identical van der Pol oscillators with different coupling schemes was numerically studied. The nature of this behavior strongly depends on the kind of distribution of the coupling parameter and on the value of the oscillators constant.
1) For a small value of the oscillators constant and a constant distribution of the coupling parameter, the ring behavior goes from quasilinear with a single frequency to multiple frequencies and variable phase shifts.
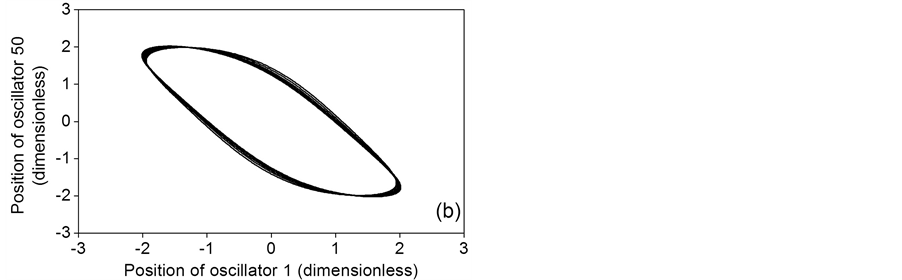


Figure 7. Phase portraits for a random distribution of the coupling parameter. (a) a = 0.1; (b) a = 0.5; (c) a = 1.
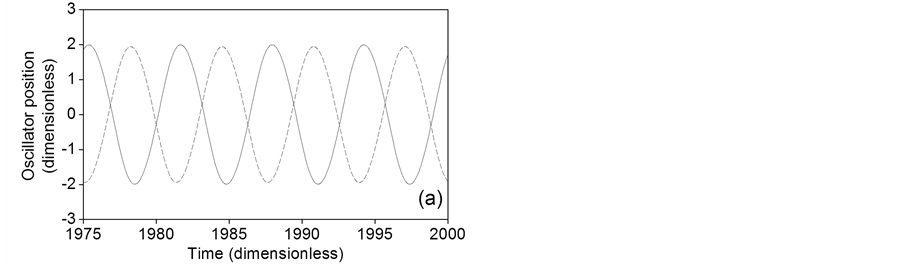
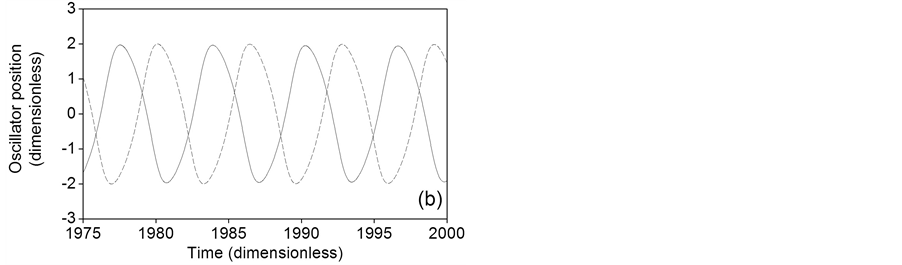
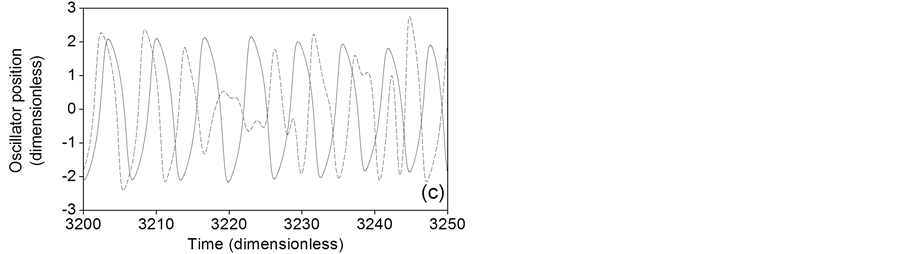
Figure 8. Long time series for a random distribution of the coupling parameter. (a) a = 0.1; (b) a = 0.5; (c) a = 1. Oscillator 1 (solid), oscillator 50 (dashed).
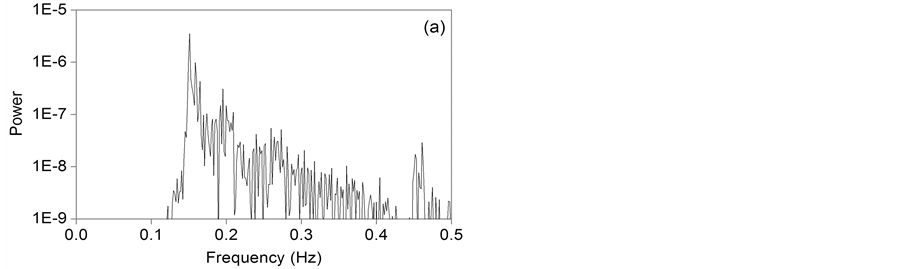

Figure 9. Power spectra of the first (a) and 50th (b) oscillators for a = 1 under a random coupling distribution, corresponding to the time series of Figure 8(c).
2) A random distribution of the coupling constant, combined with a high value of the oscillator constant, causes a coupled behavior which ranges from anti-phase to chaotic.
3) The coupled behavior becomes more complex as the oscillator constant is increased, irrespective of the distribution of the coupling parameter.
4) In the all cases considered, the coupled main frequency is greater that the uncoupled frequency, irrespective of the value of the oscillators constant or the nature of the coupling distribution.
Acknowledgements
M. A. Barron appreciates the generous help and guidance of Prof. Mihir Sen, from Notre Dame University, Notre Dame, IN, during the conception and writing of this paper.
Conflict of Interests
The author declares that there is no conflict of interests regarding the publication of this article.
References
- Winfree, A.T. (1967) Biological Rhythms and the Behavior of Populations of Coupled Oscillators. Journal of Theoretical Biology, 16, 15-42. http://dx.doi.org/10.1016/0022-5193(67)90051-3
- van der Pol, B. and van der Mark, J. (1928) The Heartbeat Considered as a Relaxation Oscillation, and an Electrical Model of the Heart. Philosophical Magazine, 6, 763-775.
- dos Santos, A.M., Lopes, S.R. and Viana, R.L. (2004) Rhythm Synchronization and Chaotic Modulation of Coupled Van Der Pol Oscillators in a Model for the Heartbeat. Physica A, 338, 335-355. http://dx.doi.org/10.1016/j.physa.2004.02.058
- Kuramoto, Y. (1984) Chemical Oscillations, Waves, and Turbulence. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-69689-3
- Camacho, E., Rand, R. and Howland H. (2004) Dynamics of Two Van Der Pol Oscillators Coupled via a Bath. International Journal of Solids and Structures, 41, 2133-2143. http://dx.doi.org/10.1016/j.ijsolstr.2003.11.035
- Aggarwal, J.K. and Richie, C.G. (1966) On Coupled Van Der Pol Oscillators. IEEE Transactions on Circuit Theory, CT13, 465-466. http://dx.doi.org/10.1109/TCT.1966.1082634
- Linkens, D.A. (1976) Stability of Entrainment Conditions for A Particular form of Mutually Coupled Van Der Pol Oscillators. IEEE Transactions on Circuits and Systems, 23, 113-121. http://dx.doi.org/10.1109/TCS.1976.1084184
- Rand, R.H. and Holmes, P.J. (1980) Bifurcation of Periodic Motion in Two Weakly Coupled Van Der Pol Oscillators. International Journal of Non-Linear Mechanics, 15, 387-399. http://dx.doi.org/10.1016/0020-7462(80)90024-4
- Storti, D.W. and Rand, R.H. (1982) Dynamics of Two Strongly Coupled Van Der Pol Oscillators. International Journal of Non-Linear Mechanics, 17, 143-152. http://dx.doi.org/10.1016/0020-7462(82)90014-2
- Storti, D.W. and Rand, R.H. (1986) Dynamics of Two Strongly Coupled Relaxation Oscillators. SIAM Journal of Applied Mathematics, 46, 56-67. http://dx.doi.org/10.1137/0146006
- Pastor, I., Perez, V.M., Encinas, F. and Guerra, J.M. (1993) Ordered and Chaotic Behavior of Two Coupled Van Der Pol Oscillators. Physical Review E, 48, 171-182. http://dx.doi.org/10.1103/PhysRevE.48.171
- Nana, B. and Woafo, P. (2006) Synchronization in a Ring of Four Mutually Coupled Van De Pol Oscillators: Theory and experiment. Physical Review E, 74, 1-8, Article ID: 046213.
- Woafo, P. and Kadji, H.G. (2004) Synchronized States in a Ring of Mutually Coupled Self-Sustained Electrical Oscillators. Physical Review E, 69, 1-9.
- Barron, M.A., Sen, M. and Corona, E. (2008) Dynamics of Large Rings of Coupled Van der Pol Oscillators. In: Elleithy, K., Ed., Innovations and Advanced Techniques in Systems, Computing Sciences and Software Engineering, Springer, Berlin, 346-349. http://dx.doi.org/10.1007/978-1-4020-8735-6_65
- Barron, M.A. and Sen, M. (2013) Dynamic Behavior of a Large Ring of Coupled Self-Excited Oscillators. Journal of Computational and Nonlinear Dynamics, 8, 1-5.
- Chapra, S.C. and Canale, R.P. (2010) Numerical Methods for Engineers. 6th Edition, McGraw-Hill, New York.
- Pikovsky, A., Rosenblum, M. and Kurths, J. (2001) Synchronization, a Universal Concept in Nonlinear Sciences. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511755743


