Open Journal of Applied Sciences
Vol.4 No.4(2014), Article ID:44041,12 pages DOI:10.4236/ojapps.2014.44015
Does the Method of Amalgamation Affect Cost Inefficiency of the New Municipalities?
Katsuyoshi Nakazawa
Department of Economics, Toyo University, Tokyo, Japan
Email: nakazawa@toyo.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 29 January 2014; revised 2 March 2014; accepted 10 March 2014
Abstract
Municipal amalgamation has been done in many countries in recent years as the result of a push to enlarge the size and coverage of local government units, which in turn is driven mainly by the prospect of economies of scale. However, while municipality amalgamation or boundary reform raises population size, it introduces organizational changes in the local government that might increase administrative inefficiency. The choice for the method of integration of administrative functions before amalgamation might affect to public expenditure after amalgamation. This study uses Japanese municipal-level data and argues for a relation between the choice for the method of integration of administrative functions and cost inefficiency after amalgamation. The results show that the fully distributed facility method is more likely to be adopted in a larger administrative jurisdiction and in one with large differences in finances or political structures between amalgamated sub-regions. Moreover, the results of stochastic frontier regression show that new municipality adopting fully distributed facility method can possibly increase inefficiency by expanding organizational slack because the new administration system will be insufficient integration of administrative functions.
Keywords
Amalgamation; Administrative Functions; Multinomial Logistic Regression; Stochastic Frontier Regression; Local Public Expenditure

1. Introduction
Many countries have implemented municipality amalgamation or boundary reform to create larger local governments in order to achieve economies of scale and economies of scope. Local government studies in various countries have confirmed the existence of economies of scale based on population size. However, while municipality amalgamation or boundary reform raises population size, it introduces organizational changes in the local government that might increase administrative inefficiency by an insufficient integration of administrative functions.
In the case of municipal amalgamation in Japan, many municipalities faced the problem of whether administrative functions of the former municipalities should be consolidated in one office building or remain facility across all (ex-) municipalities. Municipalities might obtain residents’ agreement before carrying out amalgamation. If residents feel that they will be inconvenienced by amalgamation, they will presumably oppose it. Thus, municipalities before amalgamation might consider the method of integrating administrative functions.
From the perspective of economies of scale, it might seem clear that the fully consolidation is an advantage. On the other hand, new municipalities might prefer to distribute administrative functions for the convenience of residents in each former district. Municipality amalgamation adopting more distributed facility method can possibly increase inefficiency by expanding organizational slack because the new administration system will be geographically scattered and need more staffs. Therefore, the choice for the method of integration of administrative functions before amalgamation might affect the cost inefficiency of municipalities after amalgamation.
Research on local government inefficiency commonly applies the stochastic frontier cost function to local government expenditure (e.g., Kumbhakar and Lovell [1] , for a discussion of frontier analysis). Previous studies have focused on different local government structures. Deller and Rudnicki [2] ; Couch, Shughart, and Williams [3] ; Battese and Coelli [4] ; Duncombe, Miner, and Ruggiero [5] ; and Kan and Greene [6] focused on the US school district. Davis and Hayes [7] focused on US police. Grosskopf and Yaisawarng [8] developed a multiproduct model of municipalities in California. Grossman, Mavros, and Wassmer [9] focused on large US cities. Kalseth and Rattø [10] estimated the Norwegian local per capita total budget. Loikkanen and Susiluo [11] focused on Finnish municipalities’ cost inefficiency of basic welfare service provision. Yamashita, Akai, and Sato [12] ; Hayashi [13] ; and Miyazaki [14] estimated Japanese cities’ total expenditure. Moreover, Nakazawa [15] estimated Japanese municipalities’ expenditure after amalgamation and shows that municipality amalgamation produces integration costs (slack) in an administrative organization.
In this paper, I consider the factors that might affect the choice for the method of the distribution of public facilities and services in the new municipality using the multinomial logistic regression. Moreover, I apply the stochastic frontier cost function to evaluate the cost inefficiency of Japanese municipalities after amalgamation. In this way, this paper examines how the choice for service distribution method affects the cost inefficiency of municipal expenditures after amalgamation.
This paper is organized as follows. Section 2 gives background on Japanese municipal amalgamation and distribution of services. Section 3 presents empirical method and hypothesis. Section 4 explains data and descriptive statistics. Section 5 conducts a multinomial logistic analysis using municipal data to examine the choice for the method of the distribution of public facilities and services in the new municipality before amalgamation. Then I estimate municipal expenditures’ cost inefficiency after amalgamation using the stochastic frontier cost function. Section 6 concludes the paper.
2. Municipality Amalgamation in Japan
The number of Japanese municipalities almost halved, from 3229 to 1719, between April 1999 and January 2012. According to the Japanese Ministry of Internal Affairs and Communications (MIC) [16] , amalgamation was promoted to establish suitable administrative and fiscal foundations for a basic-model municipality. In other words, MIC aimed to strengthen the financial condition of municipalities by enlarging their scale (the “economies of scale” argument).
Amalgamation was rapid but not without problems. In a national survey by Japan City Center [17] , a public interest incorporated foundation for research of local government, 68.5% of amalgamated municipalities agreed that “Public office buildings have become far away and become inconvenient” as a result of amalgamation, and 54.1% that “The difference between the central area and the region surrounding has expanded”, making these the most commonly identified issues1. The choice of the location of the central municipal administration office and the method of distributing administrative functions often became a big problem. Location and distribution of public offices within a municipality after amalgamation was often planned with the need to win the support of residents in mind.
There were three methods of integrating municipal integrating administrative functions by location. The current investigation considers only administrative services, not basic services such as public library, fire, etc.
The “fully centralized method” (Method 1, henceforth) consolidates all administrative functions into one public office building, mothballing other former facilities. This method seems good from the perspective of economies of scale; however, access to services becomes less convenient for many residents. In many cases, the municipality opens some branch offices that provide specific service (e.g., resident registration and the acceptance of the document, etc.) to ease the access of the resident of former municipalities where the new central public office building was not set up.
The “multiple independent facilities method” (Method 2, henceforth) involves the distribution of various facilities across various locations. One former public office building is chosen as the central building in a new municipality, departments of administrative functions are allocated to the other former public buildings. For example, the department of management and the department of resident registration are distributed to a former public building, the department of welfare and health is distributed the other former public building. This method consolidates each department function into one public office building, but still an inconvenience for people who need to access a service that is not located in their area.
The “fully distributed facility method” (Method 3, henceforth) consolidates council and senior administration in one central building, but maintains all other services in the same distribution as before amalgamation. Thus, it achieves maximum convenience at the expense of consolidation.
From the perspective of economies of scale, Method 1 is obviously the best choice, just as from the perspective of convenience, it is clearly the worst. On the other hand, Method 3 is obviously the best choice to ease the transition to new municipal, but the arrangement of the business and the staff is not efficient because an administrative organization has been left as before amalgamation. In the following sections, I estimate the choice for the method of the distribution of public facilities and services in the new municipality by multinomial logistic regression and examine the effect of these methods on the cost inefficiency of municipalities after amalgamation using stochastic frontier regression.
3. Empirical Approach
3.1. Multinomial Logistic Regression
I use multinomial logistic regression, because this paper is dealing with multiple (three) facility methods. I assume the choice of facility distribution method to be J and the selection result to be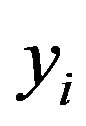 . For amalgamated municipality i with regional characteristics
. For amalgamated municipality i with regional characteristics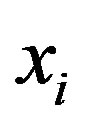 , I find probability
, I find probability  of selecting method j, as follows.
of selecting method j, as follows.
 (1)
(1)
This mathematical form can be transformed by generalizing, as follows.
 (2)
(2)
Then, I estimate the following log-likelihood functions.
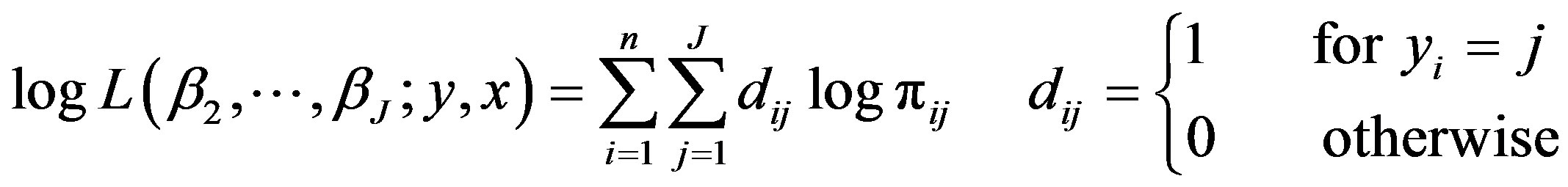 (3)
(3)
Each method given above has advantages and disadvantages. Method 3 might be preferable for a municipality is greatly expanding the geographical area over which it has amalgamation. In contrast, when a municipality with a large population is participating in the amalgamation, a new municipality after amalgamation might consolidate administrative functions in one building. Moreover, the method might change depending on the number of municipalities and the political difficulty of each municipality participating in amalgamation. I adopt the following variables for regional characteristic vector xi of the amalgamating municipalities.
First, I consider demographic and geographic factors. The expansion of the size of a jurisdiction by amalgamation gives an incentive to distribute administrative functions. Thus, I adopt the area of the municipality after amalgamation (area) as a variable. When a municipality with a large population and one with a small population scale amalgamate, the utility of consolidating the administrative functions in the (ex-) municipality with a large population (i.e., in that section of the amalgamated population) is high. Thus, I also adopt the ratio of the population in the ex-municipality whose population is the largest before amalgamation to the population of the municipality after amalgamation (r_pop). Next, when the population is relatively elderly, the likelihood is strong that decentralization will be preferred to secure accessibility for the elderly. Thus, I adopt elderly ratio in the municipality after amalgamation (r_o65).
Second, I consider the factors related to the difficulty of the negotiations among municipalities. An increase in the number of municipalities participating in a potential amalgamation has the possibility of complicating the successful conclusion of an agreement to amalgamate. In contrast, there might be a higher possibility of conflicts of interest in an amalgamation involving a smaller number of municipalities. I check whether the number of municipalities (nm) participating in amalgamation influences the distribution of facilities. Moreover, I take the number of days of negotiations for amalgamation (n_term) as an index showing the difficulty of the negotiations. Finally, I adopt as a dummy variable the political parties to which the mayors of the amalgamating municipalities belong (d_poli). This variable takes 1 when there is a difference in party membership present.
Third, I consider the financial differences between municipalities. I adopt three variables related to differences in financial conditions between municipalities. The financial capacity index is the ratio of expected fiscal revenues to standard fiscal demands. It shows the level of financial resources available within the municipality. I use the standard deviation of the financial capacity index in each municipality before amalgamation (fci_sd). Then, I adopt the standard deviation of public debt per capita (pdebt_sd) as a second financial variable. Finally, I adopt the standard deviation of income per capita (income_sd). When these variables are large, it means that economic and financial differences between municipalities before amalgamation are large.
Finally, I consider the type of amalgamation. Municipal amalgamation in Japan has taken two forms: absorption, in which one municipality absorbs others; and consolidation, where the municipalities amalgamate equally and create a new composite municipality. Absorption might be more likely than consolidation to adopt Method 1, since a single centralized facility makes more sense where one ex-municipality maintains dominance in the new entity. For this study, I adopt type of amalgamation as a dummy variable taking 1 when municipality chooses consolidation (d_conso).
3.2. Stochastic Frontier Cost Function
A stochastic frontier regression is typically formulated as follows:
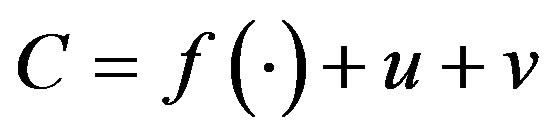 (4)
(4)
C is the local public expenditure, and 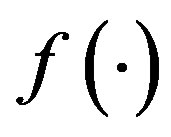 is the cost function of local public expenditure generated from economic theory; v is a standard disturbance term,
is the cost function of local public expenditure generated from economic theory; v is a standard disturbance term,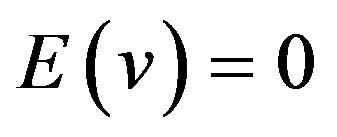 ; u is a stochastically distributed technical inefficiency variable, which is truncated below zero according to the standard practice for cost functions.
; u is a stochastically distributed technical inefficiency variable, which is truncated below zero according to the standard practice for cost functions.
First, I consider the production process of the local public good. The local government inputs the production input vector and produces the direct output (D-output, g), which, however, I cannot observe directly. Then, g is converted to the public services level z, which the residents finally consume (C-output). The vector x of municipality characteristics is assumed to influence the conversion process from D-output to C-output.
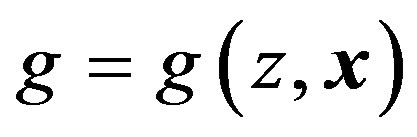 (5)
(5)
Second, when (5) is substituted for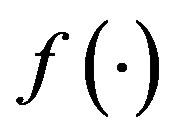 , the cost function is shown as follows.
, the cost function is shown as follows.
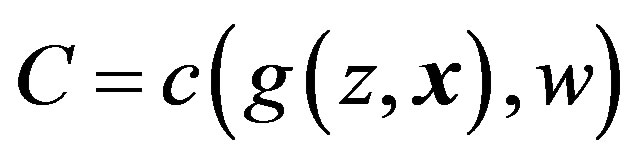 (6)
(6)
where w is the price of the production input.
Then, I estimate the cost function, which I assume is of the Cobb-Douglas form; capital and labor are the production inputs. Thus, the price of the production input is the price of capital r divided by the price of labor w. The cost function is shown in a log-linear form as follows:
 (7)
(7)
I assume that the price of capital r is not different between municipalities (Brueckner [18] ). Thus, r is included at the constant term.
 (8)
(8)
The D-output g is transformed to a log-linear form as follows:
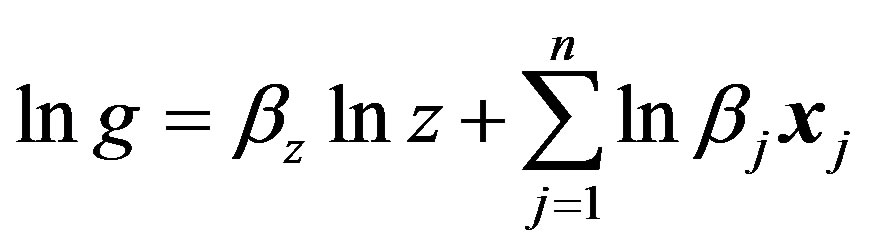 (9)
(9)
Population size and area are the fundamental factors of municipality characteristics (vector x). I assume economies as well as diseconomies (congestion) of population size in the consumption process of public goods. I adopt the square of the population size. I also employ variables for the demographic structures of the municipality. Finally, substituting (9) into (8), I show the stochastic frontier cost function for each municipality as follows.
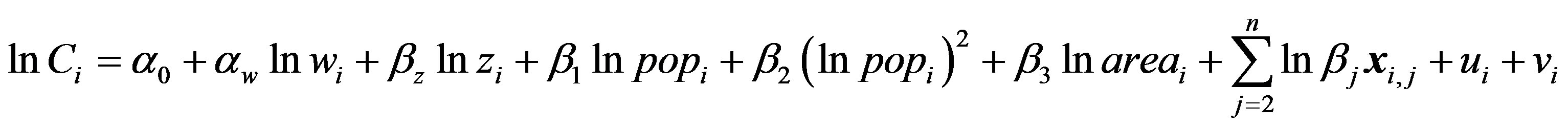 (10)
(10)
3.3. C-Output Index and Inefficiency Factors
Recent estimates of the local public cost function use “Total score of public services”, prepared by Nihon Keizai Shinbunsya as the C-output z (Yamashita, Akai, and Sato [12] ; Hayashi [13] ). However, this index has a problem in that it is constructed only for cities. When this index is used, a lot of dropouts are caused in the sample because municipalities after amalgamation include many towns and villages. Miyazaki [14] established a new index that can be applied to towns and villages: “Total score of public services”. This paper uses Miyazaki’s method to construct index z. The calculation method is shown as follows.
C-output index is composed of five sub-indexes Aged care, Child care, Education, Life infrastructure, and Safety. These sub-indexes are weighted 30, 35, 25, 40, and 20, respectively, and include components that provide an index for each category of public service. The numerical values of weights of these sub-indexes are referred from the “Total score of public services”. All components are converted to their deviation values.
 (11)
(11)
where y1 represents the number of doctors divided by the elderly population, y2 the capacity in welfare facilities for the elderly divided by the elderly population, y3 the capacity of healthcare facilities divided by the elderly population, y4 the capacity of sanatorium-type medical care facilities divided by the elderly population, y5 the enrollment in kindergartens and day nurseries divided by the 0- to 4-year-old population, y6 the number of children on day nursery waiting-lists divided by the enrollment in day nurseries, y7 the number of elementary school teachers divided by number of elementary school students, y8 the number of junior high school teachers divided by number of junior high school students, y9 the number of community centers divided by the population, y10 the total road length (km) divided by the area (km2), y11 the number of people who disposed of general household garbage divided by the population, and y12 the number of fire occurrences divided by the population. All data are for FY2010.
This paper employed two technical inefficiency variables related to the consequence of the choice of the methods. One is a dummy variable for the Method 2 (d_Method_2). The other is a dummy variable for the Method 3 (d_Method_3). Municipality amalgamation adopting distribution administrative functions can possibly increase inefficiency by expanding organizational slack because the new administration system will be geographically scattered. Thus, the choice of the distribution amalgamation method might also affect slack costs after amalgamation.
4. Data
I consider amalgamating Japanese municipalities from FY 2000 to FY 2005.The analysis object is 479 amalgamated municipalities that contain 1176 ex-municipalities. Thus, I employ the explanatory variables given above for FY 2000 in the multinomial logistic regression. From the Amalgamation Digital Archive by MIC, 138 of these municipalities (29%) adopted Method 1, 115 (24%) adopted Method 2, and 226 (47%) adopted Method 3.2
In the stochastic frontier regression, I employ the variables given above for FY 2010 to estimate municipal expenditure since it is the latest data that can be used. This paper employs two type of cost . One is the total local public expenditure of the municipalities that amalgamated. The other is the total public expenditure that excludes public investment expenditure and public debt repayment expenditure of the municipalities that amalgamated. It seems that slack costs of amalgamation would mainly apply to operating expenses. The explanatory valuable
. One is the total local public expenditure of the municipalities that amalgamated. The other is the total public expenditure that excludes public investment expenditure and public debt repayment expenditure of the municipalities that amalgamated. It seems that slack costs of amalgamation would mainly apply to operating expenses. The explanatory valuable  is calculated according to the procedure described in Section 3.3. The labor cost of public services
is calculated according to the procedure described in Section 3.3. The labor cost of public services 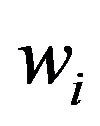 is obtained as the average labor cost, calculated by dividing the total public labor cost of the municipality by the number of public employees. Population
is obtained as the average labor cost, calculated by dividing the total public labor cost of the municipality by the number of public employees. Population 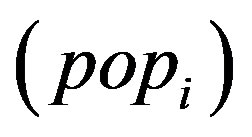 and area
and area 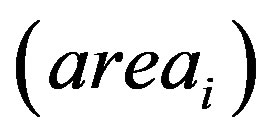 data of the municipality are from the National Census. The variable of demographic characteristics
data of the municipality are from the National Census. The variable of demographic characteristics 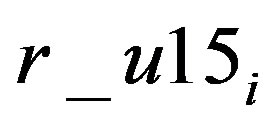 is the ratio of the 15-and-under population to total population,
is the ratio of the 15-and-under population to total population, 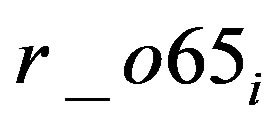 is the ratio of the 65-and-older population to total population. These variables control the difference of residents’ demand for public services. These data are also from the National Census. The data used for the estimation are described as follows with their source and the descriptive statistics in Table 1.
is the ratio of the 65-and-older population to total population. These variables control the difference of residents’ demand for public services. These data are also from the National Census. The data used for the estimation are described as follows with their source and the descriptive statistics in Table 1.
5. Estimation Results
5.1. Multinomial Logistic Regression
First, I assess facility distribution method in the amalgamated municipalities using cross-section multinomial logistic regression. I use Method 2 (multiple independent facilities method) as a base outcome and report coefficient and relative risk ratio (rrr). Estimation results are shown in Table 2.
Table 1. Descriptive statistics and data sources.
Sources: A: National Census, B: Amalgamation Digital Archive, C: Nationwide Mayor’s List, D: Local Government Finance Settlement, E: Tax Investigation for Municipalities, F: Statistic Bureau, Ministry of Internal Affairs and Communications, G: Statistic Bureau, Ministry of Health, Labour and Welfare.
Table 2. Estimation results of multinomial logistic regression.
Note: Base outcome is that for Method 2. The asterisks ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.1 levels, respectively.
Simultaneously, to approve the multinomial logistic regression, I test Hausman’s independence from irrelevant alternatives (IIA) assumption. The result supports the use of multinomial logistic regression. The hypothesis (H0) of Hausman’s IIA test of odds is independent of the other alternatives. Hausman’s IIA test results all support the H0. Thus, the use of multinomial logistic regression is approved3.
I observe that the size of geographic area of post-amalgamation municipality is likely to choose Method 3. Figure 1 shows that the expansion of the administrative jurisdiction of a municipality improves the probability of the selection of a decentralized model involving integrate branch offices. Correspondingly, the selection probability of Method 1 decreases with the expansion of the area.
The probability to choose Method 1 and Method 3 are higher than Method 2 when r_pop is high. In addition, the relative risk ratio of Method 1 is higher than that for Method 3. When a municipality with a large population and one with a small population amalgamate, the likelihood that administrative functions will be consolidated in the municipality with a large population is high. Figure 2 shows selection probability and r_pop for each of these methods. Method 3 is consistently high, but selection probability for Method 1 improves as r_pop increases (while that for Method 2 declines). This also supports the choice to make the consolidation dummy (d_conso) is less likely to choose Method 1.
The probability to choose Method 1 and Method 3 are higher than Method 2 when r_o65 is high. Here, the relative risk ratio of Method 3 is higher than that of Method 1. The probability to choose Method 1 and Method 3 are higher than Method 2 as the number of municipalities participating in amalgamation (nm) increases. One
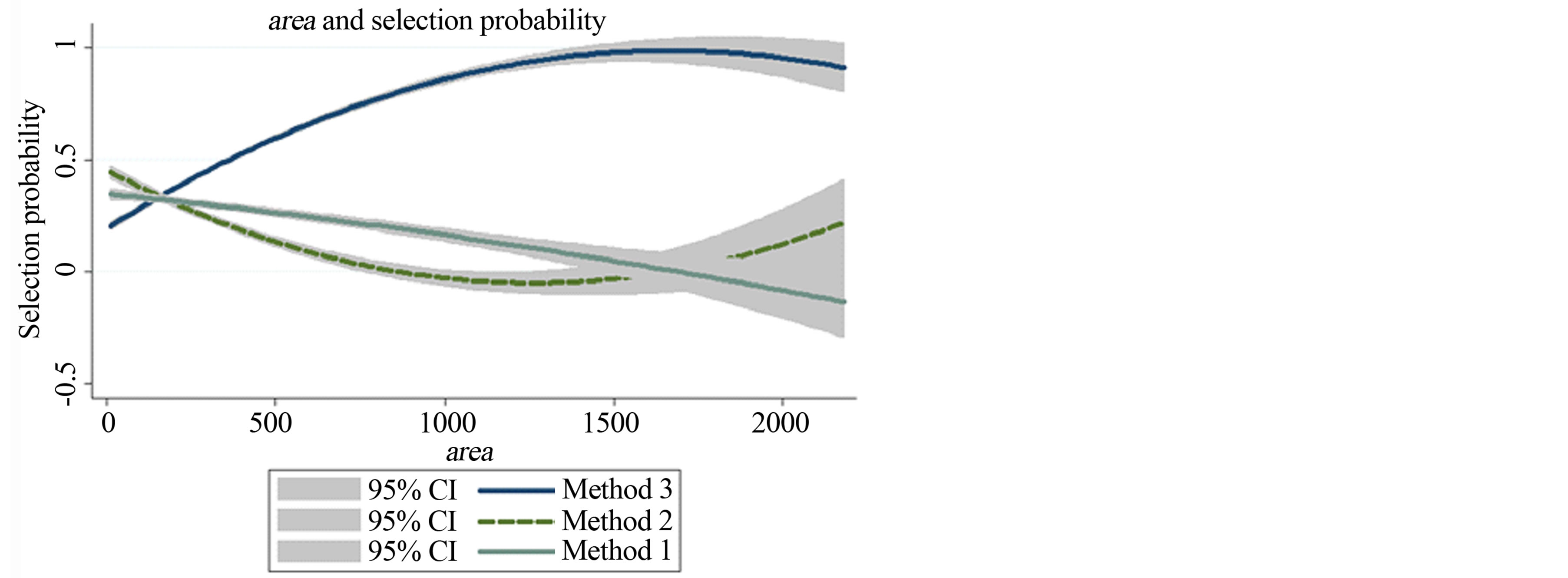
Figure 1. Area and selection probability.

Figure 2. r_pop and selection probability.
explanation could be the result for Method 1. A municipality with a large population often absorbs many small municipalities. Figure 3 shows selection probability and nm. The selection probability of Method 3 increases with an increasing number of municipalities participating in amalgamation.
The probability to choose Method 1 and Method 3 are higher than Method 2 as the number of days of negotiations for amalgamation (n_term) increases. Figure 3 shows, however, that the strength of the influence varies. The selection probability of Method 2 decreases in a linear fashion as the amount of negotiation increases. Also, the effect of the mayors of amalgamating municipalities’ belonging to different political parties (d_poli) is strong for Method 3, meaning that it tends to promote a decentralized method.
Difference in fiscal condition between municipalities before amalgamation increases the probability to choose Method 1 and Method 3 compared to Method 2, and relative risk ratio of fci_sd for Method 3 is higher than that for Method 1. However, income_sd does not affect selection probability in any methods.
I can summarize the above results as follows. Method 1 has a tendency to be selected when a larger municipality in population scale absorbs other municipalities—in other words, when the magnitude correlation between municipalities that amalgamate is clear. Method 2 has a tendency to be selected when amalgamation is small scale or when the difference in socioeconomic conditions between municipalities before amalgamation is small. Finally, Method 3 has a tendency to be selected when large financial and political differences exist between municipalities or when the jurisdiction becomes large and access to the public buildings becomes more difficult as a result.
Thus, in short, the method by which provision of public facilities is organized in post-amalgamation municipalities is affected by demographical, geographical, socioeconomic, and political differences among municipalities before amalgamation.
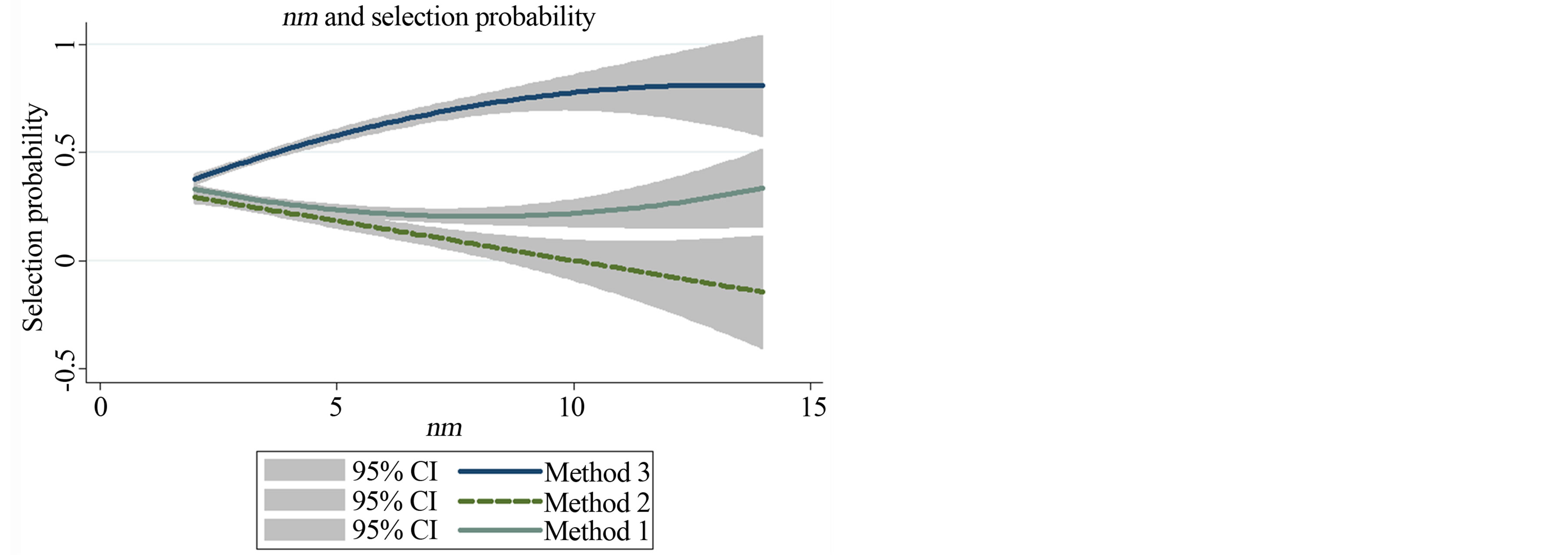
Figure 3. nm and selection probability.
5.2. Stochastic Frontier Cost Function
This paper employs two types of estimation. The first is the ordinary least squares (OLS) regression excluding inefficiency variables. OLS regression is the base model for comparison with stochastic frontier estimation results. The second is the stochastic frontier estimation incorporating inefficiency variables. The OLS test for heteroskedasticity is implemented with Heteroscedasticity-Consistent Standard Errors (HCSEs). The stochastic frontier estimation uses the maximum likelihood (ML) method with the half-normal distribution as the distribution of inefficiency term. As described above, this paper chooses two types of public expenditure. One is the total local public expenditure of the municipalities that amalgamated. The other is the total public expenditure that excludes public investment expenditure and public debt repayment expenditure. Estimation results are shown in Table 3.
First, I examine the estimation results of the total local public expenditure. On a comparison of the OLS regression with the stochastic frontier estimation result, the parameters of  is insignificant for the OLS result. On the other hand, the parameters of the stochastic frontier estimation are all significant and appropriate in economic theory. The parameter of
is insignificant for the OLS result. On the other hand, the parameters of the stochastic frontier estimation are all significant and appropriate in economic theory. The parameter of  is significantly positive. Local government expenditure increases as public service output increases. Compared to the OLS regression result, the influence of
is significantly positive. Local government expenditure increases as public service output increases. Compared to the OLS regression result, the influence of 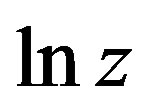 is excessively evaluated in the OLS regression. The parameter of
is excessively evaluated in the OLS regression. The parameter of  is significantly positive at the 10% level. The low significance level of this parameter can probably be explained by the fact that the average labor cost for public employees was used as an index. The average labor cost for public employees depends on the number of staff and the age distribution of the municipality. The parameter of
is significantly positive at the 10% level. The low significance level of this parameter can probably be explained by the fact that the average labor cost for public employees was used as an index. The average labor cost for public employees depends on the number of staff and the age distribution of the municipality. The parameter of 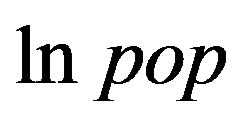 is significantly negative and that of
is significantly negative and that of  is significantly positive. These results show that the relationship between total public expenditure and population size describes a U-shaped curve for the municipalities after amalgamation. Thus, these municipalities have both economies and diseconomies (congestion) of population size for total public expenditures. The other geographic and demographic characteristics are significantly positive. These variables work as costpushing factors.
is significantly positive. These results show that the relationship between total public expenditure and population size describes a U-shaped curve for the municipalities after amalgamation. Thus, these municipalities have both economies and diseconomies (congestion) of population size for total public expenditures. The other geographic and demographic characteristics are significantly positive. These variables work as costpushing factors.
The inefficiency variables d_Method_2 is not significant but d_Method_3 is significantly positive. Municipality amalgamation adopting decentralized administrative functions can possibly increase inefficiency. Therefore, municipality amalgamation causes integration costs (slack) for an administrative organization when the municipality chooses decentralized administrative functions method.
Second, I examine the estimation results for the total public expenditure that excludes public investment expenditure and public debt repayment expenditure. With 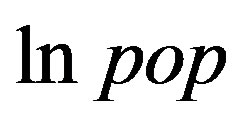 excluded, both results are significant and appropriate in economic theory. Public investment expenditure strongly reflects economies of scale and public debt is allotted to public investment. Thus, the total public expenditure that excludes public investment expenditure and public debt repayment expenditure is hard to be reflected economies of scale. The results of the inefficiency variables are the same for the estimation results of the total local public expenditure.
excluded, both results are significant and appropriate in economic theory. Public investment expenditure strongly reflects economies of scale and public debt is allotted to public investment. Thus, the total public expenditure that excludes public investment expenditure and public debt repayment expenditure is hard to be reflected economies of scale. The results of the inefficiency variables are the same for the estimation results of the total local public expenditure.
The average technical efficiency scores of total public expenditure and the total public expenditure that excludes public investment expenditure and public debt repayment expenditure are 1.167 and 1.150, respectively. This means that, on average, 16.7% of the total public expenditure and 15% of the total public expenditure
Table 3. OLS and stochastic frontier estimation result.
Note: The asterisks ***, **, and * indicate statistical significance at the 0.01, 0.05, and 0.1 levels, respectively.
that excludes public investment expenditure and public debt repayment expenditure are wasted. That is to say, municipalities can potentially reduce these costs by 16.7% and 15%, respectively, after amalgamation, maintaining the same level of public services. However, municipality amalgamation, if not followed by administrative reorganization and efficiency improvement, would create sustained administration slack, leading the cost inefficiency of municipal expenditure.
6. Conclusions
Economies of scale are believed to promote municipal amalgamation. However, amalgamation is enlarging population scale and various kinds can interfere with the achievement of economies of scale. In the case of Japanese municipality amalgamation, location and distribution of public offices within a municipality after amalgamation were often planned with the need to win the support of residents in mind. Thus, the method by which provision of public facilities is organized in post-amalgamation municipalities is affected by demographical, geographical, socioeconomic, and political differences among municipalities before amalgamation. Moreover, the choice affects the cost inefficiency of municipalities after amalgamation. Especially, the more decentralized method can potentially create inefficiency by increasing organizational slack cost caused from an insufficient integration of administrative functions.
This paper examined the effect of differences in facility distribution methods on municipal cost inefficiency after amalgamation. I estimated multinomial logistic regressions for three such methods and found that expansion of administrative jurisdiction, large differences in demographical, geographical, socioeconomic, and political differences among municipalities before amalgamation between amalgamating municipalities improve the probability of the selection of a decentralized method.
Then, this paper examined the cost inefficiency of municipalities after amalgamation, using stochastic frontier cost estimation. Using OLS to estimate the local public cost function of municipalities after amalgamation might lead to miss-specified results because of the exclusion of inefficiency terms resulting from the amalgamation. With the elimination of inefficiency terms, the other variables might be either underestimated or overestimated. The inefficiency terms are significantly positive for all estimations. From this result, more decentralized methods had the effect of pushing up inefficiency of the local public expenditure after amalgamation. In other words, the local public expenditure of municipalities after amalgamation is related to the distribution of services agreed on by municipalities before amalgamation. Thus, this paper shows that amalgamation might lead to cost inefficiency due to administrative slack even as it creates economies of population scale. This slack might be called “administrative adjustment costs after amalgamation”.
Acknowledgements
This paper is a revised and expanded version of a paper entitled “Cost Inefficiency of Municipalities after Amalgamation” presented at International Conference on Applied Economics (ICOAE2013), Istanbul, 27-29 June, 2013.
References
- Kumbhakar, S.C. and Lovell, C.A.K. (2000) Stochastic Frontier Analysis. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139174411
- Deller, S.C. and Rudnicki, E. (1992) Managerial Efficiency in Local Government: Implications on Jurisdictional Consolidation. Public Choice, 74, 221-231. http://dx.doi.org/10.1007/BF00140769
- Couch, J.F., William, F., Shughart, I. and Williams, A.L. (1993) Private School Enrollment and Public School Performance. Public Choice, 76, 301-312. http://dx.doi.org/10.1007/BF01053301
- Battese, G.E. and Coelli, T.J. (1995) A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data. Empirical Economics, 20, 325-332. http://dx.doi.org/10.1007/BF01205442
- Duncombe, W., Miner, J. and Ruggiero, J. (1997) Empirical Evaluation of Bureaucratic Models of Inefficiency. Public Choice, 93, 1-18. http://dx.doi.org/10.1023/A:1017910714756
- Kan, B. and Greene, K.V. (2002) The Effects of Monitoring and Competition on Public Education Outputs: A Stochastic Frontier Approach. Public Finance Review, 30, 3-26. http://dx.doi.org/10.1177/109114210203000101
- Davis, M.L. and Hayes, K. (1993) The Demand for Good Government. Review of Economics and Statistics, 75, 148- 152. http://dx.doi.org/10.2307/2109639
- Grosskopf, S. and Yaisawarng, S. (1990) Economies of Scope in the Provision of Local Public Services. National Tax Journal, 43, 61-74.
- Grossman, P.J., Mavros, P. and Wassmer, R.W. (1999) Public Sector Technical Inefficiency in Large U.S. Cities. Journal of Urban Economics, 46, 278-299. http://dx.doi.org/10.1006/juec.1998.2122
- Kalseth, J. and Rattø, J. (1995) Spending and Overspending in Local Government Administration: A Minimum Requirement Approach Applied to Norway. European Journal of Political Economy, 11, 239-251. http://dx.doi.org/10.1016/0176-2680(94)00063-P
- Loikkanen, H.A. and Susiluoto, L. (2005) Cost Efficiency of Finnish Municipalities in Basic Service Provision 1994- 2002. Urban Public Economics Review, 4, 39-63.
- Yamashita, K., Akai, N. and Sato, M. (2002) Effects of Incentives Lurking in the Local Allocation Tax Grant System: Analysis of the Soft Budget Constraint Problem Based on the Frontier Cost Function (Chihou Kouhu Zei Seido ni Hisomu Incentive Kouka: Frontier Hiyou Kansuu ni yoru Soft na Yosa Seiyaku no Kensyou). Financial Review (Ministry of Finance, Policy Research Institute), 61, 120-145. (In Japanese)
- Hayashi, M. (2002) Local Characteristics and Inefficiencies in Local Public Expenditure (Jititai Tokusei to Hikouritusei). The Bulletin of Institute for Research in Business and Economics Meiji Gakuin University, 19, 15-21. (In Japanese)
- Miyazaki, T. (2006) Installation of Legal Conference and Efficiency of Municipality: In Association with Special Mergers Law in 1999 (Kouritu-teki Jititai ni yoru Houtei Kyougikai no setti: 1999 nen Gappei Tokurei Hou to Kannrenn site). Japan Economic Studies (Nihon Keizai Kenkyuu), 54, 20-38. (In Japanese)
- Nakazawa, K. (2013) Cost Inefficiency of Municipalities after Amalgamation. Procedia Economics and Finance, 5, 581-588. http://dx.doi.org/10.1016/S2212-5671(13)00068-3
- Ministry of Internal Affairs and Communication (2010) Publication about the Great Amalgamation. (In Japanese) http://www.soumu.go.jp/gapei/pdf/100311_1.pdf
- Japan City Center (2008) Questionnaire Survey for Amalgamation Municipality. (In Japanese) http://www.toshi.or.jp/gappei/syukeikekka.pdf
NOTES

1Multiple answers were allowed.

2Ministry of Internal Affairs and Communications, Amalgamation digital archive: http://www.gappei-archive.soumu.go.jp/. Accessed 2013 Feb 12.

3In addition, I tested alternative IIA test using Small–Hsiao tests. The results of the tests all support the H0.


