Open Journal of Applied Sciences
Vol.3 No.1(2013), Article ID:29366,7 pages DOI:10.4236/ojapps.2013.31001
Analysis of Nonlinear Stochastic Systems with Jumps Generated by Erlang Flow of Events
Department of Mathematical Cybernetics, Moscow Aviation Institute, Moscow, Russia
Email: *rkoffice@mail.ru
Received December 2, 2012; revised January 2, 2013; accepted January 9, 2013
Keywords: Analysis; Erlang Flow of Events; Generalized Fokker-Planck Equations; Random Impulses; Jump-Diffusion Process; Spectral Characteristic; Spectral Method Formalism; Stochastic System
ABSTRACT
In this paper we consider the stochastic systems with jumps (random impulses) generated by Erlang flow of events that lead to discontinuities in paths. These systems may be used in various applications such as a control of complex technical systems, financial mathematics, mathematical biology and medicine. We propose to use a spectral method formalism to the probabilistic analysis problem for the stochastic systems with jumps. This method allows to get a solution of the analysis problem in an explicit form.
1. Introduction
In this paper we consider the stochastic systems with jumps generated by Erlang flow of events that lead to discontinuities of sample paths. These systems are called the jump-diffusion systems or the stochastic systems with random quantization period. Jumps may have different characteristics that describe intervals between them and their amplitudes [1,2].
Stochastic systems with jumps are used in various applications such as complex technical systems (control of moving objects, jam-resistant radars, radioisotope measuring systems, electrical circuits with impulse sources), financial mathematics (description of stock price movements and valuation of stock options), mathematical biology and medicine (biomass control and drug delivery model) [2,3].
The goal of this paper is to develop the spectral method [4-6] for a problem of the probabilistic analysis for jump-diffusion systems. The spectral method formalism has been used previously to the stochastic systems with jumps generated by Poisson flow of events. Here we consider more complex problem which assumes that we have Erlang flow of jumps. This allows to investigate the stochastic systems with jumps in sample paths at the random time moments. Intervals between these moments can be described by not only the exponential distribution, but Erlang distribution [7].
2. Problem Statement
We assume that the system behavior is described by a jump-diffusion process. This process can be represented as a solution of the stochastic differential equation [1]:
 (1)
(1)
where 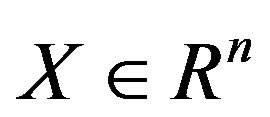 is a state vector,
is a state vector, 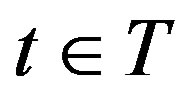 ,
,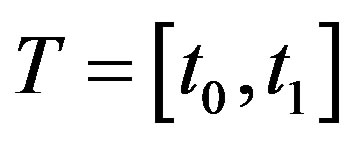 ;
;

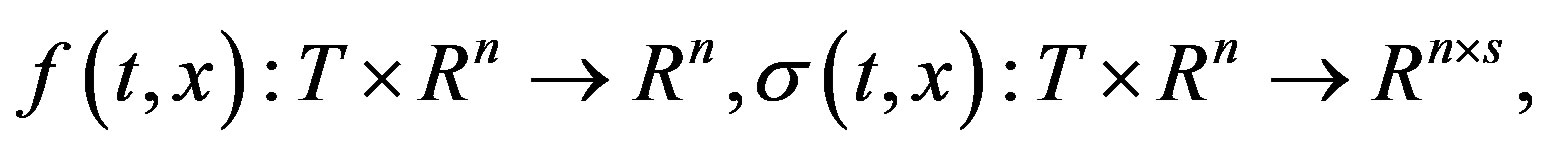 is an s-dimensional standard Wiener process independent of
is an s-dimensional standard Wiener process independent of .
.
The component 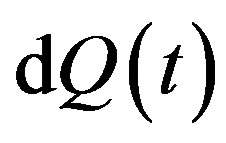 describes “extreme events” attended by jumps in sample paths of the process
describes “extreme events” attended by jumps in sample paths of the process  (e.g., a technical failure or a stock market crash). We assume that
(e.g., a technical failure or a stock market crash). We assume that

Here 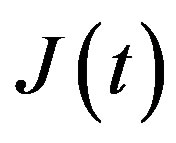 is the
is the 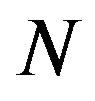 -th order Erlang process (Erlang process
-th order Erlang process (Erlang process 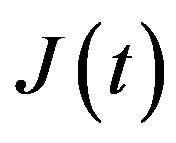 is a “censored” Poisson process in which
is a “censored” Poisson process in which 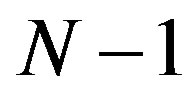 consecutive points are removed from a Poisson process
consecutive points are removed from a Poisson process  with the transition intensity
with the transition intensity 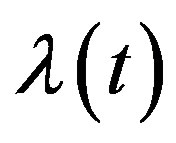 and then one point left unchanged [7]),
and then one point left unchanged [7]), 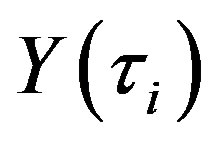 are independent random variables from
are independent random variables from 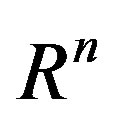 whose distribution is given by the probability density function
whose distribution is given by the probability density function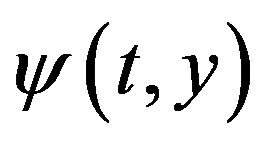 , i.e., state vector gets random increment at time moments
, i.e., state vector gets random increment at time moments 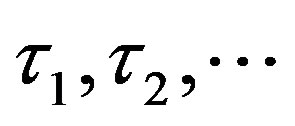 associated with Erlang flow of events [1]:
associated with Erlang flow of events [1]:

The process 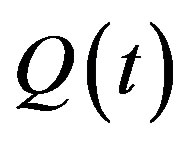 may be represented as
may be represented as
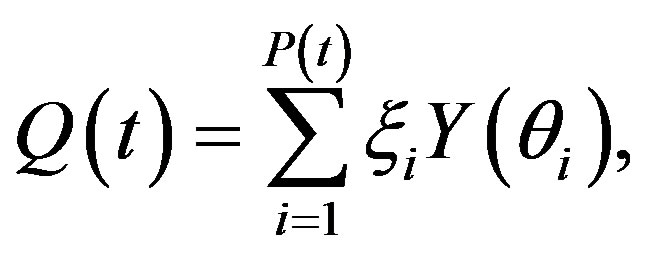
where the value  is used to “censor”
is used to “censor” 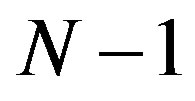 Poisson flow events in succession and to select each event which is a multiple of N (
Poisson flow events in succession and to select each event which is a multiple of N ( is the periodic function:
is the periodic function: ):
):
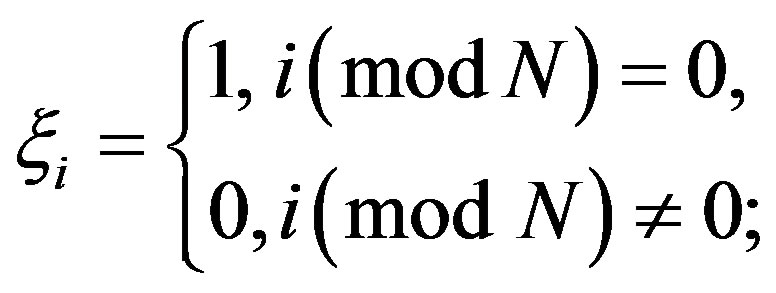
time moments 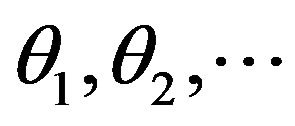 conform to the events in Poisson flow:
conform to the events in Poisson flow: .
.
Introduce a stochastic process 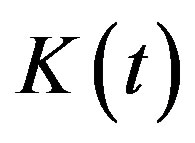 with a finite state set
with a finite state set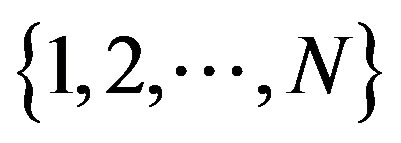 . These states are replaced sequentially starting from 1 with the transition intensity
. These states are replaced sequentially starting from 1 with the transition intensity :
:
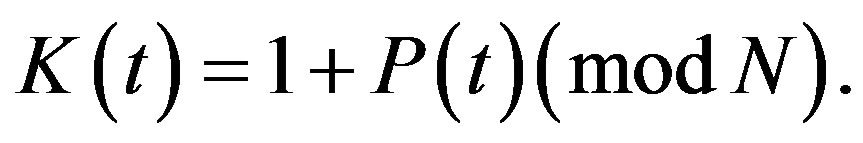
when the state with number  passes into the state with number 1, the state vector
passes into the state with number 1, the state vector  gets a random increment which leads to a jump in sample paths of the process
gets a random increment which leads to a jump in sample paths of the process  (see Figure 1).
(see Figure 1).
The introduction of the process  allows to represent the probability density function
allows to represent the probability density function  of the state vector
of the state vector  as follows:
as follows:

where functions  satisfy generalized Fokker-Planck equations [2,5,8]:
satisfy generalized Fokker-Planck equations [2,5,8]:
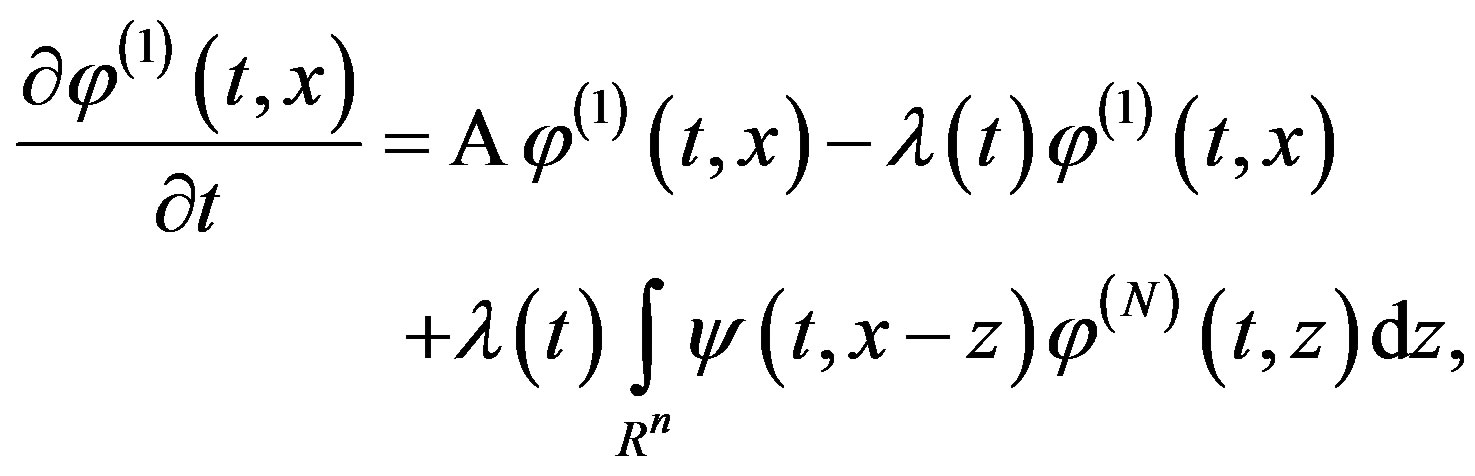 (2)
(2)

Figure 1. Sample paths of processes 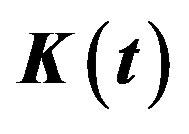 and
and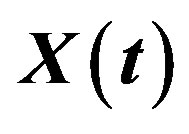 .
.
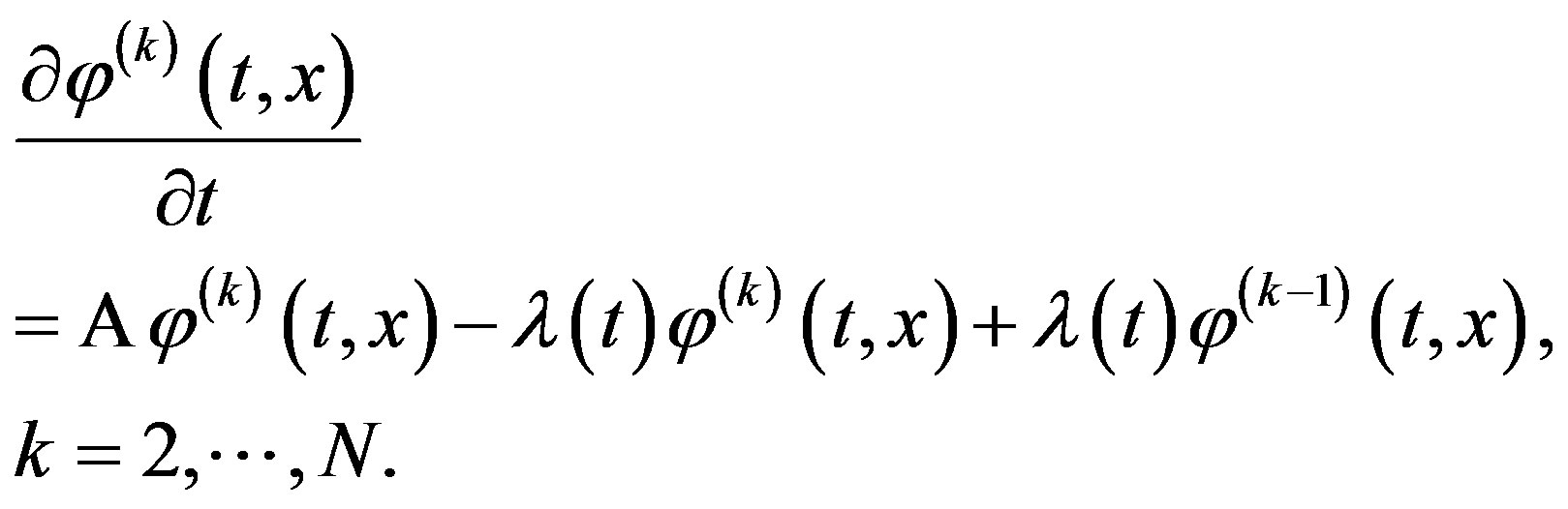 (3)
(3)
Here
 (4)
(4)
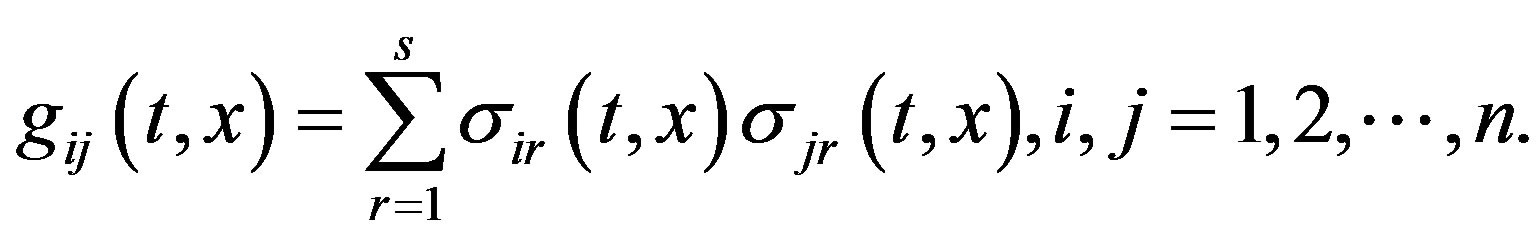
The initial state 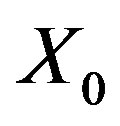 is determined by a given probability density function
is determined by a given probability density function . The initial state of the process
. The initial state of the process 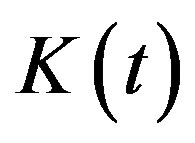 is fixed:
is fixed: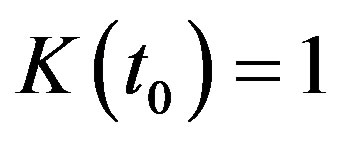 . So,
. So,
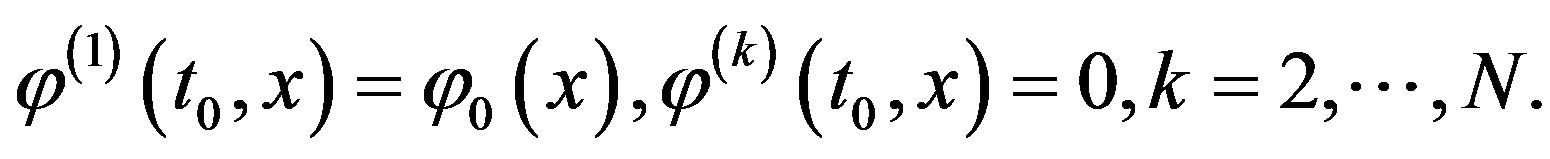 (5)
(5)
The last term on the right side of Equation (2) can be written in the operator form:
 (6)
(6)
for all admissible functions ;
;  is a linear operator which is a composition of the multiplication operator and the Fredholm operator with kernel
is a linear operator which is a composition of the multiplication operator and the Fredholm operator with kernel  .
.
The analysis problem of the stochastic systems with jumps described by Equation (1) is to find the probability density function  of the state vector
of the state vector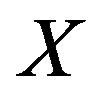 .
.
We assume that the unique solutions of Equation (1) and Equations (2)-(5) exist for given functions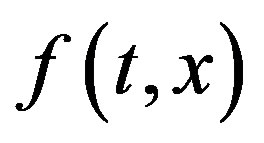 ,
, 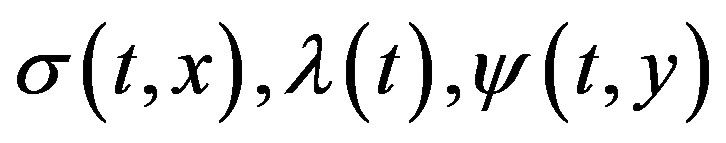 , and
, and .
.
3. Proposed Method: Overview of Spectral Method Formalism
Reduce the analysis problem to the finding of Fourier coefficients 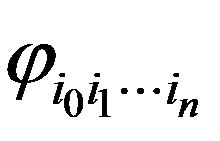 for the function
for the function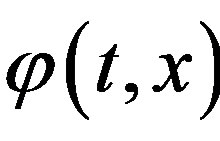 . Let
. Let
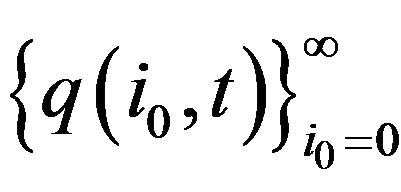 be an orthonormal basis of
be an orthonormal basis of 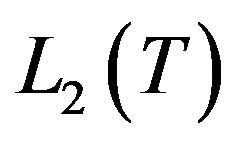 and let
and let 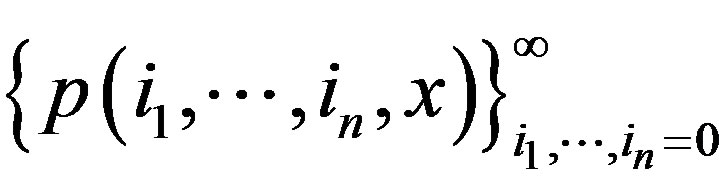 be an orthonormal basis of
be an orthonormal basis of 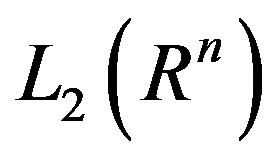 , then
, then  is the orthonormal basis of
is the orthonormal basis of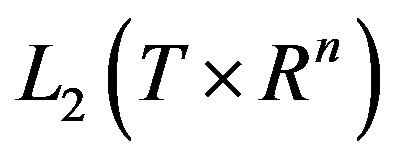 , where
, where

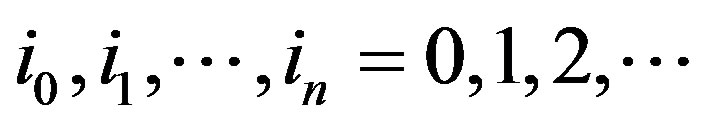 . So,
. So,

We apply the spectral method formalism [5,8] to Equation (2) and Equation (3) subject to the conditions (5), therefore
 (7)
(7)
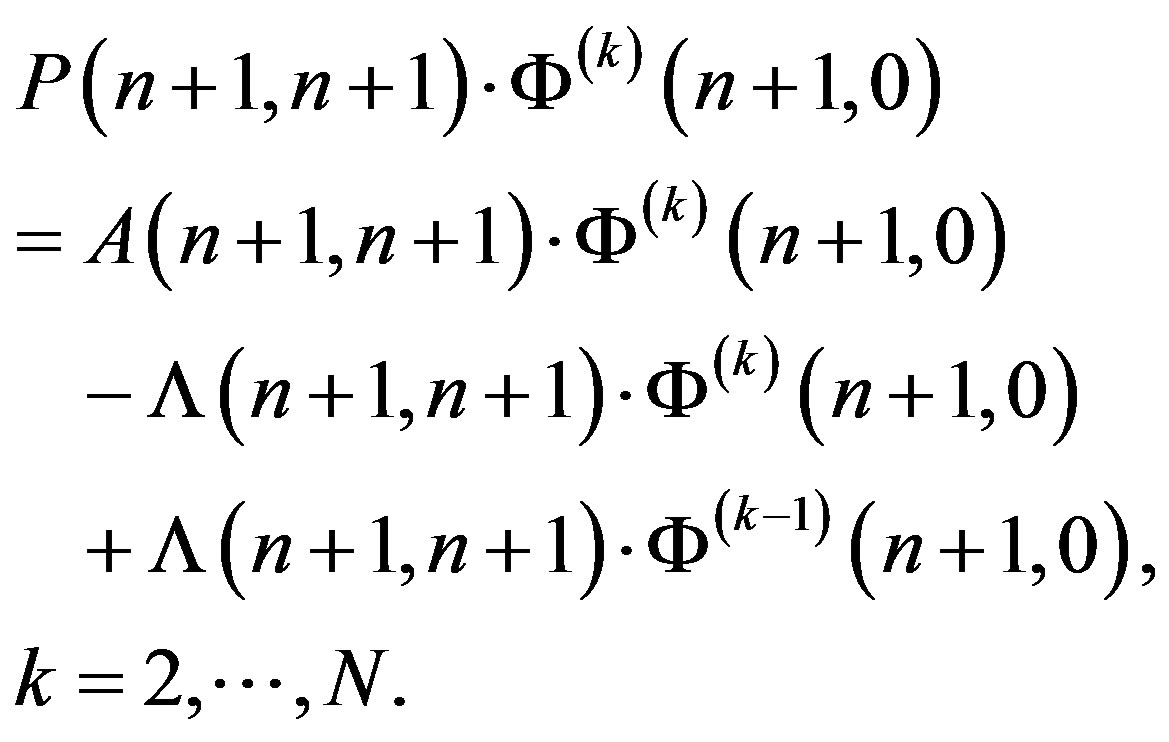 (8)
(8)
In these equations  is the spectral characteristic of the differential operator
is the spectral characteristic of the differential operator  subject to a function value at the initial time moment t0;
subject to a function value at the initial time moment t0; 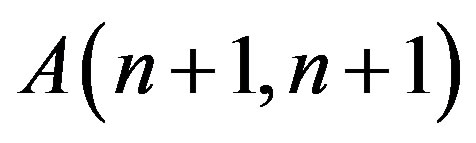 and
and 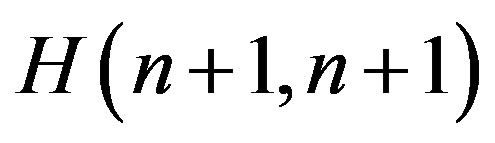 are the spectral characteristics of operators
are the spectral characteristics of operators  and
and  defined by (4)
defined by (4)
and (6), respectively, i.e.,  ,
,
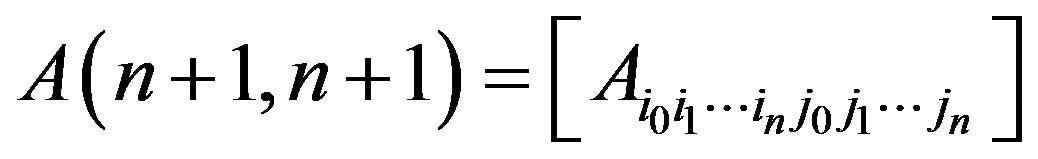 and
and

are 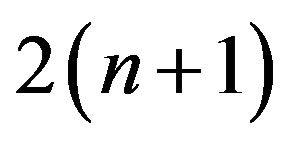 -dimensional matrices [9] (see Appendix) with elements
-dimensional matrices [9] (see Appendix) with elements
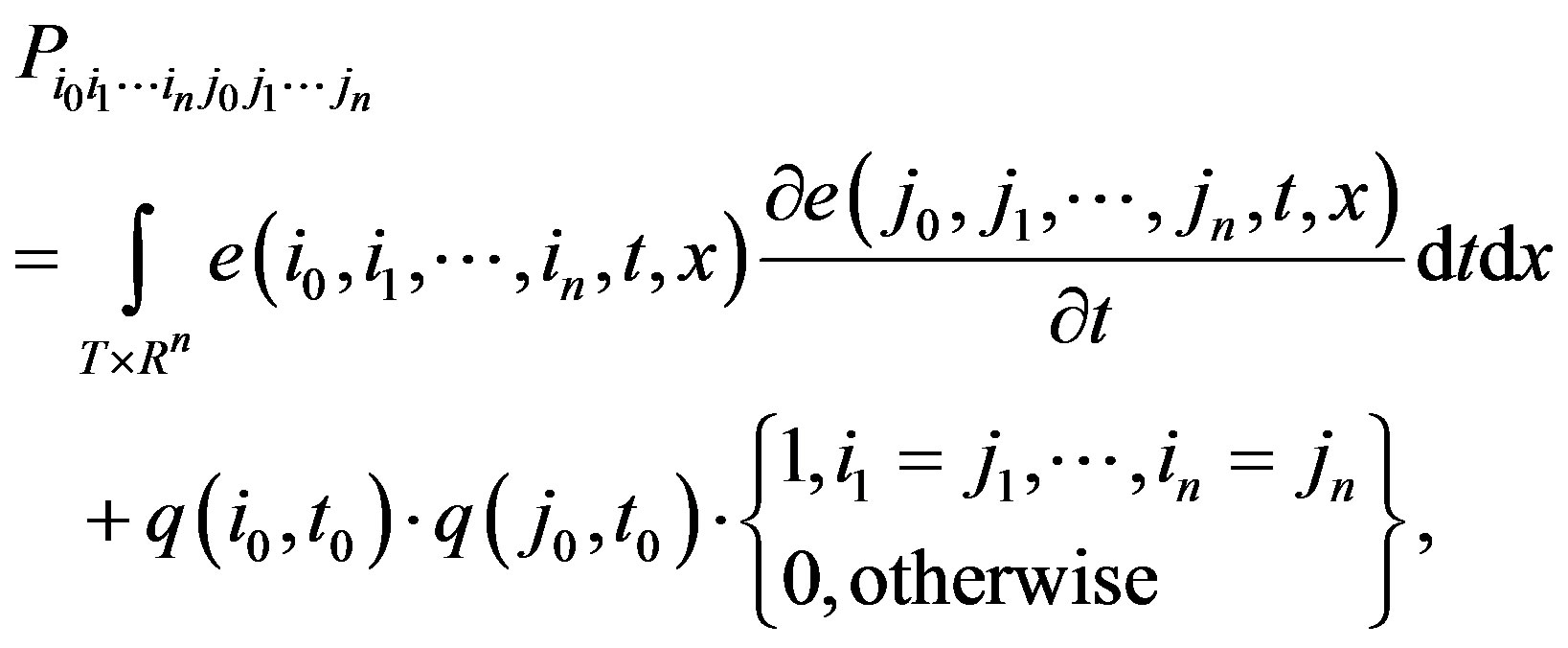

 is the spectral characteristic of the multiplication operator with multiplier
is the spectral characteristic of the multiplication operator with multiplier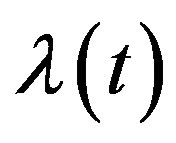 :
:
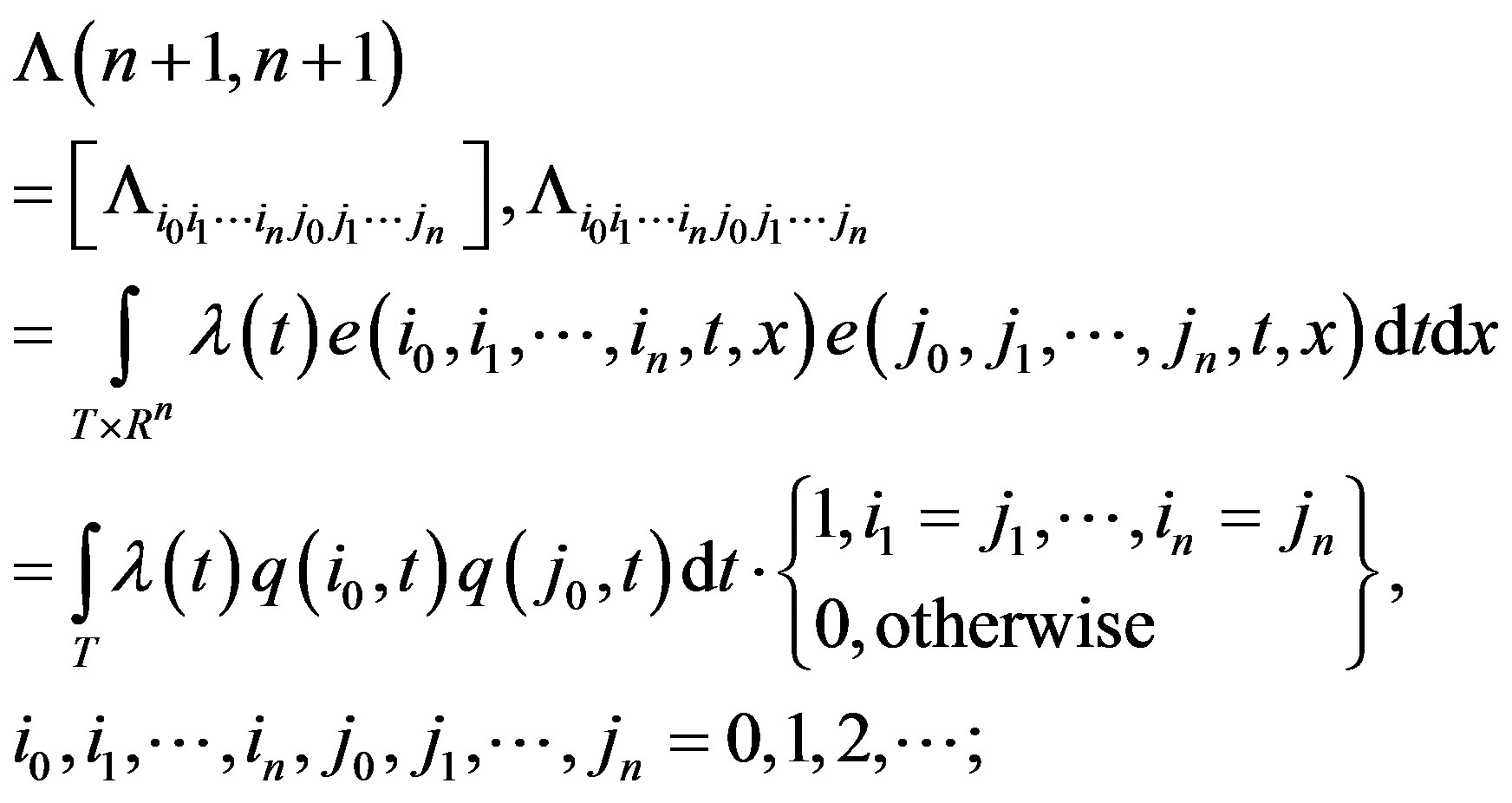
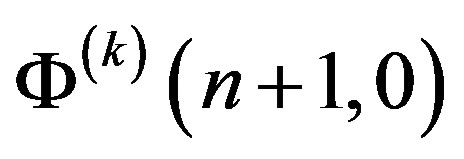 are the spectral characteristics of functions
are the spectral characteristics of functions . All these spectral characteristics are defined relative to
. All these spectral characteristics are defined relative to
 . Further, the
. Further, the 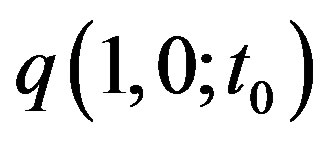 is the column matrix with values of functions
is the column matrix with values of functions  at the initial time moment
at the initial time moment :
:
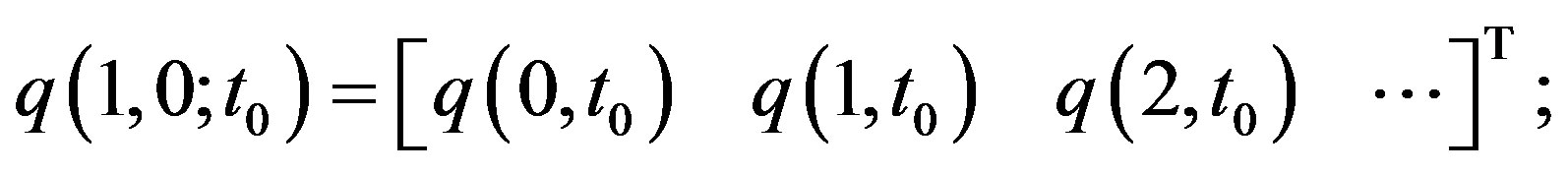
 is the spectral characteristic for the probability density function
is the spectral characteristic for the probability density function  of the initial state
of the initial state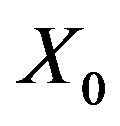 .
.
It is defined relative to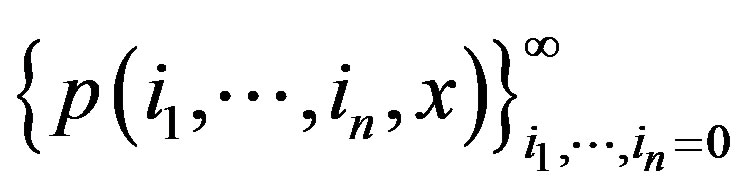 , i.e.,
, i.e.,

The spectral characteristic 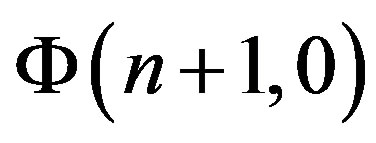 of the probability density function
of the probability density function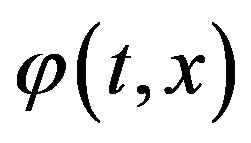 , also called a generalized characteristic function [5,6], may be expressed as follows (
, also called a generalized characteristic function [5,6], may be expressed as follows (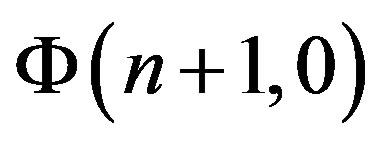 is the
is the  -multidimensional matrix formed by Fourier coefficients
-multidimensional matrix formed by Fourier coefficients ):
):
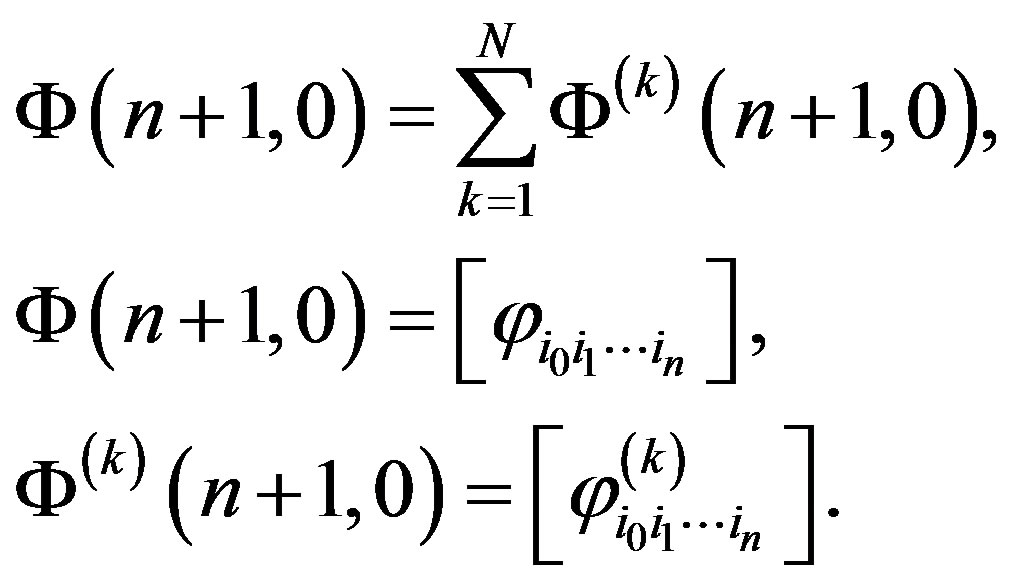 (9)
(9)
The properties of the spectral characteristics for functions and linear operators in Equations (7)-(9) are described in [5,8].
As a rule [5,6], the spectral characteristic  is expressed in terms of the spectral characteristics for differential operators and multiplication operators:
is expressed in terms of the spectral characteristics for differential operators and multiplication operators:

where  and
and 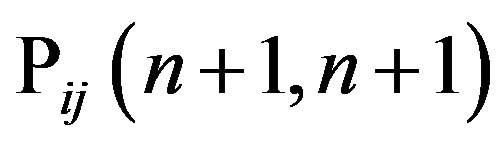 are the spectral characteristics of first-order and second-order differential operators
are the spectral characteristics of first-order and second-order differential operators  and
and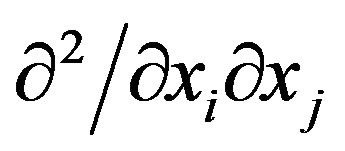 , respectively;
, respectively; 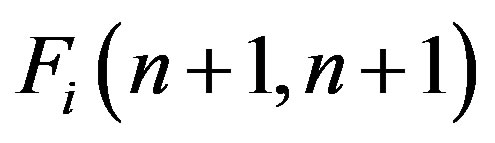 and
and 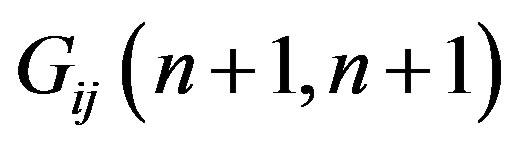 are the spectral characteristics of multiplication operators with multipliers
are the spectral characteristics of multiplication operators with multipliers 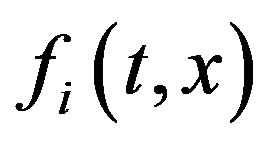 and
and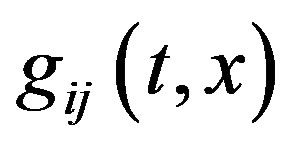 , respectively. These spectral characteristics are defined like a
, respectively. These spectral characteristics are defined like a 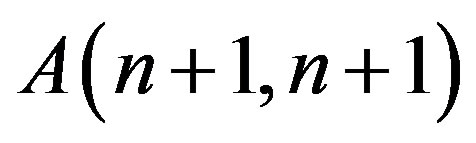 relative to the orthonormal basis
relative to the orthonormal basis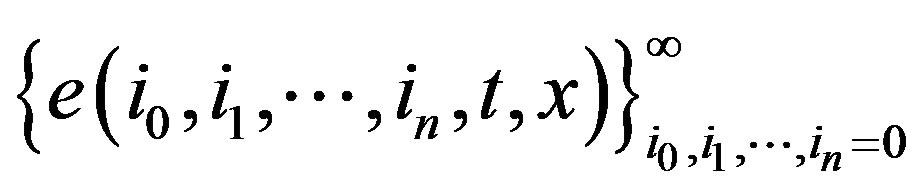 .
.
Such definition of 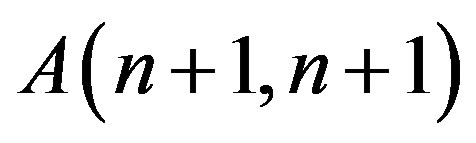 is more preferred since there are analytical expressions of the spectral characteristics relative to various orthonormal functions for differential operators and multiplication operators (see [4,5]).
is more preferred since there are analytical expressions of the spectral characteristics relative to various orthonormal functions for differential operators and multiplication operators (see [4,5]).
Equation (7) and Equation (8) are linear matrix equations for the spectral characteristics  or linear algebraic equations for Fourier coefficients
or linear algebraic equations for Fourier coefficients 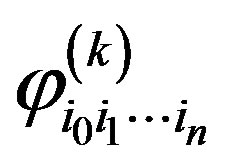
(for functions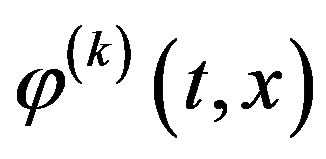 ). Let us consider the solution of these equations.
). Let us consider the solution of these equations.
It follows from Equation (8) that
 (10)
(10)
i.e.,

or
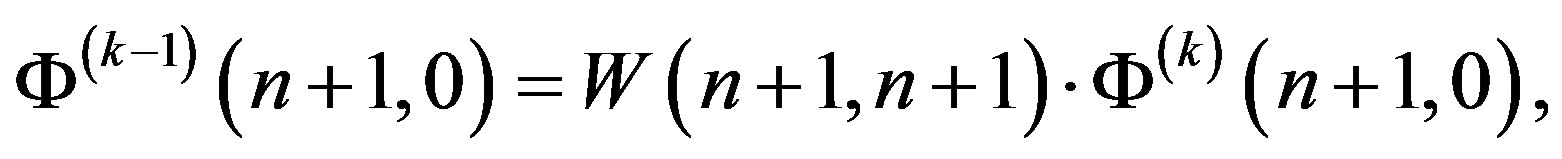
where
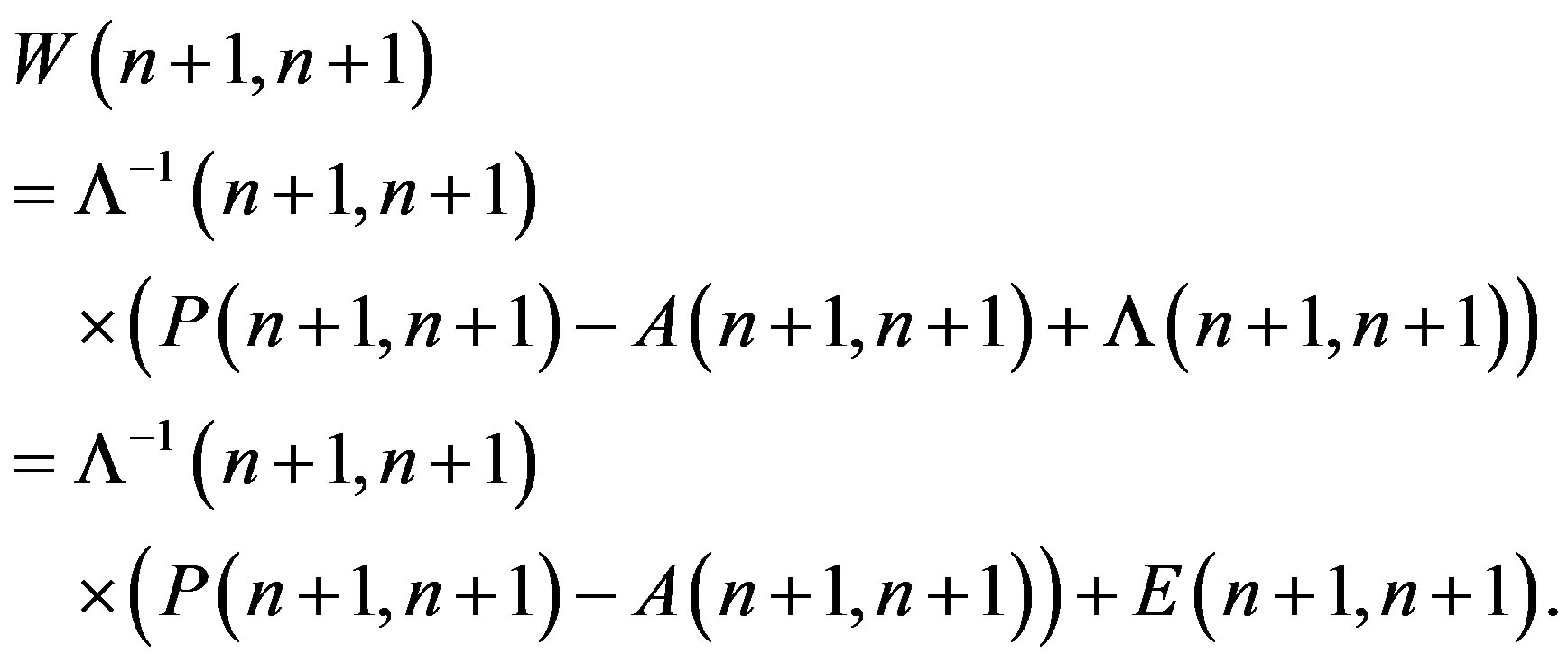
Thus,

in particular
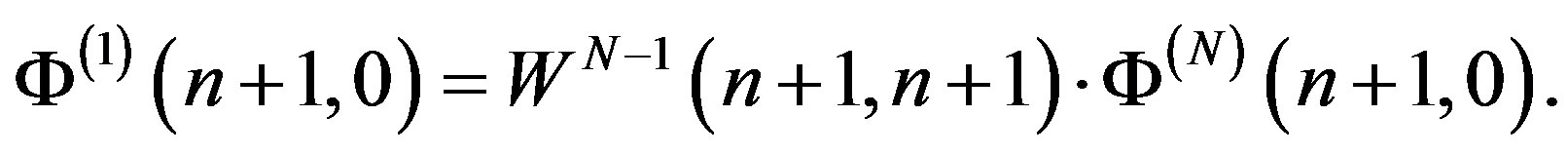 (11)
(11)
We rewrite Equation (7) subject to Equation (11):

or
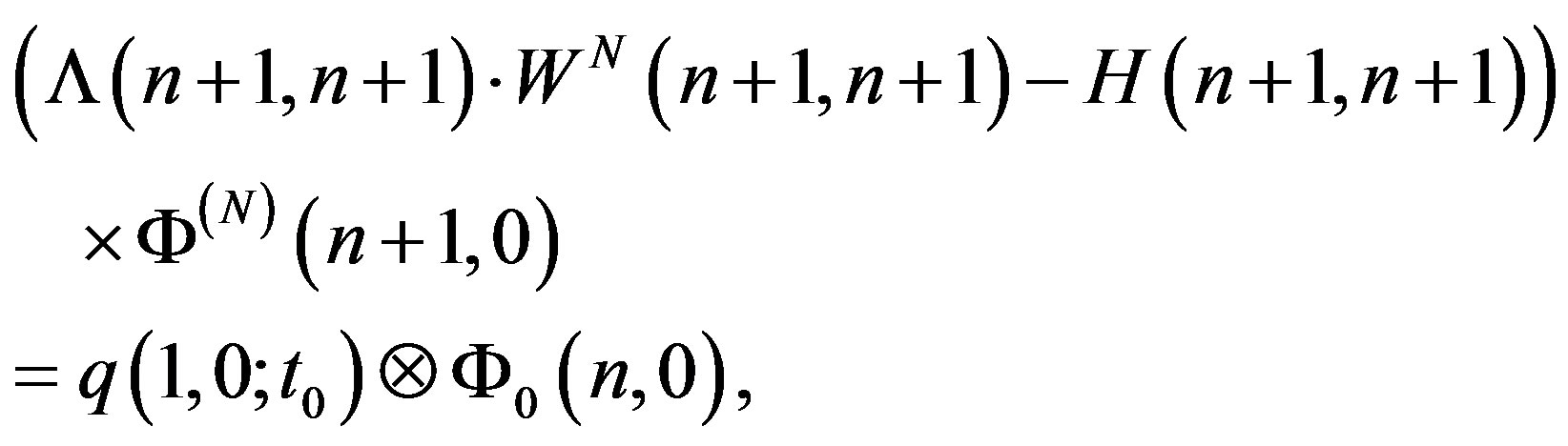
therefore

We express the spectral characteristic 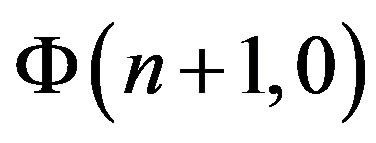 subject to Equation (9):
subject to Equation (9):
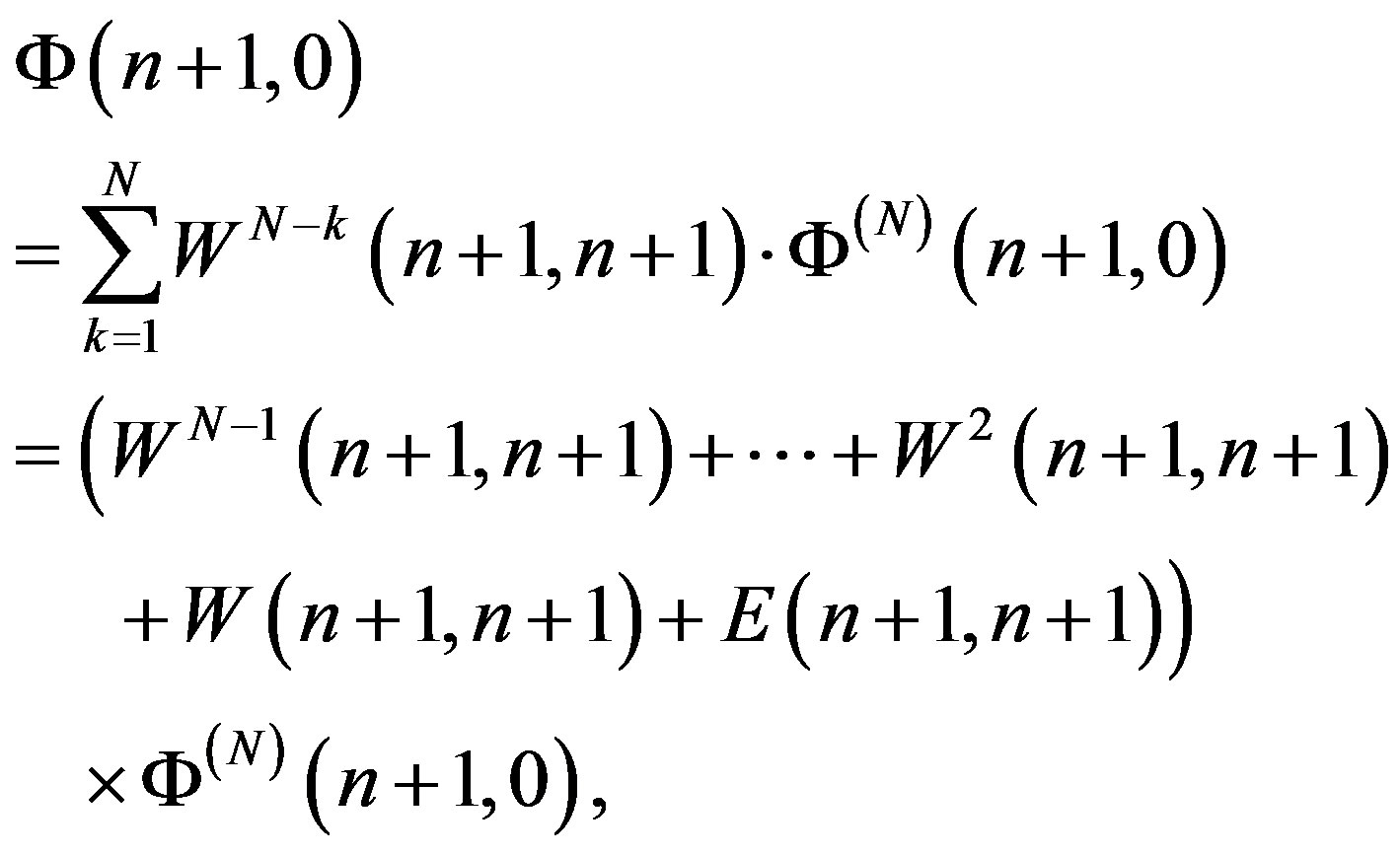
where  is the
is the 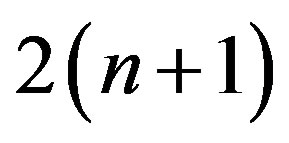 -dimensional identity matrix. The expression in parentheses is multiplied on the right by the difference
-dimensional identity matrix. The expression in parentheses is multiplied on the right by the difference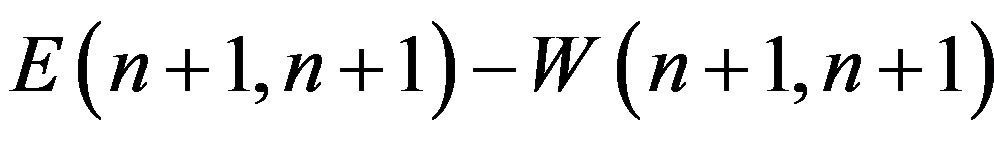 :
:

i.e.,
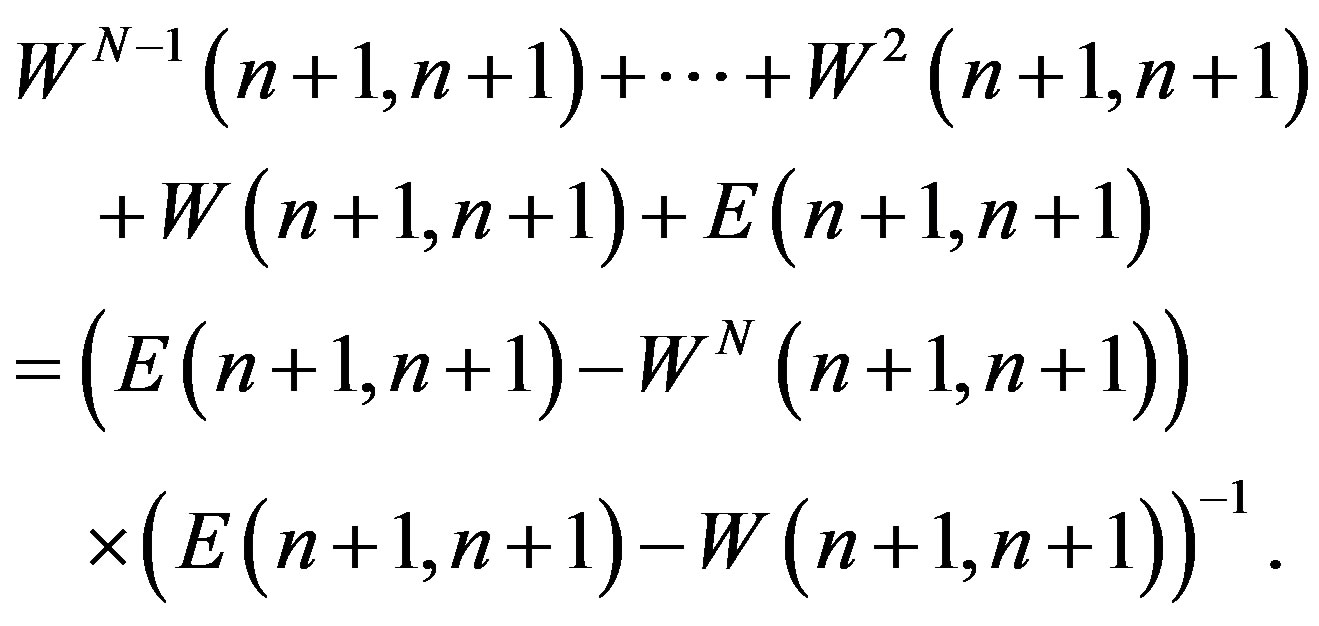 (12)
(12)
A similar result can be obtained by multiplying on the left by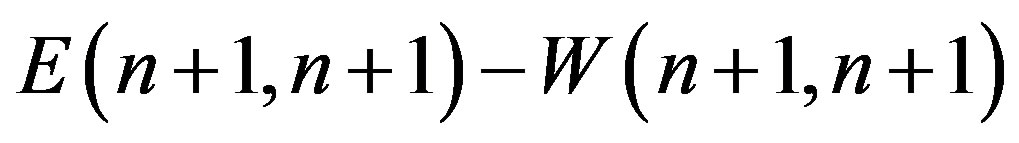 :
:
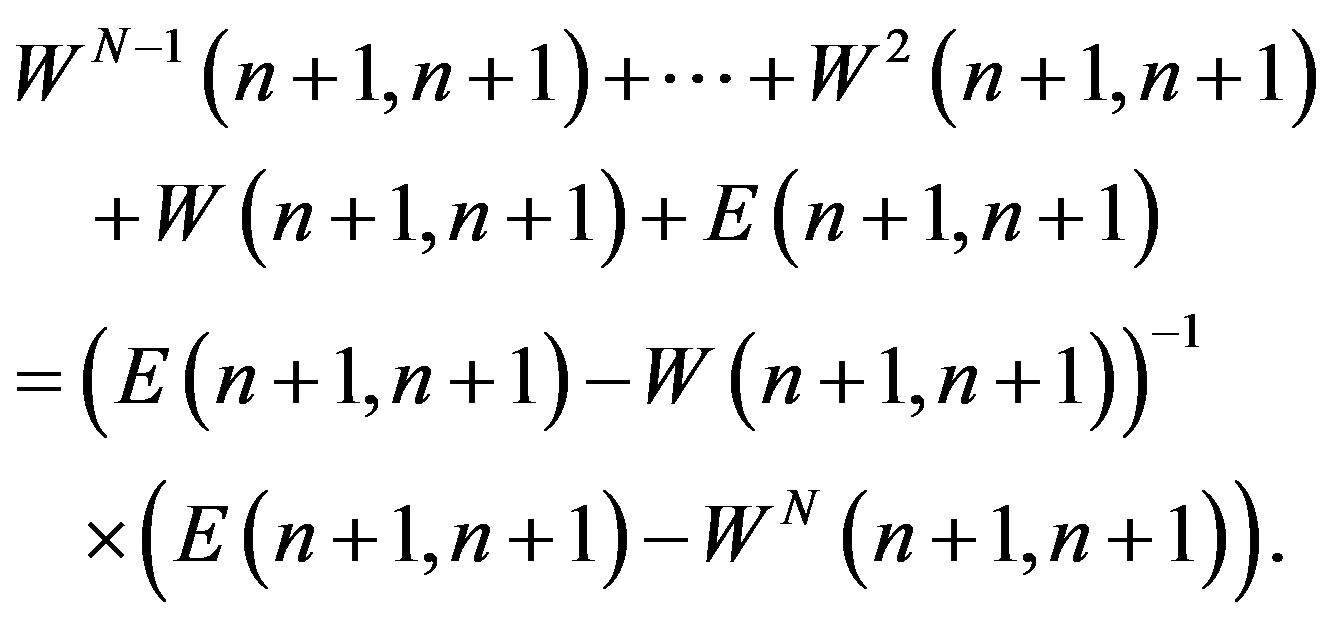 (13)
(13)
Equations (12) and (13), obviously, are analogues of geometric series sum. Thus,
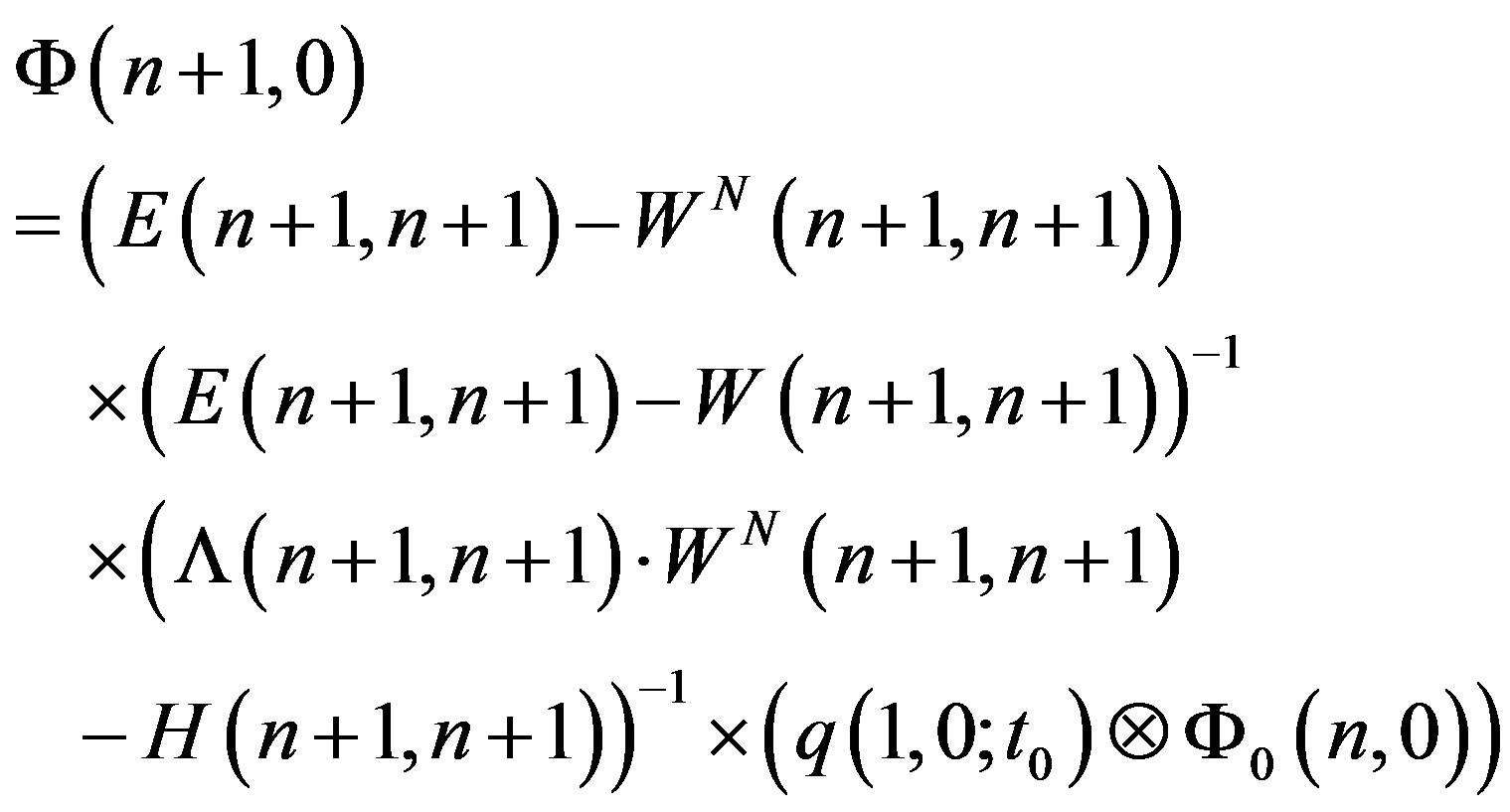 (14)
(14)
or
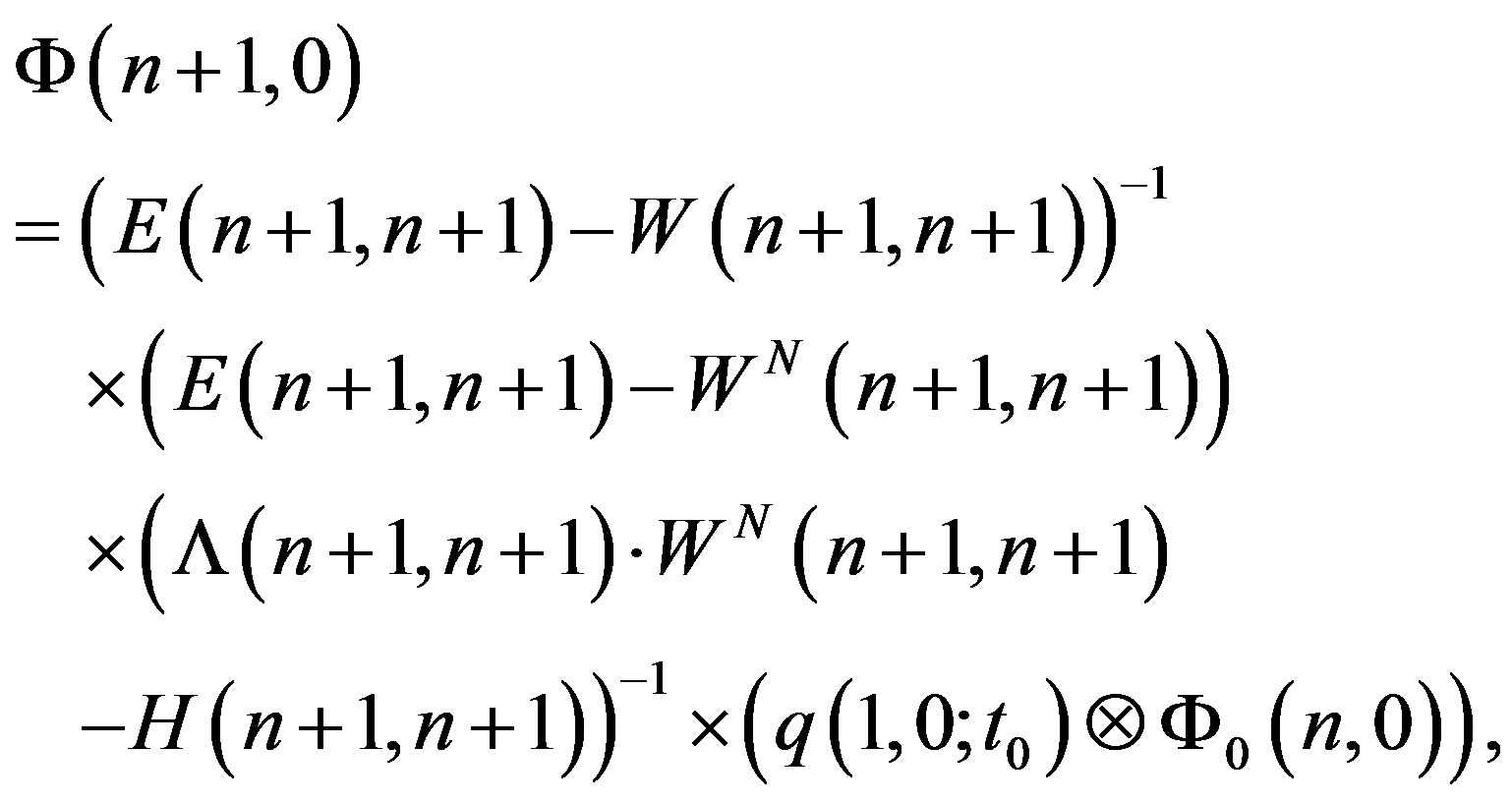 (15)
(15)
are the problem solutions by the spectral method formalism.
It is easy to see that if  (order of Erlang process) the problem reduces to the analysis of the stochastic systems with Poisson flow of jumps and
(order of Erlang process) the problem reduces to the analysis of the stochastic systems with Poisson flow of jumps and

when jump part is missed:

we obtain the known solution of analysis problem for the stochastic systems with continuous trajectories [5,6]:

It is required to apply the inversion formula for finding the solution of the analysis problem [5]:
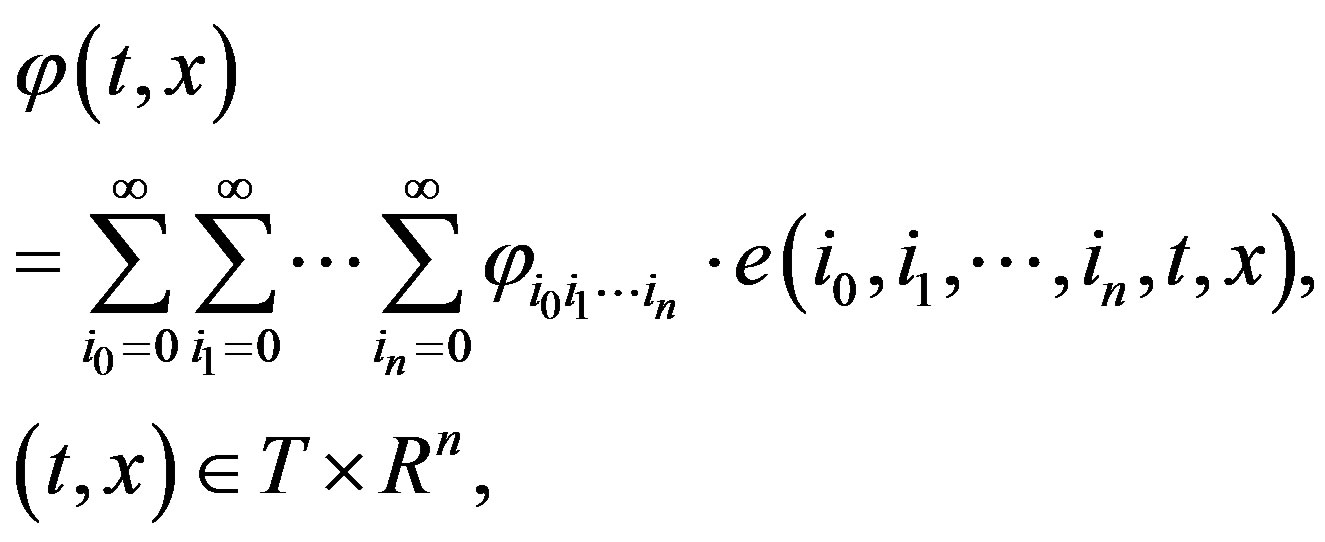
but a finite number of coefficients 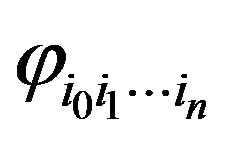 is usually defined approximately since the problem of finding all Fourier coefficients is not trivial. In this case, the infinite matrices in Equations (7)-(9) are replaced by truncated matrices. Then
is usually defined approximately since the problem of finding all Fourier coefficients is not trivial. In this case, the infinite matrices in Equations (7)-(9) are replaced by truncated matrices. Then

where natural numbers  are the selected orders of the truncation for the spectral characteristics.
are the selected orders of the truncation for the spectral characteristics.
Remarks
1) The solution of the analysis problem is possible to find in another way. To do this we express  in terms of
in terms of  from Equation (10), then we express
from Equation (10), then we express 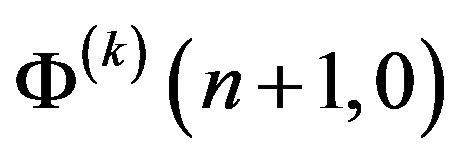 in terms of
in terms of
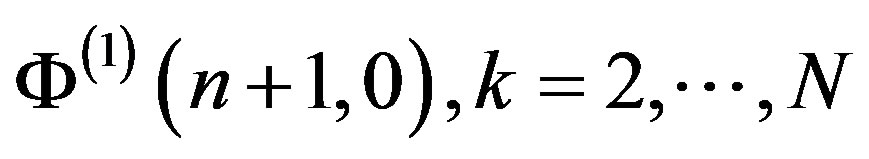 , that makes it possible to express
, that makes it possible to express 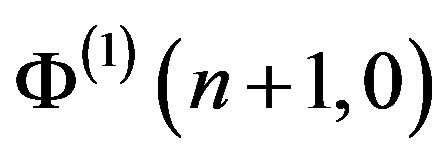 from the Equation (7). The next step is to develop the final formula for
from the Equation (7). The next step is to develop the final formula for 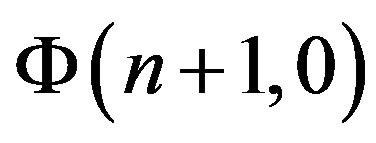 subject to Equation (9) and the similar transformations carried out to express Equations (14) and (15):
subject to Equation (9) and the similar transformations carried out to express Equations (14) and (15):
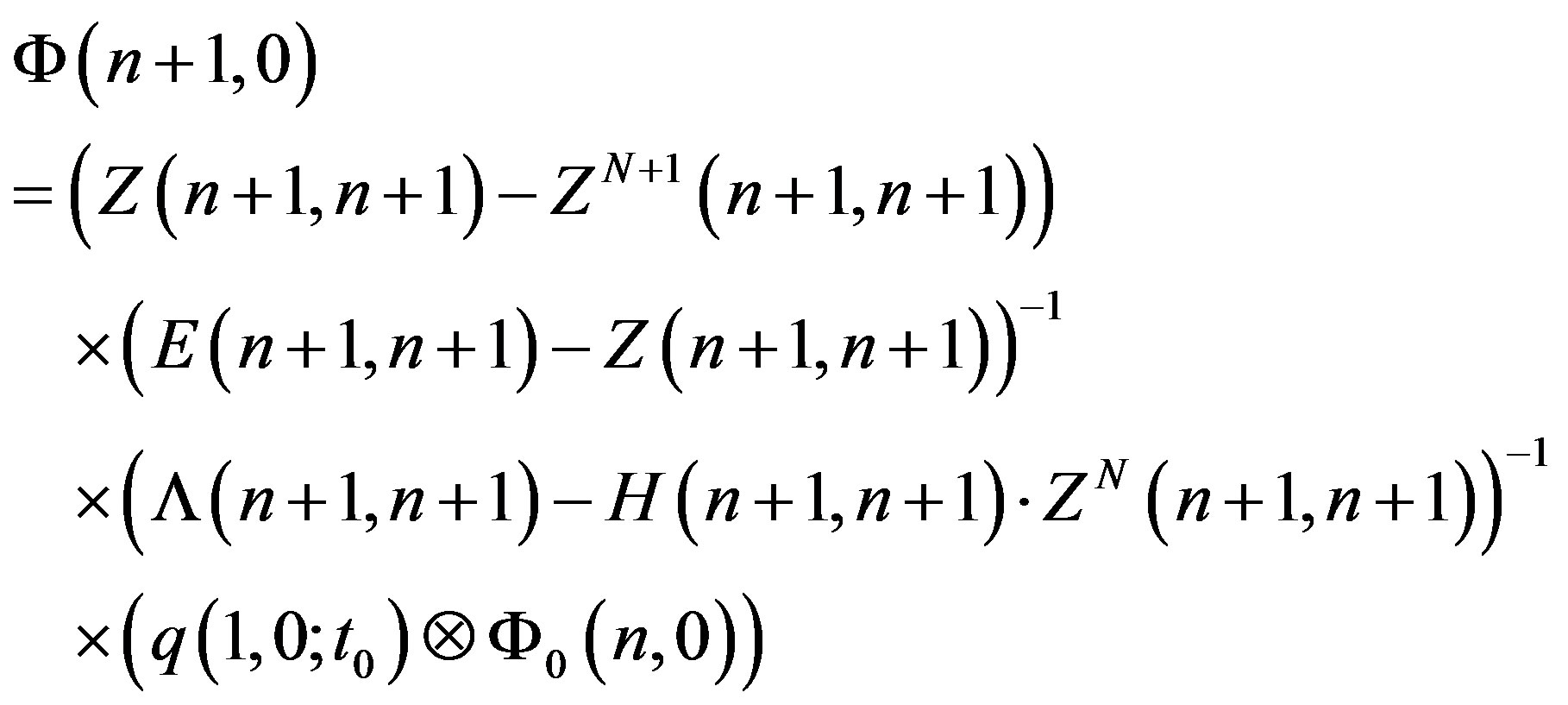
or
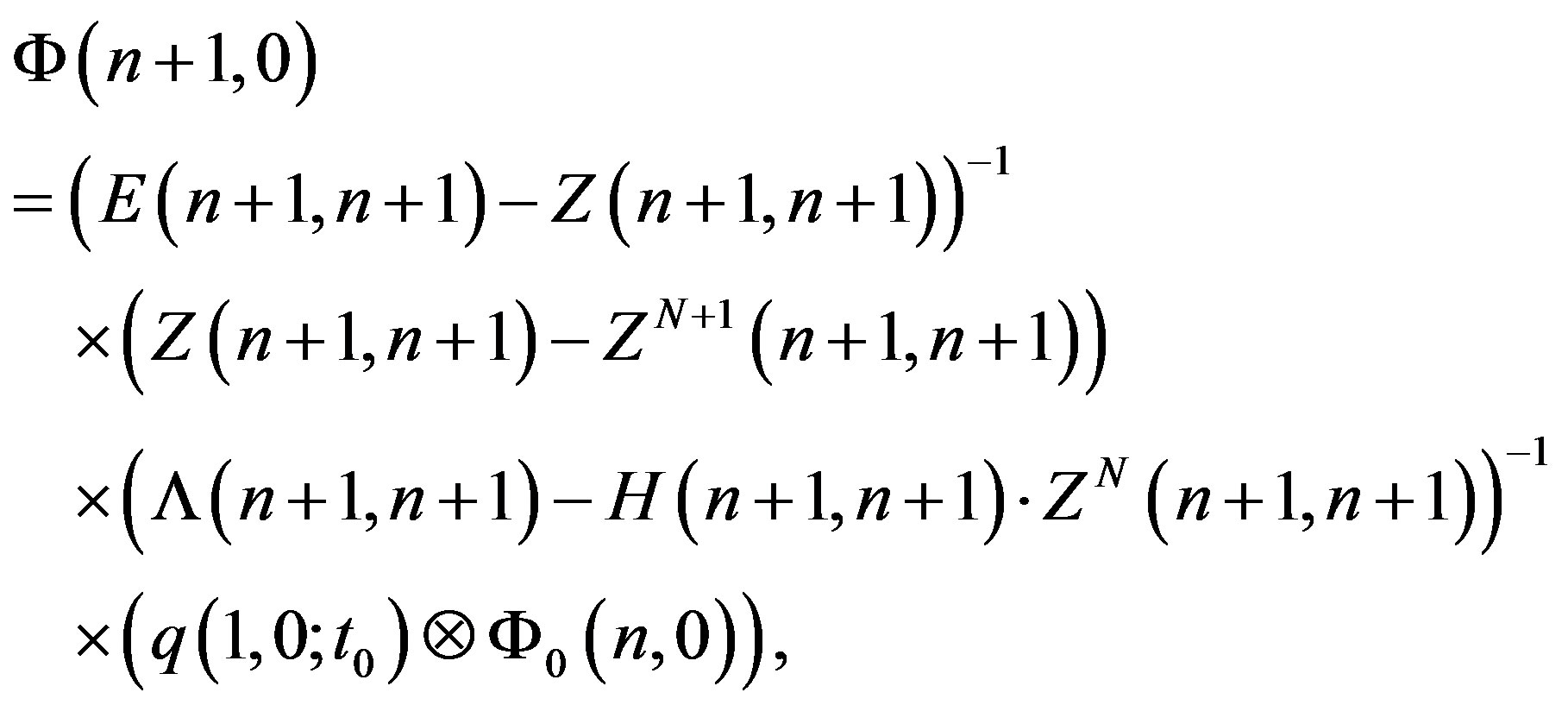
where

These expressions are equivalent to Equations (14) and (15), but Equations (14) and (15) are preferable since finding the inverse spectral characteristic 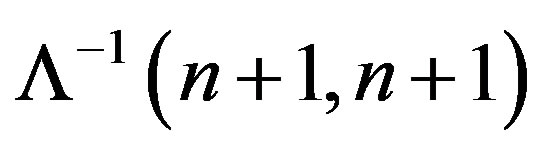 can be avoided in this case by defining
can be avoided in this case by defining  as the spectral characteristic of the multiplication operator with multiplier
as the spectral characteristic of the multiplication operator with multiplier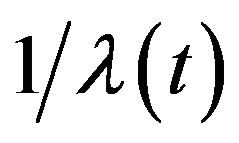 . In particular, when the transition intensity is constant
. In particular, when the transition intensity is constant  we have
we have

2) A generalization of the discussed problem is to consider the transition intensity which depends on the state vector. The jump size may be described by the conditional probability density function 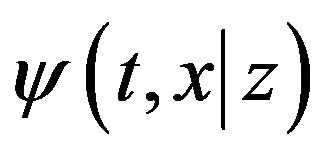 that characterizes the distribution of the state vector
that characterizes the distribution of the state vector 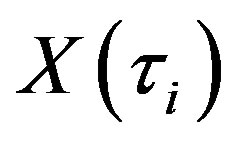 after the jump. This distribution depends on the previous value
after the jump. This distribution depends on the previous value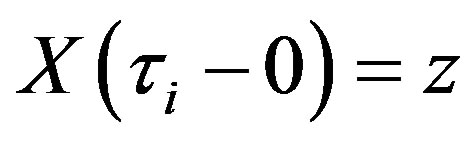 ; jumps in sample paths of the process
; jumps in sample paths of the process  occur at time moment
occur at time moment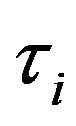 .
.
In this case Equations (2) and (3) are represented as
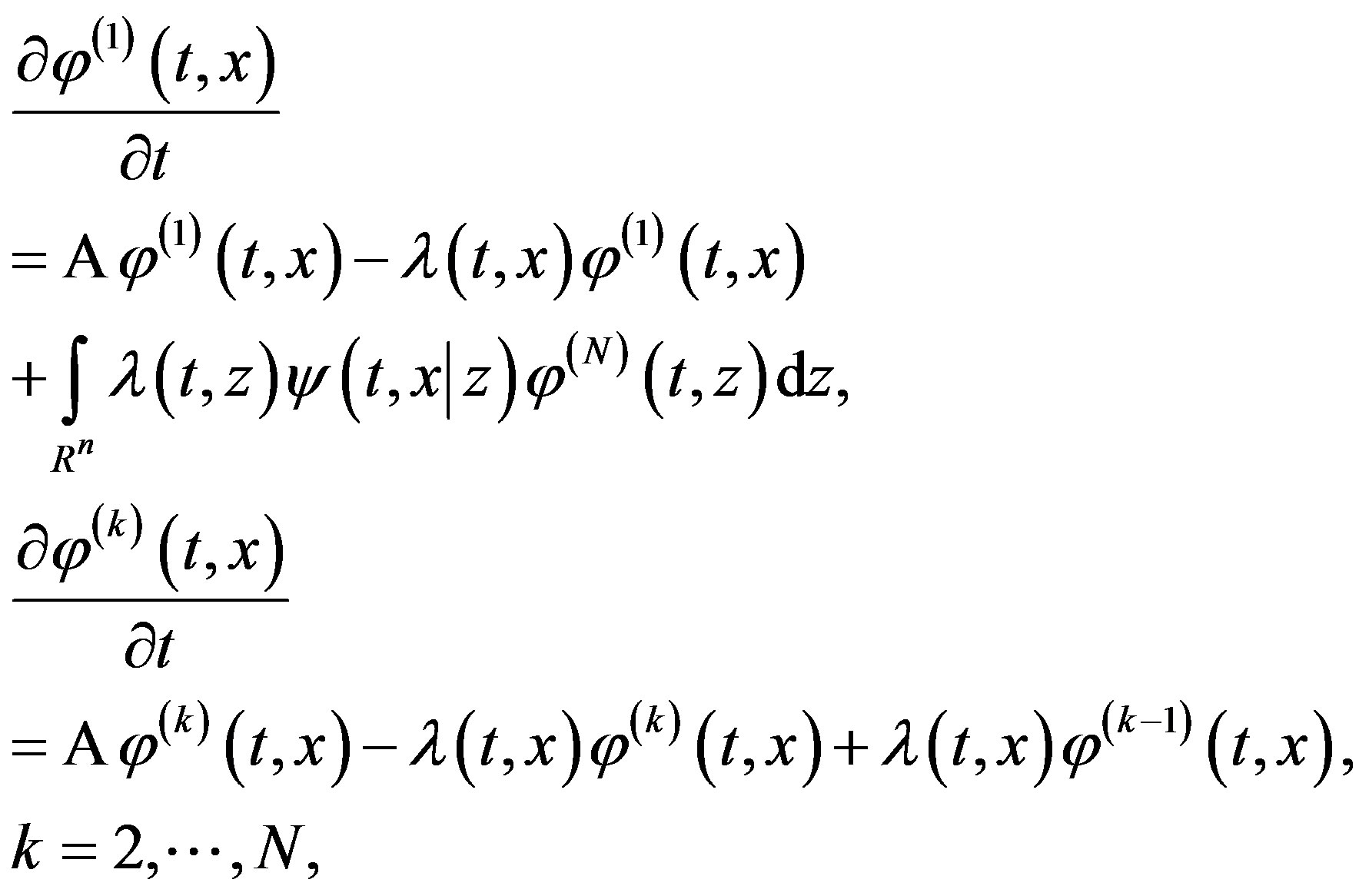
and the operator  (see Equation (6)) must be redefined as
(see Equation (6)) must be redefined as
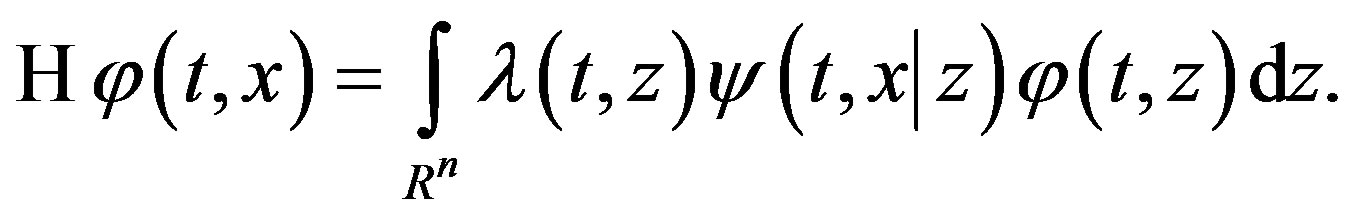
Equations (7) and (8) will not change (but 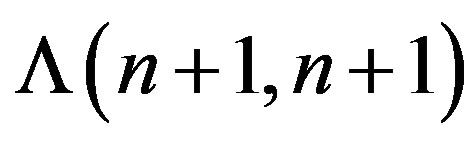 is the spectral characteristic of the multiplication operator with multiplier
is the spectral characteristic of the multiplication operator with multiplier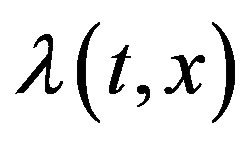 , the spectral characteristic
, the spectral characteristic 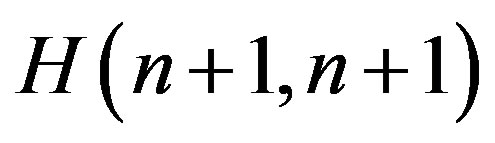 is calculated according to a new definition of the operator
is calculated according to a new definition of the operator ). Therefore methods for the problem solution will not change as well as Equations (14) and (15).
). Therefore methods for the problem solution will not change as well as Equations (14) and (15).
4. Conclusions
We examine using of the spectral method formalism to the probabilistic analysis problem for the stochastic systems with jumps generated by Erlang flow of events. Finding of the probability density function for the state vector by the spectral method formalism are developed.
Using of Erlang flow of events allows to consider a more complex behavior for sample paths of the process . The occurrence of jumps in sample paths can be controlled by appropriate selection of parameters such as the transition intensity
. The occurrence of jumps in sample paths can be controlled by appropriate selection of parameters such as the transition intensity  and an order
and an order  (for Erlang process). This option makes it quite flexible tool for modeling. Thus, for
(for Erlang process). This option makes it quite flexible tool for modeling. Thus, for  time intervals between jumps are described by exponential distribution law, for
time intervals between jumps are described by exponential distribution law, for 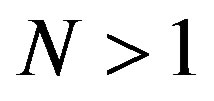 time intervals between jumps are described by Erlang distribution, which is a special case of the gamma distribution. Erlang distribution converges to the normal distribution as
time intervals between jumps are described by Erlang distribution, which is a special case of the gamma distribution. Erlang distribution converges to the normal distribution as  increases.
increases.
The application of the spectral method formalism allows to reduce integro-differential equations to linear algebraic equations for Fourier coefficients of the probability density function. It essentially simplifies the solution.
5. Acknowledgements
This work is supported by RFBR grant 12-08-00892-а.
REFERENCES
- V. S. Pugachev and I. N. Sinitsyn, “Stochastic Systems: Theory and Applications,” World Scientific, New Jersey, 2001.
- I. E. Kazakov, V. M. Artem’ev and V. A. Bukhalev, “Analysis of Systems with Random Structure,” Fizmatlit, Moscow, 1993. (In Russian: И. Е. Казаков, В. М. Артемьев, В. А. Бухалев, “Анализ систем случайной стру- ктуры,” Физматлит, Москва, 1993.)
- F. B. Hanson, “Applied Stochastic Processes and Control for Jump-Diffusions,” SIAM, Philadelphia, 2007.
- V. V. Solodovnikov, V. V. Semenov, M. Peschel and D. Nedo, “Design of Control Systems on Digital Computers: Spectral and Interpolational Methods,” Verlag Technik, Berlin; Maschinostrojenije, Moscow, 1979. (In German: W. W. Solodownikow, W. W. Semjonow, M. Peschel and D. Nedo, “Berechnung von Regelsystemen auf Digitalrechnern: Anwendung von Spektral und Interpolationsmethoden,” Verlag Technik, Berlin, 1979; In Russian: В. В. Солодовников, В. В. Семенов, М. Пешель, Д. Недо, “Расчет систем управления на ЦВМ: спектральный и интерполяционный методы,” Машиностроение, Мо- сква, 1979.)
- A. V. Panteleev, K. A. Rybakov and I. L. Sotskova, “Spectral Method of Nonlinear Stochastic Control System Analysis,” Vuzovskaya kniga, Moscow, 2006. (In Russian: А. В. Пантелеев, К. А. Рыбаков, И. Л. Сотскова, “Спектральный метод анализа нелинейных стохаст- ических систем управления,” Вузовская книга, Моск- ва, 2006.)
- A. V. Panteleev and K. A. Rybakov, “Analyzing Nonlinear Stochastic Control Systems in the Class of Generalized Characteristic Functions,” Automation and Remote Control, Vol. 72, No. 2, 2011, pp. 393-404. doi:10.1134/S0005117911020159
- F. A. Haight, “Handbook of the Poisson Distribution,” John Wiley & Sons, New York, 1967.
- K. A. Rybakov and I. L. Sotskova, “Spectral Method for Analysis of Switching Diffusions,” IEEE Transactions on Automatic Control, Vol. 52, No. 7, 2007, pp. 1320-1325. doi:10.1109/TAC.2007.900841
- M. Lindner, “Infinite Matrices and their Finite Sections: An Introduction to the Limit Operator Method,” Birkhäuser, Basel, 2006.
Appendix
Multidimensional Matrix Operations
1) Let  and let
and let 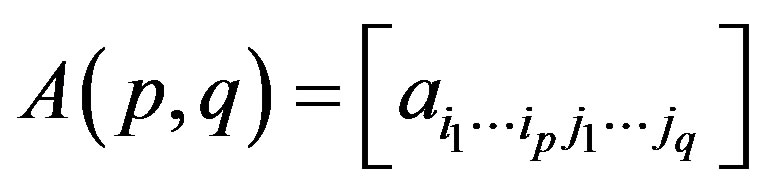 and
and 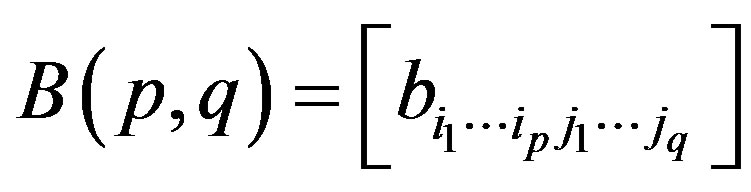 be the infinite
be the infinite 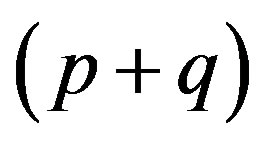 -dimensional matrices. The expression
-dimensional matrices. The expression 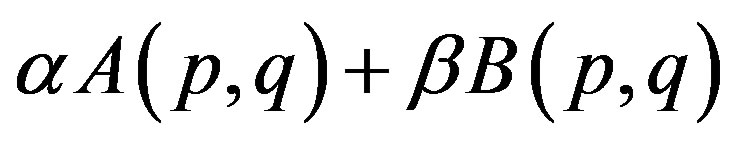
is the infinite  -dimensional matrix
-dimensional matrix
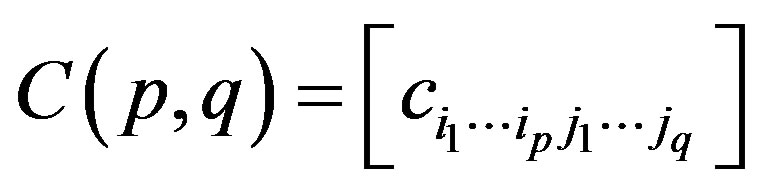 if
if
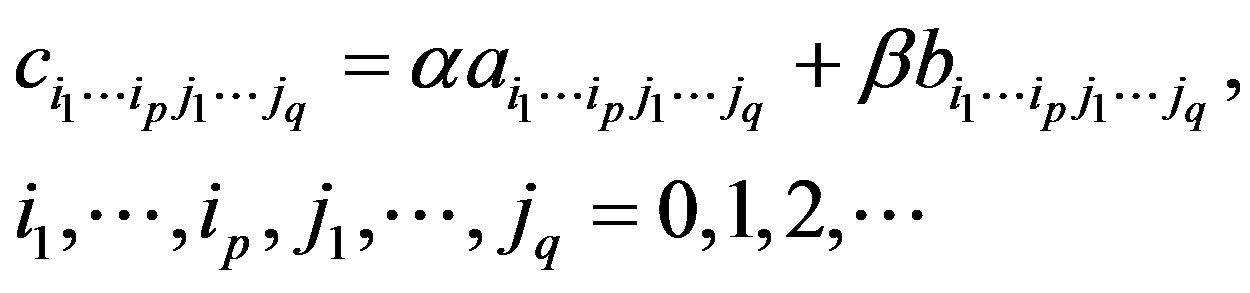
2) Let  and
and 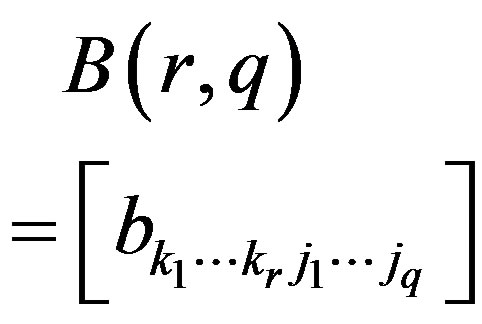 be the infinite
be the infinite  -dimensional and
-dimensional and 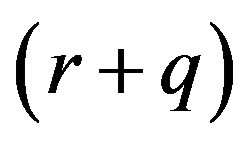 -dimensional matrices, respectively. The product
-dimensional matrices, respectively. The product  is the infinite
is the infinite 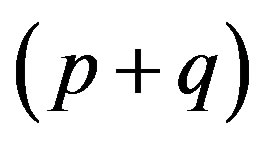 -dimensional matrix
-dimensional matrix 
if
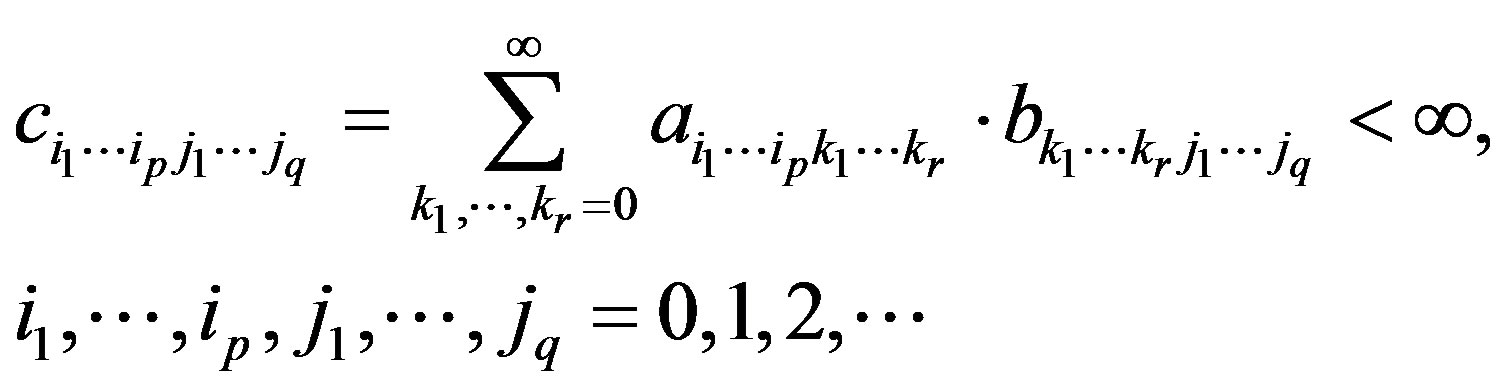
An infinite  -dimensional matrix
-dimensional matrix 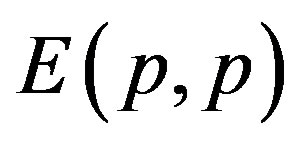 is said to be the identity matrix if
is said to be the identity matrix if

for each 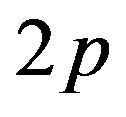 -dimensional matrix
-dimensional matrix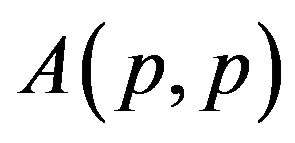 . We use the notation
. We use the notation 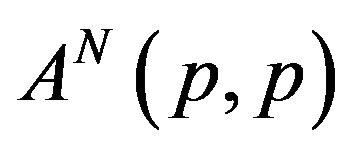 to denote the product
to denote the product

3) Let  be an infinite
be an infinite  -dimensional matrix. An infinite
-dimensional matrix. An infinite  -dimensional matrix
-dimensional matrix  is said to be the two-sided inverse of
is said to be the two-sided inverse of  if
if
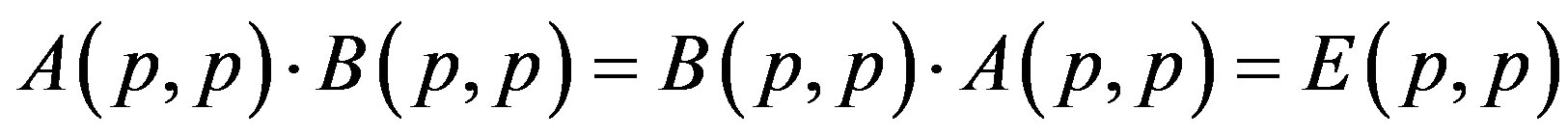 .
.
We use the notation 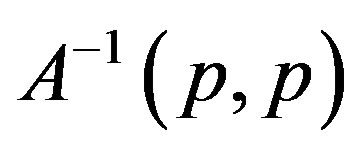 to denote the twosided inverse of
to denote the twosided inverse of .
.
4) Let 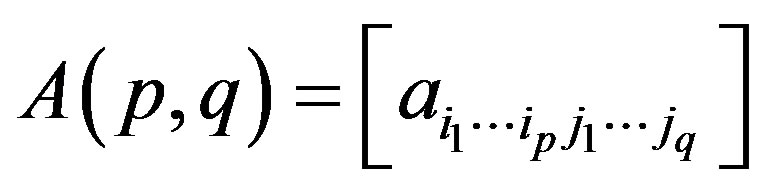 and
and 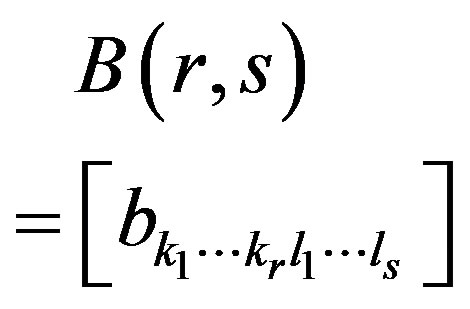 be the infinite
be the infinite 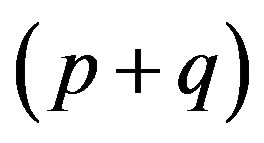 -dimensional and
-dimensional and  -dimensional matrices, respectively. The tensor product
-dimensional matrices, respectively. The tensor product  is the infinite
is the infinite 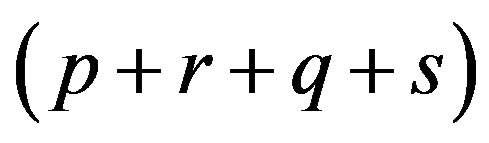 -dimensional matrix
-dimensional matrix 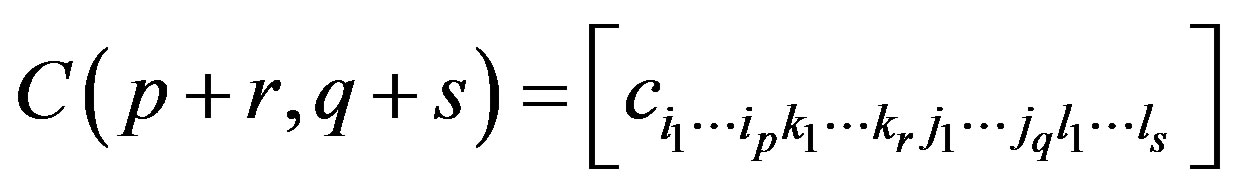 if
if

5) Let  be an infinite
be an infinite 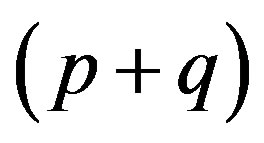
-dimensional matrix. An infinite 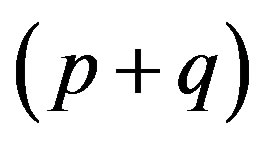 -dimensional matrix
-dimensional matrix  is said to be the transpose of
is said to be the transpose of 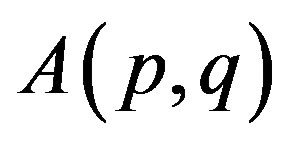 if
if

We use the notation  to denote the transpose of
to denote the transpose of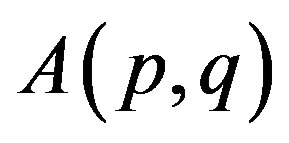 .
.
NOTES
*Corresponding author.

