Advances in Linear Algebra & Matrix Theory
Vol.06 No.04(2016), Article ID:72281,15 pages
10.4236/alamt.2016.64010
On Characterization of Poised Nodes for a Space of Bivariate Functions
Hayk Avdalyan, Hakop Hakopian
Department of Informatics and Applied Mathematics, Yerevan State University, Yerevan, Armenia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 6, 2016; Accepted: November 25, 2016; Published: November 28, 2016
ABSTRACT
There are several examples of spaces of univariate functions for which we have a characterization of all sets of knots which are poised for the interpolation problem. For the standard spaces of univariate polynomials, or spline functions the mentioned results are well-known. In contrast with this, there are no such results in the bivariate case. As an exception, one may consider only the Pascal classic theorem, in the interpolation theory interpretation. In this paper, we consider a space of bivariate piecewise linear functions, for which we can readily find out whether the given node set is poised or not. The main tool we use for this purpose is the reduction by a basic subproblem, introduced in this paper.
Keywords:
Bivariate Interpolation Problem, Poisedness, Fundamental Function, Bivariate Piecewise Linear Function, Reductions by Basic Subproblems

1. Introduction
Consider the interpolation problem with a finite dimensional space of univariate func- tions S and a set of knots 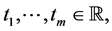 that is for a given data
that is for a given data 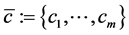 find a function
find a function 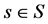 satisfying the conditions
satisfying the conditions
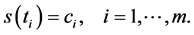 (1)
(1)
We say that the set of knots is poised for S if for any data 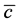 there is a unique function
there is a unique function 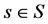 satisfying the conditions (1). A necessary condition of the poisedness is
satisfying the conditions (1). A necessary condition of the poisedness is
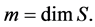
There are several cases of spaces S of univariate functions for which we have a characterization of all poised sets.
Suppose that 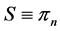 is the space of polynomials of degree at most n. We have that
is the space of polynomials of degree at most n. We have that 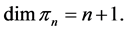 Then, according to the Lagrange theorem, all sets of knots
Then, according to the Lagrange theorem, all sets of knots 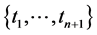 are poised.
are poised.
Now suppose that 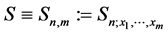 is the space of spline functions of order n and
is the space of spline functions of order n and 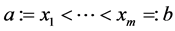 are the knots of the space (see, e.g., [1] ). Here
are the knots of the space (see, e.g., [1] ). Here 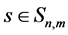 means that s is piecewise polynomial function of degree at most
means that s is piecewise polynomial function of degree at most 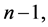 s vanishes outside of the segment
s vanishes outside of the segment 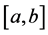 and s belongs to the differentiability class
and s belongs to the differentiability class 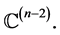 We have that
We have that 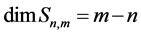 and the set of interpolation knots
and the set of interpolation knots 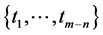 is poised if and only if the following conditions are satisfied:
is poised if and only if the following conditions are satisfied:
![]()
This result is due to Schoenberg and Whitney [2] [3] . In the univariate case there are also several characterization results concerning the trigonometric interpolation.
In contrast with this there are no such results in the bivariate case. As an exception one may consider only the Pascal classic theorem, in the interpolation theory inter- pretation (see, e.g., [4] ). To present it let ![]() be the space of bivariate polynomials of total degree at most 2. We have that
be the space of bivariate polynomials of total degree at most 2. We have that ![]() Let also
Let also ![]() be the space of bivariate linear functions,
be the space of bivariate linear functions, ![]() Then consider any set of 6 nodes
Then consider any set of 6 nodes ![]() in the plane. Construct 3 new nodes as follows:
in the plane. Construct 3 new nodes as follows:
![]()
where ![]() is the line passing through the nodes
is the line passing through the nodes ![]() and
and ![]() Then according to the Pascal theorem the 6 nodes
Then according to the Pascal theorem the 6 nodes ![]() are lying in a conic if and only if the 3 nodes
are lying in a conic if and only if the 3 nodes ![]() are collinear. To arrange the case connected with the parallel pairs of lines one may replace the plane with the projective one. The interpolation version of this result is:
are collinear. To arrange the case connected with the parallel pairs of lines one may replace the plane with the projective one. The interpolation version of this result is:
Theorem 1.1 (Pascal) Any 6 nodes ![]() in the plane are poised for
in the plane are poised for ![]() if and only if the set of respective 3 nodes
if and only if the set of respective 3 nodes ![]() is poised for
is poised for ![]()
Note that the latter poisedness condition with ![]() merely means that
merely means that ![]() are not collinear.
are not collinear.
Next we are going to introduce the space of bivariate functions we will consider in this paper. For this we need some preliminaries.
Let us define a strip of triangles. Fix a sequence of points in the plane
![]()
for the vertices of triangles. Then consider the n triangles
![]() (2)
(2)
Note that by a triangle we mean the closed set bounded by the sides of the triangle. The sequence of the triangles
![]()
makes a triangulation of the following strip (see Figure 1)
![]()
Sometimes it is convenient to call itself ![]() a strip, too.
a strip, too.
Here we require that the intersection of any neighboring triangles ![]() and
and
![]() is the common side
is the common side ![]() any pair of triangles
any pair of triangles ![]() and
and
![]() have a single common point which is the vertex
have a single common point which is the vertex ![]() and all the other pairs of the triangles are disjoint.
and all the other pairs of the triangles are disjoint.
It is easily seen that the sides ![]() together with the sides
together with the sides ![]() and
and ![]() form the boundary of the strip
form the boundary of the strip ![]() (see Figure 1). We call these sides boundary sides. The remaining sides of the triangles are called interior sides of the strip. Let us call also the sides
(see Figure 1). We call these sides boundary sides. The remaining sides of the triangles are called interior sides of the strip. Let us call also the sides ![]() and
and ![]() the left and right (boundary) sides of the strip
the left and right (boundary) sides of the strip ![]() respectively, and denote
respectively, and denote
![]()
For a triangle ![]() given in (2) we call the sides
given in (2) we call the sides ![]() and
and ![]() the left and right sides of it, respectively.
the left and right sides of it, respectively.
Denote by ![]() the linear space of continuous piecewise linear functions on
the linear space of continuous piecewise linear functions on ![]() More precisely,
More precisely, ![]() means that
means that
i) ![]()
ii) ![]()
Here ![]() means the restriction of s on D.
means the restriction of s on D.
Definition 1.2 A set of nodes ![]() is called poised for the space
is called poised for the space ![]() if for any data
if for any data ![]() the interpolation problem
the interpolation problem
![]() (3)
(3)
has exactly one solution ![]()
Let us denote the interpolation problem (3) by ![]()
The aim of this paper is the characterization of all poised sets for the space ![]() The following is a necessary condition of the poisedness:
The following is a necessary condition of the poisedness:
![]() (4)
(4)
To prove this consider the fundamental functions of the interpolation
![]() defined by the interpolation conditions
defined by the interpolation conditions
![]()
where ![]() is the symbol of Kronecker.
is the symbol of Kronecker.
Obviously the fundamental functions are linearly independent and for the solution of the interpolation problem (3) we have the following formula of Lagrange:
![]()
Thus, the fundamental functions form a basis for ![]() and we get (4).
and we get (4).
Now, let us show that the set of vertices ![]() is a poised set for
is a poised set for ![]() Indeed, having the values of a linear function at the vertices of a triangle
Indeed, having the values of a linear function at the vertices of a triangle ![]() we recover it in a unique way on the triangle. On the other hand it is easily seen that the recovered piecewise linear function is continuous on
we recover it in a unique way on the triangle. On the other hand it is easily seen that the recovered piecewise linear function is continuous on ![]() Thus, the dimension of
Thus, the dimension of ![]() equals to the number of the vertices in the strip
equals to the number of the vertices in the strip ![]()
![]() (5)
(5)
In view of (4) we obtain that any poised set ![]() for the space
for the space ![]() consists of
consists of ![]() nodes:
nodes:
![]() (6)
(6)
Let us call interpolation problem ![]() satisfying this condition exact. In the cases
satisfying this condition exact. In the cases ![]() and
and ![]() we call the problem
we call the problem ![]() underdetermined and over- determined, respectively.
underdetermined and over- determined, respectively.
Denote by
![]()
the fundamental polynomials with respect to the poised set![]() . They form a basis for the space
. They form a basis for the space ![]() Thus we have the following representation for any piecewise linear function
Thus we have the following representation for any piecewise linear function ![]()
![]()
In view of this representation the interpolation problem (3) reduces to m linear equations with ![]() unknowns, which are the values a piecewise linear function at the vertices
unknowns, which are the values a piecewise linear function at the vertices![]() . Hence an exact interpolation problem
. Hence an exact interpolation problem ![]() is poised if and only if the following Vandermonde determinant does not vanish:
is poised if and only if the following Vandermonde determinant does not vanish:
![]() (7)
(7)
where
![]()
Thus our main problem can be formulated in terms of Vandermonde determinant in the following way:
Characterize all exact sets ![]() for which the Vandermonde determinant does not vanish, i.e., (7) holds.
for which the Vandermonde determinant does not vanish, i.e., (7) holds.
The following two propositions are basic Linear Algebra facts.
Proposition 1.3 Given an exact problem ![]() Then each of the following con- ditions is equivalent to the poisedness of
Then each of the following con- ditions is equivalent to the poisedness of![]() :
:
i) All fundamental functions ![]() exist.
exist.
ii) ![]()
Proposition 1.4 Given a problem ![]() Then the following hold:
Then the following hold:
i) If the problem is underdetermined then there is a function ![]() such that
such that
![]()
ii) If the problem is overderdetermined then there is a node in ![]() for which no fundamental function exists.
for which no fundamental function exists.
2. Subproblems
For a given strip ![]() denote by
denote by ![]() the following part of it
the following part of it
![]()
For a problem ![]() denote by
denote by ![]() the subproblem with the function space
the subproblem with the function space ![]() and the set of nodes
and the set of nodes ![]() i.e.,
i.e.,
![]()
Problems with Boundary Conditions
Denote by ![]() the linear space of continuous piecewise linear functions on
the linear space of continuous piecewise linear functions on ![]() vanishing at the left (boundary) side of the strip
vanishing at the left (boundary) side of the strip![]() , i.e.,
, i.e.,
![]()
In the similar way one can define the space of functions vanishing at the right side of the strip ![]() i.e.,
i.e.,
![]()
One may define also the space of functions vanishing at the both left and right sides of the strip ![]() i.e.,
i.e.,
![]()
By counting the number of vertices of the strip where a function from the space may differ from ![]() we get, in the same way as in the proof of (5), that
we get, in the same way as in the proof of (5), that
![]()
Denote the interpolation problems with the spaces ![]()
![]() and a node set
and a node set ![]() by
by ![]()
![]()
![]() respectively.
respectively.
As we will see below the poisedness of interpolation problems with boundary con- ditions readily can be reduced to the previous general interpolation problems by just adding two nodes in the left or/and right sides of the strip.
For this purpose it is convenient to use the following notation for the strip ![]()
![]()
where ![]() and
and ![]() are the two vertices of
are the two vertices of ![]()
![]()
where ![]() and
and ![]() are the two vertices of
are the two vertices of ![]() Denote also
Denote also
![]()
Let us call two interpolation problems equivalent if both they are poised or both they are not poised. By using Proposition 1.3, ii), we readily get
Proposition 2.1 The folllwing pairs of interpolation problems are equivalent:
![]() and
and ![]()
![]() and
and ![]()
![]() and
and ![]()
Note that in the subproblem ![]() we have that
we have that
![]()
where ![]() and
and ![]() are the two vertices of
are the two vertices of ![]() The situation is similar with the sets
The situation is similar with the sets ![]() and
and ![]()
3. Reductions of Interpolation Problems
Below we bring a main theorem regarding the reduction of an interpolation problem having an exact or overdetermined subproblem.
Theorem 3.1 Suppose that ![]() is an exact problem where the strip
is an exact problem where the strip ![]() consists of n triangles and
consists of n triangles and ![]() is a subproblem, where
is a subproblem, where![]() .
.
Then the following hold.
i) If the subproblem ![]() is exact and not poised, or overdetermined, then the problem
is exact and not poised, or overdetermined, then the problem ![]() is not poised.
is not poised.
ii) If the subproblem ![]() is poised then the problem
is poised then the problem ![]() is poised if and only if the both following two reduced problems
is poised if and only if the both following two reduced problems
![]() (8)
(8)
are exact and poised.
Note that in the cases ![]() and
and ![]() we have just one reduced problem instead of two.
we have just one reduced problem instead of two.
Proof. Suppose first that the subproblem ![]() is exact and not poised, or overdetermined. Then, in view of Propositions 1.3, i), and 1.4, ii), there is a node
is exact and not poised, or overdetermined. Then, in view of Propositions 1.3, i), and 1.4, ii), there is a node ![]() which does not have a fundamental function. Then, evidently the same node A does not have a fundamental function for the whole node set
which does not have a fundamental function. Then, evidently the same node A does not have a fundamental function for the whole node set ![]() too. Hence, in view of Proposition 1.3, i), we get that the problem
too. Hence, in view of Proposition 1.3, i), we get that the problem ![]() is not poised.
is not poised.
Now consider the case when the subproblem ![]() is poised.
is poised.
Let us assume that the both reduced problems in (8) are poised. Then let us prove that the problem ![]() is poised, too. Notice first that the problem
is poised, too. Notice first that the problem ![]() is exact. Thus, by following Proposition 1.3, ii), assume that
is exact. Thus, by following Proposition 1.3, ii), assume that ![]() Now, since the subproblem
Now, since the subproblem ![]() is poised, we conclude that s vanishes on the triangles
is poised, we conclude that s vanishes on the triangles ![]() Therefore s vanishes at the right side of the triangle
Therefore s vanishes at the right side of the triangle ![]() and at the left side of the triangle
and at the left side of the triangle ![]() Thus we have that
Thus we have that ![]() and
and ![]() Finally, since the problems in (8) are poised, we obtain that s vanishes on the triangles
Finally, since the problems in (8) are poised, we obtain that s vanishes on the triangles ![]() and
and ![]() Hence s vanishes on all triangles of
Hence s vanishes on all triangles of ![]()
Next let us assume that the problem ![]() is poised and prove that the both reduced problems in (8) are poised, too. Let us show first that these reduced problems are exact. There are
is poised and prove that the both reduced problems in (8) are poised, too. Let us show first that these reduced problems are exact. There are ![]() and
and ![]() triangles in the reduced problems (8), respectively. Thus for exactness we need
triangles in the reduced problems (8), respectively. Thus for exactness we need ![]() and
and ![]() nodes, respectively, altogether
nodes, respectively, altogether
![]() nodes. It is easily seen that indeed, in two mentioned problems together we have that many nodes. Indeed, this is the number of the nodes in
nodes. It is easily seen that indeed, in two mentioned problems together we have that many nodes. Indeed, this is the number of the nodes in ![]() minus the number of the nodes in
minus the number of the nodes in ![]() and plus 4, i.e.,
and plus 4, i.e., ![]()
Latter ![]() nodes come from the added nodes in the boundary in the node sets
nodes come from the added nodes in the boundary in the node sets ![]() and
and![]() .
.
Now, assume by way of contradiction that a subproblem in (8) is not exact. Therefore one of the subproblems, say the first problem in (8), is underdetermined, and another is overdetermined. Then, in view of Proposition 1.4, i), there is a function ![]() such that
such that
![]() (9)
(9)
Thus s here vanishes on ![]() and, since of “+2”, also on the right side of the triangle
and, since of “+2”, also on the right side of the triangle ![]() Now let us extend this function s from
Now let us extend this function s from ![]() till the whole strip
till the whole strip ![]() by defining it to be 0 on the triangles
by defining it to be 0 on the triangles ![]() Denote by
Denote by ![]() the extended function. Then it is easily seen that
the extended function. Then it is easily seen that ![]() and
and ![]() This, in view of Proposition 1.3, ii), means that the problem
This, in view of Proposition 1.3, ii), means that the problem ![]() is not poised, which contradicts our assumption.
is not poised, which contradicts our assumption.
Finally, let us show that the both reduced problems in (8) are poised. Assume by way of contradiction that one of them, say the first, is not poised. Since it is exact, we can use Proposition 1.3, ii), to get that there is a function ![]() such that the relation (9) is satisfied. From here we continue in the same way as in the above step, after the relation (9).
such that the relation (9) is satisfied. From here we continue in the same way as in the above step, after the relation (9).
4. The Basic Interpolation Problems
Let us denote by “3” the problem with a strip consisting of a triangle and at least three nodes inside. The respective basic problem, denoted briefly by “![]() ”, is a “3” problem with exactly three nodes, which are non-collinear.
”, is a “3” problem with exactly three nodes, which are non-collinear.
Then, let us denote by “![]() ” the problem with a strip consisting of two triangles and exactly two nodes in each of them. Note that in this case no node can lie in the interior side of the strip. We call a problem “
” the problem with a strip consisting of two triangles and exactly two nodes in each of them. Note that in this case no node can lie in the interior side of the strip. We call a problem “![]() ” basic and denote it by “
” basic and denote it by “![]() ” if in each triangle the line passing through the two nodes there does not intersect the other triangle. Note that in the case of “
” if in each triangle the line passing through the two nodes there does not intersect the other triangle. Note that in the case of “![]() ” problem no node can coincide with a vertex of the strip.
” problem no node can coincide with a vertex of the strip.
Next consider an interpolation problem denoted by “![]() ” where m is the number of 1’s. This is the interpolation problem with a strip consisting of
” where m is the number of 1’s. This is the interpolation problem with a strip consisting of ![]() triangles such that each of the first and the last triangles contains exactly two nodes and each of the other m triangles contains exactly a node. Note that in this case no node can be located in an interior side of the strip. We call a problem “
triangles such that each of the first and the last triangles contains exactly two nodes and each of the other m triangles contains exactly a node. Note that in this case no node can be located in an interior side of the strip. We call a problem “![]() ” basic and denote it by “
” basic and denote it by “![]() ” if the line passing through the two nodes in each of the first and the last triangles does not intersect the neighboring triangle.
” if the line passing through the two nodes in each of the first and the last triangles does not intersect the neighboring triangle.
Note that the “![]() ” problem can be considered as a special case of the
” problem can be considered as a special case of the
“![]() ” problem, where
” problem, where ![]()
The Poisedness of the Basic Problems
Let us start this section with a simple lemma. Suppose that two nodes ![]() of a node set
of a node set ![]() belong to a triangle of
belong to a triangle of ![]() Denote by
Denote by ![]() the points of intersection of the line passing through
the points of intersection of the line passing through ![]() and
and ![]() with the sides of the triangle. Let us call
with the sides of the triangle. Let us call ![]() the intersection pair of
the intersection pair of ![]() Denote by
Denote by ![]() the set of the nodes received from
the set of the nodes received from ![]() by replacing the pair
by replacing the pair ![]() with
with ![]() there. We call the set
there. We call the set ![]() the line trans- formation of the set
the line trans- formation of the set ![]() with respect to the pair
with respect to the pair ![]()
Two node sets ![]() and
and ![]() are called line-equivalent if one of them can be obtained from the other by means of several line transformations.
are called line-equivalent if one of them can be obtained from the other by means of several line transformations.
Lemma 4.1 The exact interpolation problems ![]() and
and ![]() are equivalent, if the node sets
are equivalent, if the node sets ![]() and
and ![]() are line-equivalent.
are line-equivalent.
Proof. In view of Proposition 1.3, ii), it suffices to verify that
![]() (10)
(10)
where the node set ![]() is the line transformation of the set
is the line transformation of the set ![]() with respect to an appropriate pair of nodes
with respect to an appropriate pair of nodes ![]() Now notice that (10) readily follows from the evident fact that
Now notice that (10) readily follows from the evident fact that
![]()
where ![]() is the intersection pair of
is the intersection pair of ![]() Indeed, each side of this equiva- lence means merely that
Indeed, each side of this equiva- lence means merely that ![]() vanishes on the line passing through
vanishes on the line passing through ![]() and
and ![]()
The proof of the following proposition contains an easy algorithm for verifying the poisedness of basic problems.
Proposition 4.2 The problems “![]() ” and “
” and “![]() ” are always poised.
” are always poised.
The problem “![]() ” where
” where ![]() may be poised or not, depen- ding on the configuration of nodes. Moreover, if the problem is not poised then it becomes poised after changing the location of one of the two nodes in the first or the last triangle, such that the slope of the line passing through the two nodes is changed.
may be poised or not, depen- ding on the configuration of nodes. Moreover, if the problem is not poised then it becomes poised after changing the location of one of the two nodes in the first or the last triangle, such that the slope of the line passing through the two nodes is changed.
Note that the case ![]() here concerns the problem “
here concerns the problem “![]() ”
”
Proof. The case of “![]() ” is obvious.
” is obvious.
Consider the problem “![]() ” (see Figure 2). Suppose that
” (see Figure 2). Suppose that ![]()
and![]() , where
, where ![]()
![]() In view of Lem- ma 4.1 we may replace the node set
In view of Lem- ma 4.1 we may replace the node set ![]() with the set
with the set ![]() where
where ![]() and
and ![]() are the intersection pairs of the respective pairs from
are the intersection pairs of the respective pairs from ![]() Since the problem
Since the problem ![]() is basic we have that the nodes
is basic we have that the nodes ![]() belong to the four sides of the triangles
belong to the four sides of the triangles ![]() and
and ![]() which are boundary sides of the strip
which are boundary sides of the strip ![]() one node in each side (see Figure 2). Now suppose by way of contradiction that the problem
one node in each side (see Figure 2). Now suppose by way of contradiction that the problem ![]() is not poised. This in view of Proposition 1.3, ii), means that there is a function
is not poised. This in view of Proposition 1.3, ii), means that there is a function ![]() such that
such that ![]() while
while ![]() Then it is easily seen that
Then it is easily seen that ![]() and therefore
and therefore ![]() Assume without loss of generality that
Assume without loss of generality that ![]() Then, since s is linear and
Then, since s is linear and ![]() we get readily that
we get readily that ![]() and
and ![]() Now, in view of the latter condition and
Now, in view of the latter condition and ![]() we get readily that
we get readily that ![]() and
and ![]() Thus s assumes negative values at all the vertices of the triangle
Thus s assumes negative values at all the vertices of the triangle ![]() and it vanishes at
and it vanishes at ![]() which is a contradiction.
which is a contradiction.
Finally, consider the problem “![]() ” where
” where ![]() Suppose that
Suppose that ![]() and
and![]() , where
, where ![]()
Assume that the problem ![]() is not poised. This in view of Proposition 1.3, ii), means that there is a function s such that
is not poised. This in view of Proposition 1.3, ii), means that there is a function s such that
![]() (11)
(11)
It is easily seen that ![]() Indeed,
Indeed, ![]() implies that s vanishes at the left side of
implies that s vanishes at the left side of ![]() Then, in view of the condition
Then, in view of the condition ![]() where
where ![]() we conclude that
we conclude that ![]() Notice that
Notice that ![]() does not belong to the left (or right) side of the triangle, since the problem is basic. Continuing this way we obtain
does not belong to the left (or right) side of the triangle, since the problem is basic. Continuing this way we obtain ![]() and thus
and thus ![]() contradicting our assumption. In the same way we get that
contradicting our assumption. In the same way we get that
![]() (12)
(12)
By replacing s, if necessary, with a nonzero constant multiple of it, assume that ![]() Now, in view of the condition
Now, in view of the condition ![]() where
where ![]() the func- tion
the func- tion ![]() is determined on
is determined on ![]() Indeed, the nodes
Indeed, the nodes ![]() are not collinear since the problem is basic. Hence s is determined at the left side of the second triangle
are not collinear since the problem is basic. Hence s is determined at the left side of the second triangle ![]() Next, we have that
Next, we have that ![]() where
where ![]() does not belong to the left (or right) side of the triangle. Thus we get that s is determined on
does not belong to the left (or right) side of the triangle. Thus we get that s is determined on ![]() Continuing this way we get that s is determined on
Continuing this way we get that s is determined on ![]() Now s is determined at the left side of the last triangle
Now s is determined at the left side of the last triangle ![]() By using the condition
By using the condition ![]() where
where ![]() we con- clude, in view of (12), that the zero set of s in
we con- clude, in view of (12), that the zero set of s in ![]() is a line
is a line ![]() passing through
passing through ![]() Thus if the last node
Thus if the last node ![]() lies in this line then we have that s vanishes at
lies in this line then we have that s vanishes at ![]() too. Hence the condition (11) holds, which, in view of Proposition 1.3, ii), means that the problem is not poised. While the condition
too. Hence the condition (11) holds, which, in view of Proposition 1.3, ii), means that the problem is not poised. While the condition ![]() implies that s vanishes on
implies that s vanishes on ![]() which contradicts (12) and whence (11). Thus the problem is poised in this case. This consideration makes clear also the “moreover” part of Proposition.
which contradicts (12) and whence (11). Thus the problem is poised in this case. This consideration makes clear also the “moreover” part of Proposition.
It is worth mentioning that if the restriction of s on the left side of triangle ![]() has a zero (as it will happen in the case of “
has a zero (as it will happen in the case of “![]() ”) denoted by C then the basic problem is poised, wherever the two last nodes
”) denoted by C then the basic problem is poised, wherever the two last nodes ![]() and
and ![]() are situated. Indeed, otherwise we would have that the zero-line
are situated. Indeed, otherwise we would have that the zero-line ![]() of s in the last triangle passes through
of s in the last triangle passes through ![]() and C, which contradicts the fact that the problem is basic.
and C, which contradicts the fact that the problem is basic.
5. Reductions by Basic Subproblems
5.1. Reduction by “3/B”
In the case of basic subproblem “![]() ” we have a poised subproblem with one triangle. Thus we get from Theorem 3.1, ii), the following
” we have a poised subproblem with one triangle. Thus we get from Theorem 3.1, ii), the following
Corollary 5.1 Assume that ![]() is an exact problem, where the strip consists of n triangles. Assume also that a triangle
is an exact problem, where the strip consists of n triangles. Assume also that a triangle ![]() contains exactly 3 non-collinear nodes. Then the interpolation problem
contains exactly 3 non-collinear nodes. Then the interpolation problem ![]() is poised if and only if the both following two reduced problems
is poised if and only if the both following two reduced problems
![]() (13)
(13)
are exact and poised.
Note that in the cases ![]() and
and ![]() we have just one reduced problem instead of two.
we have just one reduced problem instead of two.
5.2. Reduction by “2 + 1 + ・・・ + 1 + 2/B”
For this case we get from Theorem 3.1 the following
Corollary 5.2 Assume that ![]() is an exact problem, where the strip consists of n triangles. Assume also that the subproblem
is an exact problem, where the strip consists of n triangles. Assume also that the subproblem ![]() is basic of type “
is basic of type “![]() ,” where
,” where ![]() Then the problem is not poised if the subproblem is not poised. In the case when the subproblem is poised the problem
Then the problem is not poised if the subproblem is not poised. In the case when the subproblem is poised the problem ![]() is poised if and only if the both following two reduced problems
is poised if and only if the both following two reduced problems
![]() (14)
(14)
are exact and poised.
Note that in the cases ![]() and
and ![]() we have just one reduced problem instead of two.
we have just one reduced problem instead of two.
Since, by Proposition 4.2, the basic problems of type “![]() ” are always poised we get from Theorem 3.1, ii), the following
” are always poised we get from Theorem 3.1, ii), the following
Corollary 5.3 Assume that ![]() is an exact problem, where the strip consists of n triangles. Assume also that the subproblem
is an exact problem, where the strip consists of n triangles. Assume also that the subproblem ![]() is basic of type “
is basic of type “![]() ”. Then the problem
”. Then the problem ![]() is poised if and only if the both following two reduced problems
is poised if and only if the both following two reduced problems
![]()
are exact and poised.
Note that in the cases ![]() and
and ![]() we have just one reduced problem instead of two.
we have just one reduced problem instead of two.
6. Existence of a Reduction
In this section we prove that every exact problem has a subproblem of type “3”, “![]() ”, or “
”, or “![]() ”. Next, we show that by applying line-transformations to this subproblem, we can reduce it to a basic subproblem or determine that the given exact problem is not poised. After this, by following the algorithm pointed out in the proof of Proposition 4.2, we may verify whether the basic subproblem is poised or not. If not then, in view of Theorem 3.1, i), we conclude that the given exact problem is not poised either. If the basic subproblem is poised then we may apply the respective reduction, given by Corollaries 5.1, 5.2, or 5.3. Thus we have a complete solution of the poisedness problem.
”. Next, we show that by applying line-transformations to this subproblem, we can reduce it to a basic subproblem or determine that the given exact problem is not poised. After this, by following the algorithm pointed out in the proof of Proposition 4.2, we may verify whether the basic subproblem is poised or not. If not then, in view of Theorem 3.1, i), we conclude that the given exact problem is not poised either. If the basic subproblem is poised then we may apply the respective reduction, given by Corollaries 5.1, 5.2, or 5.3. Thus we have a complete solution of the poisedness problem.
Theorem 6.1 Assume that ![]() is an exact problem. Then it has a subproblem of type “3”, “
is an exact problem. Then it has a subproblem of type “3”, “![]() ”, or “
”, or “![]() ”. Moreover, by using line-transformations, we either determine that the problem is not poised, or we reduce the node set
”. Moreover, by using line-transformations, we either determine that the problem is not poised, or we reduce the node set ![]() to
to ![]() such that the line-equivalent problem
such that the line-equivalent problem ![]() has a basic subproblem of type “
has a basic subproblem of type “![]() ”, “
”, “![]() ”, or “
”, or “![]() ”.
”.
Proof. Suppose that a triangle contains more than 3 nodes, or exactly 3 collinear nodes. Then the problem obviously is not poised and also we have a type “3” sub- problem. If a triangle contains exactly 3 non-collinear nodes then we have a type “![]() ” basic subproblem.
” basic subproblem.
Now, let us assume that no triangle of ![]() contains more than 2 nodes.
contains more than 2 nodes.
Step 1. Let us verify that the problem ![]() contains a subproblem of type “
contains a subproblem of type “![]() ”, or “
”, or “![]() ”.
”.
Let us throw away those triangles of ![]() which do not contain nodes from
which do not contain nodes from ![]() Let us throw away also those triangles of
Let us throw away also those triangles of ![]() which contain just one node from
which contain just one node from ![]() located in an interior side of
located in an interior side of ![]() By saying a node is thrown we mean that it does not belong to the remained triangles.
By saying a node is thrown we mean that it does not belong to the remained triangles.
Notice that only a node located in an interior side of the strip can be thrown. Moreover, this can happen only if the both neighboring triangles were thrown, i.e., if it is the only node in the interior side and also the only node in the both neighboring triangles.
Assume that after this operation the connected blocks of remained triangles in ![]() are
are
![]() (15)
(15)
where ![]()
Now, let us verify that for a block here the number of nodes (from![]() ) is greater or equal to the number of triangles plus two.
) is greater or equal to the number of triangles plus two.
Assume by way of contradiction that for all blocks in (15) the number of nodes does not exceed the number of triangles plus one. Then we get that the number of nodes in all above connected blocks is less than or equal to the number of triangles in all connected pieces plus![]() , where
, where ![]() is the number of blocks in (15).
is the number of blocks in (15).
Next, consider the breaks, i.e., the dropped blocks. For each break we have that the number of nodes, i.e., number of the thrown nodes in the above mentioned operation, is less than or equal to the number of triangles there minus 1. Indeed, a such node (in an interior side of![]() ) is thrown if both triangles containing it where thrown. Thus we can assign two thrown triangles to each thrown node. Also note that all the triangles assigned are different. Hence the number of nodes in all above mentioned breaks is less than or equal to the number of the triangles there minus
) is thrown if both triangles containing it where thrown. Thus we can assign two thrown triangles to each thrown node. Also note that all the triangles assigned are different. Hence the number of nodes in all above mentioned breaks is less than or equal to the number of the triangles there minus![]() , since there are at least
, since there are at least ![]() breaks.
breaks.
Thus we may conclude that the number of nodes in ![]() does not exceed the number of triangles there plus
does not exceed the number of triangles there plus ![]() This contradicts the assumption that the pro- blem
This contradicts the assumption that the pro- blem ![]() is exact.
is exact.
Now assume, without loss of generality, that in the first block ![]() the number of nodes from
the number of nodes from ![]() is greater or equal to the number of triangles there plus two. Note that if a triangle in this block contains only one node then it is not located in its left or right side, otherwise the triangle would be thrown away before.
is greater or equal to the number of triangles there plus two. Note that if a triangle in this block contains only one node then it is not located in its left or right side, otherwise the triangle would be thrown away before.
Since no triangle contains three nodes, we get that there is a triangle in this block containing two nodes. Consider the first such triangle ![]() i.e., a such triangle with the minimal subscript
i.e., a such triangle with the minimal subscript ![]() If both the two nodes here are lying in the right side of the triangle then the next triangle
If both the two nodes here are lying in the right side of the triangle then the next triangle ![]() contains only these two nodes. Now notice that in the triangles from
contains only these two nodes. Now notice that in the triangles from ![]() till
till ![]() the number of nodes equals to
the number of nodes equals to ![]() i.e., the number of triangles here. This means that there is another triangle in the first block, following
i.e., the number of triangles here. This means that there is another triangle in the first block, following ![]() containing two nodes, such that at least one node is not lying in the right side of the triangle.
containing two nodes, such that at least one node is not lying in the right side of the triangle.
Then consider the first such triangle ![]() If one of the two nodes here is in the right side of the triangle then the next triangle
If one of the two nodes here is in the right side of the triangle then the next triangle ![]() also contains two nodes, because otherwise it would be thrown away before. Now notice that in the triangles from
also contains two nodes, because otherwise it would be thrown away before. Now notice that in the triangles from ![]() till
till ![]() the number of nodes does not exceeds
the number of nodes does not exceeds ![]() i.e., the number of triangles here plus 1. This means that there is another triangle in this series, denoted by
i.e., the number of triangles here plus 1. This means that there is another triangle in this series, denoted by ![]() following
following ![]() containing two nodes, which do not lie in its right side. This will be the first triangle of the desired subproblem.
containing two nodes, which do not lie in its right side. This will be the first triangle of the desired subproblem.
Now notice that in the triangles from ![]() till
till ![]() the number of nodes equals to
the number of nodes equals to ![]() i.e., the number of triangles here plus 1. This means that there is another triangle in the first block, following
i.e., the number of triangles here plus 1. This means that there is another triangle in the first block, following ![]() containing two nodes. Denote by
containing two nodes. Denote by ![]() the first such triangle. This will be the last triangle of the desired subproblem. First notice that each triangle between
the first such triangle. This will be the last triangle of the desired subproblem. First notice that each triangle between ![]() and
and ![]() if there is a such, contains just one node, which, as was mentioned earlier, cannot be located in its left or right side. Therefore no node in
if there is a such, contains just one node, which, as was mentioned earlier, cannot be located in its left or right side. Therefore no node in ![]() belongs to the left side of the triangle, since otherwise
belongs to the left side of the triangle, since otherwise ![]() would con- tain a node in its right side. Note also that in this case
would con- tain a node in its right side. Note also that in this case ![]() does not coincide with
does not coincide with ![]() since the latter has no node in its right side.
since the latter has no node in its right side.
Thus the subproblem ![]() is of type “
is of type “![]() ”, or “
”, or “![]() ” with
” with ![]()
Step 2. Next, by using line-transformations, we either reduce this subproblem to a basic subproblem or determine that the problem ![]() is not poised.
is not poised.
First suppose that the subproblem ![]() is of type “
is of type “![]() ”. If it is not basic then the line through the two nodes in a triangle intersects its interior side. Then by replacing these two nodes with their intersection pair we will have in the other triangle one more node, i.e., three nodes. This case was considered in the beginning of the proof.
”. If it is not basic then the line through the two nodes in a triangle intersects its interior side. Then by replacing these two nodes with their intersection pair we will have in the other triangle one more node, i.e., three nodes. This case was considered in the beginning of the proof.
Finally, suppose that the subproblem ![]() is of type “
is of type “![]() ”, with
”, with ![]() Now, if this subproblem is not basic then in the same way as in the previous case we may reduce it by line transformation to a problem of the same type, where the number of 1’s equals to
Now, if this subproblem is not basic then in the same way as in the previous case we may reduce it by line transformation to a problem of the same type, where the number of 1’s equals to ![]() Thus we may complete readily the proof by using in- duction on m, where the first step of induction corresponds to the case
Thus we may complete readily the proof by using in- duction on m, where the first step of induction corresponds to the case ![]() considered already.
considered already.
7. Final Remarks
7.1. Some Necessary Conditions of Poisedness
Consider a problem ![]() where the strip consists of n triangles. Denote the number of nodes from
where the strip consists of n triangles. Denote the number of nodes from ![]() in the triangles
in the triangles ![]() by
by ![]()
![]()
The following proposition gives some necessary conditions of poisedness.
Proposition 7.1 Given a poised problem ![]() where the strip consists of n triangles. Then for each k and
where the strip consists of n triangles. Then for each k and ![]() we have that
we have that
![]() (16)
(16)
Moreover, in the cases ![]() and
and ![]() we have stricter inequalities:
we have stricter inequalities:
![]() (17)
(17)
Proof. Let us prove first the right inequality in (16):
![]() (18)
(18)
Indeed, suppose conversely that ![]() Then the subproblem
Then the subproblem ![]() is overdetermined. Therefore the problem
is overdetermined. Therefore the problem ![]() in view of Theorem 3.1, is not poised, which is a contradiction.
in view of Theorem 3.1, is not poised, which is a contradiction.
In particular, we get from (18) that
![]() (19)
(19)
Now, in view of the relations ![]() and
and ![]() we get the inequalities in the left sides in (17).
we get the inequalities in the left sides in (17).
Finally, let us verify the left inequality in (16). In view of (19) we have
![]()
From the particular case ![]() of (16) we have that
of (16) we have that
![]()
Therefore, if in an exact problem ![]() some three successive triangles do not contain nodes then the problem is not poised.
some three successive triangles do not contain nodes then the problem is not poised.
Also, in view of (17), we have that an exact problem is not poised if there are no nodes in the first or the last triangles of the strip.
In the last subsection we consider the case when there are no nodes in two successive triangles which do not include the first or the last triangles of the strip.
7.2. Reduction “0 + 0”
Theorem 7.2 Given an exact problem ![]() where the strip consists of n triangles. Suppose that some two successive triangles
where the strip consists of n triangles. Suppose that some two successive triangles ![]() and
and ![]() where
where ![]() do not contain nodes. Then the problem
do not contain nodes. Then the problem ![]() is poised if and only if the both fol- lowing two reduced problems
is poised if and only if the both fol- lowing two reduced problems
![]() (20)
(20)
are exact and poised.
Proof. Let us assume that the both reduced problems in (20) are poised. Notice that then the problem ![]() is exact. Now let us prove, by following Proposition 1.3, ii), that the problem
is exact. Now let us prove, by following Proposition 1.3, ii), that the problem ![]() is poised, too. Thus, assume that
is poised, too. Thus, assume that ![]() From here we get that
From here we get that ![]() and
and ![]() Since the two subproblems in (20) are poised, we conclude that s vanishes on the triangles
Since the two subproblems in (20) are poised, we conclude that s vanishes on the triangles ![]() and
and ![]() Therefore s vanishes also at the left side of the triangle
Therefore s vanishes also at the left side of the triangle ![]() and at the right side of the triangle
and at the right side of the triangle ![]() In particular s vanishes at all the vertices of triangles
In particular s vanishes at all the vertices of triangles ![]() and
and ![]() Thus it vanishes on these two triangles too. Hence
Thus it vanishes on these two triangles too. Hence ![]()
Next let us assume that the problem ![]() is poised and prove that the both reduced problems in (20) are poised.
is poised and prove that the both reduced problems in (20) are poised.
Let us show first that the both reduced problems in (13) are exact. There are ![]() and
and ![]() triangles in the reduced problems (20), respectively. Therefore for exact- ness we need
triangles in the reduced problems (20), respectively. Therefore for exact- ness we need ![]() and
and ![]() nodes, respectively, altogether
nodes, respectively, altogether ![]() nodes. Now, assume by way of contradiction that a subproblem in (20) is not exact. Then a sub- problem is overdetermined and the other is underdetermined. Therefore, by Theorem 3.1, i), the problem is not poised, which is a contradiction.
nodes. Now, assume by way of contradiction that a subproblem in (20) is not exact. Then a sub- problem is overdetermined and the other is underdetermined. Therefore, by Theorem 3.1, i), the problem is not poised, which is a contradiction.
Finally, let us show that both the reduced problems in (20) are poised. Assume by way of contradiction that one of them is not poised. Then again, by Theorem 3.1, i), the problem is not poised, which is a contradiction.
Cite this paper
Avdalyan, H. and Hakopian, H. (2016) On Characterization of Poised Nodes for a Space of Bivariate Functions. Advances in Linear Algebra & Matrix Theory, 6, 89-103. http://dx.doi.org/10.4236/alamt.2016.64010
References
- 1. Bojanov, B.D., Hakopian, H. and Sahakian, A. (1993) Spline Functions and Multivariate Interpolations, Mathematics and Its Applications. Vol. 248, Kluwer Acad. Publishers Group, Dordrecht.
- 2. Schoenberg, I.J. and Whitney, A. (1949) Sur la positivié des déterminants de translations des fonctions de fréquence de Pólya avec une application a une problèeme d’interpolation. C. R. Acad. Sci. Paris Ser. A, 228, 1996-1998.
- 3. Schoenberg, I.J. and Whitney, A. (1953) On Pólya Frequency Functions. III. The Positivity of Translation Determinants with an Application to the Interpolation Problem by Spline curves. Transactions of the American Mathematical Society, 74, 246-259.
- 4. Hakopian, H., Jetter, K. and Zimmermann, G. (2009) Vandermonde Matrices for Intersection Points of Curves. Jaen Journal on Approximation, 1, 67-81.





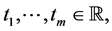 that is for a given data
that is for a given data 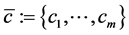 find a function
find a function 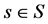 satisfying the conditions
satisfying the conditions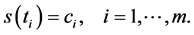 (1)
(1)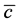 there is a unique function
there is a unique function 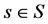 satisfying the conditions (1). A necessary condition of the poisedness is
satisfying the conditions (1). A necessary condition of the poisedness is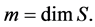
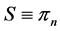 is the space of polynomials of degree at most n. We have that
is the space of polynomials of degree at most n. We have that 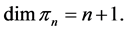 Then, according to the Lagrange theorem, all sets of knots
Then, according to the Lagrange theorem, all sets of knots 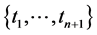 are poised.
are poised.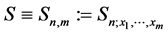 is the space of spline functions of order n and
is the space of spline functions of order n and 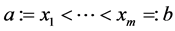 are the knots of the space (see, e.g., [1] ). Here
are the knots of the space (see, e.g., [1] ). Here 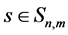 means that s is piecewise polynomial function of degree at most
means that s is piecewise polynomial function of degree at most 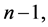 s vanishes outside of the segment
s vanishes outside of the segment 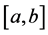 and s belongs to the differentiability class
and s belongs to the differentiability class 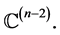 We have that
We have that 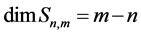 and the set of interpolation knots
and the set of interpolation knots 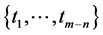 is poised if and only if the following conditions are satisfied:
is poised if and only if the following conditions are satisfied:













































































































































































































































































































































































































































































