Received 4 December 2015; accepted 4 March 2016; published 7 March 2016

ABSTRACT

Dykstra’s alternating projection algorithm was proposed to treat the problem of finding the projection of a given point onto the intersection of some closed convex sets. In this paper, we first apply Dykstra’s alternating projection algorithm to compute the optimal approximate symmetric positive semidefinite solution of the matrix equations AXB = E, CXD = F. If we choose the initial iterative matrix X₀ = 0, the least Frobenius norm symmetric positive semidefinite solution of these matrix equations is obtained. A numerical example shows that the new algorithm is feasible and effective.

Keywords:

Matrix Equation, Dykstra’s Alternating Projection Algorithm, Optimal Approximate Solution, Least Norm Solution

1. Introduction

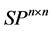Throughout this paper, we use and to stand for the set of 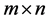real matrices and 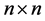symmetric positive semidefinite matrices, respectively. We denote the transpose and Moore-Penrose generalized inverse of the matrix A by 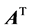and, respectively. The symbol 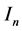stands for 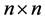identity matrix. For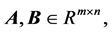 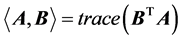denotes the inner product of the matrix A and B. The induced norm is the so-called Frobenius norm, that is, 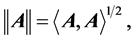then is a real Hilbert space. In order to develop this paper, we need to give the following definition.

Definition 1.1. [1] Let M be a closed convex subset in a real Hilbert space H and u be a point in H, then the point in M nearest to u is called the projection of u onto M and denoted by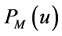, that is to say, 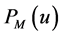is the solution of the following minimization problem

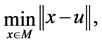(1.1)

i.e.

(1.2)

In this paper, we consider the matrix equations

(1.3)

and their matrix nearness problem.

Problem I. Given matrices and find such that

(1.4)

where

Obviously, is the symmetric positive semidefinite solution set of the matrix equations (1.3). It is easy to verify that is a closed convex set, then the solution of Problem I is unique. In this paper, the unique solution is called the optimal approximate symmetric positive semidefinite solution of Equation (1.3). In particular, if then the solution of Problem I is just the least Frobenius norm symmetric positive semidefinite solution of the matrix equations (1.3).

This kind of matrix nearness problem occurs frequently in experimental design, see for instance [2] [3] . Here may be obtained from experiments, but not satisfy Equation (1.3). The nearest matrix satisfies Equa- tion (1.3) and is nearest to the given matrix. Up to now, Equation (1.3) and their matrix nearness problem I have been extensively studied for the past 40 or more years. Navarra-Odell-Young [4] and Wang [5] gave necessary and sufficient conditions for Equation (1.3) having a solution and presented the expression for a general solution. By the projection theorem and matrix decompositions, Liao-Lei-Yuan [6] [7] gave some analytical expressions of the optimal approximate least square symmetric solution of Equation (1.3). Sheng- Chen [8] presented an efficient iterative method to compute the optimal approximate solution for the matrix equations (1.3). Ding-Liu-Ding [9] considered the unique solution of Equation (1.3) and used gradient based iterative algorithm to compute the unique solution. Peng-Hu-Zhang [10] and Chen-Peng-Zhou [11] proposed some iterative methods to compute the symmetric solutions and optimal approximate symmetric solution of Equation (1.3). The (least square) solution and the optimal approximate (least square) solution of Equation (1.3), which is constrained as bisymmetric, reflexive, generalized reflexive, generalized centro-symmetric, were studied in [11] - [17] . Nevertheless, to the best of our knowledge, the optimal approximate solution of Equation (1.3), which is constrained as symmetric positive semidefinite, (i.e. Problem I) has not been solved. The difficulty of Problem I lies in how to characterize the convex set. In this paper, we first divided the set into three sets and then adopt alternating projections to overcome the difficulty.

Dykstra’s alternating projection algorithm was proposed by Dykstra [18] to treat the problem of finding the projection of a given point onto the intersection of some closed convex sets. It is based on a clear modification of the classical alternating projection algorithm first proposed by Von Neumann [19] , and studied later by Cheney and Goldstein [20] . For an application of Dykstra’s alternating projection algorithm to compute the nearest diagonally dominant matrix see [21] . For a complete survey on Dykstra’s alternation projection algorithm and applications see Deutsch [22] .

In this paper, we propose a new algorithm to compute the optimal approximate symmetric positive semidefinite solution of Equation (1.3). We state Problem I as the minimization of a convex quadratic function over the intersection of three closed convex sets in the vector space From this point of view, Problem I can be solved by the Dykstra’s alternating projection algorithm. If we choose the initial iterative matrix the least Frobenius norm symmetric positive semidefinite solution of the matrix equations is obtained. In the end, we use a numerical example to show that the new algorithm is feasible and effective.

2. Dykstra’s Algorithm for Solving Problem I

In this section, we apply Dykstra’s alternating projection algorithm to compute the optimal approximate symmetric positive semidefinite solution of Equation (1.3). We first introduce Dykstra’s alternating projection algorithm and its convergence theorem.

In order to find the projection of a given point onto the intersection of a finite number of closed convex sets Dykstra [18] proposed Dykstra’s alternating projection algorithm which can be stated as follows. This algorithm can be also seen in [1] [23] - [25] .

Dykstra’s Algorithm 2.1

1) Given the initial value;

2) Set

3) For

For

,

End

End

The utility of Dykstra’s algorithm 2.1 is based on the following theorem (see [23] - [25] and the references therein).

Lemma 2.1. ( [23] , Theorem 2) Let be closed convex subsets of a real Hilbert space H such that For any and any the sequences generated by Dykstra’s algorithm 2.1 converge to that is,

Now we begin to use Dykstra’s algorithm 2.1 to solve Problem I. Firstly, we define three sets

It is easy to know that and if the set is nonempty, then

(2.1)

On the other hand, it is easy to verify that and are closed convex subsets of the real Hilbert space.

After defining the sets and, Problem I can be rewritten as finding such that

(2.2)

By Definition 1.1 and noting that the equalities (2.2) and (1.2), it is easy to find that

(2.3)

Therefore, Problem I can be converted equivalently into finding the projection. Now we will use Dykstra’s algorithm 2.1 to compute the projection. By (2.3), we can get the optimal approximate symmetric positive semidefinite solution of the matrix equations (1.3).

We can see that the key problems to realize Dykstra’s algorithm 2.1 are how to compute the projections, and of a matrix Z onto and, respectively. Such problems are perfectly solvable in the following theorems.

Theorem 2.1. Suppose that the set is nonempty. For a given matrix Z, we have

Proof. By Definition 1.1, we know that the projection is the solution of the following minimization problem

(2.4)

Now we begin to solve the minimization problem (2.4). We first characterize the solution set and then find such that (2.4) holds. Noting that the set is a closed convex set, then the minimization problem (2.4) has a unique solution. Hence The singular value decomposition of the matrices A and B are given by

(2.5)

where are orthogonal matrices, , , , and are orthogonal matrices,. According to the definition of the Moore-Penrose generalized inverse of a matrix, we have

(2.6)

and

(2.7)

Substituting (2.5) into the matrix equation we obtain

which implies

Let

Then the matrix equation can be equivalently written as

which implies that

(2.8)

(2.9)

(2.10)

(2.11)

By (2.8) we have

Noting that the set is nonempty, by (2.5) it is easy to verify that (2.9), (2.10) and (2.11) are identical equations. Hence the general solutions of the matrix equation can be expressed as

(2.12)

where are arbitrary, which implies that the entries of the set can be stated as (2.12).

Consequently,

(2.13)

By (2.13) we know that if and only if

Therefore, the solution of the minimization problem (2.4) is

(2.14)

Combining (2.14) and (2.5)-(2.7), we have

The theorem is proved.

Theorem 2.2. Suppose that the set is nonempty. For a given matrix Z, we have

Proof. The proof is similar to that of Theorem 2.1 and is omitted here.

For any it is easy to verify that is a symmetric matrix. Then the spectral decomposition of the matrix E is

where and Then by Theorem 2.1 of Higham [26] and Definition 1.1, we have

Theorem 2.3. For a given matrix Z, we have

where

By Dykstra’s algorithm 2.1 and noting that the projection and in Theorems 2.1, 2.2 and 2.3, we get a new algorithm to compute the optimal approximate symmetric positive semidefinite solution of the matrix equations (1.3) which can be stated as follows.

Algorithm 2.2

1) Set the initial value

2) Set

3) For

For

,

End

End

By Lemma 2.1 and (2.1), and noting that and are closed convex sets, we get the convergence theorem for Algorithm 2.2.

Theorem 2.4. If the set is nonempty, then the matrix sequences and generated by Algorithm 2.2 converge to the projection that is

Combining Theorem 2.4 and the equalities (2.3) and (2.2), we have

Theorem 2.5. If the set is nonempty, then the matrix sequences and generated by Algorithm 2.2 converge to optimal approximate symmetric positive semidefinite solution of the matrix equations (1.3). Moreover, if the initial matrix then the matrix sequences and converge to the least Frobenius norm symmetric positive semidefinite solution of the matrix equations

3. Numerical Experiments

In this section, we give a numerical example to illustrate that the new algorithm is feasible and effective to compute the optimal approximate symmetric positive semidefinite solution of the matrix equation (1.3). All programs are written in M ATLAB 7.8. We denote

and use the practical stopping criterion.

Example 3.1. Consider the matrix equation (1.3) with

Here we use and to stand for matrix of ones and zeros. It is easy to verify that is a solution of the matrix equations (1.4), that is to say, the set is nonempty. Therefore we can use Algorithm 2.2 to compute the optimal symmetric positive semidefinite solution of the matrix equation (1.3).

1) Let After 41 iterations of Algorithm 2.2, we get the optimal approximate symmetric positive semidefinite solution

and its residual error

By concrete computations, we know that the distance from to the solution set is

2) Let After 88 iterations of Algorithm 2.2, we get the optimal approximate symmetric positive semidefinite solution

and its residual error

By concrete computations, we know that the distance from to the solution set is

3) Let After 116 iterations of Algorithm 2.2, we get the optimal approximate solution

which is also the least Frobenius norm symmetric positive semidefinite solution of the matrix equations (1.3), and its residual error

By concrete computations, we know that the distance from to the solution set is

Example 4.1 shows that Algorithm 2.2 is feasible and effective to compute the optimal approximate symmetric positive semidefinite solution of the matrix equations (1.3).

4. Conclusion

In this paper, we state Problem I as the minimization of a convex quadratic function over the intersection of three closed convex sets in the Hilbert space, then we can use Dykstra’s alternating projection algorithm to compute the optimal approximate symmetric positive semidefinite solution of the matrix equations (1.3). If we choose the initial matrix the least Frobenius norm symmetric positive semidefinite solution of the matrix equations (1.3) can be obtained. A numerical example show that the new algorithm is feasible and effec- tive to compute the optimal approximate symmetric positive semidefinite solution of the matrix equations (1.3).

Cite this paper

ChunmeiLi,XuefengDuan,ZhulingJiang, (2016) Dykstra’s Algorithm for the Optimal Approximate Symmetric Positive Semidefinite Solution of a Class of Matrix Equations. Advances in Linear Algebra & Matrix Theory,06,1-10. doi: 10.4236/alamt.2016.61001

References

NOTES

^*The work was supported by National Natural Science Foundation of China (No.11561015; 11261014; 11301107), Natural Science Foundation of Guangxi Province (No.2012GXNSFBA053006; 2013GXNSFBA019009).

^#Corresponding author.