Received 23 July 2015; accepted 16 November 2015; published 19 November 2015

ABSTRACT

We study decomposition of finite Abelian groups into subsets and show by examples a negative answer to the question of whether Hajós-property is inherited by direct product of groups which have Hajós-property.

Keywords:

Abelian Groups, Hajós-Property, Factorization of Abelian Groups

1. Introduction

The general setting is as follows: Suppose we decompose a group G into direct product of subsets 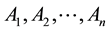of G in such a way that each element g in G has a unique representation of the form 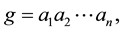where. The question then asked is what we can say about the subsets.

The answer is rather difficult even if we do not impose many restrictions either on G or on the subsets. The most important special case has some connection with a group-theoretial formulation by G. Hajós [1] of a conjecture by H. Minkowski [2] ; this is when G is a finite Abelian group and each of the subsets is of the form

,

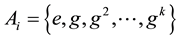where 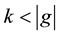is an integer; here e denotes the identity element of g and 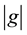denotes order of the element g of G. Then a result due to Hajos states that one of the subsets 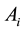must be a subgroup of G. L. Rédei [3] generalizes this result to the case when the condition on the subsets is that they contain a prime number of elements.

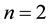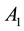Another interesting question has also been asked by Hajos. It is concerned with the case in which G is an Abelian group and; the question then asked is as follows: Suppose G has a decomposition as. Does it follow that one of the subsets or 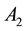is a direct product of another subset and a proper subgroup of G?

The concept of Hajós factorization begin group-theoretical but now finds applications in diverse fields such as number theory, [4] coding theory [5] and even in music [6] .

2. Preliminaries

Throughout this paper, G will denote a finite Abelian group, e the identity of G, and if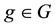, then 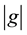will denote its order. We will also use to denote the number of elements of a subset A of G. A subset A of G of the form is called a cyclic subset of G; here k is an integer with. If

we say that we have a factorization of G. If in addition, each of the subsets contains e, we say that we have a normalized factorization of G. A subset A of G is called periodic if there exists, such that. Such an element if it exists is called a period for A. A group G is said to be of type, if it is a direct product of cyclic groups of orders, (where of course are primes and are non-negative integers).

3. Remarks

1) If is a factorization of G , then for any, is also a factorization of G. Similarly, with. Thus, we may assume that all factorization we consider are normalized.

2) In the literature, a group G is said to be "good" if from each factorization, it follows that one the subsets A or B is periodic.

We extend the above definition as follows.

4. Definition

A group G has the Hajos-n-property or n-good if from any factorization

it follows that one of the subsets is periodic. Otherwise it is n-bad. We will also say G is totally- good if it is n-good for all possible values of n.

The following results are known and will be used in this paper.

Lemma 1 [7]

If G is of type, then G is 2-good.

Lemma 2 [8]

A cyclic group G of order, where is prime is totally-good.

Lemma 3 [8]

If G is of type, where and is prime, then G is n-bad for all n,.

Lemma 4 [9]

If H is a proper subgroup of G, then there exists a non-periodic set N such that is a factorization of G, except when H is a subgroup of index 2 in an elementary abelian 2-group.

Lemma 5 [7]

If A and B are non-periodic subsets o a group G and A is contained in a subgroup H of G such that is a factorization of G, then AB is also non-periodic.

5. Results

Theorem 6

If G is of type , then G is totally-good.

Proof.

Let be a factorization of G.

Now, the possible values for n are 1, 2, 3 and 4.

The case is trivial.

The case follows from Lemma 1.

The case follows from Rédei’s theorem.

So, we only need details the case. So now,.

We may assume. Now, is also a factorization of G. Hence by Lemma 1, either is or is periodic. If is periodic, we are done. So assume is periodic, say with period. We may assume.

Let and. Then. If, then is a subgroup and hence periodic, while if, then is a subgroup and hence periodic. Suppose, then we must have either 1) and both of which give, which is impossible; or 2) and both of which imply that both and are subgroups of G. This ends the proof. ,

Theorem 7

If G is of type, then G is 3-bad.

Proof.

Let, where and.

Let, and.

Then is a factorization of G and none of the subsets, or is periodic. This ends the proof. ,

Theorem 8

Let H be a proper subgroup of a group G. If H is n-bad, then G is both n and -bad.

Proof.

Since H is n-bad, there is a factorization of H, where none of the subsets is periodic. Now, by Lemma 5, there is a factorization of G, with nonperiodic. Hence,

is a factorization G with none none of the subsets periodic. Thus, G is -bad.

Also, is a factorization G with none of the subsets periodic. Here, the non- periodicity of the factor follows from Lemma 5. This ends the proof. ,

Theorem 9

If G is of type, where, , then G is both 3 and 4-bad.

Proof.

G has a subgroup H of type which is 3-bad by Theorem 7.

So, the result follows from Theorem 8. This ends the proof.

Finally, we show by example what we aimed to show.

6. Example 1

Let be of type. Then by Lemma 1, is 2-good. Now, consider the group and note that G is of type Observe that G has a subgroup H of type which is 3-bad by Theorem 9. Now, by Lemma 4, G has a factorization, where N is nonperiodic. Hence, G has a factorization, where none of the factor is periodic. Thus G is 4-bad. This ends the proof. ,

7. Example 2

Let be of type and be of type, where and are positive integers and is prime. Then by Lemma 2, is m-good for all m, , and is n-good for all m,. Consider the group. Then by Lemma 3, is -bad for all,. This ends the proof. ,

Cite this paper

KhalidAmin, (2015) Hajós-Property for Direct Product of Groups. Advances in Linear Algebra & Matrix Theory,05,139-142. doi: 10.4236/alamt.2015.54013

References