Received 24 March 2015; accepted 6 June 2015; published 9 June 2015

ABSTRACT

One of the most important properties of M-matrices is element-wise non-negative of its inverse. In this paper, we consider element-wise perturbations of tridiagonal M-matrices and obtain bounds on the perturbations so that the non-negative inverse persists. The largest interval is given by which the diagonal entries of the inverse of tridiagonal M-matrices can be perturbed without losing the property of total nonnegativity. A numerical example is given to illustrate our findings.

Keywords:

Totally Positive Matrix, Totally Nonnegative Matrix, Tridiagonal Matrices, Compound Matrix, Element-Wise Perturbations

1. Introduction

In many mathematical problems, -matrices and 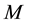-matrices play an important role. It is often useful to know the properties of their inverses, especially when the -matrices and the M-matrices have a special combinatorial structure, for more details we refer the reader [1] . M-matrices have important applications, for instance, in iterative methods, in numerical analysis, in the analysis of dynamical systems, in economics, and in mathematical programming. One of the most important properties of some kinds of M-matrices is the nonegativity of their inverses, which plays central role in many of mathematical problems.

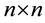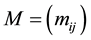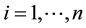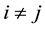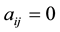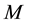An real matrix is called M-matrix if, and, , over the years, M-matrices have considerable attention, in large part because they arise in many applications [2] [3] . Recently, a noticeable amount of attention has turned to the inverse of tridiagonal M-matrices (those matrices which happen to be inverses of special form of M-matrices with property whenever) and is generalized strictly diagonally dominant. A matrix is said to be generalized (strictly) diagonally dominant

if. Of particular importance to us is the fact that since 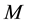is an M-matrix it is non-singular and

>0where the inequality is satisfied element-wise. A rich class of M-matrices were introduced by Ostrowski in 1937 [4] , with reference to the work of Minkowski [5] [6] . A condition which is easy to check is that a matrix 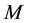is an M-matrix if and only if, and, and is generalized strictly diagonally dominant.

In this paper, we consider the inverse of perturbed M-matrix. Specifically we consider the effect of changing single elements inside the diagonal of. We are interested in the large amount by which the single diagonal element of can be varied without losing the property of total nonnegativity.

The reminder of the paper is organized as follows. In section 2, we explain our notations and some needed important definitions are presented. In section 3, some auxiliary results and important prepositions and lemmas are stated. In section 4, we present our results.

2. Notations

In this section we introduce the notation that will be used in developing the paper. For we denote by the set of all strictly increasing sequences of integers chosen from. For, , we denote by the submatrix of contained in the rows indexed by and columns indexed by. A matrix is called totally positive (abbreviated TP henceforth) if and totally nonnegative (abbreviated TN) if for all,. For a given index, with property, , the dispersion of,

denoted by, is defined to be.

Throughout this paper we use the following notation for general tridiagonal M-matrix:

where, and, and each is large enough that is strictly diagonally dominant.

We let to be the square standard basis matrix whose only nonzero entry is 1 that occurs in the position.

Definition 2.1 Compound Matrices ([7] , p. 19).

Let be a square matrix of order. Let be the index set of cardinality, defining, are the index sets of cardinality.

Construct the following table which depends on.

The created matrix

is called, compound matrix of.

For example, if

with indexed sets, and.

Then.

3. Auxiliary Results

We start with some basic facts on tridiagonal M-matrices. We can find the determinant of any tridiagonal M-matrix by using the following recursion equation [8] [9] .

And we have the following proposition for finding the determinant of a tridiagonal M-matrix.

Proposition 3.1 ([10] , formula 4.1) For any tridiagonal M-matrix the following relation is true

.

We will present now some of propositions of nonsingular totally nonnegative matrices which important for our work.

Proposition 3.2 [10] [11]

For any nonsingular totally nonnegative matrix, all principle minors are positive.

That is, for all and.

Proposition 3.3 ([7] , p. 21)

Let M be a nonsingular tridiagonal M-matrix, and be the inverse of the matrix M then

, when.

In the sequel we will make use the following lemma, see, e.g. [12] .

Lemma 3.4 (Sylvester Identity)

Partition square matrix of order n, , as:

,

where square matrix of order and, , and are scalars.

Define the submatrices

If is nonsingular, then

Lemma 3.5 ([11] , p.199) Let be a square matrix of order, with. Then

is totally nonnegative.

We now state an important result which links the determinant of M-matrix with the value of the elements of its inverse.

Lemma 3.6 [10] Let be a tridiagonal matrix of order n, then we can find the elements of in-

verse matrix by using the following formula

.

4. Main Results

In this section, we present our results based on the inverse of tridiagonal M-matrices. Firstly we begin with the following theorem.

Theorem 4.1

Let be strictly diagonally dominant M-matrix.

If is the compound matrix of M then the matrix is totally nonnega-

tive matrix. Moreover, where

Proof: Let be strictly diagonally dominant M-matrix.

Then is totally nonnegative matrix. So is.

You can find this formula in ([7] , p. 21).

There is an explicit formula for the determinant of given as

Multiply the first row by and add it to the row to obtain

where,

And now apply an induction argument to get the result.

Numerical Example: Let be strictly diagonally dominant M-matrix, then

and is totally nonnegative.

Note that and

Numerically we can conclude the following fact.

Fact: For any tridiagonal M-matrix the following formula is true.

for

Moreover,

To prove this result we use Theorem 4.1.

Suppose M is nonsingular then, so

For example, when, the M-matrix of our form

has an inverse given as

Similarly we can find.

Illustrative Example: Let be a tridiagonal M-matrix and

Note that

Observe that the error came from the rounded to the nearest part of 10,000.

Theorem 4.2 Let M be a strictly diagonally dominant M-matrix, if, , then

Proof:

Assume and

, , ,.

Note that by previous fact, and by using Sylvester's identity, we have

Moreover we conclude the following theorem.

Theorem 4.3 Let M be the M-matrix defined above then

For example

,

Let then

and

Now, we will perturb elements inside the diagonal band of the inverse of M-matrix without losing the nonnegativity property. We begin with the element then generalize to other elements.

Theorem 4.4 Let M be a strictly diagonally dominant tridiagonal -matrix. Then the matrix

is totally nonnegative for all.

Proof:

Let

Be a nonsingular strictly diagonally dominant tridiagonal M-matrix then is totally nonnegative.

By Lemma 3.5 and Proposition 3.2, we have

is totally nonnegative.

By using the formula in Proposition 3.3

.

Note that a similar result holds for decreasing the element by considering the matrix, which reverses the matrix as the relation.

We can generalize this result for the other elements of diagonal.

Theorem 4.5 Assume M is a strictly diagonally dominant tridiagonal M-matrix. Then the matrix

is totally nonnegative for all.

Proof: Suppose that is not totally nonnegative for all, then there exist

both contain such that.

To compute expand the determinant along the row of then

where, , and is some minor of.

Take the case when odd. Thus, is a positive linear compination of minors of and hence is positive, which contradicts the assumption.

Now suppose such that is totally nonnegative matrix.

Suppose that, then by Theorem 4.3.

, since

which contradicts the nonnegativity of.

Numerical Example: Let is strictly diagonally dominant tridiagonal M-matrix

so

The matrices

, ,

, ,

, , and

,.

are TNN matrices.

Note that.

References