Advances in Linear Algebra & Matrix Theory
Vol.05 No.01(2015), Article ID:53902,14 pages
10.4236/alamt.2015.51001
New Approach for the Inversion of Structured Matrices via Newton’s Iteration
Mohammad M. Tabanjeh
Department of Mathematics and Computer Science, Virginia State University, Petersburg, VA, USA
Email: mtabanjeh@vsu.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 January 2015; accepted 5 February 2015; published 10 February 2015
ABSTRACT
Newton’s iteration is a fundamental tool for numerical solutions of systems of equations. The well-known iteration  rapidly refines a crude initial approximation
rapidly refines a crude initial approximation 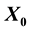 to the inverse of a general nonsingular matrix. In this paper, we will extend and apply this me- thod to
to the inverse of a general nonsingular matrix. In this paper, we will extend and apply this me- thod to 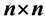 structured matrices
structured matrices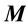 , in which matrix multiplication has a lower computational cost. These matrices can be represented by their short generators which allow faster compu- tations based on the displacement operators tool. However, the length of the generators is tend to grow and the iterations do not preserve matrix structure. So, the main goal is to control the grow- th of the length of the short displacement generators so that we can operate with matrices of low rank and carry out the computations much faster. In order to achieve our goal, we will compress the computed approximations to the inverse to yield a superfast algorithm. We will describe two different compression techniques based on the SVD and substitution and we will analyze these approaches. Our main algorithm can be applied to more general classes of structured matrices.
, in which matrix multiplication has a lower computational cost. These matrices can be represented by their short generators which allow faster compu- tations based on the displacement operators tool. However, the length of the generators is tend to grow and the iterations do not preserve matrix structure. So, the main goal is to control the grow- th of the length of the short displacement generators so that we can operate with matrices of low rank and carry out the computations much faster. In order to achieve our goal, we will compress the computed approximations to the inverse to yield a superfast algorithm. We will describe two different compression techniques based on the SVD and substitution and we will analyze these approaches. Our main algorithm can be applied to more general classes of structured matrices.
Keywords:
Newton Iteration, Structured Matrices, Superfast Algorithm, Displacement Operators, Matrix Inverse.

1. Introduction
Frequently, matrices encountered in practical computations that have some special structures which can be exploited to simplify the computations. In particular, computations with dense structured matrices are ubiquitous in sciences, communications and engineering. Exploitation of structure enables dramatic acceleration of the computations and a major decrease in memory space, but sometimes it also leads to numerical stability problems. The best-known classes of structured matrices are Toeplitz and Hankel matrices, but Cauchy and Vandermonde types are also quite popular. The computations with such matrices are widely applied in the areas of algebraic coding, control, signal processing, solution of partial differential equations and algebraic computing. For ex- ample, Toeplitz matrices arise in some major signal processing computations and Cauchy matrices appear in the study of integral equations and conformal mappings. The complexity of computations with 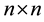 dense structured matrices dramatically decreases in comparison with the general
dense structured matrices dramatically decreases in comparison with the general 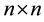 matrices, that is, from the order of
matrices, that is, from the order of  words of storage space and
words of storage space and  arithmetic operations (ops) with
arithmetic operations (ops) with 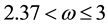 in the best algorithms, to
in the best algorithms, to  words of storage space and to
words of storage space and to  ops (and sometimes to
ops (and sometimes to  ops) (Table 1). The displacement rank
ops) (Table 1). The displacement rank 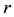 for an
for an 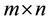 Toeplitz and Hankel matrix is at most 2. A matrix is Toeplitz-like or Hankel-like if
Toeplitz and Hankel matrix is at most 2. A matrix is Toeplitz-like or Hankel-like if  is small or bounded by a small constant independent of
is small or bounded by a small constant independent of 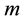 and
and![]() . Those matrices can be represented by
. Those matrices can be represented by ![]() entries of its short displacement generators instead of
entries of its short displacement generators instead of ![]() entries which leads to more efficient storage of the entries in computer memory and much faster computations [1] . In this paper, we will focus our study on Newton’s iteration for computing the inverse of a structured matrix and we will analyze the resulting algorithms. This iteration is well-known for its numerically stability and faster convergence. Newton’s iteration
entries which leads to more efficient storage of the entries in computer memory and much faster computations [1] . In this paper, we will focus our study on Newton’s iteration for computing the inverse of a structured matrix and we will analyze the resulting algorithms. This iteration is well-known for its numerically stability and faster convergence. Newton’s iteration
![]() (1)
(1)
for matrix inversion was initially proposed by Schultz in 1933 and studied by Pan and others. The authors of [2] described quadratically convergent algorithms for the refinement of rough initial approximations to the inverse of Toeplitz and Toeplitz-like matrices and to the solutions of Toeplitz and Toeplitz linear systems of equations. The algorithms are based on the inversion formulas for Toeplitz matrices. The Cauchy-like case was studied in [3] . Since those matrices can be represented by their short generators, which allow faster com- putations based on the displacement operators tool, we can employ Newton’s iteration to compute the inverse of the input structured matrices. However, Newton’s iteration destroys the structure of the structured matrices when used. Therefore, in Section 5 we will study two compression techniques in details, namely, truncation of the smallest singular values of the displacement and the substitution of approximate inverses for the inverse matrix into its displacement expression to preserve the structure. Finally, each iteration step is reduced to two multiplications of structured matrices and each iteration is performed by using nearly linear time and optimal memory space which leads to superfast algorithm, especially if the input matrix is a well-conditioned structured matrix. Our main algorithm of Section 6 can be applied to more general classes of structured matrices. We will support our analysis with numerical experiments with Toeplitz matrices in Section 7.
2. Definition of Structured Matrices
Definition 1 A matrix ![]() is a Toeplitz matrix if
is a Toeplitz matrix if ![]() for every pair of its entries
for every pair of its entries ![]() and
and
![]() . A matrix
. A matrix ![]() is a Hankel matrix if
is a Hankel matrix if ![]() for every pair of its entries
for every pair of its entries ![]() and
and
![]() . For a given vector
. For a given vector![]() , the matrix
, the matrix ![]() of the form
of the form ![]() is called a Vander-
is called a Vander-
monde matrix. Given two vectors s and t such that ![]() for all i and
for all i and![]() , the
, the ![]() matrix
matrix ![]()
is a Cauchy (generalized Hilbert) matrix where![]() .
.
Example 1![]() ,
, ![]() ,
, ![]() , and
, and ![]()
are ![]() Teoplitz, Hankel, Vandermonde, and Cauchy matrices respectively that can be represented by the 5-dim vector
Teoplitz, Hankel, Vandermonde, and Cauchy matrices respectively that can be represented by the 5-dim vector![]() , the 5-dim vector
, the 5-dim vector![]() , the 3-dim vector
, the 3-dim vector![]() , and the 3- dim vectors
, and the 3- dim vectors ![]() and
and ![]() respectively.
respectively.
We refer the reader to [4] and [5] for more details on the basic properties and features of structured matrices.
3. Displacement Representation of Structured Matrices
The concept of displacement operators and displacement rank, initially introduced by Kailath, Kung, and Morf in 1979, and studied by other authors such as Bini and Pan, is a powerful tool for dealing with matrices with structure. The displacement rank approach was intended for more restricted use when it was initially introduced in [6] (also [7] ), namely, to measure how “close” to Toeplitz a given matrix is. Then the idea turned out to be even deeper and more powerful, thus it was developed, generalized and extended to other structured matrices. In this paper, we consider the most general and modern interpretation of the displacement of a matrix ![]() (see Definition 2). The main idea is, for a given structured matrix
(see Definition 2). The main idea is, for a given structured matrix![]() , we need to find an operator
, we need to find an operator ![]() that transforms the matrix
that transforms the matrix ![]() into a low rank matrix
into a low rank matrix![]() , such that one can easily recover
, such that one can easily recover ![]() from its image
from its image ![]() and operate with low rank matrices instead. Such operators that shift and scale the entries of the structured matrices turn out to be appropriate tools for introducing and defining the matrices of Toeplitz-like, Hankel-like, Vandermonde-like, and Cauchy-like types which we will introduce in Definition 4.
and operate with low rank matrices instead. Such operators that shift and scale the entries of the structured matrices turn out to be appropriate tools for introducing and defining the matrices of Toeplitz-like, Hankel-like, Vandermonde-like, and Cauchy-like types which we will introduce in Definition 4.
Definition 2 For any fixed field ![]() (say the complex field
(say the complex field![]() ) and a fixed pair
) and a fixed pair ![]() of operator matrices, we define the linear displacement operators
of operator matrices, we define the linear displacement operators ![]() of Sylvester type
of Sylvester type![]() :
:
![]() (2)
(2)
and Stein type![]() :
:
![]() . (3)
. (3)
The image ![]() of the operator
of the operator ![]() is called the displacement of the matrix
is called the displacement of the matrix![]() . The operators of Sylvester and Stein types can be transformed easily into one another if at least one of the two associated operator matrices is nonsingular. This leads to the following theorem.
. The operators of Sylvester and Stein types can be transformed easily into one another if at least one of the two associated operator matrices is nonsingular. This leads to the following theorem.
Theorem 1 ![]() if the operator matrix
if the operator matrix ![]() is nonsingular, and
is nonsingular, and ![]() if the
if the
operator matrix ![]() is nonsingular.
is nonsingular.
Proof.![]() , and
, and
![]() .
.
The operator matrices that we will use are the unit f-circulant matrix
![]() , and the diagonal matrix
, and the diagonal matrix![]() . Note that
. Note that
![]() is unit lower triangular Toeplitz matrix.
is unit lower triangular Toeplitz matrix.
![]() is an f-circulant for a vector
is an f-circulant for a vector![]() . For example,
. For example,
![]() is a lower triangular matrix.
is a lower triangular matrix.
![]()
Table 1. Parameters and flops (floating point arithmetic operations) count.
Example 2 (Toeplitz Matrices). Let![]() . Then if we apply the displacement operator of Sylvester
. Then if we apply the displacement operator of Sylvester
type (2) to Toeplitz matrix ![]() using the shift operator matrices
using the shift operator matrices ![]() and
and![]() , we will get:
, we will get:
![]() .
.
This operator displaces the entries of the matrix ![]() so that the image can be represented by the first row and the last column. Furthermore, the image is a rank
so that the image can be represented by the first row and the last column. Furthermore, the image is a rank ![]() matrix
matrix
Notice that the operator matrices vary depending on the structure of the matrix![]() . We use shift operator matrices (such as
. We use shift operator matrices (such as ![]() and
and ![]() for any scalar
for any scalar![]() ) for the structures of Toeplitz and Hankel type, scaling operator matrices (such as
) for the structures of Toeplitz and Hankel type, scaling operator matrices (such as![]() ) for the Cauchy structure, and shift and scaling operator matrices for the structure of Vandermonde type. One can restrict the choices of
) for the Cauchy structure, and shift and scaling operator matrices for the structure of Vandermonde type. One can restrict the choices of ![]() to 0 and 1. However, other operator matrices may be used with other matrix structures (see Table 2).
to 0 and 1. However, other operator matrices may be used with other matrix structures (see Table 2).
Definition 3 For an ![]() structured matrix
structured matrix ![]() and an associated operator
and an associated operator![]() , or
, or![]() , the number
, the number ![]() is called the
is called the ![]() -rank or the displacement rank of the matrix
-rank or the displacement rank of the matrix![]() .
.
The constant ![]() in Definition 3 usually remains relatively small as the size of
in Definition 3 usually remains relatively small as the size of ![]() grows large, that is,
grows large, that is, ![]() is
is
small relative to![]() , say
, say ![]() or
or ![]() as
as ![]() and
and ![]() grow large. In this case, we
grow large. In this case, we
call the matrix ![]() -like and having structure of type
-like and having structure of type![]() . Now let us recall the linear operators
. Now let us recall the linear operators ![]() of (2) and (3) that map a matrix
of (2) and (3) that map a matrix ![]() into its displacements:
into its displacements:
![]() (4)
(4)
and
![]() (5)
(5)
where ![]() and
and ![]() are operator matrices of Table 2,
are operator matrices of Table 2, ![]() and
and ![]() are
are ![]() ma- trices. Then the matrix pair
ma- trices. Then the matrix pair ![]() is called a (nonunique)
is called a (nonunique) ![]() -generator (or displacement generator) of length
-generator (or displacement generator) of length ![]() for
for![]() ,
, ![]() (the
(the ![]() -rank or the displacement rank of
-rank or the displacement rank of![]() ). If
). If ![]() is an
is an ![]() matrix and
matrix and ![]() is small relative to
is small relative to ![]() and
and![]() , then
, then ![]() is said to have
is said to have ![]() -structure or to be an
-structure or to be an ![]() -structured matrix. The displacement
-structured matrix. The displacement ![]() (as a matrix of small rank) can be represented with a short generator defined by only a small number of parameters. For instance, the singular value decomposition (SVD) of the matrix
(as a matrix of small rank) can be represented with a short generator defined by only a small number of parameters. For instance, the singular value decomposition (SVD) of the matrix ![]() of size
of size ![]() gives us its orthogonal generator that consists of two generator matrices
gives us its orthogonal generator that consists of two generator matrices ![]() and
and ![]() having orthogonal columns and of sizes
having orthogonal columns and of sizes ![]() and
and ![]() respectively, that is a total of
respectively, that is a total of ![]() entries. The matrix pair
entries. The matrix pair ![]() is called an
is called an ![]() -generator (or displacement generator) of length
-generator (or displacement generator) of length ![]() for
for![]() . It is also a generator of length
. It is also a generator of length ![]() for
for![]() . Note that the pair
. Note that the pair ![]() is nonunique for a fixed
is nonunique for a fixed![]() . In particular, for Toeplitz, Hankel, Vandermonde, and Cauchy matrices, the length
. In particular, for Toeplitz, Hankel, Vandermonde, and Cauchy matrices, the length ![]() of the associated generators (4) and (5) is as small as 1 or 2 for some appropriate choices of the operator matrices
of the associated generators (4) and (5) is as small as 1 or 2 for some appropriate choices of the operator matrices ![]() and
and ![]() of Table 2. The four classes of structured matrices are naturally extended to Toeplitz-like, Hankel-like, Vandermonde-like, and Cauchy- like matrices, for which
of Table 2. The four classes of structured matrices are naturally extended to Toeplitz-like, Hankel-like, Vandermonde-like, and Cauchy- like matrices, for which ![]() is bounded by a fixed (not too large) constant.
is bounded by a fixed (not too large) constant.
Definition 4 An ![]() matrix
matrix ![]() is Toeplitz-like if
is Toeplitz-like if ![]() is small relative to
is small relative to ![]() and if
and if
![]()
Table 2. Operator Matrices for ![]() and
and![]() .
.
![]() is given with its
is given with its ![]() -generator of length
-generator of length![]() , where
, where![]() ,
, ![]() ,
, ![]() , and
, and
![]() for a fixed pair of scalars
for a fixed pair of scalars ![]() and
and![]() . A matrix
. A matrix ![]() is Hankel-like if
is Hankel-like if ![]() or
or ![]() is Toeplitz-
is Toeplitz-
like where ![]() is the reflection matrix.
is the reflection matrix.
Therefore, the problems of solving Toeplitz-like and Hankel-like linear systems are reduced to each other.
Remark 1 In the case where the operator ![]() is associated with Toeplitz, Hankel, Vandermonde, or Cauchy matrices
is associated with Toeplitz, Hankel, Vandermonde, or Cauchy matrices![]() , we call an
, we call an ![]() -like matrix Toeplitz-like, Hankel-like, Vandermonde-like, or Cauchy-like matrix, respectively, and we say that the matrix has the structure of Toeplitz, Hankel, Vandermonde, or Cauchy type respectively. To take advantage of the matrix structure, we are going to COMPRESS the structured input matrix
-like matrix Toeplitz-like, Hankel-like, Vandermonde-like, or Cauchy-like matrix, respectively, and we say that the matrix has the structure of Toeplitz, Hankel, Vandermonde, or Cauchy type respectively. To take advantage of the matrix structure, we are going to COMPRESS the structured input matrix ![]() via its short L-generators based on Theorem 2 below, then we will OPERATE with L-generators rather than with the matrix itself, and finally RECOVER the output from the computed short L-generators.
via its short L-generators based on Theorem 2 below, then we will OPERATE with L-generators rather than with the matrix itself, and finally RECOVER the output from the computed short L-generators.
Definition 5 A linear operator ![]() is nonsingular if the matrix equation
is nonsingular if the matrix equation ![]() implies that
implies that![]() .
.
Definition 6 We define the norm of a nonsingular linear operator ![]() and its inverse
and its inverse ![]() as follows:
as follows:
![]() and
and![]() , for
, for![]() , or
, or![]() , and where
, and where
the supremum is taken over all matrices ![]() having a positive
having a positive ![]() -rank of at most
-rank of at most![]() . In this case the condition
. In this case the condition
number ![]() of the operator
of the operator ![]() is defined as
is defined as ![]()
Theorem 2 [8] Let ![]() and
and ![]() be a pair of
be a pair of ![]() matrices,
matrices, ![]() and
and![]() , where
, where ![]() and
and ![]() denote the
denote the ![]() -th columns of
-th columns of ![]() and
and ![]() respectively. Let
respectively. Let![]() . Then we have one of
. Then we have one of
the following Toeplitz type matrices:![]() , where
, where![]() ,
,![]() .
.
![]() , where
, where![]() ,
,![]() .
.![]() , where
, where![]() ,
,![]() .
.![]() , where
, where![]() ,
,![]() .
.
Theorem 3 Let M be a nonsingular matrix, then we have the following:
1)![]() .
.
2)![]() , if
, if ![]() is a nonsingular matrix.
is a nonsingular matrix.
3)![]() , if
, if ![]() is a nonsingular matrix.
is a nonsingular matrix.
Proof.
1) ![]()
![]()
2) ![]()
![]()
3) ![]()
![]()
Theorem 4 Let a pair of ![]() matrices G and
matrices G and ![]() form a
form a ![]() -generator of length
-generator of length ![]() for a nonsingular matrix
for a nonsingular matrix![]() . Write
. Write ![]() and
and![]() . Then
. Then![]() .
.
Proof. By Theorem 3, ![]() , where
, where ![]() and
and![]() .
. ![]()
4. Newton’s Iteration for General Matrix Inversion
Given an ![]() nonsingular matrix
nonsingular matrix ![]() and an initial approximation
and an initial approximation ![]() to its inverse
to its inverse ![]() that satisfies the bound
that satisfies the bound ![]() for some positive
for some positive ![]() and some fixed matrix norm, Newton’s iteration (1) can be written in the form
and some fixed matrix norm, Newton’s iteration (1) can be written in the form
![]() (6)
(6)
and rapidly improves the initial approximation ![]() to the inverse.
to the inverse. ![]() can be supplied by either some computational methods such as preconditioning conjugate gradient method or by an exact solution algorithm that requires refinement due to rounding errors.
can be supplied by either some computational methods such as preconditioning conjugate gradient method or by an exact solution algorithm that requires refinement due to rounding errors.
Lemma 1 Newton’s iteration (6) converges quadratically to the inverse of an ![]() nonsingular matrix
nonsingular matrix![]() .
.
Proof. From (6) , since![]() ,
, ![]() , then
, then
![]() . We define the error matrices
. We define the error matrices
![]() ,
, ![]() and the residual matrices
and the residual matrices![]() ,
,![]() . Since
. Since![]() , then
, then
![]() and hence the norm of the residual matrices
and hence the norm of the residual matrices ![]() is bounded above by
is bounded above by![]() . This proves that
. This proves that
Newton’s iteration converges quadratically. ![]()
If ![]() is a given residual norm bound, the bound
is a given residual norm bound, the bound
![]() (7)
(7)
is guaranteed in ![]() recursive steps (6), where
recursive steps (6), where ![]() stands for the smallest integer not exceeded by
stands for the smallest integer not exceeded by![]() . (7) also implies that
. (7) also implies that![]() . Since
. Since![]() , it follows that
, it follows that![]() ,
,
so that the matrix ![]() approximates
approximates ![]() with a relative error norm less than
with a relative error norm less than![]() .
.
Remark 2 Each step of Newton’s iteration (6) involves the multiplication of ![]() by
by![]() , the addition of 2 to all of the diagonal entries of the product, which takes
, the addition of 2 to all of the diagonal entries of the product, which takes ![]() additions, and the pre-multiplication of the resulting matrix by
additions, and the pre-multiplication of the resulting matrix by![]() . The most costly steps are the two matrix multiplications; each step takes
. The most costly steps are the two matrix multiplications; each step takes ![]() multiplications and
multiplications and ![]() additions for a pair of general
additions for a pair of general ![]() input matrices
input matrices ![]() and
and![]() . Of course, this cost will be reduced if the input matrix is structured (see Section 5).
. Of course, this cost will be reduced if the input matrix is structured (see Section 5).
Example 3 (Newton’s iteration versus linear convergent schemes.) Let ![]() and
and![]() . Then by quadratic convergence of Newton’s iteration, we only need 5 iterative steps of (6) to compute
. Then by quadratic convergence of Newton’s iteration, we only need 5 iterative steps of (6) to compute ![]() that satisfies the bound
that satisfies the bound ![]() and hence
and hence![]() . If we consider any linearly convergent scheme such as Jacobi’s or Gauss-Seidels’s iteration ([9] , p. 611) for the same input matrix, the norm of the error matrix of the computed approximation to
. If we consider any linearly convergent scheme such as Jacobi’s or Gauss-Seidels’s iteration ([9] , p. 611) for the same input matrix, the norm of the error matrix of the computed approximation to ![]() decreases by factor 2 in each iteration step. The error norm decreases to below
decreases by factor 2 in each iteration step. The error norm decreases to below ![]() in
in ![]() iteration steps, so this will take 19 iteration steps to ensure the bound (7) for the same
iteration steps, so this will take 19 iteration steps to ensure the bound (7) for the same![]() .
.
5. Newton’s Iteration for Structured Matrix Inversion
5.1. Newton-Structured Iteration
In Section 4, we showed that for a general input matrix![]() , the computational cost of iteration (6) is quite high because matrix products must be computed at every step (see Remark 2). However, for structured matrices
, the computational cost of iteration (6) is quite high because matrix products must be computed at every step (see Remark 2). However, for structured matrices![]() , matrix multiplication has a lower computational cost of
, matrix multiplication has a lower computational cost of ![]() flops for
flops for![]() , provided that we operate with displacement generators of length
, provided that we operate with displacement generators of length ![]() and
and ![]() for the two input matrices
for the two input matrices ![]() and
and ![]() res- pectively. So if
res- pectively. So if ![]() and
and ![]() are structured matrices, say Toeplitz or Toeplitz-like, the computations required for the Newton’s iteration can be carried out more efficiently. In general, for the four classes of structured matrices of Definition 1, we usually associate various linear displacement operators
are structured matrices, say Toeplitz or Toeplitz-like, the computations required for the Newton’s iteration can be carried out more efficiently. In general, for the four classes of structured matrices of Definition 1, we usually associate various linear displacement operators ![]() of Sylvester type
of Sylvester type ![]() and/or Stein type
and/or Stein type![]() . In this case, Newton’s iteration can be efficiently applied and rapidly improves a rough initial approximation to the inverse, but also destroys the structure of the four classes of structured matrices. Therefore, Newton’s iteration has to be modified to preserve the initial displacement struc- ture of the input structure matrix during the iteration and maintain matrix structure throughout the computation. The main idea here is to control the growth of the length of the short displacement generators so that we can operate with matrices of low rank and carry out the computations much faster. This can be done based on one of the following two techniques. The first technique is to periodically chop off the components corresponding to the smallest singular values in the SVDs of the displacement matrices defined by their generators. This tech- nique can be applied to a Toeplitz-like input matrix. For a Cauchy-like input matrix
. In this case, Newton’s iteration can be efficiently applied and rapidly improves a rough initial approximation to the inverse, but also destroys the structure of the four classes of structured matrices. Therefore, Newton’s iteration has to be modified to preserve the initial displacement struc- ture of the input structure matrix during the iteration and maintain matrix structure throughout the computation. The main idea here is to control the growth of the length of the short displacement generators so that we can operate with matrices of low rank and carry out the computations much faster. This can be done based on one of the following two techniques. The first technique is to periodically chop off the components corresponding to the smallest singular values in the SVDs of the displacement matrices defined by their generators. This tech- nique can be applied to a Toeplitz-like input matrix. For a Cauchy-like input matrix![]() , there is no need to involve the SVD due to the availability of the inverse formula for
, there is no need to involve the SVD due to the availability of the inverse formula for ![]() [10] . The second technique is to control the growth of the length of the generators. This can be done by substituting the approximate inverses for the inverse matrix into its displacement. Here we assume that the matrices involved can be expressed via their displacement generators. Now, let us assume that the matrices
[10] . The second technique is to control the growth of the length of the generators. This can be done by substituting the approximate inverses for the inverse matrix into its displacement. Here we assume that the matrices involved can be expressed via their displacement generators. Now, let us assume that the matrices ![]() and
and ![]() have short generators
have short generators ![]() and
and ![]() respectively. So by operating with short
respectively. So by operating with short ![]() -generators of the matrices
-generators of the matrices![]() ,
, ![]() , and
, and ![]() (or
(or![]() ), we will have to modify Newton’s iteration and use one of the above two techniques to control the length of a
), we will have to modify Newton’s iteration and use one of the above two techniques to control the length of a ![]() -generator of
-generator of![]() , which seems to triple at every iterative step of (6). The same technique applies in the case when
, which seems to triple at every iterative step of (6). The same technique applies in the case when ![]() and
and ![]() -generators are used. In this paper, we restrict our presentation to
-generators are used. In this paper, we restrict our presentation to ![]() -generators (see Theorem 1).
-generators (see Theorem 1).
5.2. SVD-Based Compression of the Generators
For a fixed operator ![]() and a matrix
and a matrix![]() , one can choose the orthogonal (SVD-based)
, one can choose the orthogonal (SVD-based) ![]() -generator matrices to obtain better numerical stability [11] .
-generator matrices to obtain better numerical stability [11] .
Definition 7 A matrix ![]() is said to be unitary iff
is said to be unitary iff![]() . For real matrices,
. For real matrices, ![]() is orthogonal iff
is orthogonal iff![]() . If
. If ![]() is orthogonal, then
is orthogonal, then ![]() form an orthogonal basis for
form an orthogonal basis for![]() .
.
Definition 8 Every ![]() matrix
matrix ![]() has its SVD (singular value decomposition):
has its SVD (singular value decomposition):
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
where![]() ,
, ![]() are singular values of the matrix W,
are singular values of the matrix W, ![]() and
and ![]() denote the Hermitian (conjugate) transpose of the orthogonal matrices
denote the Hermitian (conjugate) transpose of the orthogonal matrices ![]() and
and![]() , respectively. That is,
, respectively. That is, ![]() and
and![]() .
.
Note that if ![]() and
and ![]() are real matrices, then
are real matrices, then ![]() and
and![]() . Based on the SVD of a matrix W, its orthogonal generator of the minimum length is defined by
. Based on the SVD of a matrix W, its orthogonal generator of the minimum length is defined by
![]() (11)
(11)
However, one can use an alternative diagonal scaling, in this case (11) can be written as
![]() . (12)
. (12)
Note that if ![]() for a matrix
for a matrix![]() , then the pair
, then the pair ![]() is an orthogonal L-generator of minimum length for the matrix
is an orthogonal L-generator of minimum length for the matrix![]() .
.
Example 4 Consider the following matrix![]() .
.
Using Matlab command “![]() ” produces the above results. Clearly,
” produces the above results. Clearly, ![]() is the largest singular value and
is the largest singular value and ![]() is the smallest singular value.
is the smallest singular value.![]() ,
, ![]() , and
, and
![]() (Frobenius norm). Furthermore, by (12),
(Frobenius norm). Furthermore, by (12), ![]() and
and
![]() . Note that
. Note that![]() .
.
Remark 3 In numerical computation of the SVD with a fixed positive tolerance ![]() to the output errors caused by rounding (
to the output errors caused by rounding (![]() is the output error bound which is also an upper bound on all the output errors of the singular values
is the output error bound which is also an upper bound on all the output errors of the singular values ![]() and the entries of the computed matrices
and the entries of the computed matrices ![]() and
and ![]() and for
and for![]() ), one truncates (sets to zero) all the smallest singular values
), one truncates (sets to zero) all the smallest singular values ![]() up to
up to![]() . This will produce a numerical orthogonal generator
. This will produce a numerical orthogonal generator ![]() of
of ![]() -length
-length ![]() for a matrix
for a matrix![]() , which is also a numerical orthogonal L-generator for
, which is also a numerical orthogonal L-generator for![]() . Here,
. Here, ![]() is the
is the ![]() -rank of the matrix
-rank of the matrix![]() , which is equal to the minimum number of the singular values of the displacement
, which is equal to the minimum number of the singular values of the displacement ![]() exceeding
exceeding![]() ,
,![]() .
.
Theorem 5 ([9] , p. 79) Given a matrix ![]() of rank
of rank ![]() and a nonnegative integer
and a nonnegative integer ![]() such that
such that![]() , it
, it
holds that![]() . That is, the error in the optimal choice of an approximate of
. That is, the error in the optimal choice of an approximate of ![]() whose
whose
rank does not exceed ![]() is equal to the
is equal to the ![]() -th singular value of
-th singular value of![]() .
.
Theorem 6 If M is a nonsingular matrix, then![]() .
.
Proof.![]() . On the other hand,
. On the other hand,
![]() . This
. This
implies that![]() .
. ![]()
Definition 9 Let![]() ,
, ![]() ,
,![]() . We define
. We define
![]() (13)
(13)
![]() . (14)
. (14)
6. Our Main Algorithm and Results
Outline of the Techniques
By Theorem 6, we assume that ![]() and
and![]() . The ma-
. The ma-
trices ![]() that approximate
that approximate ![]() for large
for large ![]() have a nearby matrix of
have a nearby matrix of ![]() -displacement rank
-displacement rank ![]() for large
for large![]() . This fact motivates the following approach to decrease the computational cost of the iteration in (6): We will replace
. This fact motivates the following approach to decrease the computational cost of the iteration in (6): We will replace ![]() in (6) with a nearby matrix
in (6) with a nearby matrix ![]() having
having ![]() -displacement rank of at most
-displacement rank of at most ![]() and then restart the iteration with
and then restart the iteration with ![]() instead of
instead of![]() . The advantage of this modification is the decrease of the computational cost at the
. The advantage of this modification is the decrease of the computational cost at the ![]() -th Newton step and at all subsequent steps. However, the disadvantage is a possible deterioration of the approximation, since we do not know
-th Newton step and at all subsequent steps. However, the disadvantage is a possible deterioration of the approximation, since we do not know![]() , and the transition from
, and the transition from ![]() to
to ![]() may occur in a wrong direction. But since
may occur in a wrong direction. But since ![]() and
and ![]() are supposed to lie close to
are supposed to lie close to![]() , hence they both lie close to each other. This observation enables us to bound the deterioration of the approximation relative to the current approximation error, so that the quadratic improvement in the error bound at the next step of Newton’s iteration will imme- diately compensate us for such a deterioration. Furthermore, the transition from
, hence they both lie close to each other. This observation enables us to bound the deterioration of the approximation relative to the current approximation error, so that the quadratic improvement in the error bound at the next step of Newton’s iteration will imme- diately compensate us for such a deterioration. Furthermore, the transition from ![]() to a nearby matrix
to a nearby matrix ![]() of a small displacement rank can be done at a low computational cost. In the next main algorithm we describe this approach for Sylvester type operators only. The same results can be extended to Stein operators
of a small displacement rank can be done at a low computational cost. In the next main algorithm we describe this approach for Sylvester type operators only. The same results can be extended to Stein operators ![]() using Theorem 1 with slight modifications to the technique and the theory.
using Theorem 1 with slight modifications to the technique and the theory.
Algorithm 1 (Newton’s Iteration Using Sylverster Type Operators)
INPUT: An integer![]() , two matrices
, two matrices ![]() and
and ![]() defining the operator
defining the operator![]() , an
, an ![]() nonsingular structured matrix
nonsingular structured matrix ![]() having
having ![]() -rank
-rank ![]() and defined by its
and defined by its ![]() -generator
-generator ![]() of length at most
of length at most![]() , a sufficiently close initial approximation
, a sufficiently close initial approximation ![]() to the inverse
to the inverse ![]() given with its
given with its ![]() -generator of length at most
-generator of length at most![]() , an upper bound
, an upper bound ![]() on the number of Newton’s iteration steps, and a compression subalgorithm
on the number of Newton’s iteration steps, and a compression subalgorithm ![]() or
or ![]() for the transition from a
for the transition from a ![]() -generator of length at most
-generator of length at most ![]() for an
for an ![]() matrix approximating
matrix approximating ![]() to
to ![]() -generator of length at most
-generator of length at most ![]() for a nearby matrix.
for a nearby matrix.
OUTPUT: A ![]() -generator of length at most
-generator of length at most ![]() for a matrix
for a matrix ![]() approximating
approximating![]() .
.
COMPUTATION: For![]() , recursively compute a
, recursively compute a ![]() -generators of length at most
-generators of length at most ![]() for the matrices
for the matrices
![]() (15)
(15)
and then apply the compression subalgorithm ![]() or
or ![]() (transition from
(transition from ![]() to
to![]() ) to the matrix
) to the matrix ![]() to compute
to compute ![]() -generators of length at most
-generators of length at most ![]() for the matrices
for the matrices![]() .
.
At the ![]() -th step of (15) of Algorithm 1, a
-th step of (15) of Algorithm 1, a ![]() -generator of length at most
-generator of length at most ![]() for the matrix
for the matrix ![]() can be computed using
can be computed using ![]() flops, for
flops, for![]() . As mentioned earlier, the main idea is to control the growth of the length of the short displacement generators. So the question is how can we control the length of the computed
. As mentioned earlier, the main idea is to control the growth of the length of the short displacement generators. So the question is how can we control the length of the computed ![]() -generators? That is, we need to compress the length of the generators. Therefore, to complete Algorithm 1, we need to introduce two compression subalgorithms, namely, subalgorithm
-generators? That is, we need to compress the length of the generators. Therefore, to complete Algorithm 1, we need to introduce two compression subalgorithms, namely, subalgorithm ![]() and
and![]() . First,
. First,
we describe the compression subalgorithm ![]() based on the SVD of the displacement
based on the SVD of the displacement![]() . To do this,
. To do this,
we compute the SVD based orthogonal generator of the displacement ![]() and decrease the length of the
and decrease the length of the ![]() -generator to
-generator to ![]() by zeroing (truncating) all singular values
by zeroing (truncating) all singular values ![]() for
for![]() . Then output the resulting orthogonal
. Then output the resulting orthogonal ![]() -generator of at most
-generator of at most ![]() for a nearby matrix
for a nearby matrix ![]() which is unique and lies near
which is unique and lies near![]() .
.
Remark 4 By Theorem 5 we can deduce that ![]() because
because
![]() and this also implies that
and this also implies that ![]() lies near
lies near ![]() if the operator
if the operator ![]() is invertible.
is invertible.
Lemma 2 (1)![]() , (2)
, (2)![]() , where
, where ![]() as in (13).
as in (13).
Proof. 1) Since ![]() (largest singular value), then (1) follows from this fact. 2) Since
(largest singular value), then (1) follows from this fact. 2) Since
![]() then
then![]() . Now,
. Now,
![]()
![]()
![]()
Lemma 3![]() , where
, where ![]() as in (13).
as in (13).
Proof. Using the estimate from ([9] , p. 442), that is, for any two matrices ![]() and
and![]() ,
,
![]() for
for ![]() and conclude that
and conclude that
![]() where
where ![]() are defined in (8) - (10) of
are defined in (8) - (10) of
Definition 8. For all ![]() we have
we have ![]() and then we obtain
and then we obtain
![]() . Now, we use (2) of Lemma 2 and deduce
. Now, we use (2) of Lemma 2 and deduce
![]() , for
, for![]() . If we combine the latest inequality with equation (1) of Lemma 2
. If we combine the latest inequality with equation (1) of Lemma 2
for![]() , then we conclude that
, then we conclude that![]() .
. ![]()
Now let us use Lemma 2 and Lemma 3 to prove the bound in the next theorem.
Theorem 7 If ![]() is a nonsingular linear operator and
is a nonsingular linear operator and ![]() is a positive scalar defined in (13), then the
is a positive scalar defined in (13), then the
bound ![]() holds for
holds for ![]() of Definition 6.
of Definition 6.
Proof. By Definition 6 replacing L by![]() , d = 2, and M by Xi − Yi we have
, d = 2, and M by Xi − Yi we have![]() ,
,
which implies that ![]() by linearity of
by linearity of![]() . Now,
. Now,
![]() . Then replace
. Then replace ![]() and
and
![]() to deduce
to deduce
![]() . Finally, use the inequality of Lemma 3 to
. Finally, use the inequality of Lemma 3 to
conclude that![]() . This completes the proof.
. This completes the proof. ![]()
Subalgorithm 1 (![]() : Compression of Displacement by Truncation of their Smallest Singular Values.)
: Compression of Displacement by Truncation of their Smallest Singular Values.)
INPUT: An integer![]() , two matrices
, two matrices ![]() and
and ![]() defining the operator
defining the operator ![]() for an
for an ![]() nonsingular
nonsingular
structured matrices![]() ,
, ![]() , and a
, and a ![]() -generator
-generator ![]() of length
of length
at most ![]() for a matrix
for a matrix ![]() such that
such that![]() ,
,![]() .
.
OUTPUT: A ![]() -displacement generator of length at most
-displacement generator of length at most ![]() for a matrix
for a matrix ![]() such that
such that
![]() , where
, where ![]() as in (13) and
as in (13) and ![]() of Definition 6.
of Definition 6.
COMPUTATIONS: Compute the SVD of the displacement ![]() (the computation is not costly since it is performed with
(the computation is not costly since it is performed with![]() , where
, where![]() ,
, ![]() and since
and since ![]() is small, see [11] ). Set to zero the diagonal entries
is small, see [11] ). Set to zero the diagonal entries ![]() of
of![]() , that is, turning
, that is, turning ![]() into a diagonal matrix of rank at most
into a diagonal matrix of rank at most![]() . (
. (![]() are
are ![]() smallest singular values of the matrix
smallest singular values of the matrix![]() .) Compute and output the matrices
.) Compute and output the matrices![]() ,
, ![]() obtained from
obtained from ![]() and
and ![]() respectively, by deleting their last
respectively, by deleting their last ![]() columns.
columns.
Example 5 For![]() , consider the operator
, consider the operator![]() ,
, ![]() where the
where the
pair![]() ,
, ![]() is the orthogonal, SVD based generator for the displacement
is the orthogonal, SVD based generator for the displacement![]() . Let
. Let
![]() . Then Subalgorithm 1 is applied to the matrix
. Then Subalgorithm 1 is applied to the matrix ![]() and outputs the
and outputs the
matrix![]() . The computational cost of performing Subalgorithm 1 is dominated
. The computational cost of performing Subalgorithm 1 is dominated
by the computation of the SVD of the displacement which requires ![]() flops for
flops for![]() .
.
Next, we will present the second compression technique based on substitution which does not depend on the SVD. By Theorem 4 we conclude that![]() , and by Theorem 3 we
, and by Theorem 3 we
also have ![]() if
if ![]() is nonsingular, and
is nonsingular, and
![]() if
if ![]() is nonsingular. Clearly this expresses the displacement of
is nonsingular. Clearly this expresses the displacement of ![]() via the displacement of
via the displacement of![]() , the operator matrices
, the operator matrices ![]() and
and![]() , and the product of the inverse with
, and the product of the inverse with ![]() specified vectors, where
specified vectors, where ![]() for
for ![]() or
or![]() . Now since
. Now since
![]() , let us substitute
, let us substitute ![]() for
for ![]() on the right hand side and define a short
on the right hand side and define a short ![]() -
-
generator for the matrix![]() :
:
![]() (16)
(16)
Since![]() , we expect
, we expect ![]() because
because![]() .
.
Subalgorithm 2 (![]() : Compression of the displacement by substitution.)
: Compression of the displacement by substitution.)
INPUT: An integer![]() , a pair of
, a pair of ![]() operator matrices
operator matrices ![]() and
and ![]() defining the operator
defining the operator![]() , a
, a ![]() -generator of length r for a nonsingular
-generator of length r for a nonsingular ![]() matrix M where
matrix M where![]() ,
,
and a ![]() -generator
-generator ![]() of length at most
of length at most ![]() for a matrix
for a matrix ![]() of Newton’s iteration (6).
of Newton’s iteration (6).
OUTPUT: A ![]() -generator
-generator ![]() of length at most
of length at most ![]() for a matrix
for a matrix ![]() satisfying the equation
satisfying the equation
![]() with the bound
with the bound
![]() (17)
(17)
where![]() ,
, ![]() of Definition 6,
of Definition 6, ![]() of (14), and for
of (14), and for ![]() of (13).
of (13).
COMPUTATIONS: Compute the matrix products
![]() (18)
(18)
and
![]() . (19)
. (19)
Now the pair ![]() is a
is a ![]() -generator of length at most
-generator of length at most ![]() for a matrix
for a matrix ![]() satisfying the equation
satisfying the equation
![]() . Here we assume the operator
. Here we assume the operator![]() , then the matrix
, then the matrix ![]() is uniquely defined by its L-
is uniquely defined by its L-
generators![]() ,
, ![]() and thus (18) and (19) completely define Newton’s process without involving the matrix
and thus (18) and (19) completely define Newton’s process without involving the matrix
![]() in
in![]() . This subalgorithm achieves compression because
. This subalgorithm achieves compression because![]() ,
,
and preserves approximation. Since![]() , we deduce from Theorem 3 that
, we deduce from Theorem 3 that
![]() . The computation of the
. The computation of the ![]() matrices of (16) is reduced to multi-
matrices of (16) is reduced to multi-
plication of the matrix ![]() by the
by the ![]() matrix
matrix ![]() which requires
which requires ![]() flops for
flops for![]() .
.
Now, we need to prove bound (17).
Theorem 8 For the matrices![]() ,
, ![]() ,
, ![]() , and for
, and for![]() , we
, we
have![]() .
.
Proof. Recall the matrix equations![]() , and
, and![]() . Then we can write
. Then we can write
![]() , and
, and
![]() . Now, let us write
. Now, let us write![]() , then
, then
![]()
Now, take the norm of![]() :
:
![]()
Simplifying the latest inequality yield the following bound:
![]() (20)
(20)
![]()
Theorem 9 For ![]() and
and ![]() for
for ![]() in (13) and
in (13) and ![]() of
of
Definition 6. Then we have ![]() for
for![]() .
.
Proof. Recall that![]() , and since the operator
, and since the operator ![]() is linear, then we
is linear, then we
have![]() . If we use (20) for
. If we use (20) for![]() , we get
, we get
![]() . Therefore,
. Therefore,![]() .
. ![]()
7. Numerical Experiments
Algorithm 1 was tested numerically for ![]() Toeplitz input matrices
Toeplitz input matrices ![]() by applying the compression Su- balgoritm 1. We use Matlab 8.3.0 on a Window 7 machine to run our tests. The Matlab SVD subroutine was used to obtain the singular value decomposition. In general, the complexity of the SVD on an
by applying the compression Su- balgoritm 1. We use Matlab 8.3.0 on a Window 7 machine to run our tests. The Matlab SVD subroutine was used to obtain the singular value decomposition. In general, the complexity of the SVD on an ![]() square matrix is
square matrix is ![]() arithmetic operations. However, it is actually applied to structured matrices with smaller rank, so it is not really expensive. In addition, CLAPACK is one of the faster SVD algorithms that can be applied on real and complex matrices with less time complexity (see [11] ). The tests results are summarized in the follow- ing example.
arithmetic operations. However, it is actually applied to structured matrices with smaller rank, so it is not really expensive. In addition, CLAPACK is one of the faster SVD algorithms that can be applied on real and complex matrices with less time complexity (see [11] ). The tests results are summarized in the follow- ing example.
Example 6 ![]() refers to number of Newton’s steps,
refers to number of Newton’s steps, ![]() is the matrix size,
is the matrix size, ![]() is number of times we ran the test,
is number of times we ran the test, ![]() is a selected bound, and
is a selected bound, and ![]() is the condition number of
is the condition number of![]() , where
, where ![]() is the
is the ![]() -th condition number of the matrix
-th condition number of the matrix![]() . We restricted our numerical experiments to the following classes of
. We restricted our numerical experiments to the following classes of ![]() Toeplitz matrices:
Toeplitz matrices:
1) Real symmetric tridiagonal Toeplitz matrices:![]() ,
, ![]() where
where![]() ,
, ![]() ,
,
![]() (the first table of Table 3) or
(the first table of Table 3) or ![]() (the second table of Table 3) (see Figure 1).
(the second table of Table 3) (see Figure 1).
2) The matrices ![]() (third table represents symmetric positive definite and the fourth table
(third table represents symmetric positive definite and the fourth table
represents symmetric positive indefinite of Table 3) (see Figure 1).
3) Randomly generated Toeplitz matrices, whose entries are chosen randomly from the interval ![]() and are uniformly distributed with mean 0 and standard deviation of 1 (see Table 4 and Figure 2).
and are uniformly distributed with mean 0 and standard deviation of 1 (see Table 4 and Figure 2).
For a symmetric positive definite matrix M, the initial matrix ![]() was used, whereas for unsym-
was used, whereas for unsym-
metric and symmetric indefinite Toeplitz matrices M, Newton’s iteration was initialized with![]() .
.
![]()
![]()
Table 3. First top two tables represent Tridiagonal Matrices of Class 1 and the last two tables represent matrices of Class 2.
![]()
![]()
Table 4. Random Matrices of Class 3.
Acknowledgements
We thank the editor and the referees for their comments.
References
- Kailath, T. and Sayed, A. (1999) Fast Reliable Algorithms for Matrices with Structure. Society for Industrial and Applied Mathematics, Philadelphia. http://dx.doi.org/10.1137/1.9781611971354
- Pan, V.Y., Branham, S., Rosholt, R. and Zheng, A. (1999) Newton’s Iteration for Structured Matrices and Linear Systems of Equations, SIAM Volume on Fast Reliable Algorithms for Matrices with Structure. Society for Industrial and Applied Mathematics, Philadelphia.
- Pan, V.Y., Zheng, A.L., Huang, X.H. and Dias, O. (1997) Newton’s Iteration for Inversion of Cauchy-Like and Other Structured Matrices. Journal of Complexity, 13, 108-124. http://dx.doi.org/10.1006/jcom.1997.0431
- Bini, D. and Pan, V.Y. (1994) Polynomial and Matrix Computations, Vol. 1 Fundamental Algorithms. Birkhäuser, Boston.
- Pan, V.Y. (2001) Structured Matrices and Polynomials: Unified Superfast Algorithms. Birkhäuser, Boston.
- Kailath, T., Kung, S.-Y. and Morf, M. (1979) Displacement Ranks of Matrices and Linear Equations. Journal of Mathematical Analysis and Applications, 68, 395-407. http://dx.doi.org/10.1016/0022-247X(79)90124-0
- Kailath, T. and Sayed, A.H. (2002) Displacement Structure: Theory and Applications. SIAM Review, 37, 297-386. http://dx.doi.org/10.1137/1037082
- Pan, V.Y. and Rami, Y. (2001) Newton’s Iteration for the Inversion of Structured Matrices. In: Bini, D., Tyrtyshnikov, E. and Yalamov, P., Eds., Structured Matrices: Recent Developments in Theory and Computation, Nova Science Publishers, New York, 79-90.
- Golub, G.H. and Van Loan, C.F. (2013) Matrix Computations. 4th Edition, John Hopkins University Press, Baltimore.
- Heinig, G. (1995) Inversion of Generalized Cauchy Matrices and the Other Classes of Structured Matrices. The IMA Volume in Mathematics and Its Applications, 69, 63-81.
- Pan, V.Y. (1993) Decreasing the Displacement Rank of a Matrix. SIAM Journal on Matrix Analysis and Application, 14, 118-121. http://dx.doi.org/10.1137/0614010



 rapidly refines a crude initial approximation
rapidly refines a crude initial approximation 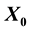 to the inverse of a general nonsingular matrix. In this paper, we will extend and apply this me- thod to
to the inverse of a general nonsingular matrix. In this paper, we will extend and apply this me- thod to 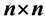 structured matrices
structured matrices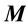 , in which matrix multiplication has a lower computational cost. These matrices can be represented by their short generators which allow faster compu- tations based on the displacement operators tool. However, the length of the generators is tend to grow and the iterations do not preserve matrix structure. So, the main goal is to control the grow- th of the length of the short displacement generators so that we can operate with matrices of low rank and carry out the computations much faster. In order to achieve our goal, we will compress the computed approximations to the inverse to yield a superfast algorithm. We will describe two different compression techniques based on the SVD and substitution and we will analyze these approaches. Our main algorithm can be applied to more general classes of structured matrices.
, in which matrix multiplication has a lower computational cost. These matrices can be represented by their short generators which allow faster compu- tations based on the displacement operators tool. However, the length of the generators is tend to grow and the iterations do not preserve matrix structure. So, the main goal is to control the grow- th of the length of the short displacement generators so that we can operate with matrices of low rank and carry out the computations much faster. In order to achieve our goal, we will compress the computed approximations to the inverse to yield a superfast algorithm. We will describe two different compression techniques based on the SVD and substitution and we will analyze these approaches. Our main algorithm can be applied to more general classes of structured matrices.
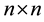 dense structured matrices dramatically decreases in comparison with the general
dense structured matrices dramatically decreases in comparison with the general 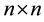 matrices, that is, from the order of
matrices, that is, from the order of  words of storage space and
words of storage space and  arithmetic operations (ops) with
arithmetic operations (ops) with 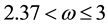 in the best algorithms, to
in the best algorithms, to  words of storage space and to
words of storage space and to  ops (and sometimes to
ops (and sometimes to  ops) (Table 1). The displacement rank
ops) (Table 1). The displacement rank 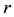 for an
for an 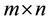 Toeplitz and Hankel matrix is at most 2. A matrix is Toeplitz-like or Hankel-like if
Toeplitz and Hankel matrix is at most 2. A matrix is Toeplitz-like or Hankel-like if  is small or bounded by a small constant independent of
is small or bounded by a small constant independent of 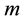 and
and






































































































































































































































































































































































































































































































































































































































































































