Advances in Linear Algebra & Matrix Theory
Vol.4 No.1(2014), Article ID:43469,8 pages DOI:10.4236/alamt.2014.41001
Parallel Multicore CSB Format and Its Sparse Matrix Vector Multiplication*
Bing Yang1, Shuo Gu2, Tong-Xiang Gu3#, Cong Zheng1, Xing-Ping Liu3
1Graduate School of Chinese Academy of Engineering Physics, Beijing, China
2School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu, China
3Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing, China
Email: #txgu@iapcm.ac.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 6 January 2014; revised 7 February 2014; accepted 14 February 2014
ABSTRACT
Sparse Matrix Vector Multiplication (SpMV) is one of the most basic problems in scientific and engineering computations. It is the basic operation in many realms, such as solving linear systems or eigenvalue problems. Nowadays, more than 90 percent of the world’s highest performance parallel computers in the top 500 use multicore architecture. So it is important practically to design the efficient methods of computing SpMV on multicore parallel computers. Usually, algorithms based on compressed sparse row (CSR) format suffer from a number of nonzero elements on each row so hardly as to use the multicore structure efficiently. Compressed Sparse Block (CSB) format is an effective storage format which can compute SpMV efficiently in a multicore computer. This paper presents a parallel multicore CSB format and SpMV based on it. We carried out numerical experiments on a parallel multicore computer. The results show that our parallel multicore CSB format and SpMV algorithm can reach high speedup, and they are highly scalable for banded matrices.
Keywords:SpMV; Multicore Parallel Computers; Parallel Multicore CSB Format

1. Introduction
With the development of science and technology, people need to deal with the increasing scale of the problems, which leads to the increasing computational overhead. As an essential operation in computational science, sparse matrix-vector multiplication (SpMV) is the most costly step in solving linear systems and eigenvalue problems. So improving the performance of the SpMV is often able to enhance the overall performance.
In order to solve practical problems efficiently, we not only need to design efficient algorithms, but also need to improve calculation tools. So there are more and more applications of massively parallel computers in engineering calculations. Statistics released twice a year to become the world’s TOP 500 becomes the valid measure of the top computing power. Nowadays, all of TOP 500 supercomputers have been cluster structures, more than 90 percent of which have a multicore structure with at least 4 cores in 1 CPU [1] . This means that how to improve the SpMV kernel in multicore parallel computers is crucial to raise the parallel performance and parallel efficiency.
There are some methods to improve the efficiency of SpMV. Autotuning used in pOSKI [2] and other solvers can optimize for different supercomputers and different problems. Cache partition [3] and reordering [4] can reduce the communication bandwidth. And we will focus on the matrix storage format and the SpMV algorithm. CSB format, which is proposed in 2009, can store a sparse matrix with a similar storage usage as CSR format [5] . This format, designed for the multicore computer, can maintain load balance dynamically. We extend CSB format to the parallel multicore computer in this paper.
The remainder of the paper is organized as follows: Section 2 introduces the basic CSB format and its SpMV method. Section 3 describes multicore CSB format and some methods we use to enhance the parallel performance. Section 4 introduces our experiments and results. Section 5 states the conclusion.
2. Introduction to CSB Format
We provides an overview of the CSB sparse-matrix storage format and describe the multicore SpMV algorithm and its extension to parallel computer in this section.
Firstly, CSB format partitions a 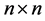 matrix
matrix  into
into 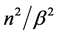 blocks which are of size
blocks which are of size 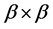 each. Let
each. Let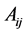 denote the
denote the 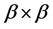 submatrix that has the nonzero elements in the rows
submatrix that has the nonzero elements in the rows 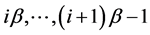 and columns
and columns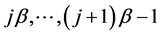 . Within each block
. Within each block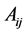 , the Z-morton layout [6] is used to perform the matrix recursively. In practice, the matrix is stored in three arrays. The blk_ptr array tells the first element of each block, the low_ind array holds the lower bit of the row and column index in the block, and the val array stores the numerical values. Noticed that the low_ind array and the val array is of size nonzero numbers (nnz), and if matrix
, the Z-morton layout [6] is used to perform the matrix recursively. In practice, the matrix is stored in three arrays. The blk_ptr array tells the first element of each block, the low_ind array holds the lower bit of the row and column index in the block, and the val array stores the numerical values. Noticed that the low_ind array and the val array is of size nonzero numbers (nnz), and if matrix 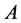 if full, then the blk_ptr array is of size
if full, then the blk_ptr array is of size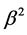 .
.
So there exist three levels of parallelism in the parallel SpMV algorithm. The first level is to compute the blockrow 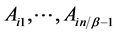 in parallel. If the nonzeros distribute in each blockrow is unevenly, then there exists the second parallel level named “chunk”, which includes of several blocks to balance the load. And if the nonzeros are too many for a single block, then we should deal with the third parallel level in this block, which we partition into four subblocks. And diagonal subblocks and back-diagonal subblocks can be computed without any data races.
in parallel. If the nonzeros distribute in each blockrow is unevenly, then there exists the second parallel level named “chunk”, which includes of several blocks to balance the load. And if the nonzeros are too many for a single block, then we should deal with the third parallel level in this block, which we partition into four subblocks. And diagonal subblocks and back-diagonal subblocks can be computed without any data races.
It can be noticed that OpenMP programming technique is generally used for the data structure 2 to be determined in the compilation. The SpMV of CSB format is based on the recursive calculations at runtime. Therefore, the programming techniques used in this paper is Cilk++ [7] , which can spawn multiple threads by a singlethreaded branch.
3. Parallel Multicore CSB Algorithm
This section introduces multicore CSB storage format, sparse matrix-vector multiplication algorithm and some optimizations for special structures.
3.1. Parallel Multicore CSB Algorithm
Usually, sparse matrix vector multiplication is just a part of a complete algorithm, such as solving linear equations of a step. Therefore, there is no need to reduce the result to the same processor in each step and distributed storage of the result vectors on each processor can meet most of the computational requirements. Meanwhile, the practical application will generate a whole sparse matrix processor and then distribute it to other processors. The normal situation is to generate a local sparse matrix in respective processor. Therefore, the content stored on a processor should be locally sparse matrix, part of the vector, part of the result vector. So the general multicore CSB format and its SpMV algorithm are as followed:
a) Generate a local sparse matrix in common storage format as CSR format b) Convert the common storage format to the CSB format c) Send the appropriate part of the vector to the right processor d) Compute the result using SpMV in CSB format Sometimes, we need to partition a whole sparse matrix and send it to other processors. Assuming that the matrix is stored in columns, the following algorithm can be used:
a) Partition the matrix by columns with load balance, send the sub-matrix to the appropriate processor b) On the respective processor, sub-matrix need be converted into a matrix in CSB format c) Get the right part of the vector which will be multiplied d) Use SpMV in CSB format to compute the result Notice that the result of the second algorithm is still stored in each processor in distribution.
3.2. Banded Matrices Stored in Column
For the banded matrix, we can optimize the algorithm more efficiently.
• Compress the Row Index As shown in Figure 1, what we need deal with is the area bounded by solid lines in the middle of the figure. But if send the column-order submatrix to some CPU without decrease the index of the first nonzero row to 0, it is equal to deal with a taller and thinner matrix, which is costly for more partitions could happen so that more threads will be generated in some CPU. So we can simply decrease the index of the first nonzero row to 0, and change the other nonzero rows at the same way.
• Reduce the Communication Unnecessary As mentioned above, we can find that the global communication to get the result can be transferred to the local communication when we distribute the result vector. Also, we can decrease the communication a bit further. Shown in Figure 2, we can just send what the neighbor processor needs as rounded by the thick dash lines. So we can save some calculations and spaces that are unnecessary originally.
3.3. Non-blocking Communication
Considering that there will be some imbalance in the computation procedure in practice so that some processors compute faster than others. So, when computing the result vector, we use the non-blocking communication so as to improve the communication efficiency.
4. Experiment Design and Results
We design three kinds of experiments to detect the parallel degree and scalability of our algorithm and one experiment to explain the difference between the local communication and the global communication. The first

Figure 1. Example for compressing the row index.
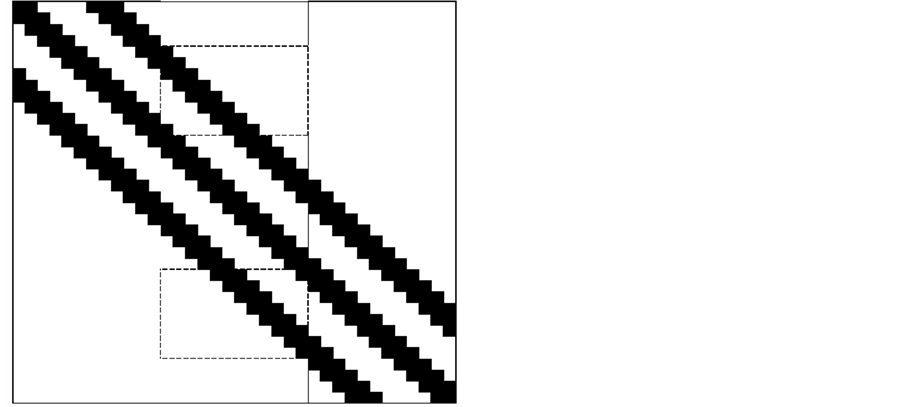
Figure 2. Example for reduce communication unnecessary.
kind of experiments gives the results about applying the plain algorithm to some random matrices, which can explain how the algorithm works. Among these experiments, we used the global or the local communication according to the matrix. The next section will tell how the difference between the local and global communication is by testing a large sparse matrix. Then, we tested the scalability by generate a series of extendible 9-diagonal matrices, which can only use the local communication, in the next kind of experiments.
The platform is Deepcomp 7000 Series, whose blade node has two quad-core Xeon processors E5450, clocked at 3.00 GHz, 32 GB RAM, and the compilation environment is Intel C++ Composer with Intel MPI which supports Cilk++ multi-threads programming.
Meanwhile, there are two main targets to measure our algorithm: speedup and CPU-speedup. They are computed by these equations:
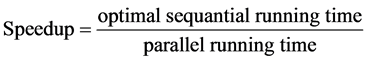 (1)
(1)
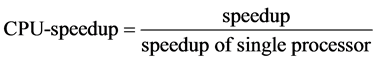 (2)
(2)
As we all know, the running time in a multicore system is very hard to get, so we use the wall time to replace the running time. And optimal sequential algorithm is too hard to get, either. So we run the parallel program in 1 core of 1 processor to get the sequential running wall time. So the actual speedup formula is:
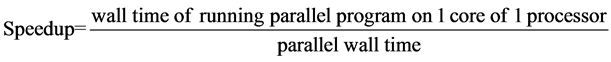 (3)
(3)
Speedup can make it more clear how the algorithm works as a whole while CPU-speedup can tell us how the algorithm works on the multicore architecture supercomputer. For convenience, we fixed to use 4 cores per CPU so as to consider how speedup and CPU speedup change when increasing the number of CPU.
4.1. For random Matrices
We test five square real unsymmetrical matrices downloaded from the Matrix Market [8] and the University of Florida Sparse matrix collection [9] . Table 1 lists some features of these matrices: the size (n), the number of non-zeros (nnz), the average number of non-zeros per row (average), communication style (comm. style).
Actually we use the local communication for the banded matrices but the global communication for the normal matrices. So we illustrated these two situations respectively. As shown in Figure 3, the performance is basically linear with the increasing processor numbers. For example, speedup of matrix atmosmodl increases from 2.5 by one CPU to 18 by twelve CPUs. For the global communication ones, we get the performance peak in the less number, which is shown in Figure 4. According to matrix cage13, speedup increased from 3 by one CPU to 8 by five CPUs, and then decreased to 3 by 12 CPUs.
Mentioned above, we can find that our algorithm can solve all the SpMV multiplication and all the problems could be speeded up more or less. And problems with local communication can get better speedup than those with global communication.
Table 1. The characteristics of random matrices.
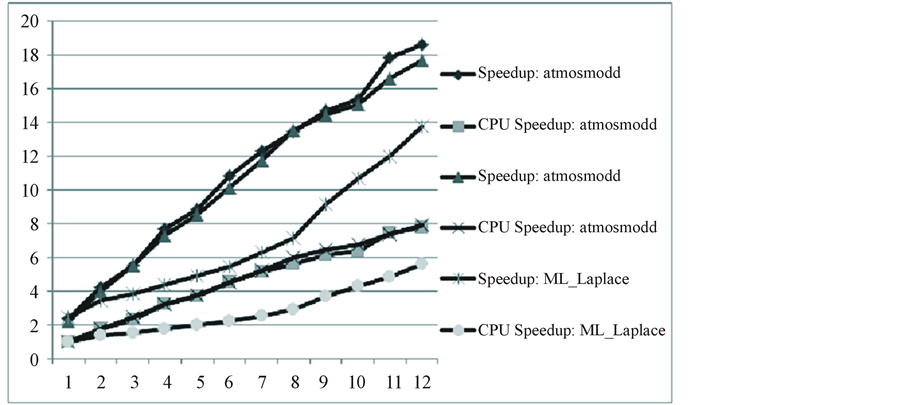
Figure 3. The performance of local communication.
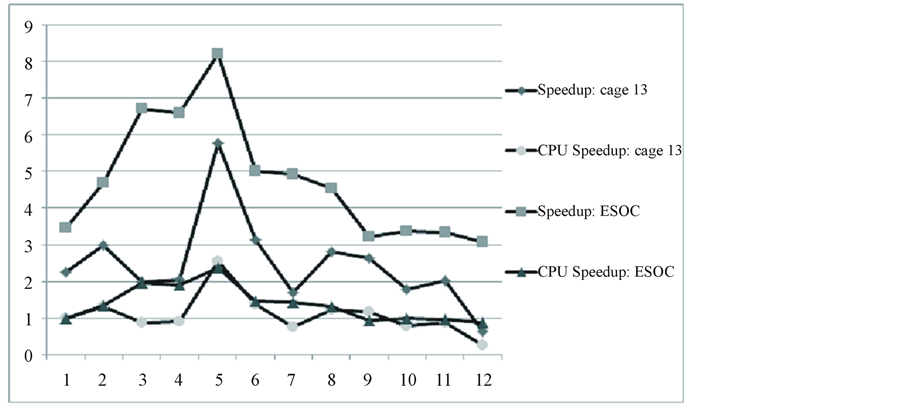
Figure 4. The performance of global communication.
4.2. Communication: Local and Global
In order to illustrate the effect of local communications and global communication to the performance of the algorithm with the increasing number of processors more clearly, we test the nine point format matrix from discretion of a convection-diffusion equation. The convection-diffusion equation is as follows:
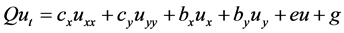 (4)
(4)
where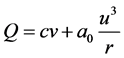 ,
, 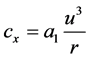 ,
, 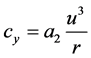 ,
, 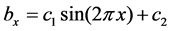 ,
, 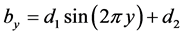 , and
, and
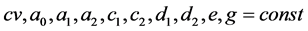 .
.
Testing how the performance changes when the processor number increases for a fixed matrices can reflect some aspect of the algorithm’s scalability. Considering that there may be some great differences when using the local communication or not, we tested the two situations separately. The matrix we dealt with is called yh9p_ 2880, which has 8,294,400 dimensions and 74,615,044 nonzeros with 9-diagonal format. We tested the performance when the processor number is 1, 2, 4, 8, 16, 32, 64 with fixed 4 threads in each processor. And the numerical result is shown in Figure 5.
Notice that there are some superlinear speedup in the graph when the processor number used is 2, 4. The first reason is that we use the MPI even if the processor number used is 1, which causes some extra spending. Meanwhile, analyzing the result, we find that our program choose 16,384 as the maximum element number of one block, which means each block can be of size 256KB (16384 * (8 + 4 + 4) Bytes). When using 2 or 4 processor, it choose 8192 as the maximum element number of one block, which means each block can be of size 128 K (8192 * (8 + 4 + 4) Bytes). We use the parallel computer consisted of xeon X7350, whose L1 cache is 256 KB. So using 1 processor only has more cache miss, which cause the superlinear speedup.
And repeat the same kind experiments but using the global communication, we get the results like Figure 6 as followed:
So we can conclude that if we can simplify the global communication to the local communication, the speedup ratio of the SpMV may increase linearly with the size of problem increases linearly.
4.3. Scalability
We used a group of scalable banded matrices as the tested matrices in Table 2 which can be generated from the equation 4 in last section. We maintain the same number of unknowns among each processor. So we obtain the following properties shown in Figure 7: speedup increase nearly linearly from 2 by a single CPU to 20 by 12 CPUs.
Numerical results show that parallel multicore CSB algorithm is of good scalability.
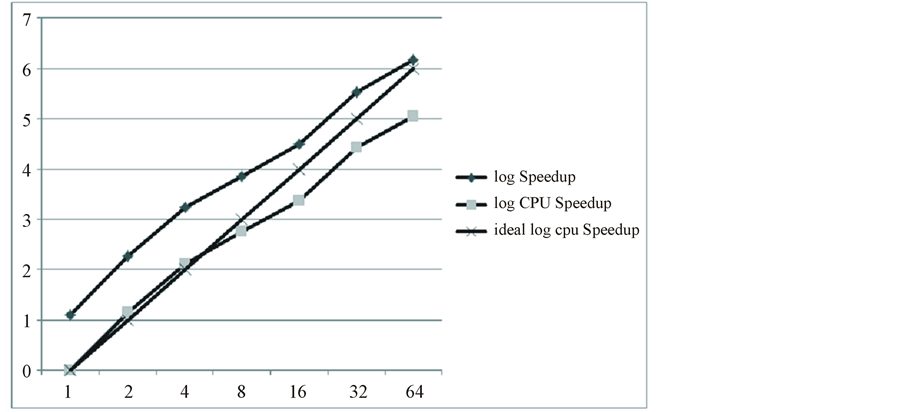
Figure 5. The performance of local communication.
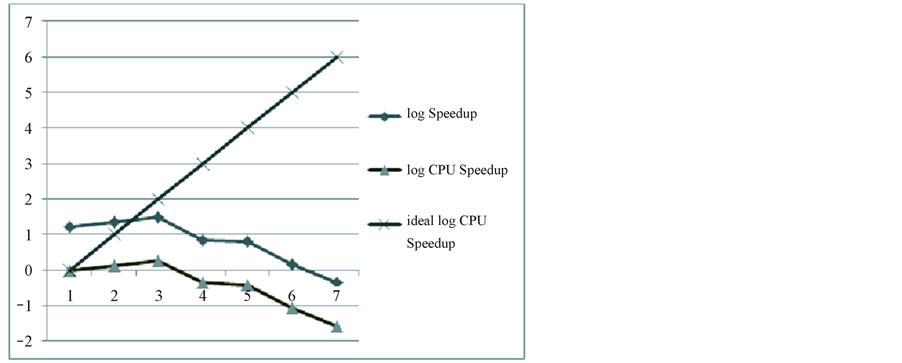
Figure 6. The performance of global communication.
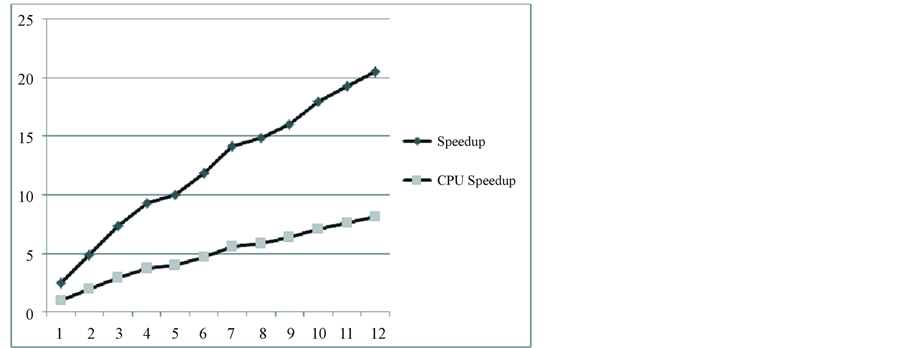
Figure 7. The performance of scalable matrices.
Table 2. The size of scalable matrices.
5. Conclusions
As mentioned above, we can reach such conclusions:
1) Multicore CSB format extends CSB format to suit for the multicore parallel machines.
2) For a specified scaled matrix, local communication can achieve higher performance than global communication.
3) For local communication, the new algorithm has good scalability with the number of processors increasing. But for global communication, performance decreased with the increasing number of processors.
References
- http://www.top500.org/
- Im, E.J., Yelick, K. and Vuduc, R. (2004) Sparsity: Optimization Framework for Sparse Matrix Kernels. International Journal of High Performance Computing Applications, 18, 135-158. http://dx.doi.org/10.1177/1094342004041296
- Morton, G.M. (1966) A Computer Oriented Geodetic Data Base and a New Technique in File Sequencing. IBM Ltd., Ottawa.
- Jain, A. (2008) pOSKI: An Extensible Autotuning Framework to Perform Optimized SpMVs on Multicore Architectures. Master Thesis, Computer Science Department, University of California at Berkeley, Berkeley.
- Saad, Y. (2003) Iterative Methods for Sparse Linear Systems. Society for Industrial Applied Mathematics. http://dx.doi.org/10.1137/1.9780898718003
- Bulu, C.A., Fineman, J.T., Frigo, M., Gilbert, J.R. and Leiserson, E. (2009) Parallel Sparse Matrix-Vector and MatrixTranspose-Vector Multiplication Using Compressed Sparse Blocks. Symposium on Parallelism in Algorithms and Architectures, 233-244.
- Rose, D.J. (1973) A Graph-Theoretic Study of the Numerical Solution of Sparse Positive Definite Systems of Linear Equations. Graph Theory and Computing, 183-217.
- Blumofe, R.D., Joerg, C.F., Kuszmaul, B.C., Leiserson, C.E., Randall, K.H., and Zhou, Y. (1995) Cilk: An Efficient Multithreaded Runtime System. Principles and Practice of Parallel Programming, Santa Barbara, 207-216.
- Boisvert, R., Pozo, R., Remington, K., Miller, B. and Lipman, R. (2000) The Matrix Market. http://math.nist.gov/MatrixMarket/
NOTES

*The project is partly supported by the NSF of China (No. 91130024, No. 61170309) and Major Project of Development Foundation of science and Technology of CAEP (No. 2012A0202008, No. 2011A0202012).
#Corresponding author.


