Advances in Linear Algebra & Matrix Theory
Vol.3 No.2(2013), Article ID:33059,4 pages DOI:10.4236/alamt.2013.32002
Minimal Critical Sets of Refined Inertias for Irreducible Sign Patterns of Order 2
Faculty of Mathematics and Physics, Huaiyin Institute of Technology, Huai’an, China
Email: berlinyu@163.com
Copyright © 2013 Ber-Lin Yu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 1, 2013; revised June 1, 2013; accepted June 8, 2013
Keywords: Associated digraph; Inertially arbitrary sign pattern; Refined inertia; Critical set of refined inertias
ABSTRACT
Let 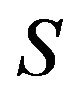 be a nonempty, proper subset of all refined inertias. Then,
be a nonempty, proper subset of all refined inertias. Then, 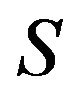 is called a critical set of refined inertias for ireducible sign patterns of order
is called a critical set of refined inertias for ireducible sign patterns of order  if
if 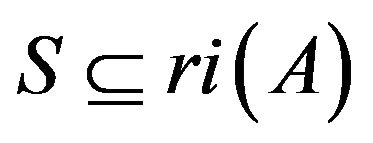 is sufficient for any sign pattern
is sufficient for any sign pattern  to be refined inertially arbitrary. If no proper subset of
to be refined inertially arbitrary. If no proper subset of 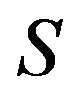 is a critical set of refined inertias, then
is a critical set of refined inertias, then 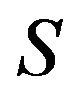 is a minimal critical set of refined inertias for sign patterns of order
is a minimal critical set of refined inertias for sign patterns of order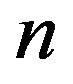 . In this paper, all minimal critical sets of refined inertias for irreducible sign patterns of order 2 are identified. As a by-product, a new approach is presented to identify all minimal critical sets of inertias for irreducible sign patterns of order 2.
. In this paper, all minimal critical sets of refined inertias for irreducible sign patterns of order 2 are identified. As a by-product, a new approach is presented to identify all minimal critical sets of inertias for irreducible sign patterns of order 2.
1. Introduction
A  sign pattern is a matrix
sign pattern is a matrix  with entries from the set
with entries from the set  where
where  (respectively,
(respectively, ) denotes a positive (respectively, negative) real number; see, e.g., [1]. The set of all real matrices with the same sign pattern as the
) denotes a positive (respectively, negative) real number; see, e.g., [1]. The set of all real matrices with the same sign pattern as the 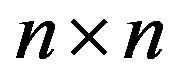 sign pattern
sign pattern  is the qualitative class
is the qualitative class

A subpattern of an 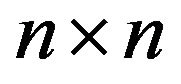 sign pattern
sign pattern  is a sign pattern
is a sign pattern 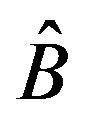 obtained by replacing some (possibly empty) subset of the nonzero entries of
obtained by replacing some (possibly empty) subset of the nonzero entries of  with zeros. If
with zeros. If  is a subpattern of
is a subpattern of , then
, then  is a superpattern of
is a superpattern of . Two square zero-nonzero patterns
. Two square zero-nonzero patterns  and
and  are equivalent if one can be obtained from the other by any combination of transposition and permutation similarity. A sign pattern
are equivalent if one can be obtained from the other by any combination of transposition and permutation similarity. A sign pattern  is reducible if it is permutation similar to a pattern of the form
is reducible if it is permutation similar to a pattern of the form

where 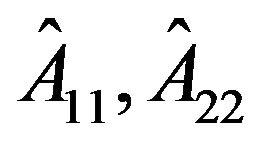 are square and non-vacuous. A pattern is irreducible if it is not reducible.
are square and non-vacuous. A pattern is irreducible if it is not reducible.
The inertia of a matrix  is an ordered triple
is an ordered triple 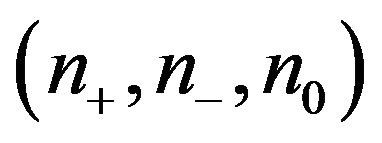 where
where 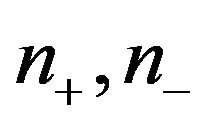 and
and 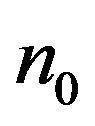 are the number of eigenvalues of
are the number of eigenvalues of  with positive, negative and zero real part, respectively; see, e.g., [2]. The refined inertia of
with positive, negative and zero real part, respectively; see, e.g., [2]. The refined inertia of  is the ordered quadruple
is the ordered quadruple 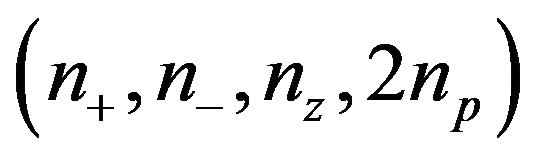 of nonnegative integers that sum to
of nonnegative integers that sum to , where
, where 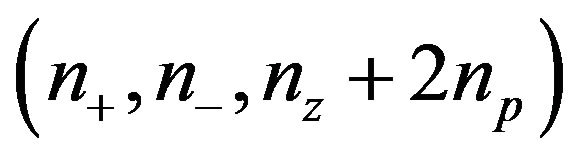 is the inertia of
is the inertia of  while
while 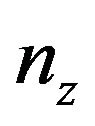 is the number of 0 as an eigenvalue of
is the number of 0 as an eigenvalue of  and
and  is the number of eigenvalues of
is the number of eigenvalues of  with nonzero pure imaginary eigenvalues; see, e.g., [3]. The inertia (respectively, refined inertia) of a sign pattern
with nonzero pure imaginary eigenvalues; see, e.g., [3]. The inertia (respectively, refined inertia) of a sign pattern  is
is 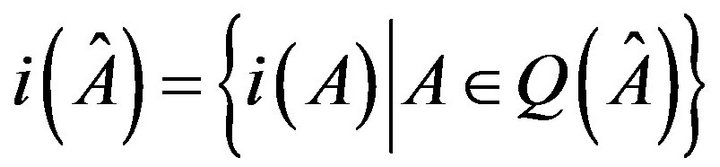 (respectively,
(respectively,
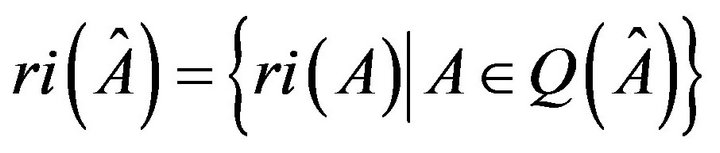 ). A
). A 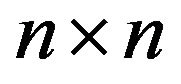 sign pattern
sign pattern 
is an inertially arbitrary pattern (IAP) if given any ordered triple 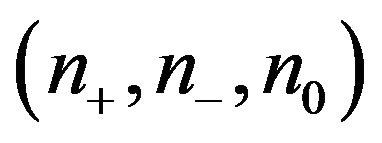 of nonnegative integers with
of nonnegative integers with , there exists a real matrix
, there exists a real matrix 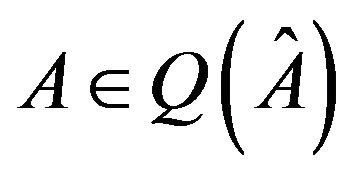
such that ; see, e.g., [4,5] and the reference therein. Similarly,
; see, e.g., [4,5] and the reference therein. Similarly,  is a refined inertially arbitrary pattern (rIAP) if given any ordered quadruple
is a refined inertially arbitrary pattern (rIAP) if given any ordered quadruple  of nonnegative integers that sum to
of nonnegative integers that sum to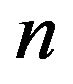 , there exists a real matrix
, there exists a real matrix 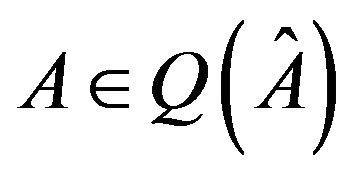 such that
such that 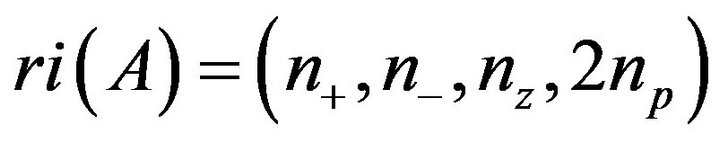 ; see, e.g., [3].
; see, e.g., [3].
Let  be a nonempty, proper subset of the set of all inertias for any
be a nonempty, proper subset of the set of all inertias for any 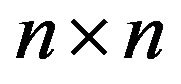 zero-nonzero (or sign) pattern
zero-nonzero (or sign) pattern . If
. If  is sufficient for
is sufficient for  to be inertially arbitrary, then
to be inertially arbitrary, then 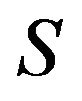 is said to be a critical set of inertias for zero-nonzero (or sign) patterns of order
is said to be a critical set of inertias for zero-nonzero (or sign) patterns of order  and if no proper subset of
and if no proper subset of 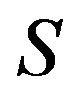 is a critical set of inertias, then
is a critical set of inertias, then 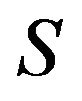 is said to be a minimal critical set of inertias for zerononzero (or sign) patterns of order
is said to be a minimal critical set of inertias for zerononzero (or sign) patterns of order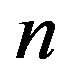 ; see, e.g., [6]. Critical sets of refined inertias for irreducible zero-nonzero patterns are defined in [7]. Similarly, we introduce the concept of a critical set of refined inertias for sign patterns. Let
; see, e.g., [6]. Critical sets of refined inertias for irreducible zero-nonzero patterns are defined in [7]. Similarly, we introduce the concept of a critical set of refined inertias for sign patterns. Let  be a nonempty, proper subset of all refined inertias. Then,
be a nonempty, proper subset of all refined inertias. Then,  is called a critical set of refined inertias for sign patterns of order
is called a critical set of refined inertias for sign patterns of order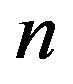 , if the set
, if the set 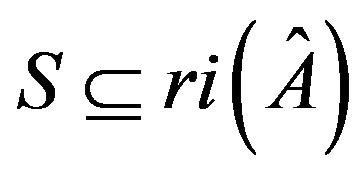 is sufficient for any sign pattern
is sufficient for any sign pattern  to be refined inertially arbitrary. If no proper subset of
to be refined inertially arbitrary. If no proper subset of  is a critical set of refined inertias, then
is a critical set of refined inertias, then 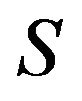 is a minimal critical set of refined inertias for irreducible sign patterns of order
is a minimal critical set of refined inertias for irreducible sign patterns of order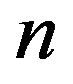 . We note that all minimal critical sets of inertias for irreducible sign patterns of order 2 have been identified in [6]. But, identifying all minimal critical sets of inertias for irreducible zero-nonzero (or sign) patterns of order
. We note that all minimal critical sets of inertias for irreducible sign patterns of order 2 have been identified in [6]. But, identifying all minimal critical sets of inertias for irreducible zero-nonzero (or sign) patterns of order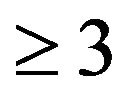 has been posed as an open question in [6]. Also open is the minimum cardinality of such a set. The concept of critical sets of refined inertias for sign pattern is introduced for the first time. In this work, we concentrate on the minimal critical sets of refined inertias for irreducible sign patterns of order 2.
has been posed as an open question in [6]. Also open is the minimum cardinality of such a set. The concept of critical sets of refined inertias for sign pattern is introduced for the first time. In this work, we concentrate on the minimal critical sets of refined inertias for irreducible sign patterns of order 2.
Our work is organized as follows. Section 2 describes some preliminary results on the refined inertias of sign patterns. The minimal critical sets of refined inertias for irreducible sign patterns of order 2 are identified in Section 3. In Section 4, as a by-product, an alternative proof is given to identify all minimal critical sets of inertias for  irreducible sign patterns. Some concluding remarks are given in Section 5.
irreducible sign patterns. Some concluding remarks are given in Section 5.
2. Preliminaries
Recall that a sign pattern  has its associated digraph
has its associated digraph  with vertex set
with vertex set 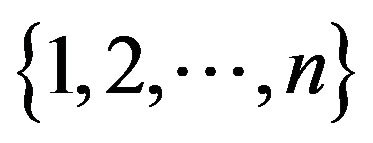 and for all
and for all  and
and , a positive (resp., negative ) arc from
, a positive (resp., negative ) arc from  to
to  if and only if
if and only if 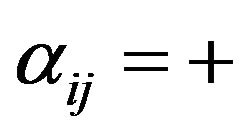 (resp.,
(resp.,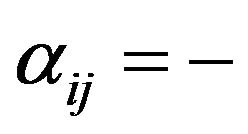 ). A (directed) simple cycle (or a k-cycle)
). A (directed) simple cycle (or a k-cycle)  of length k is a sequence of k arcs
of length k is a sequence of k arcs 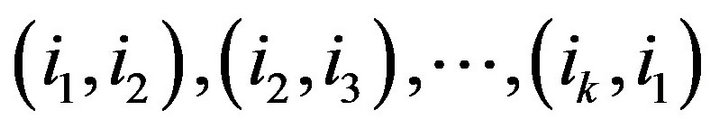 such that these vertices are distinct; see, e.g., [1]. The sign positive (or negative) of a simple cycle in a sign pattern
such that these vertices are distinct; see, e.g., [1]. The sign positive (or negative) of a simple cycle in a sign pattern  is the actual product of the entries in the cycle, following the obvious rules that multiplication is commutative and associative, and (+)(+) = +,(+)(−) = −.
is the actual product of the entries in the cycle, following the obvious rules that multiplication is commutative and associative, and (+)(+) = +,(+)(−) = −.
Lemma 2.1. let  be an irreducible sign pattern of order 2. Then the following are equivalent:
be an irreducible sign pattern of order 2. Then the following are equivalent:
(1)  is spectrally arbitrary;
is spectrally arbitrary;
(2)  is inertially arbitrary;
is inertially arbitrary;
(3) Up to equivalence,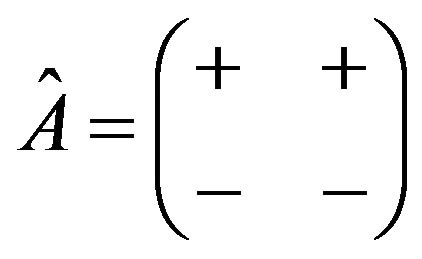 ;
;
(4) Associated digraph of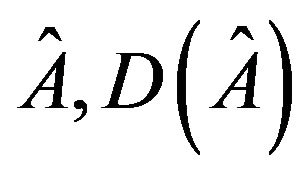 , has two loops of opposite sign and a negative 2-cycle.
, has two loops of opposite sign and a negative 2-cycle.
Proof. The equivalences of  follow from Proposition 3 in [6]. The equivalence of
follow from Proposition 3 in [6]. The equivalence of 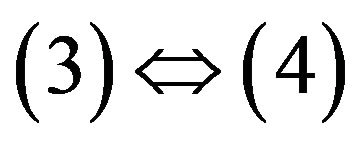 can be verified directly.
can be verified directly.
It is known that there are seven refined inertias for 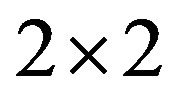 sign patterns. To identify all minimal critical sets of refined inertias for irreducible sign patterns of order 2, the following three sign patterns are necessary to be investigated.
sign patterns. To identify all minimal critical sets of refined inertias for irreducible sign patterns of order 2, the following three sign patterns are necessary to be investigated.
Lemma 2.2. Let 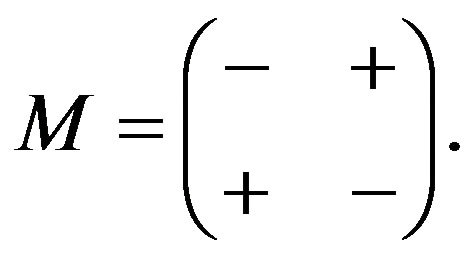 Then,
Then, 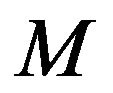 allows the only refined inertias (0, 1, 1, 0), (0, 2, 0, 0) and (1, 1, 0, 0).
allows the only refined inertias (0, 1, 1, 0), (0, 2, 0, 0) and (1, 1, 0, 0).
Proof. Since 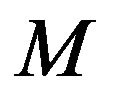 requires every realization with a negative trace, the refined inertias (2, 0, 0, 0), (0, 0, 2, 0), (0, 0, 0, 2) and (1, 0, 1, 0) cannot be allowed by
requires every realization with a negative trace, the refined inertias (2, 0, 0, 0), (0, 0, 2, 0), (0, 0, 0, 2) and (1, 0, 1, 0) cannot be allowed by . For the remaining refined inertias, consider realizations of
. For the remaining refined inertias, consider realizations of
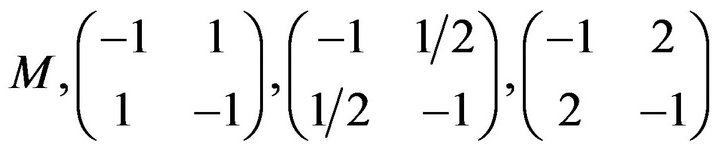 with refined inertias (0, 1, 1, 0), (0, 2, 0, 0) and (1, 1, 0, 0), respectively. It follows that
with refined inertias (0, 1, 1, 0), (0, 2, 0, 0) and (1, 1, 0, 0), respectively. It follows that 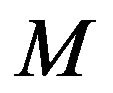 allows the only refined inertias (0, 1, 1, 0), (0, 2, 0, 0), (1, 1, 0, 0).
allows the only refined inertias (0, 1, 1, 0), (0, 2, 0, 0), (1, 1, 0, 0).
Lemma 2.3. Let 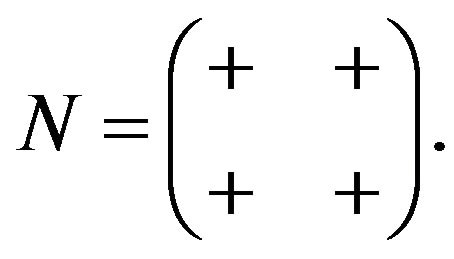 Then,
Then,  allows all refined inertias except (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2).
allows all refined inertias except (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2).
Proof. Since 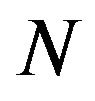 requires every realization with a positive trace, the refined inertias (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2) cannot be allowed by
requires every realization with a positive trace, the refined inertias (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2) cannot be allowed by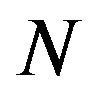 . Consider the following realizations of
. Consider the following realizations of ,
,
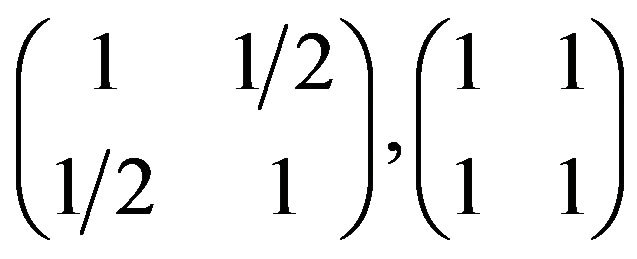 and
and 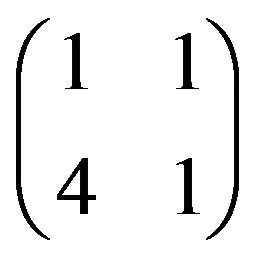 with refined inertias (20, 0, 0), (1, 0, 1, 0) and (1, 1, 0, 0), respectively. It follows that
with refined inertias (20, 0, 0), (1, 0, 1, 0) and (1, 1, 0, 0), respectively. It follows that  allows all refined inertias except (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2).
allows all refined inertias except (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2).
Lemma 2.4. Let  Then,
Then,  allows the refined inertia (0, 0, 0, 2).
allows the refined inertia (0, 0, 0, 2).
Proof. Lemma 2.4 follows from the fact that a realization of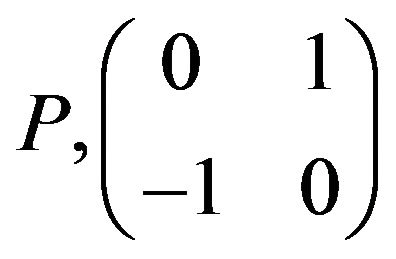 , has (0, 0, 0, 2) as its refined inertia.
, has (0, 0, 0, 2) as its refined inertia.
3. Minimal Critical Sets of Refined Inertias for Irreducible Sign Patterns of Order 2
We are now to identify all minimal critical sets of refined inertias for irreducible sign patterns of order 2.
Theorem 3.1. The set {(0, 0, 2, 0)} is the only minimal critical set with a single refined inertia for  ireducible sign patterns.
ireducible sign patterns.
Proof. Lemma 2.2 indicates that {(0, 2, 0, 0), {(1, 1, 0, 0)} and {(0, 1, 1, 0)} cannot be a minimal critical set of refined inertias. Lemma 2.3 indicates that {(2, 0, 0, 0)} and {(1, 0, 1, 0)} cannot be a minimal critical set of refined inertias. Lemma 2.4 indicates that {(0, 0, 0, 2)} cannot be a minimal critical set of refined inertias. So, it suffices to show that the set {(0, 0, 2, 0)} is a minimal critical sets of refined inertias.
If {(0, 0, 2, 0)} is allowed by an arbitrary irreducible sign pattern  of order 2, then all the main diagonal entries of
of order 2, then all the main diagonal entries of  must be nonzero. Since
must be nonzero. Since  allows a realization with a zero trace, the two diagonal entries of
allows a realization with a zero trace, the two diagonal entries of  are of opposite sign. That is to say, the associated digraph
are of opposite sign. That is to say, the associated digraph 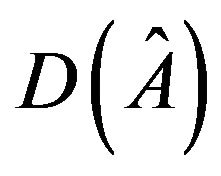 of
of , has a positive loop and a negative loop. For
, has a positive loop and a negative loop. For  allows a realization with zero determinant,
allows a realization with zero determinant,  has a negative 2-cycle. It follows from Lemma 2.1 that
has a negative 2-cycle. It follows from Lemma 2.1 that  is refined inertially arbitrary.
is refined inertially arbitrary.
Theorem 3.2. The refined inertia sets {(0, 0, 0, 2), (1, 0, 1, 0)}, {(0, 0, 0, 2), (0, 1, 1, 0)}, {(0, 0, 0, 2), (2, 0, 0, 0)}, {(0, 0, 0, 2), (0, 2, 0, 0)}, {(0, 0, 0, 2), (1, 1, 0, 0)}, {(1, 0, 1, 0), (0, 1, 1, 0)}, {(1, 0, 1, 0), (0, 2, 0, 0)}, {(1, 0, 1, 0), (2, 0, 0, 0)} and {(2, 0, 0, 0), (0, 2, 0, 0)} are minimal critical sets of refined inertias for irreducible sign patterns of order 2.
Proof. Let  be an arbitrary irreducible sign pattern of order 2. If {(0, 0, 0, 2), (1, 0, 1, 0)}
be an arbitrary irreducible sign pattern of order 2. If {(0, 0, 0, 2), (1, 0, 1, 0)}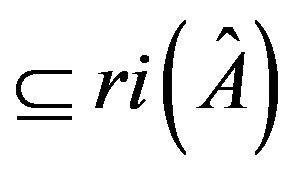 , then
, then  allows a realization with a positive trace and a realization with zero trace. It follows that
allows a realization with a positive trace and a realization with zero trace. It follows that 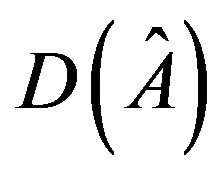 has a positive loop and a negative loop. Since
has a positive loop and a negative loop. Since  allows a realization with zero determinant,
allows a realization with zero determinant, 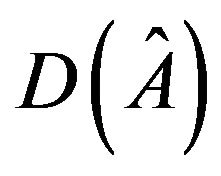 has a negative 2-cycle. By Lemma 2.1,
has a negative 2-cycle. By Lemma 2.1,  is refined inertially arbitrary and {(0, 0, 0, 2), (1, 0, 1, 0)} is a minimal critical set of refined inertias for
is refined inertially arbitrary and {(0, 0, 0, 2), (1, 0, 1, 0)} is a minimal critical set of refined inertias for 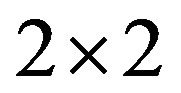 irreducible sign patterns. Similarly, we can show the refined inertias {(0, 0, 0, 2), (0, 1, 0)}, {(0, 0, 0, 2), (2, 0, 0, 0)}, {(0, 0, 0, 2), (0, 2, 0, 0)}, {(1, 0, 1, 0), (0, 1, 1, 0)}, {(1, 0, 1, 0), (0, 2, 0, 0)}, {(1, 0, 1, 0), (2, 0, 0, 0)} and {(2, 0, 0, 0), (0, 2, 0, 0)} are minimal critical sets of refined inertias for
irreducible sign patterns. Similarly, we can show the refined inertias {(0, 0, 0, 2), (0, 1, 0)}, {(0, 0, 0, 2), (2, 0, 0, 0)}, {(0, 0, 0, 2), (0, 2, 0, 0)}, {(1, 0, 1, 0), (0, 1, 1, 0)}, {(1, 0, 1, 0), (0, 2, 0, 0)}, {(1, 0, 1, 0), (2, 0, 0, 0)} and {(2, 0, 0, 0), (0, 2, 0, 0)} are minimal critical sets of refined inertias for 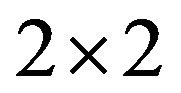 irreducible sign patterns.
irreducible sign patterns.
For the refined inertia set {(0, 0, 0, 2), (1, 1, 0, 0)} , we claim that the diagonal entries of
, we claim that the diagonal entries of  must be nonzero. In fact, assume that there exists at least a zero diagonal entry of
must be nonzero. In fact, assume that there exists at least a zero diagonal entry of . Then sign pattern
. Then sign pattern requires nonsingularity. It is contradicted that
requires nonsingularity. It is contradicted that allows two realizations with a positive and negative determinant, respectively. So, the diagonal entries of
allows two realizations with a positive and negative determinant, respectively. So, the diagonal entries of  must be nonzero. And the fact that the diagonal entries of
must be nonzero. And the fact that the diagonal entries of  are of opposite sign follows from that
are of opposite sign follows from that  allows a realization with a zero trace.
allows a realization with a zero trace. 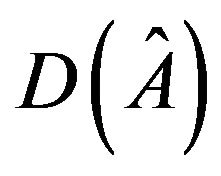 has a negative simple cycle of length 2 follows from that the inertia (0, 0, 0, 2)
has a negative simple cycle of length 2 follows from that the inertia (0, 0, 0, 2)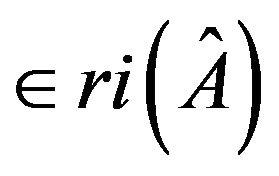 .
.
Next we identify all minimal critical sets of refined inertias for  irreducible sign patterns.
irreducible sign patterns.
Theorem 3.3. The sets {(0, 0, 2, 0)}, {(0, 0, 0, 2), (1, 0, 1, 0)}, {(0, 0, 0, 2), (0, 1, 1, 0)}, {(0, 0, 0, 2), (2, 0, 0, 0)}, {(0, 0, 0, 2), (0, 2, 0, 0)}, {(0, 0, 0, 2), (1, 1, 0, 0)}, {(1, 0, 1, 0), (0, 1, 1, 0)}, {(1, 0, 1, 0), (0, 2, 0, 0)}, {(1, 0, 1, 0), (2, 0, 0, 0)} and {(2, 0, 0, 0), (0, 2, 0, 0)} are the only minimal critical sets of refined inertias for 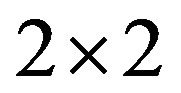 irreducible sign patterns.
irreducible sign patterns.
Proof. By Theorems 3.1 and 3.2, the refined inertia sets stated in Theorem 3.3 are minimal critical sets of refined inertias for  irreducible sign patterns. To show there exists no other minimal critical sets of refined inertias, it suffices to show that the remaining nine refined inertia sets with cardinality 2, {(1, 0, 1, 0), (2, 0, 0, 0)}, {(1, 0, 1, 0), (1, 1, 0, 0)}, {(2, 0, 0, 0), (1, 1, 0, 0)}, {(0, 1, 1, 0), (0, 2, 0, 0)}, {(0, 1, 1, 0), (1, 1, 0, 0)}, {(1, 1, 0, 0), (0, 2, 0, 0)} and the two refined inertia sets with cardinality 3, {(1, 0, 1, 0), (2, 0, 0, 0), (1, 1, 0, 0)} and {(0, 1, 1, 0), (0, 2, 0, 0), (1, 1, 0, 0)} are not critical sets of refined inertias. By Lemma 2.3, {(1, 0, 1, 0), (2, 0, 0, 0)}, {(1, 0, 1, 0), (1, 1, 0, 0)}, {(2, 0, 0, 0), (1, 1, 0, 0)} and {(1, 0, 1, 0), (2, 0, 0, 0)}, (1, 1, 0, 0)} are not critical sets of refined inertias. By Lemma 2.2, {(0, 1, 1, 0), (0, 2, 0, 0)}, {(0, 1, 1, 0), (1, 1, 0, 0)}, {(1, 1, 0, 0), (0, 2, 0, 0)} and {(0, 1, 1, 0), (0, 2, 0, 0)}, (1, 1, 0, 0)} are not critical sets of refined inertias.
irreducible sign patterns. To show there exists no other minimal critical sets of refined inertias, it suffices to show that the remaining nine refined inertia sets with cardinality 2, {(1, 0, 1, 0), (2, 0, 0, 0)}, {(1, 0, 1, 0), (1, 1, 0, 0)}, {(2, 0, 0, 0), (1, 1, 0, 0)}, {(0, 1, 1, 0), (0, 2, 0, 0)}, {(0, 1, 1, 0), (1, 1, 0, 0)}, {(1, 1, 0, 0), (0, 2, 0, 0)} and the two refined inertia sets with cardinality 3, {(1, 0, 1, 0), (2, 0, 0, 0), (1, 1, 0, 0)} and {(0, 1, 1, 0), (0, 2, 0, 0), (1, 1, 0, 0)} are not critical sets of refined inertias. By Lemma 2.3, {(1, 0, 1, 0), (2, 0, 0, 0)}, {(1, 0, 1, 0), (1, 1, 0, 0)}, {(2, 0, 0, 0), (1, 1, 0, 0)} and {(1, 0, 1, 0), (2, 0, 0, 0)}, (1, 1, 0, 0)} are not critical sets of refined inertias. By Lemma 2.2, {(0, 1, 1, 0), (0, 2, 0, 0)}, {(0, 1, 1, 0), (1, 1, 0, 0)}, {(1, 1, 0, 0), (0, 2, 0, 0)} and {(0, 1, 1, 0), (0, 2, 0, 0)}, (1, 1, 0, 0)} are not critical sets of refined inertias.
The following theorem follows directly for Theorem 3.3.
Theorem 3.4. Let  be a irreducible sign pattern of order 2. Then the following are equivalent:
be a irreducible sign pattern of order 2. Then the following are equivalent:
1)  is refined inertially arbitrary;
is refined inertially arbitrary;
2)  allows (0, 0, 2, 0);
allows (0, 0, 2, 0);
3)  allows (0, 0, 0, 2) and (1, 0, 1, 0);
allows (0, 0, 0, 2) and (1, 0, 1, 0);
4)  allows (0, 0, 0, 2) and (0, 1, 1, 0);
allows (0, 0, 0, 2) and (0, 1, 1, 0);
5)  allows (0, 0, 0, 2) and (2, 0, 0, 0);
allows (0, 0, 0, 2) and (2, 0, 0, 0);
6)  allows (0, 0, 0, 2) and (0, 2, 0, 0);
allows (0, 0, 0, 2) and (0, 2, 0, 0);
7)  allows (0, 0, 0, 2) and (1, 1, 0, 0);
allows (0, 0, 0, 2) and (1, 1, 0, 0);
8)  allows (1, 0, 1, 0) and (0, 1, 1, 0);
allows (1, 0, 1, 0) and (0, 1, 1, 0);
9)  allows (1, 0, 1, 0) and (0, 2, 0, 0);
allows (1, 0, 1, 0) and (0, 2, 0, 0);
10)  allows (1, 0, 1, 0) and (2, 0, 0, 0);
allows (1, 0, 1, 0) and (2, 0, 0, 0);
11)  allows (2, 0, 0, 0) and (0, 2, 0, 0).
allows (2, 0, 0, 0) and (0, 2, 0, 0).
4. Minimal Critical Sets of Inertias for Irreducible Sign Patterns of Order 2
In [6], all minimal critical sets of inertias for 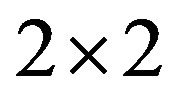 irreducible sign patterns, which are restated here as Theorem 4.1, have been identified. In this section, we present an alternative proof in terms of critial sets of refined inertias, as a by-product.
irreducible sign patterns, which are restated here as Theorem 4.1, have been identified. In this section, we present an alternative proof in terms of critial sets of refined inertias, as a by-product.
Theorem 4.1. The sets {(2, 0, 0), (0, 0, 2)}, {(0, 2, 0), (0, 0, 2)}, {(2, 0, 0), (0, 1, 1)}, {(0, 2, 0), (1, 0, 1)}, {(1, 1, 0), (0, 0, 2)}, {(1, 0, 1), (0, 0, 2)}, {(0, 1, 1), (0, 0, 2)}, {(2, 0, 0), (0, 2, 0)} and {(1, 0, 1), (0, 1, 1)} are the only minimal critical sets of inertias for  irreducible sign patterns.
irreducible sign patterns.
Proof. Note that an irreducible 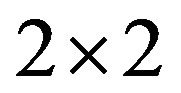 sign pattern:
sign pattern:
allows {(0, 0, 2), (2, 0, 0)} if and only if it allows
{(2, 0, 0, 0), (0, 0, 2, 0)} or {(2, 0, 0, 0), (0, 0, 0, 2)}allows {(0, 0, 2), (0, 2, 0)} if and only if it allows
{(0, 2, 0, 0), (0, 0, 2, 0)} or {(0, 2, 0, 0), (0, 0, 0, 2)}allows {(2, 0, 0), (0, 1, 1)} if and only if it allows
{(2, 0, 0, 0), (0, 1, 1, 0)}allows {(0, 2, 0), (1, 0, 1)} if and only if it allows
{(0, 2, 0, 0), (1, 0, 1, 0)}allows {(1, 1, 0), (0, 0, 2)} if and only if it allows
{(0, 0, 0, 2), (1, 1, 0, 0)} or {(0, 0, 2, 0), (1, 1, 0, 0)}allows {(1, 0, 1), (0, 0, 2)} if and only if it allows
{(0, 0, 0, 2), (1, 0, 1, 0)} or {(0, 0, 2, 0), (1, 0, 1, 0)}allows {(0, 1, 1), (0, 0, 2)} if and only if it allows
{(0, 0, 0, 2), (0, 1, 1, 0)} or {(0, 0, 2, 0), (0, 1, 1, 0)}allows {(2, 0, 0), (0, 2, 0)} if and only if it allows
{(2, 0, 0, 0), (0, 2, 0, 0)}allows {(1, 0, 1), (0, 1, 1)} if and only if it allows
{(0, 1, 1, 0), (1, 0, 1, 0)}.
Since all of the refined inertia sets above are critical sets of refined inertias (not necessarily minimal), the above sets of inertias are critical sets, and indeed are also easily seen to be minimal (since at least one of the corresponding sets of refined inertias is minimal in each case). It follows that the above sets of inertias are the only minimal critical sets of inertias because the corresponding sets of refined inertias are the only minimal critical sets of refined inertias.
5. Concluding Remarks
We have identified all minimal critical sets of refined inertias for irreducible sign patterns of order 2. As a by-product, all minimal critical sets of inertias for irreducible sign patterns of order 2 have also been identified in a new proof. In a follow-up paper, we will consider other cases, e.g.,  , though identification of all critical sets of inertias for irreducible sign patterns of order
, though identification of all critical sets of inertias for irreducible sign patterns of order  has been posed as an open question in [6].
has been posed as an open question in [6].
6. Acknowledgements
The authors would like to express their great gratitude to the referees and editor for their constructive comments and suggestions that led to the enhancement of this paper. This research was supported in part by the Sci. & Tech. Research Fund of Huaiyin Institute of Technology (HGB1111), National Natural Science Foundation of China (11201168) and Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (Grant No. 12KJB110001).
REFERENCES
- F. Hall and Z. Li, “Sign Pattern Matrices,” In: L. Hogben, Ed., Handbook of Linear Algebra, Chapman & Hall/CRC Press, Boca Ration, 2007.
- R. A. Horn and C. R. Johnson, “Matrix Analysis,” Cambridge University Press, New York, 1985. doi:10.1017/CBO9780511810817
- L. Deaett, D. D. Olesky and P. van den Driessche, “Refined Inertially and Spectrally Arbitrary Zero-Nonzero Patterns,” The Electronic Journal of Linear Algebra, Vol. 20, 2010, pp. 449-467.
- M. S. Cavers and K. N. Vander Meulen. “Spectrally and Inertially Arbitrary Sign Patterns,” Linear Algebra and Its Applications, Vol. 394, No. 1, 2005, pp. 53-72. doi:10.1016/j.laa.2004.06.003
- M. S. Cavers, K. N. Meulen and L. Vanderspek. “Sparse Inertially Arbitrary Patterns,” Linear Algebra and Its Applications, Vol. 431, No. 11, 2009, pp. 2024-2034. doi:10.1016/j.laa.2009.06.040
- I. J. Kim, D. D. Olesky and P. van den Driessche, “Critical Sets of Inertias for Matrix Patterns,” Linear and Multilinear Algebra, Vol. 57, No. 3, 2009, pp. 293-306. doi:10.1080/03081080701616672
- B. L. Yu, T. Z. Huang, J. Luo and H. B. Hua, “Critical Sets of Refined Inertias for Irreducible Zero-Nonzero Patterns of Orders 2 and 3,” Linear Algebra and Its Applications, Vol. 437, No. 2, 2012, pp. 490-498. doi:10.1016/j.laa.2012.03.007

