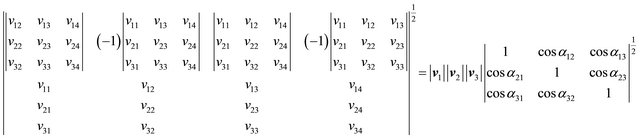Advances in Linear Algebra & Matrix Theory
Vol.3 No.1(2013), Article ID:29071,6 pages DOI:10.4236/alamt.2013.31001
Geometric Analogy and Products of Vectors in n Dimensions
UniFOA—Centro Universitário de Volta Redonda, Volta Redonda, Brazil
Email: simal.leonardo@terra.com.br, leonardo.moreira@foa.org.br
Received November 12, 2012; revised December 21, 2012; accepted December 30, 2012
Keywords: Cross Product; Space IRn; Determinants; Geometric Analogy; Eckman’s Product
ABSTRACT
The cross product in Euclidean space IR3 is an operation in which two vectors are associated to generate a third vector, also in space IR3. This product can be studied rewriting its basic equations in a matrix structure, more specifically in terms of determinants. Such a structure allows extending, for analogy, the ideas of the cross product for a type of the product of vectors in higher dimensions, through the systematic increase of the number of rows and columns in determinants that constitute the equations. So, in a n-dimensional space with Euclidean norm, we can associate n – 1 vectors and to obtain an n-th vector, with the same geometric characteristics of the product in three dimensions. This kind of operation is also a geometric interpretation of the product defined by Eckman [1]. The same analogies are also useful in the verification of algebraic properties of such products, based on known properties of determinants.
1. Introduction
In the Euclidean space , the cross product of two vectors
, the cross product of two vectors  and
and 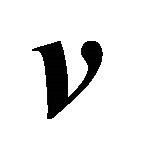 is the vector designated by the symbol
is the vector designated by the symbol , and defined for the following conditions [2]:
, and defined for the following conditions [2]:
a) The norm of vector , symbolized for
, symbolized for , is given for
, is given for
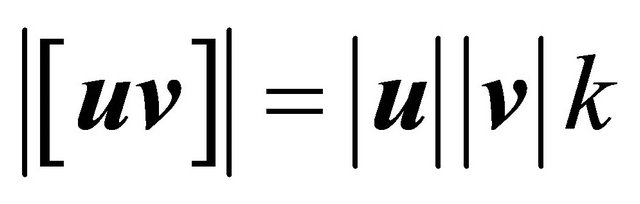 , (1)
, (1)
where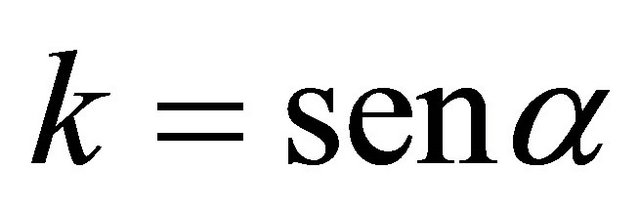 , being
, being  the angle between the vectors
the angle between the vectors  and
and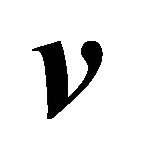 .
.
b) The vector  is perpendicular simultaneously to the vectors
is perpendicular simultaneously to the vectors  and
and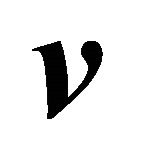 :
:
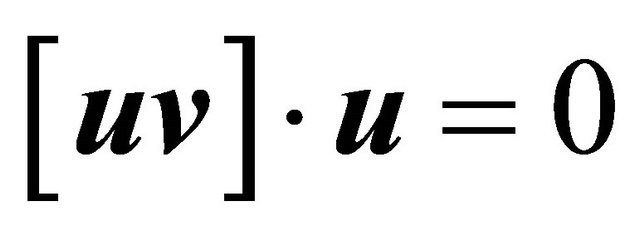 , (2)
, (2)
 . (3)
. (3)
As a consequence of b),  is the normal vector to the plane defined for the vectors
is the normal vector to the plane defined for the vectors  and
and  (Figure 1), if these are linearly independent vectors. Considering
(Figure 1), if these are linearly independent vectors. Considering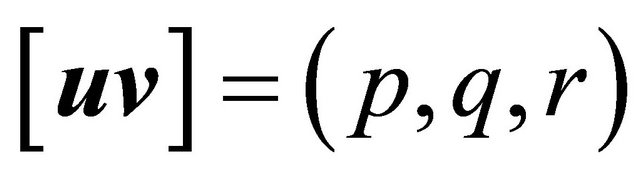 , then
, then , where
, where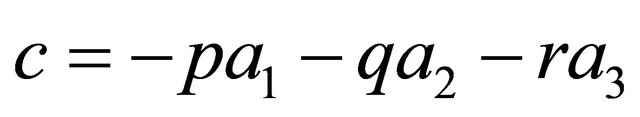 , represents the equation of the plane
, represents the equation of the plane  in a Cartesian coordinate system (
in a Cartesian coordinate system (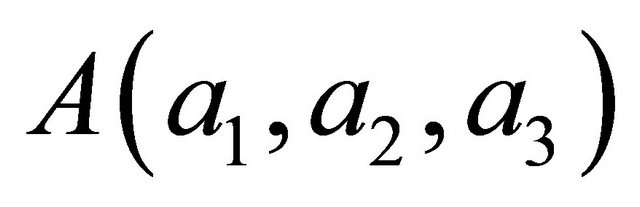 is a point in
is a point in  and
and ).
).
If  and
and  are linearly dependent vectors, then
are linearly dependent vectors, then
 , (4)
, (4)
where the symbol 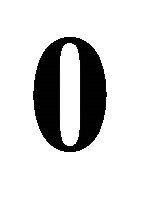 represents the null vector.
represents the null vector.
c) The vector  is oriented in relation to the vectors
is oriented in relation to the vectors  and
and 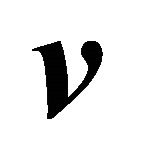 just as, in right-handed coordinate system, the z-axis it is oriented in relation to the x-axis and y-axis.
just as, in right-handed coordinate system, the z-axis it is oriented in relation to the x-axis and y-axis.
d) The volume V3 of parallelepiped defined for the vectors ,
,  and
and  is the square of the number
is the square of the number 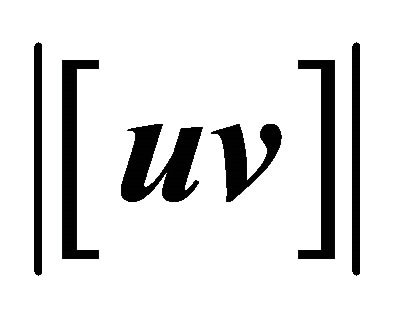 (Figure 2):
(Figure 2):
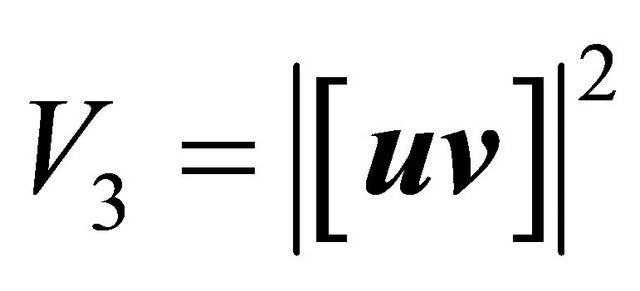 (5)
(5)
The equalities (2), (3) and (5) are equivalent to those given in a Definition 1 found in [3].
In this paper, it is shown that it is possible, through simple analogies with the case in the space , to extend the ideas of the cross product to the space
, to extend the ideas of the cross product to the space , and more generally, to the space
, and more generally, to the space . The characteristics of the cross product in
. The characteristics of the cross product in  are maintained in higher dimensions.
are maintained in higher dimensions.
2. Matrix Structure of 
The initial reasoning for the extension of the ideas of the cross product is the fact that their basic expressions can be represented in the form of determinants.
In an orthogonal coordinate system, representing the vectors  and
and 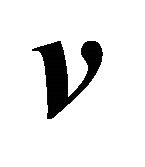 in terms of 3-tuples
in terms of 3-tuples 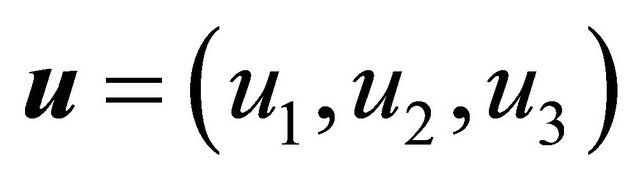 and
and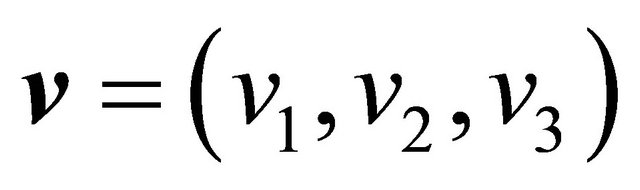 , the vector
, the vector  can be obtained starting from the development of the symbolic determinant
can be obtained starting from the development of the symbolic determinant
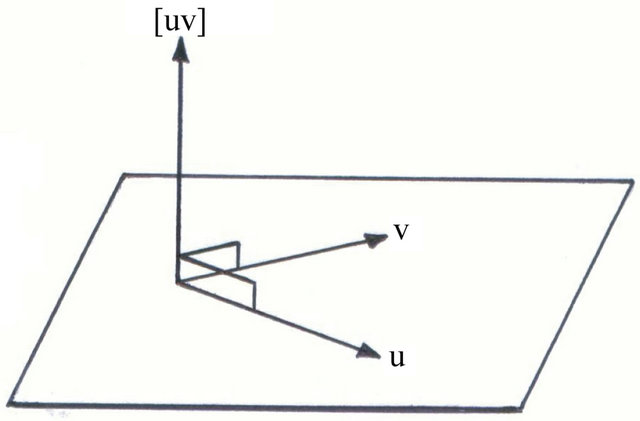
Figure 1. [uv] is the normal vector to the plane defined for the vectors u and v.

Figure 2. Parallelepiped defined for the vectors u, v and [uv].
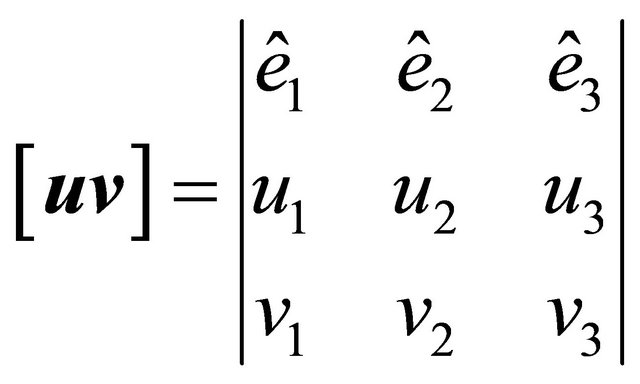 , (6)
, (6)
where 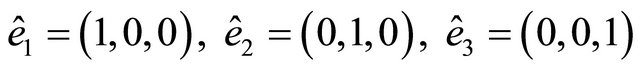 are the vectors of orthonormal basis in
are the vectors of orthonormal basis in .
.
The development of the Equation (6) leads to the vector form:
 , (7)
, (7)
and the norm of vector  is calculated with the definition of Euclidean norm, resulting in
is calculated with the definition of Euclidean norm, resulting in
 , (8)
, (8)
an equivalent format to
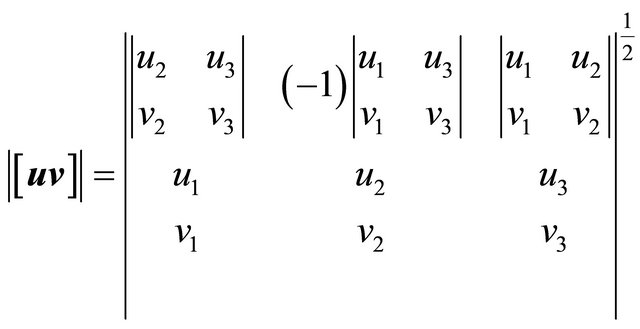 . (9)
. (9)
In Equation (1),
 , (10)
, (10)
and combining the Equations (9) and (10), we obtain
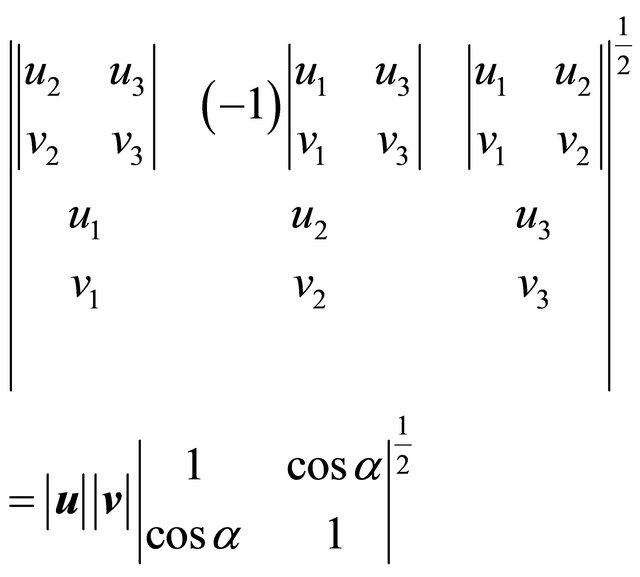 (11)
(11)
Equation (11) will be used as starting point for the analogies developed in the remaining of this work.
3. Extension of the Cross Product to the Euclidean Space IR4
Consider three vectors in Euclidean space , represented in terms of quadruples
, represented in terms of quadruples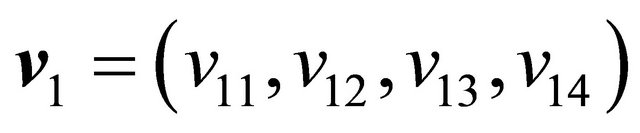 ,
,
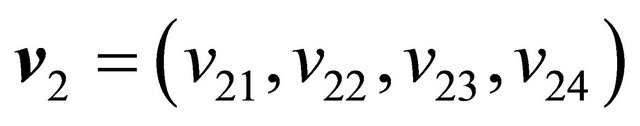 and
and . Let
. Let
 and
and
 be the vectors of orthonormal basis in
be the vectors of orthonormal basis in .
.
It is possible to develop an equivalent product to (1), through simple extension of ideas and increase of dimensions. In space , two vectors
, two vectors  and
and 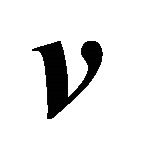 generate a third vector whose norm is proportional to the product of the norms of the generating vectors, being the proportionality constant related to the angle between
generate a third vector whose norm is proportional to the product of the norms of the generating vectors, being the proportionality constant related to the angle between  and
and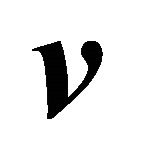 . In space
. In space , three vectors
, three vectors 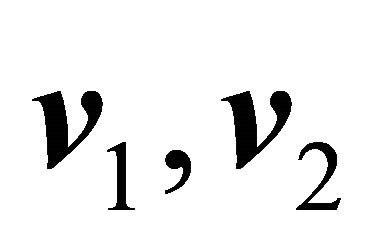 and
and  generate a fourth vector whose norm is proportional to the product of the norms of the generating vectors, being the proportionality constant related to the angles between the vectors
generate a fourth vector whose norm is proportional to the product of the norms of the generating vectors, being the proportionality constant related to the angles between the vectors 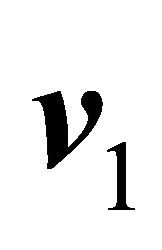 and
and 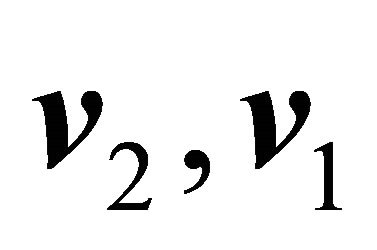 and
and 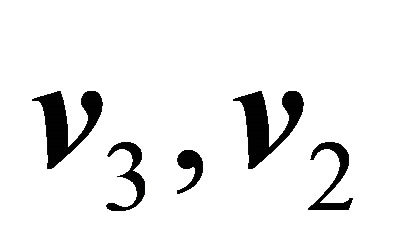 and
and .
.
In symbolic terms, this product of vectors in Euclidean space  is obtained from the development of the determinant
is obtained from the development of the determinant
 , (12)
, (12)
so that
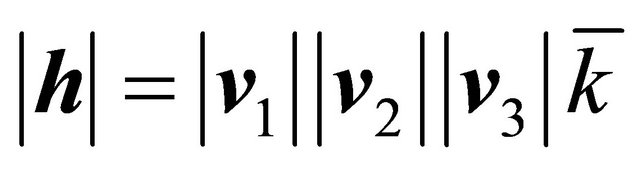 , (13)
, (13)
with
 (14)
(14)
and the conditions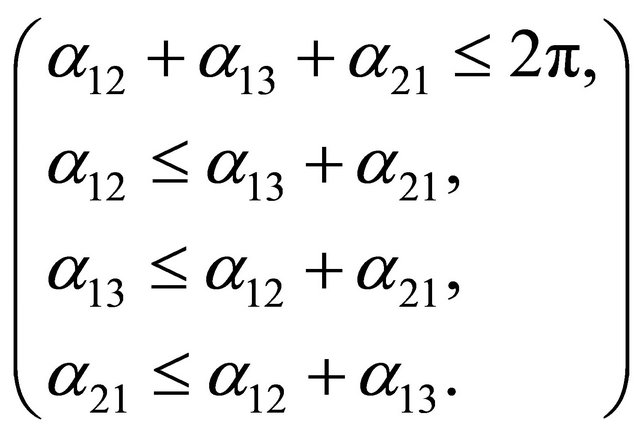 .
.
The equal sign in the conditions on the angles, given in (14), is justified for the case of coplanar vectors.
In Equation (14),  represents the angle between two of the generating vectors of
represents the angle between two of the generating vectors of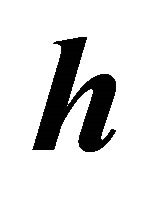 , and naturally
, and naturally , so that
, so that 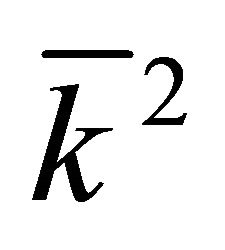 is the determinant of a symmetric matrix.
is the determinant of a symmetric matrix.
The equivalent in space  of Equation (11) is (see the Equation (15) below):
of Equation (11) is (see the Equation (15) below):
The characteristics of the product  in space
in space  are conserved for
are conserved for  in space
in space :
:
a) The norm of 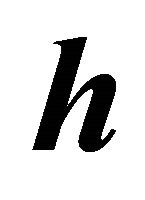 is proportional to the product
is proportional to the product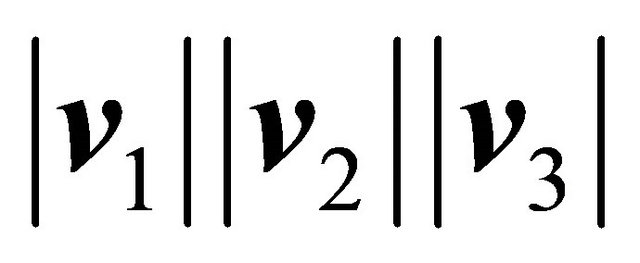 . It is sufficient to develop the determinants in Equation (15) to verify the identity.
. It is sufficient to develop the determinants in Equation (15) to verify the identity.
b) The vector  is perpendicular to each one of the vectors
is perpendicular to each one of the vectors 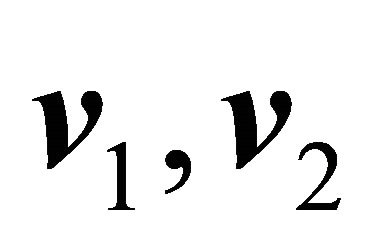 and
and . The term “perpendicular” should be interpreted here as only in the sense that the scalar product
. The term “perpendicular” should be interpreted here as only in the sense that the scalar product 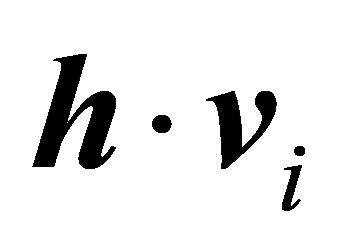 results null.
results null.
PROOF: The elements of the 1st row of the determinant that represents the norm of 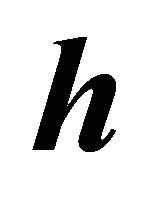 are the same values as their own cofactors. It is known that the sum of the products of the elements of a row for the cofactors of the elements corresponding of other row (inner product) in a determinant results in zero (Cauchy’s Determinant Theorem), that is,
are the same values as their own cofactors. It is known that the sum of the products of the elements of a row for the cofactors of the elements corresponding of other row (inner product) in a determinant results in zero (Cauchy’s Determinant Theorem), that is, .
.
It is also noted that  is the normal vector to the hyperplane that contains
is the normal vector to the hyperplane that contains 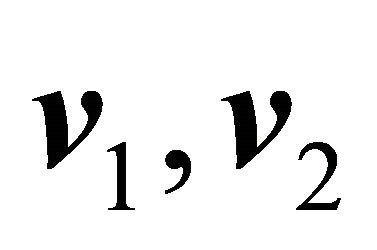 and
and . Being
. Being
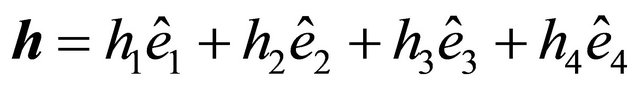 , then
, then
 , where
, where
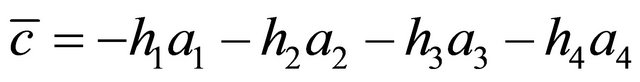 , represents the Cartesian equation of hyperplane
, represents the Cartesian equation of hyperplane 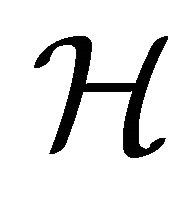 (
(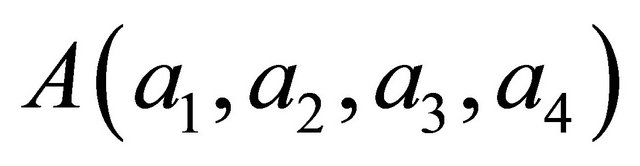 is a point in
is a point in  and
and ).
).
c) The vector  is oriented in relation to the vectors
is oriented in relation to the vectors 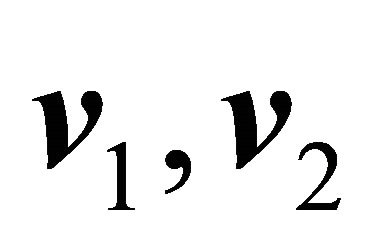 and
and  just as the vector
just as the vector 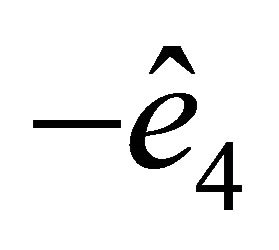 in relation to
in relation to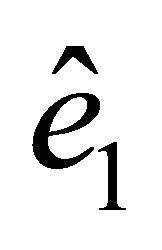 ,
, 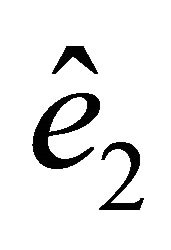 and
and .
.
d) The content of parallelotope defined for the vectors 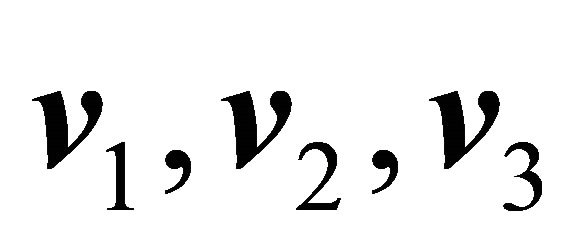 and
and  is the square of number
is the square of number .
.
PROOF: With effect, the determinant to the left in Equation (15) represents the number . In this way,
. In this way, 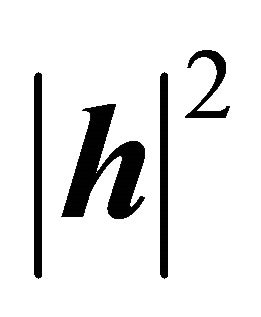 is the determinant whose rows are formed by the vectors
is the determinant whose rows are formed by the vectors 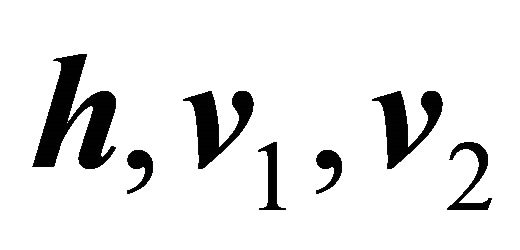 and
and , representing the content of parallelotope (4-parallelepiped) that has the four vectors as edges linearly independents [4].
, representing the content of parallelotope (4-parallelepiped) that has the four vectors as edges linearly independents [4].
4. Product of n − 1 Vectors in Euclidean space IRn
Consider n − 1 vectors in Euclidean space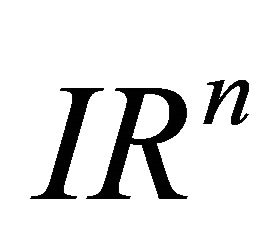 , represented in terms of n-tuples, such that
, represented in terms of n-tuples, such that
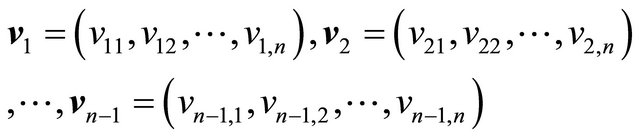
The product  in space
in space  is a vector perpendicular simultaneously to all the
is a vector perpendicular simultaneously to all the
 and whose norm is given by the formula
and whose norm is given by the formula
 , (16)
, (16)
with
 . (17)
. (17)
It is observed that this form is equivalent to the products of vectors defined by [1], and cited in [5,6], namely (using the same symbols as in [6]), that a cross product satisfies the axioms:
(A1)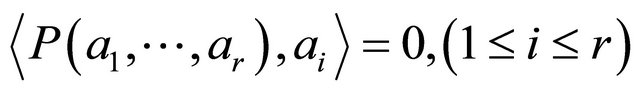 ,
,
(A2)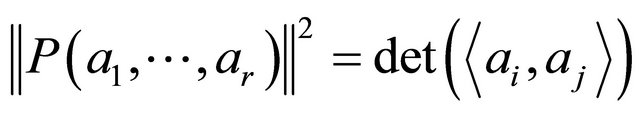 where
where .
.
These preliminary definitions can be formalized starting from the following proposition.
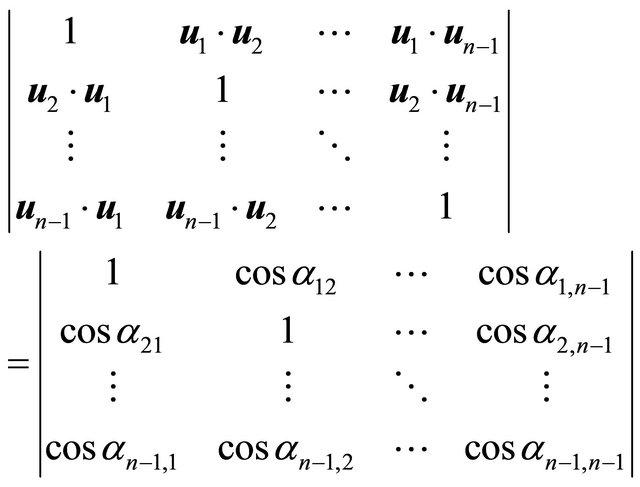
PROPOSITION: Let n − 1 vectors be in space , with inner product and Euclidean norm. Consider also that the vectors are represented by n-tuples such that
, with inner product and Euclidean norm. Consider also that the vectors are represented by n-tuples such that

Being  the angle between the i-th vector
the angle between the i-th vector  and the j-th vector
and the j-th vector , the following equality is true (see the Equation (18) below):
, the following equality is true (see the Equation (18) below):
|
(15) |
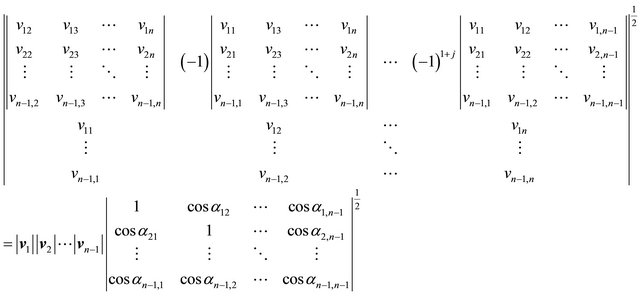 (18)
(18)
PROOF: Consider n − 1 unit vectors 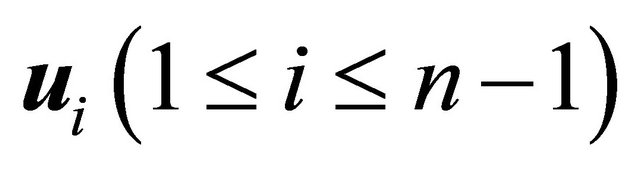 in space IRn, with inner product and Euclidean norm. Consider also that each ui represents the unit vector in the same direction of vi given in the Equation (18), so that
in space IRn, with inner product and Euclidean norm. Consider also that each ui represents the unit vector in the same direction of vi given in the Equation (18), so that
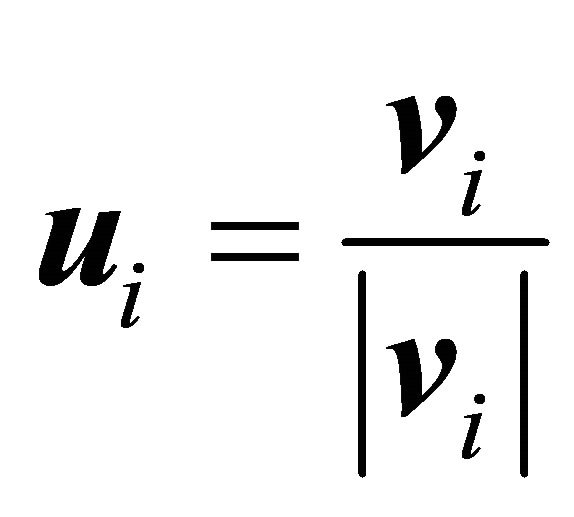 . (19)
. (19)
If the unit vectors are represented by n-tuples such that
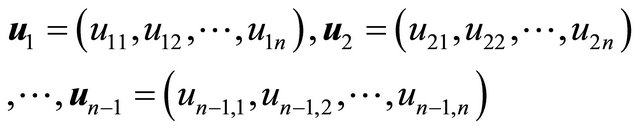 being
being 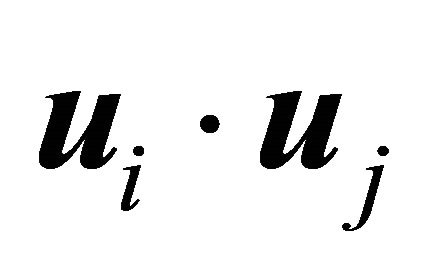 the inner product between the i-th unit vector
the inner product between the i-th unit vector  and the j-th unit vector
and the j-th unit vector , can be grouped, based on the properties presented in (A2), the components of
, can be grouped, based on the properties presented in (A2), the components of  in the following identity, which is true for values of
in the following identity, which is true for values of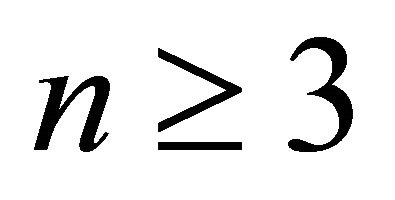 :
:
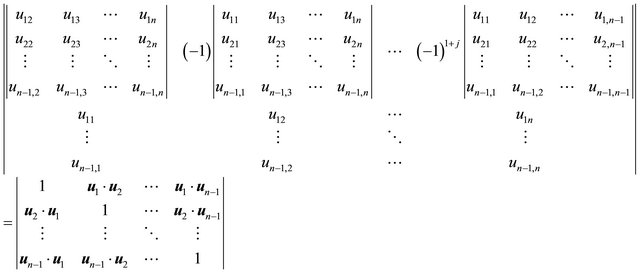 (20)
(20)
Starting from Equation (20), Equation (18) can be demonstrated. With effect, multiplying both members of (20) for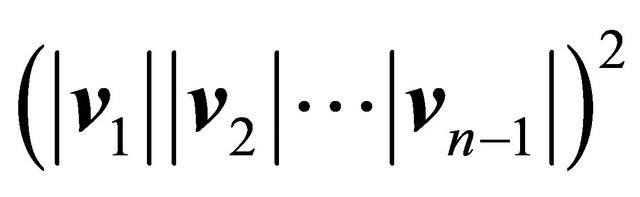 , the determinant to the left will have their rows orderly and appropriately multiplied by each one of
, the determinant to the left will have their rows orderly and appropriately multiplied by each one of , and since
, and since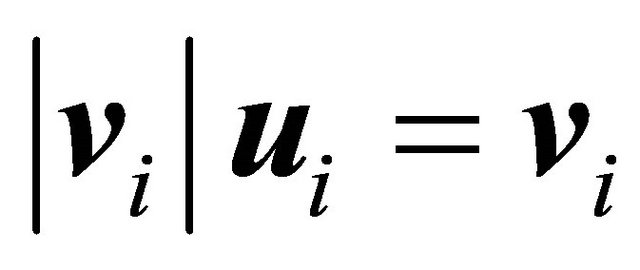 , is obtained the corresponding determinant of Equation (18).
, is obtained the corresponding determinant of Equation (18).
Representing, for convenience,
 (21)
(21)
we have that:
 . (22)
. (22)
In relation to the determinant to the right in Equation (20), it is sufficient to observe that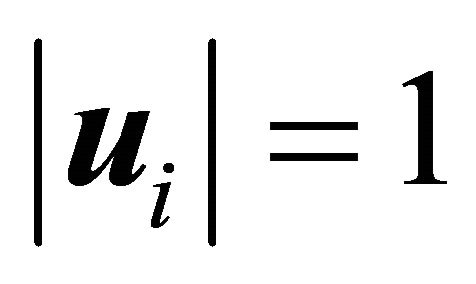 , therefore
, therefore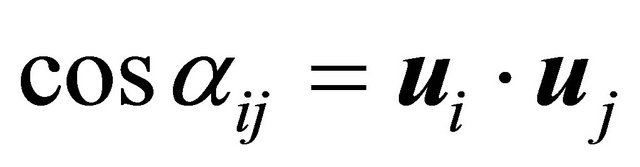 , that is:
, that is:
 (23)
(23)
With such considerations, it is demonstrated that
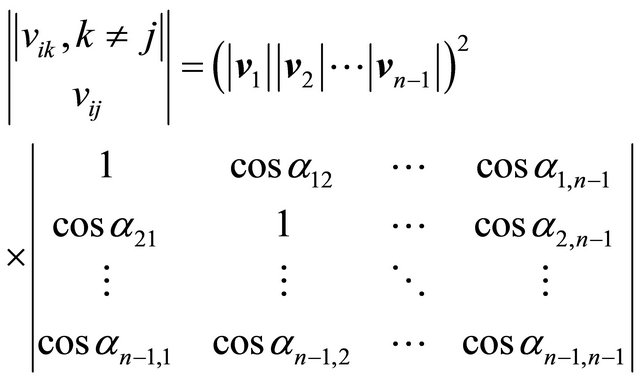 , (24)
, (24)
and the square root of Equation (23) shows that Equation (18) is true.
Equation (18) is the equivalent n-dimensional of the Equations (11) and (15), validating the extension of cross product. The geometric properties of  are conserved in n dimensions:
are conserved in n dimensions:
a) The norm of  is proportional to the product
is proportional to the product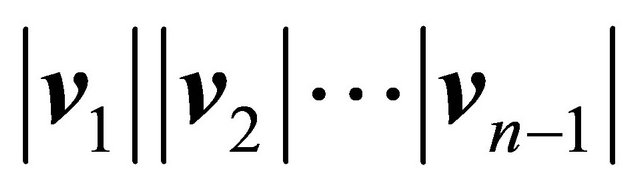 , being the proportionality constant K associated to the angles between the vectors
, being the proportionality constant K associated to the angles between the vectors .
.
PROOF: The proof consists of the own demonstration of the Equation (18).
b) The vector  is “perpendicular” to each one of the vectors
is “perpendicular” to each one of the vectors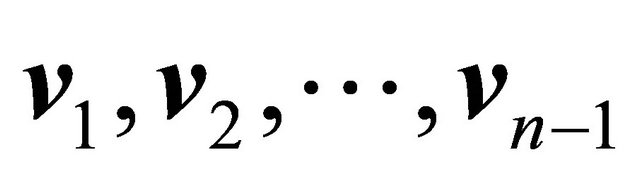 .
.
PROOF: The elements of the 1st row of the determinant that represents the norm of  are the same values as their own cofactors. In agreement with Cauchy’s Determinant Theorem, the sum of the products of the elements of a row for the cofactors of the elements corresponding of another row (inner product) in a determinant results in zero, that is,
are the same values as their own cofactors. In agreement with Cauchy’s Determinant Theorem, the sum of the products of the elements of a row for the cofactors of the elements corresponding of another row (inner product) in a determinant results in zero, that is,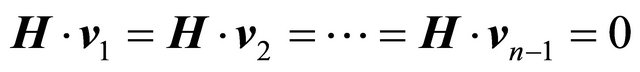 .
.
It is also noted that  is the normal vector to the hyperplane that contains
is the normal vector to the hyperplane that contains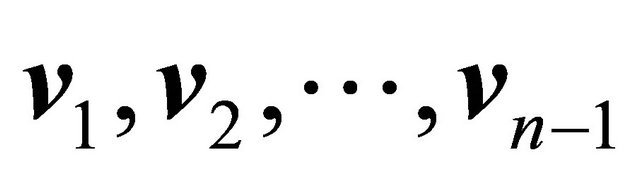 . Being
. Being
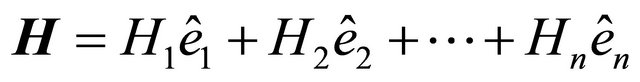 , then
, then
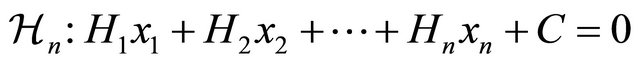 , where
, where
 , represents the Cartesian equation of hyperplane
, represents the Cartesian equation of hyperplane  (
( is a point in
is a point in 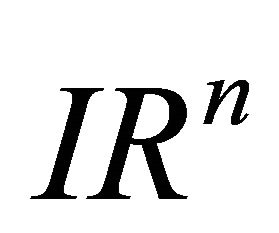 and
and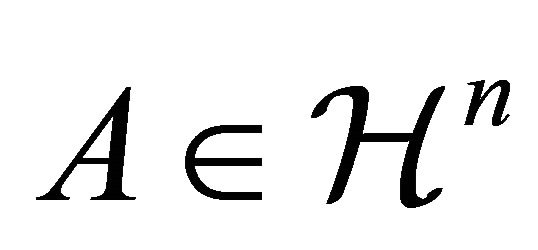 ).
).
c) The vector  is oriented in relation to the vectors
is oriented in relation to the vectors  just as the vector
just as the vector 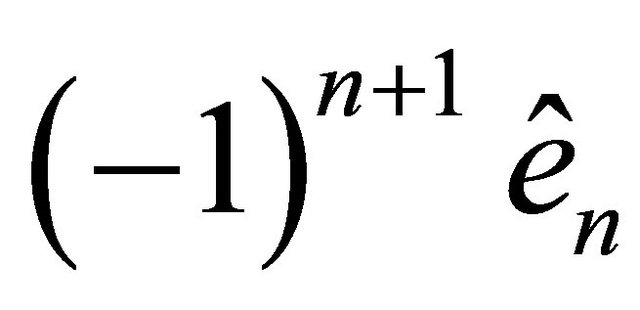 is oriented in relation to
is oriented in relation to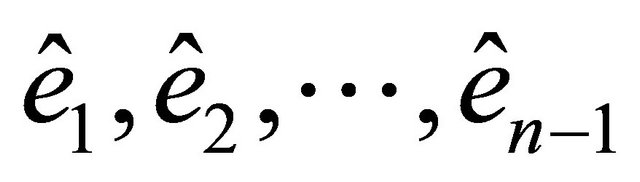 .
.
d) The content of parallelotope defined for the vectors 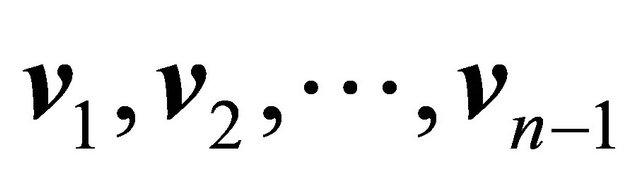 and
and  is the square of number
is the square of number .
.
PROOF: The determinant to the left in Equation (18) represents the number . In this way,
. In this way, 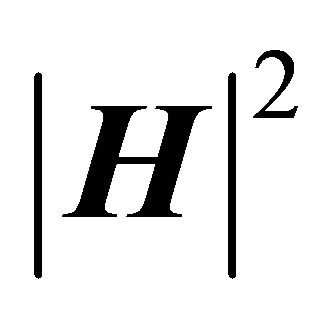 is the determinant whose rows are formed by the vectors
is the determinant whose rows are formed by the vectors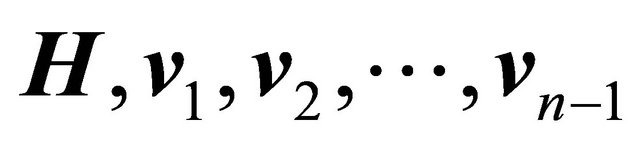 , representing the content of parallelotope (n-parallelepiped) that has the n vectors as edges linearly independents [4].
, representing the content of parallelotope (n-parallelepiped) that has the n vectors as edges linearly independents [4].
5. Conclusions
The possibility to represent the equations of the definition of cross product in the space  in terms of determinants allows the extension of the concept of the product of vectors for higher dimensions, systematically increasing rows and columns to the determinants.
in terms of determinants allows the extension of the concept of the product of vectors for higher dimensions, systematically increasing rows and columns to the determinants.
Through basic properties of determinants, it is shown that the characteristics of the cross product are conserved in n dimensions, for any value of n, since such properties are not modified by the increment or decrease of rows and columns to these determinants.
Other geometric properties can be verified, as the relationship between the cross product and area, because just as the number  is related to areas of triangles and parallelograms, the number
is related to areas of triangles and parallelograms, the number  is related to contents of simplex and parallelotopes, in an equivalent way to Cayley-Menger determinant [7,8].
is related to contents of simplex and parallelotopes, in an equivalent way to Cayley-Menger determinant [7,8].
Although this work has given emphasis to the geometric properties of the product of vectors in the space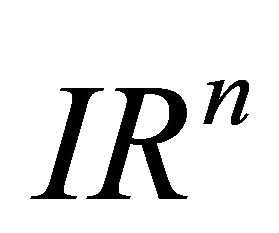 , it indirectly shows that their algebraic properties are also similar to those valid ones in space
, it indirectly shows that their algebraic properties are also similar to those valid ones in space , for instance:
, for instance:
(C1) If 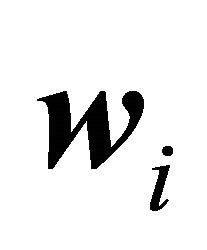 is any vector in space
is any vector in space 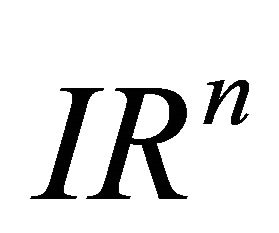 for
for , then a)
, then a) ;
;
b)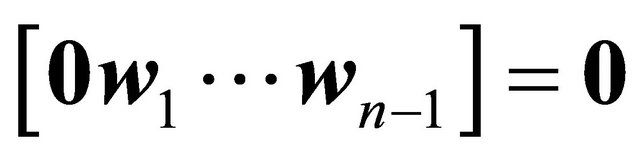 ;
;
c)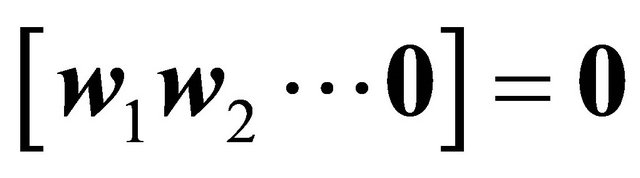 ;
;
d)  if any of vectors
if any of vectors 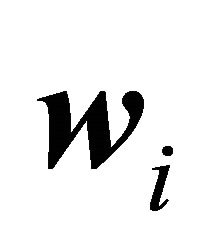 is the null vector.
is the null vector.
(C2) The position change among two vectors in the product 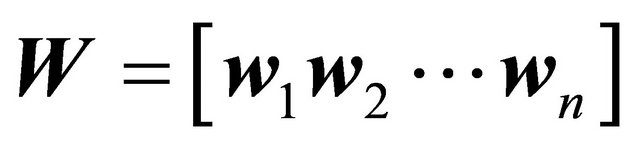 results in the vector
results in the vector .
.
(C3) If  is any vector in space
is any vector in space 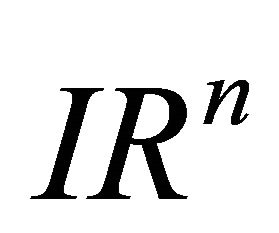 for
for 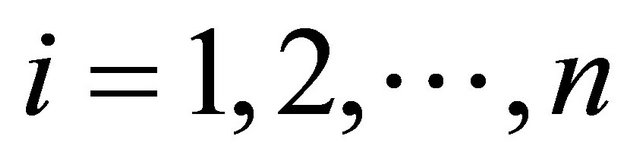 , and
, and , then a)
, then a) ;
;
b)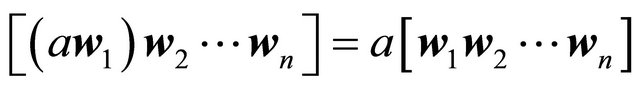 .
.
These and other algebraic properties, including the distributive property of the product in relation to the sum of vectors, are verified easily by the application of the convenient rules on determinants to the matrix structure of product of vectors.
The analogies developed appear still for the possibility of new extensions associated to the concept of products of vectors, such as eventual developments that are related to a type of equivalent n-dimensional of the concept of curl, for example.
REFERENCES
- B. Eckmann, “Stetige Lösungen Linearer Gleichungssysteme,” Commentarii Mathematici Helvetici, Vol. 15, 1943, pp. 318-339. doi:10.1007/BF02565648
- N. Efimov, “Elementos de Geometria Analítica,” Cultura Brasileira, São Paulo, 1972.
- A. Elduque, “Vector Cross Products,” Talk Presented at the Seminario Rubio de Francia of the Universidad de Zaragoza on April 1 2004.
- S. Lipschutz and M. Lipson, “Álgebra Linear,” Bookman, Porto Alegre, 2008.
- R. Brown and A. Gray, “Vector Cross Products,” Commentarii Mathematici Helvetici, Vol. 42, 1967, pp. 222- 236. doi:10.1007/BF02564418
- A. Gray, “Vector Cross Products on Manifolds,” University of Maryland, College Park, 1968.
- P. Gritzmann and V. Klee, “On the Complexity of Some Basic Problems in Computational Convexity II. Volume and Mixed Volumes,” In: T. Bisztriczky, P. McMuffen, R. Schneider and A. W. Weiss, Eds., Polytopes: Abstract, Convex and Computational, Kluwer, Dordrecht, 1994, p. 29.
- D. M. Y. Sommerville, “An Introduction to the Geometry of n Dimensions,” Dover, New York, 1958, p. 124.