Advances in Linear Algebra & Matrix Theory
Vol.2 No.3(2012), Article ID:22660,6 pages DOI:10.4236/alamt.2012.23004
A New Iterative Solution Method for Solving Multiple Linear Systems
Department of Mathematics, Persian Gulf University, Bushehr, Iran
Email: karimi@pgu.ac.ir
Received July 25, 2012; revised August 25, 2012; accepted September 8, 2012
Keywords: Iterative Method; Multiple Linear Systems; LSQR Method; GL-LSQR Method; Projection Method
ABSTRACT
In this paper, a new iterative solution method is proposed for solving multiple linear systems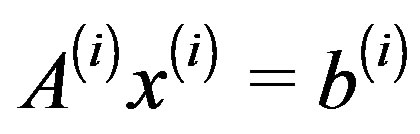 , for
, for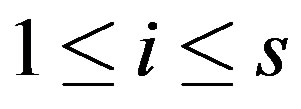 , where the coefficient matrices
, where the coefficient matrices 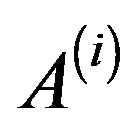 and the right-hand sides
and the right-hand sides 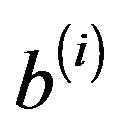 are arbitrary in general. The proposed method is based on the global least squares (GL-LSQR) method. A linear operator
are arbitrary in general. The proposed method is based on the global least squares (GL-LSQR) method. A linear operator 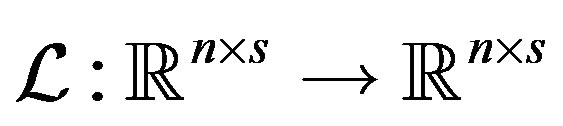 is defined to connect all the linear systems together. To approximate all numerical solutions of the multiple linear systems simultaneously, the GL-LSQR method is applied for the operator
is defined to connect all the linear systems together. To approximate all numerical solutions of the multiple linear systems simultaneously, the GL-LSQR method is applied for the operator 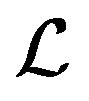 and the approximate solutions are obtained recursively. The presented method is compared with the well-known LSQR method. Finally, numerical experiments on test matrices are presented to show the efficiency of the new method.
and the approximate solutions are obtained recursively. The presented method is compared with the well-known LSQR method. Finally, numerical experiments on test matrices are presented to show the efficiency of the new method.
1. Introduction
We want to solve, using global least squares (GL-LSQR) method, the following linear systems:
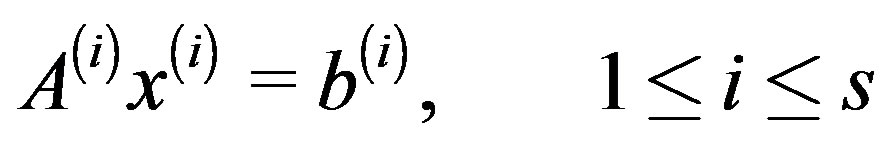 (1)
(1)
where 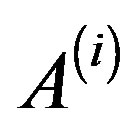 are arbitrary matrices of order n, and in general
are arbitrary matrices of order n, and in general 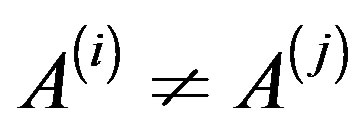 and
and 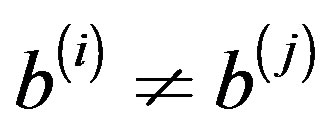 for
for 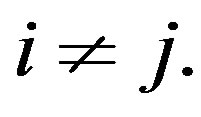 In spite of that, in many practical application the coefficient matrices and the right-hand sides are not arbitrary, and often there is information that can be shared among the coefficient matrices and right-hand sides. Multiple linear systems (1) arise in many problems in scientific computing and engineering application, including recursive least squares computations [1,2], wave scattering problems [3,4], numerical methods for integral equations [4,5], and image restorations [6].
In spite of that, in many practical application the coefficient matrices and the right-hand sides are not arbitrary, and often there is information that can be shared among the coefficient matrices and right-hand sides. Multiple linear systems (1) arise in many problems in scientific computing and engineering application, including recursive least squares computations [1,2], wave scattering problems [3,4], numerical methods for integral equations [4,5], and image restorations [6].
Many authors, see [7,8], have researched to approximate the solutions of the multiple linear systems (1) with the same coefficient matrix but different right-hand sides, i.e.,
 (2)
(2)
Recently, S. Karimi and F. Toutounian proposed an iterative method for solving the linear systems (2) with the some advantages over the existing methods, see [9- 11], for more details. In [12], Tony F. chan and Michael K. Ng presented the Galerkin projection method for solving linear systems (1). They focused on the seed projection method which generates a Krylov subspace from a set of direction vectors obtained by solving one of the systems, called the seed system, by the CG method and then projects the residuals of other systems onto the generated Krylov subspace to get the approximate solutions. Note that the coefficient matrices in this method are real symmetric positive definite.
In this paper, we propose a new method to solve the linear systems (1) simultaneously, where the coefficient matrices and right-hand sides are arbitrary. We define a linear operator 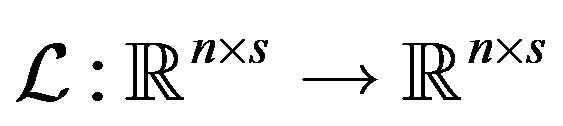 to connect all the linear systems (1) together. Then we apply the GL-LSQR method [13] for the linear operator
to connect all the linear systems (1) together. Then we apply the GL-LSQR method [13] for the linear operator 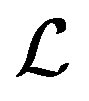 and obtain recursively the approximate solutions simultaneously. In the new method , the linear operator
and obtain recursively the approximate solutions simultaneously. In the new method , the linear operator 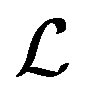 will be reduced to a lower global bidiagonal, namely
will be reduced to a lower global bidiagonal, namely 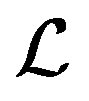 -Bidiag, matrix form. We obtain a recurrence formula for generating the sequence of approximate solutions. Our new method has certain advantages over the existent methods. In the new method, the coefficient matrices
-Bidiag, matrix form. We obtain a recurrence formula for generating the sequence of approximate solutions. Our new method has certain advantages over the existent methods. In the new method, the coefficient matrices 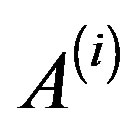 and right-hand sides
and right-hand sides 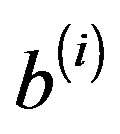 are arbitrary. Also we do not need to store the basis vectors, we do not need to predetermine a subspace dimension and the approximate solutions and residuals are cheaply computed at every stage of the algorithm because they are updated with short-term recurrence.
are arbitrary. Also we do not need to store the basis vectors, we do not need to predetermine a subspace dimension and the approximate solutions and residuals are cheaply computed at every stage of the algorithm because they are updated with short-term recurrence.
The remainder of the paper is organized as follows. Section 2 is devoted to a short review of the global least squares( GL-LSQR) method. In section 3, we present a new method, namely 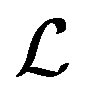 -GL-LSQR, to solve the multiple linear systems (1). we also show how to reduce the low-rank approximate solutions to linear operator
-GL-LSQR, to solve the multiple linear systems (1). we also show how to reduce the low-rank approximate solutions to linear operator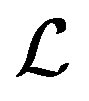 . The section 4 is devoted to some numerical experiments and comparing the new method with the well known LSQR method , when it is applied to s linear systems independently. Finally, we make some concluding remarks in section 5.
. The section 4 is devoted to some numerical experiments and comparing the new method with the well known LSQR method , when it is applied to s linear systems independently. Finally, we make some concluding remarks in section 5.
We use the following notations. For X and Y two matrices in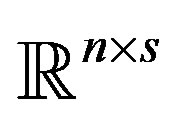 , we consider the following inner product
, we consider the following inner product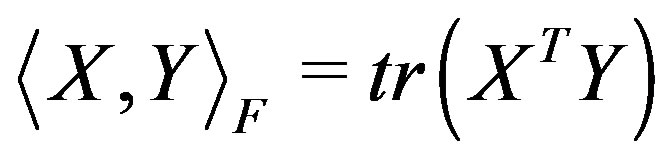 , where
, where 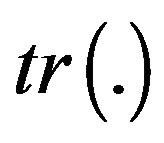 denotes the trace of a matrix. The associated norm is the Frobenious norm denoted by
denotes the trace of a matrix. The associated norm is the Frobenious norm denoted by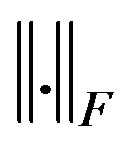 . The notation
. The notation 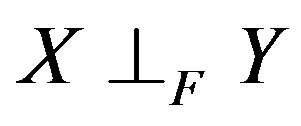 means that
means that 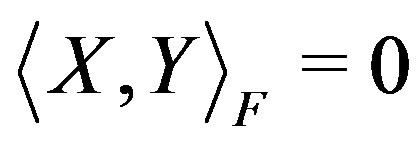 and
and 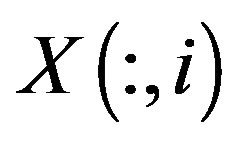 means that the
means that the 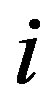 th column of X. Finally, we use the notation * for the following product:
th column of X. Finally, we use the notation * for the following product:
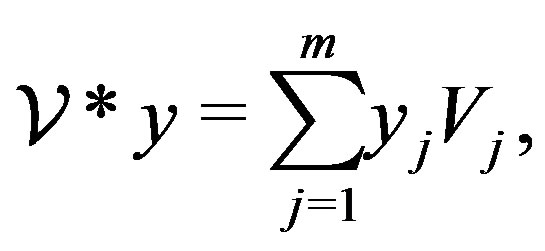 (3)
(3)
where 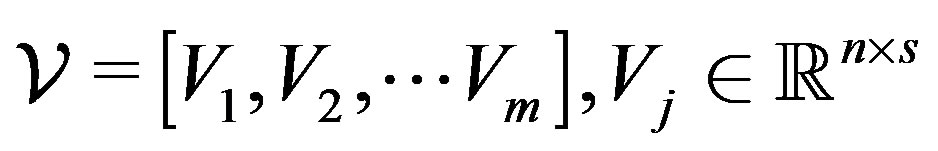 for
for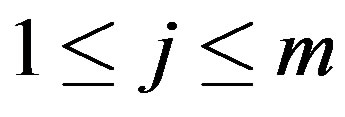 , and
, and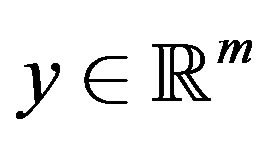 .
.
By the same way, we define
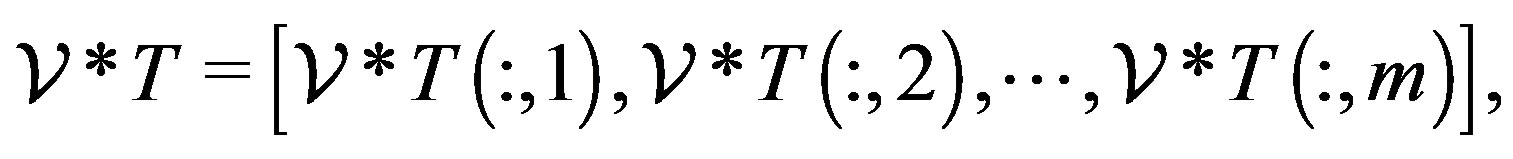 (4)
(4)
where T is the 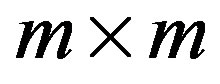 matrix. It is easy to show that the following relations are satisfied:
matrix. It is easy to show that the following relations are satisfied:
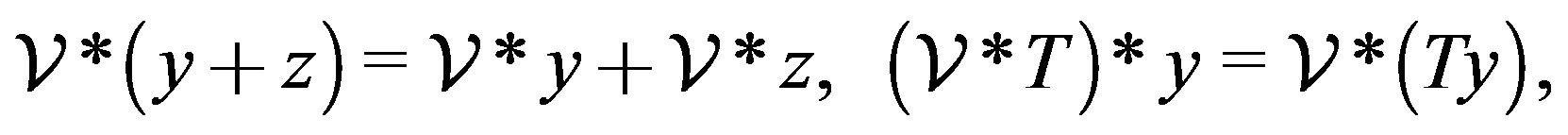 (5)
(5)
where y and z are two vectors of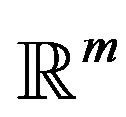 .
.
2. The Global Least Squares (GL-LSQR) Method
In htis section, we recall some fundamental properties of GL-LSQR algorithm [13], which is an iterative method for solving the multiple linear systems (2). When all the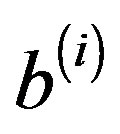 ’s are available simultaneously, the multiple linear systems (2) can be written as
’s are available simultaneously, the multiple linear systems (2) can be written as
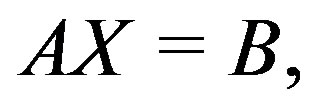 (6)
(6)
where A is an 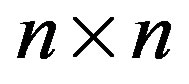 nonsingular arbitrary matrix, B and X are an
nonsingular arbitrary matrix, B and X are an 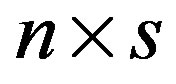 rectangular matrices whose columns are
rectangular matrices whose columns are 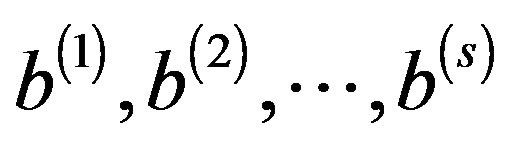 and
and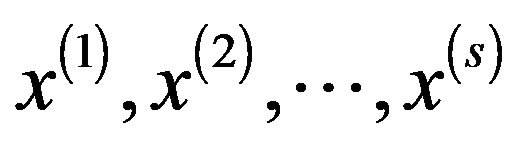 , respectively.
, respectively.
For solving the matrix Equation (6), the GL-LSQR method uses a procedure, namely Global-Bidiag procedure, to reduce A to the global lower bidiagonal form. The Global-Bidiag procedure can be described as follows.
Global-Bidiag (starting matrix B; reduction to global lower bidiagonal form):
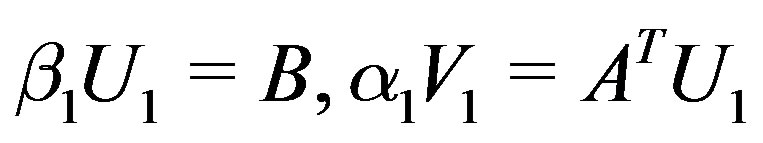
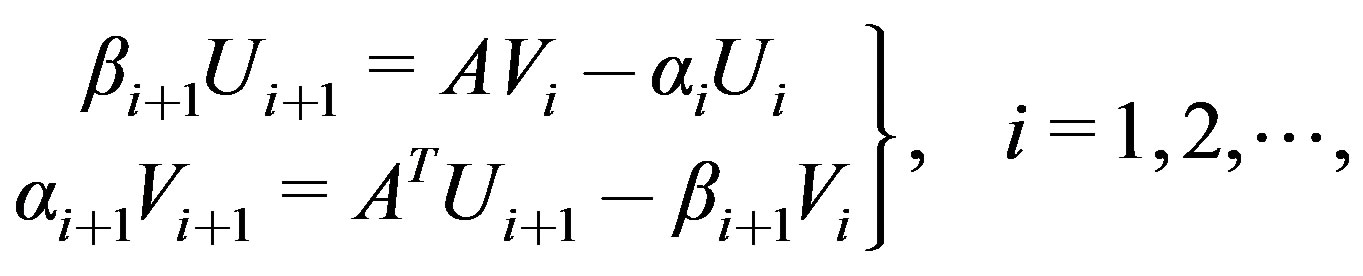 (7)
(7)
where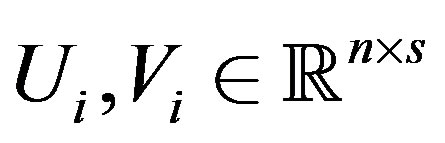 . The scalars
. The scalars 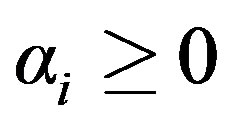 and
and 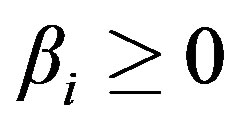 are chosen so that
are chosen so that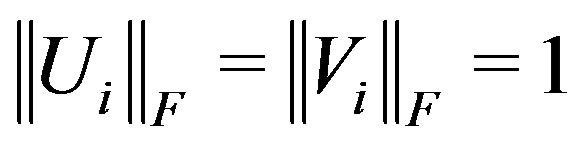 .
.
With the definitions
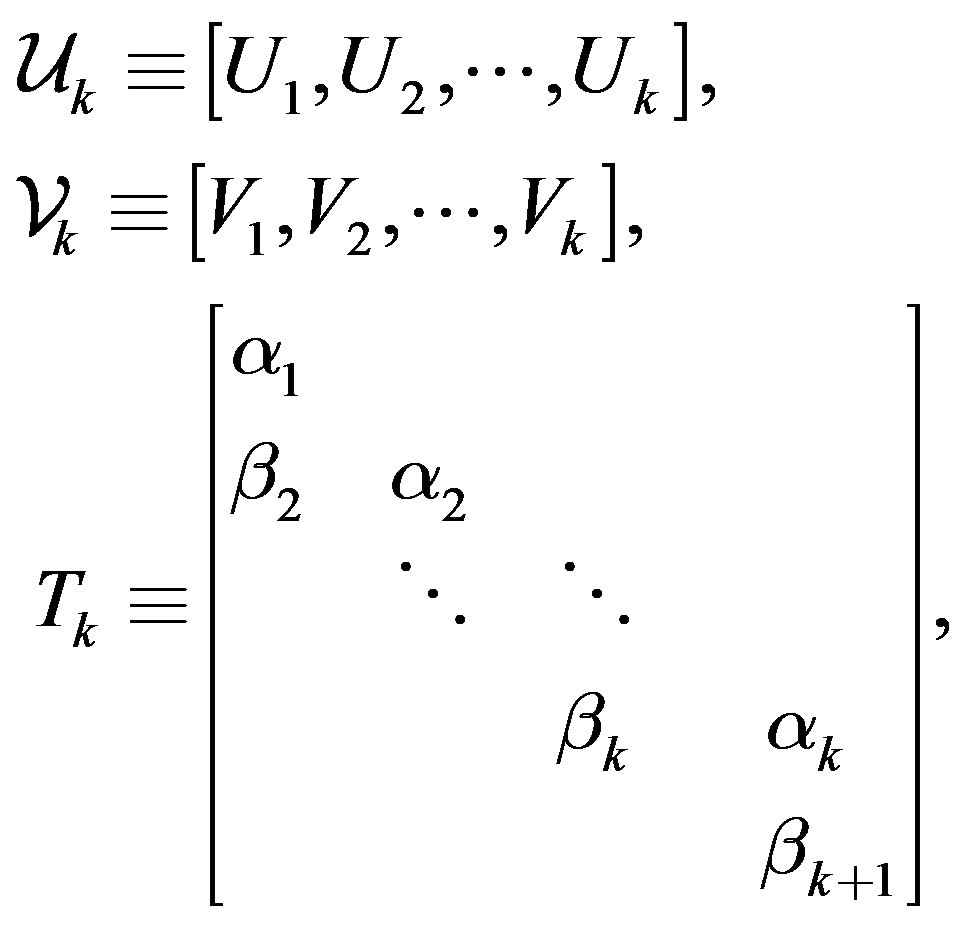
the recurrence relations (7) may be rewritten as:
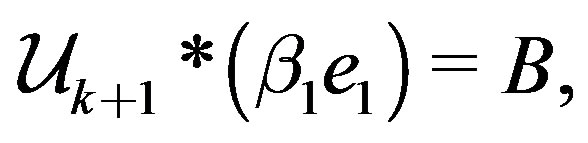 (8)
(8)
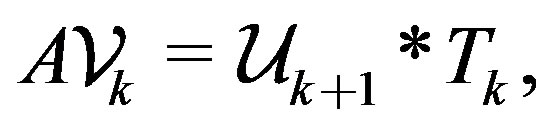 (9)
(9)
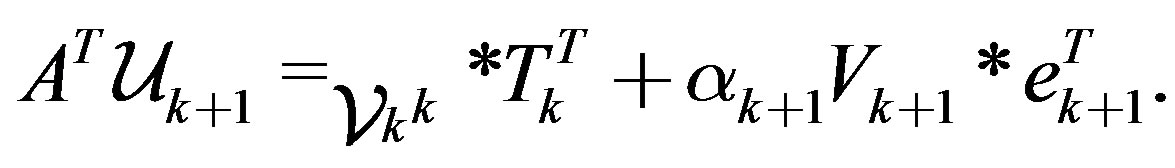 (10)
(10)
For the Global-Bidiag procedure, we have the following propositions.
Proposition 1 [13]. Suppose that k step of the GlobalBidiag procedure have been taken, then the 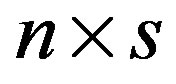 block vectors
block vectors 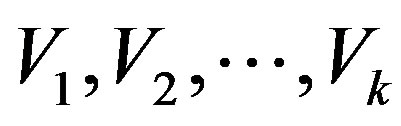 and
and 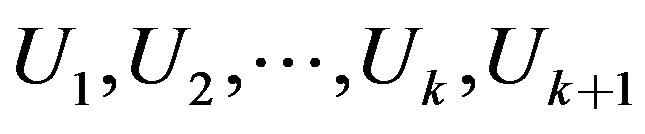 are Forthonormal basis of the Krylov subspaces
are Forthonormal basis of the Krylov subspaces 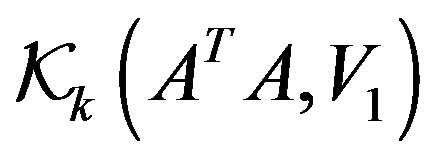 and
and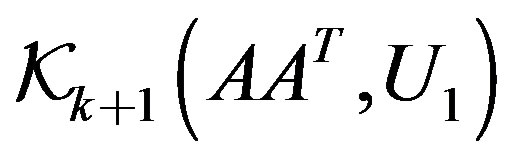 , respectively.
, respectively.
Proposition 2 [13]. The Global-Bidiag procedure will be stopped at step m if and only if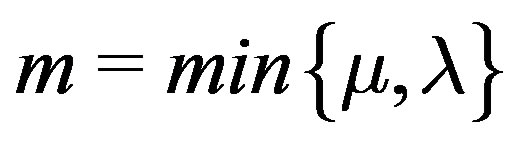 , where
, where 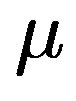 and
and  are the grades of
are the grades of 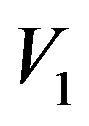 and
and 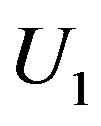 with respect to
with respect to 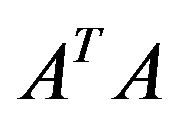 and
and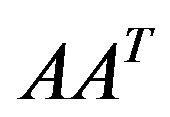 , respectively.
, respectively.
Proposition 3 [13]. Let 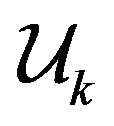 be the matrix defined by
be the matrix defined by 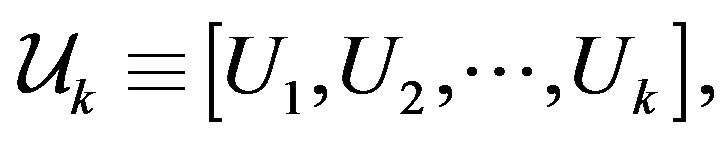 where the
where the 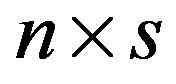 matrices
matrices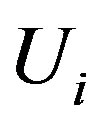 ,
, 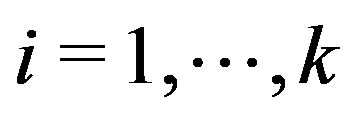 , are generated by the Global-Bidiag procedure. Then
, are generated by the Global-Bidiag procedure. Then
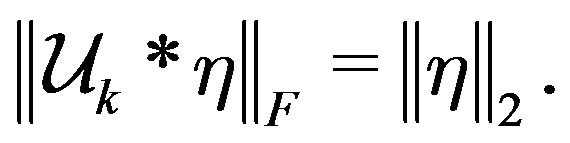
By using the Global-Bidiag procedure, the GL-LSQR algorithm constructs an approximate solution of the form
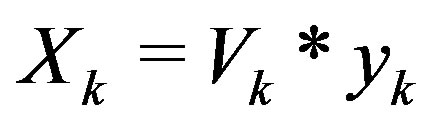 , where
, where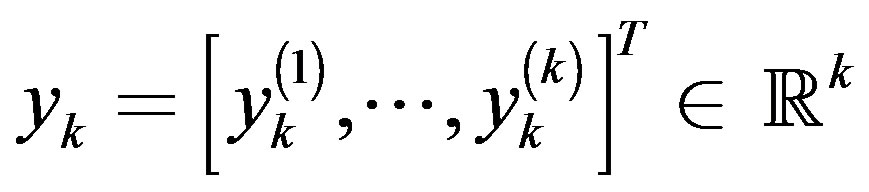 , which solves the least-squares problem,
, which solves the least-squares problem,
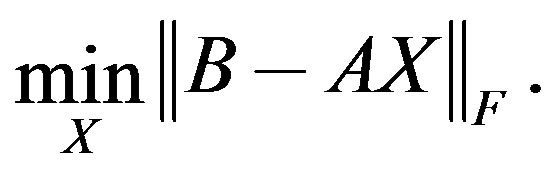
The main steps of the GL-LSQR algorithm can be summarized as follows.
Algorithm 1: Gl-LSQR algorithm
1) Set 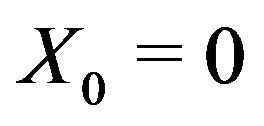
2)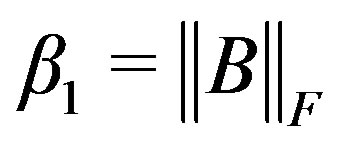 ,
, 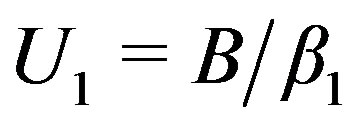 ,
, 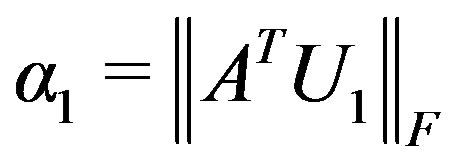 ,
, 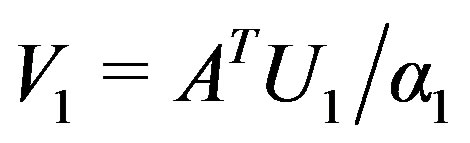 .
.
3) Set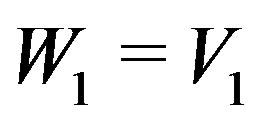 ,
, 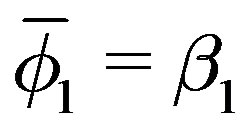 ,
, 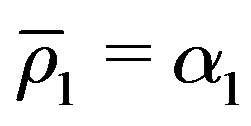
4) For 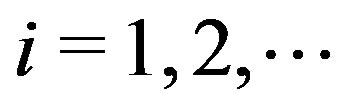 until convergence, Do:
until convergence, Do:
5) 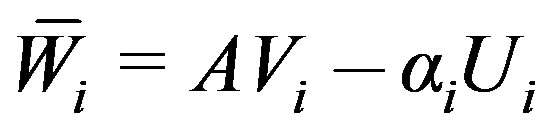
6) 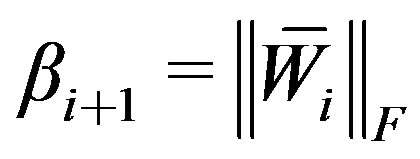
7) 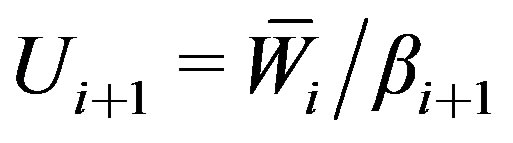
8) 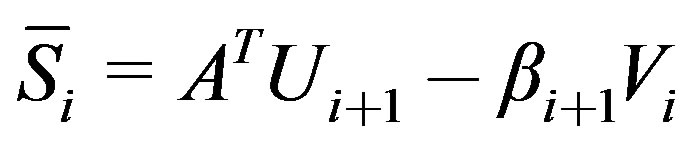
9) 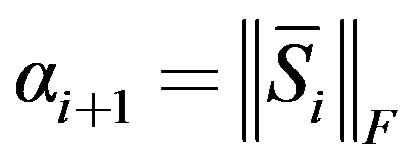
10) 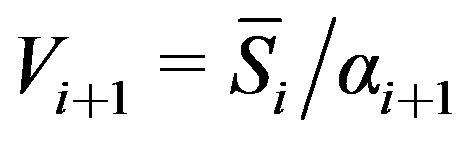
11) 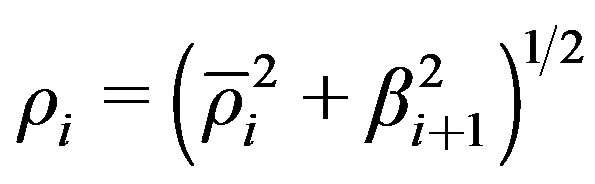
12) 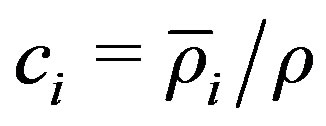
13) 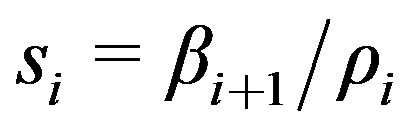
14) 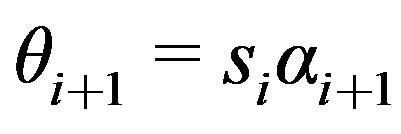
15) 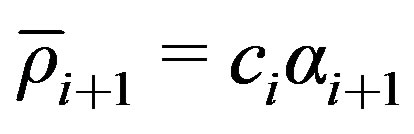
16) 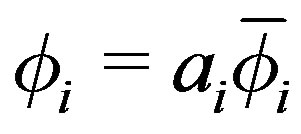
17) 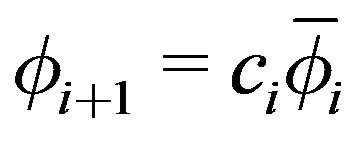
18) 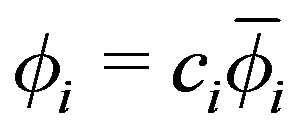
19) 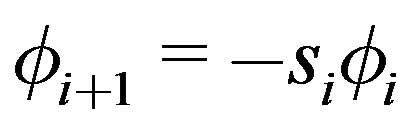
20) 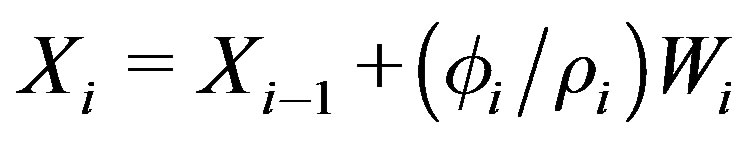
21) 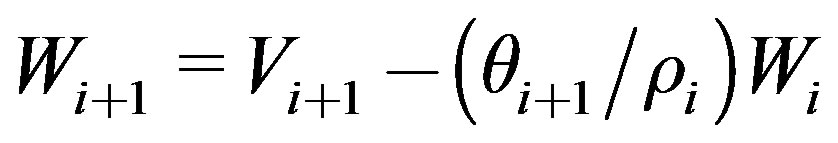
22) If 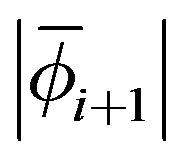 is small enough then stop 23) EndDo.
is small enough then stop 23) EndDo.
More details about the GL-LSQR algorithm can be found [13].
3. The GL-LSQR-Like Operator Method
In this section, we propose a new method for solving the linear systems (1). For this mean, we define the following linear operator
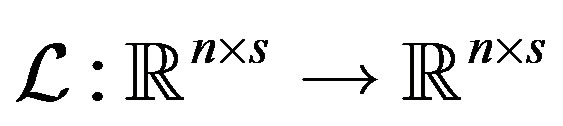 (11)
(11)
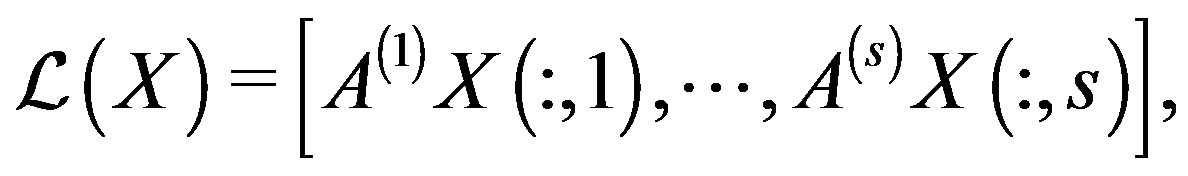 (12)
(12)
where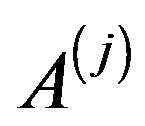 ,
, 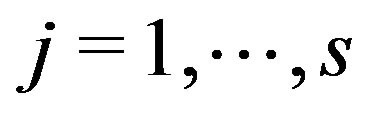 are the coefficient matrices of the multiple linear systems (1). Therefore, the linear systems (1) is written as:
are the coefficient matrices of the multiple linear systems (1). Therefore, the linear systems (1) is written as:
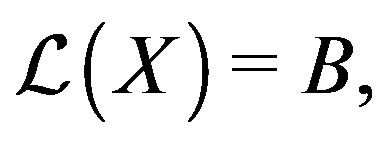 (13)
(13)
where B is an 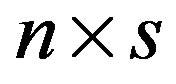 rectangular matrix whose columns are
rectangular matrix whose columns are 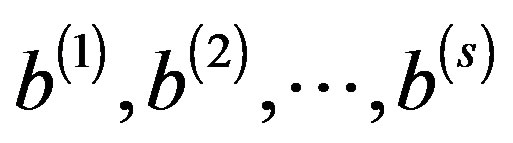 the right hand sides of the linear systems (1).
the right hand sides of the linear systems (1).
Definition 1: Let 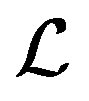 be linear operator (11). Then
be linear operator (11). Then
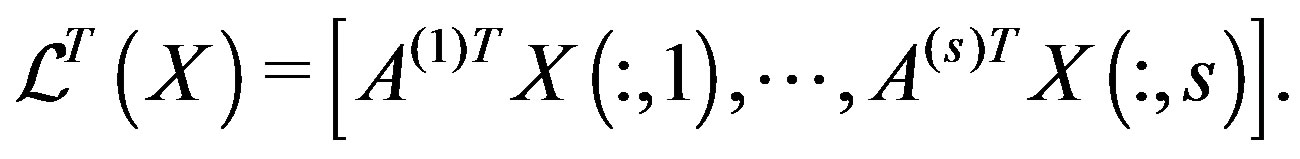
Consider the block operator (13), similar to the wellknown block Krylov subspace
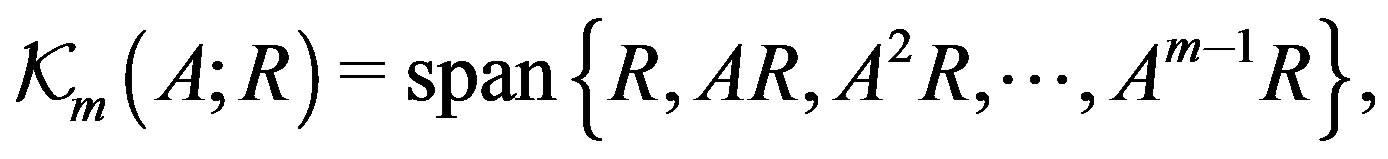
where R is the residual of the operator equation (13), we define the following block Krylov-like subspace.
Definition 2: Let 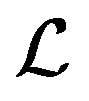 be linear operator (11). Then
be linear operator (11). Then
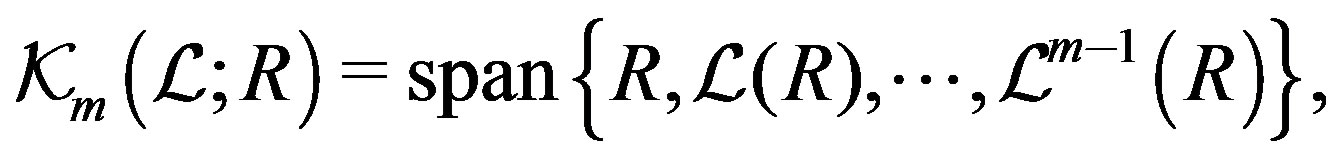
where  and
and  is the combination of two operators.
is the combination of two operators.
Definition 3: Let 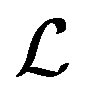 be linear operator (11) and
be linear operator (11) and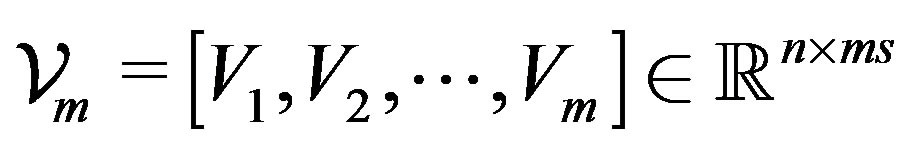 . Then
. Then
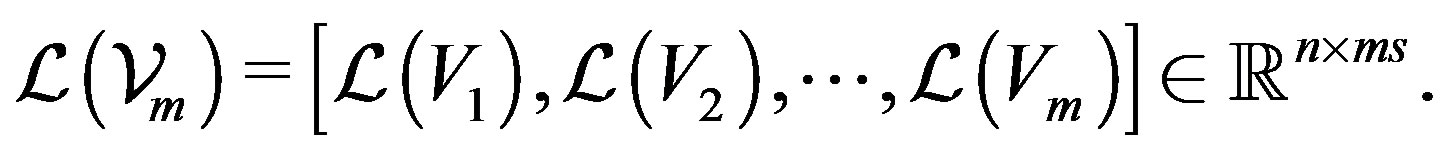
where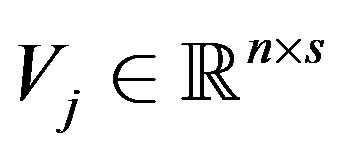 ,
, 
To approximate the solution of the block operator Equation (13), we present a new algorithm, will be referred to 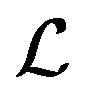 -GL-LSQR algorithm, which is based on the Global-Bidiag-like procedure, will be referred to
-GL-LSQR algorithm, which is based on the Global-Bidiag-like procedure, will be referred to 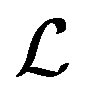 - Bidiag. The
- Bidiag. The 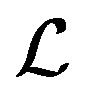 -Bidig procedure reduces the linear operator
-Bidig procedure reduces the linear operator 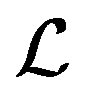 to the lower bidiagonal matrix form. This procedure can be described as follows.
to the lower bidiagonal matrix form. This procedure can be described as follows.
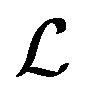 -Bidiag (starting matrix B; reduction to lower bidiagonal matrix form):
-Bidiag (starting matrix B; reduction to lower bidiagonal matrix form):
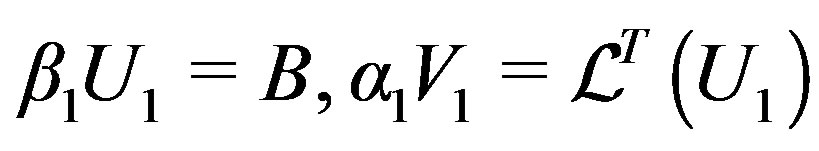
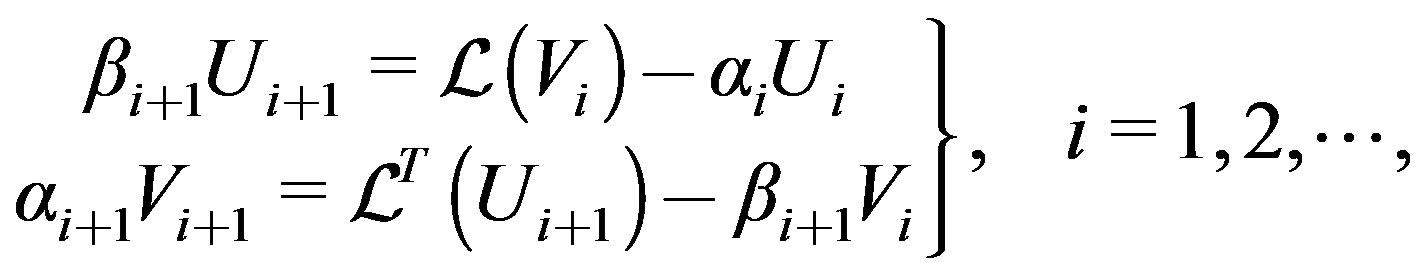 (14)
(14)
where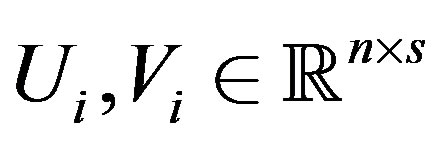 . The scalars
. The scalars 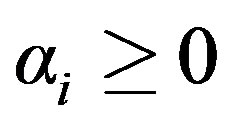 and
and 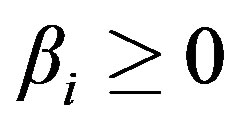 are chosen so that
are chosen so that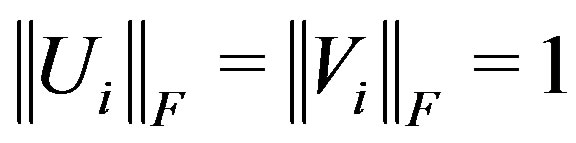 .
.
Similar to Global-Bidiag procedure, we define
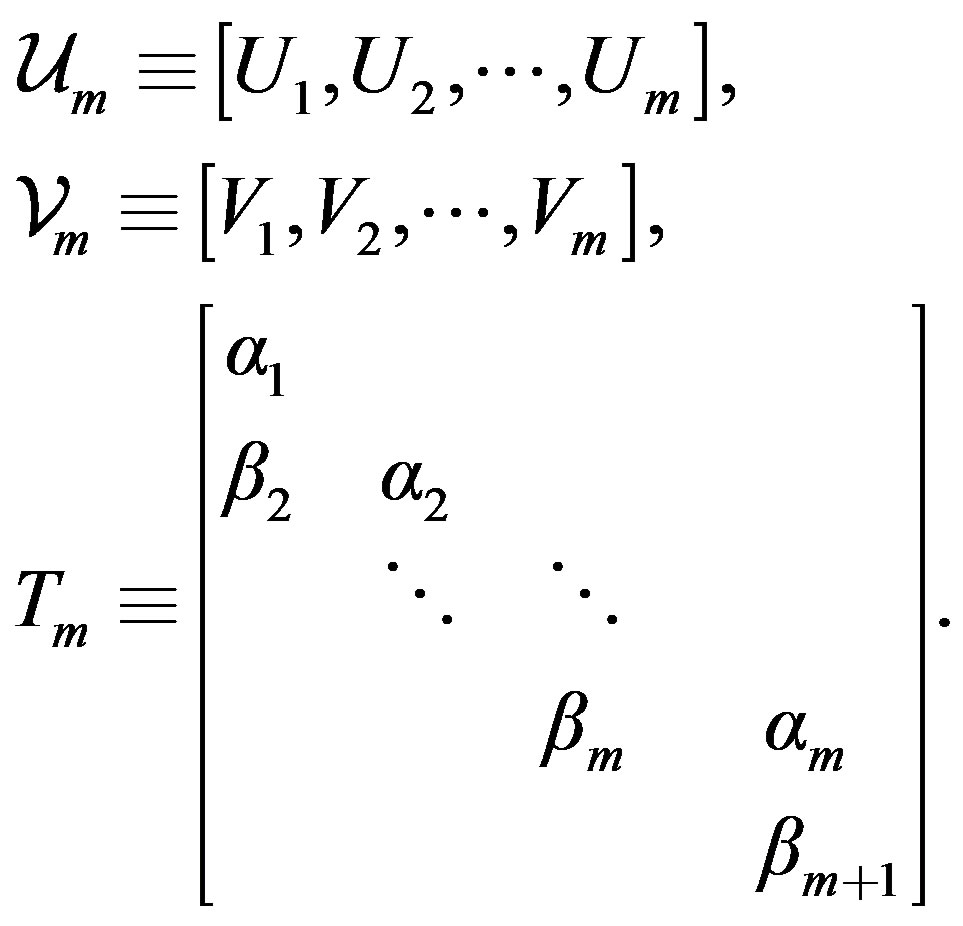
According to notation * and by using the definition 3, the recurrence relations (14) may be rewritten as:
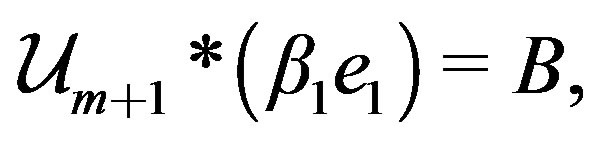 (15)
(15)
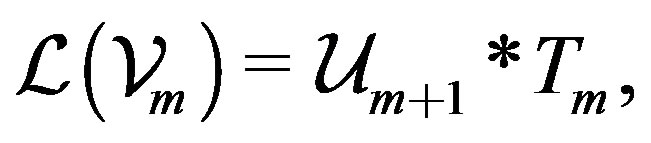 (16)
(16)
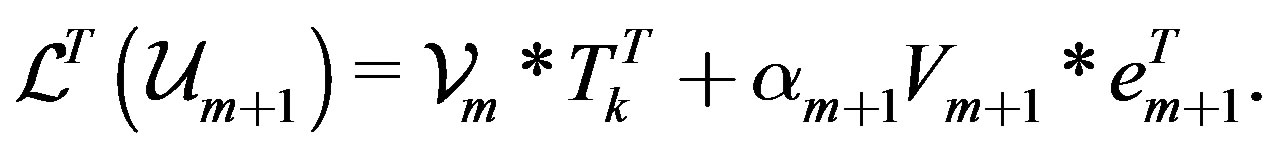 (17)
(17)
Proposition 4. Suppose that k step of the 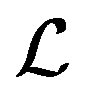 -Bidiag procedure have been taken, then the block vectors
-Bidiag procedure have been taken, then the block vectors  and
and 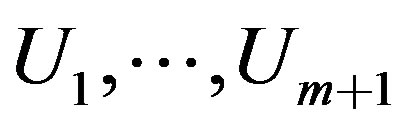 are F-orthonormal basis of the Krylov-like subspace
are F-orthonormal basis of the Krylov-like subspace 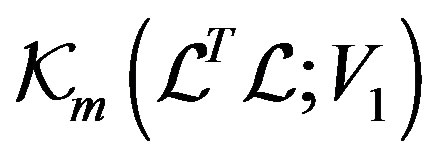 and
and 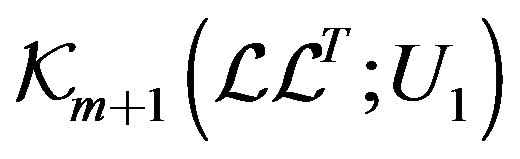 , respectively.
, respectively.
The proof of this proposition is similar to that given in [13].
The quantities generated from the linear operator 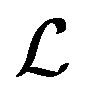 and B by the
and B by the 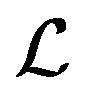 -Bidiag process will now be used to solve the block least squares problem,
-Bidiag process will now be used to solve the block least squares problem,
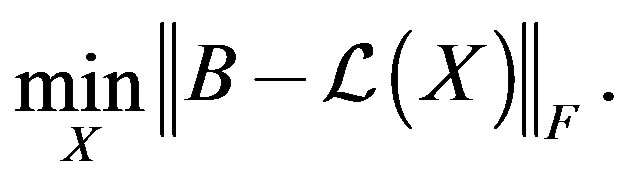
Let the quantities
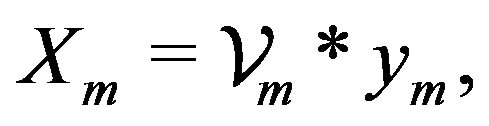 (18)
(18)
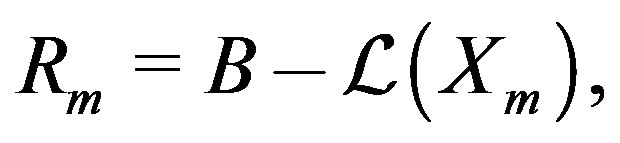 (19)
(19)
be defined, where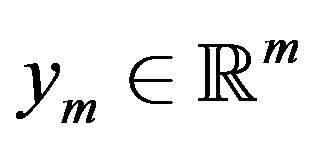 . According to linearity of the operator, it is easy to show that
. According to linearity of the operator, it is easy to show that
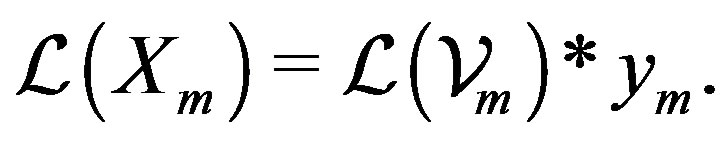
Also it readily follows from (15), (16) and properties of product * the equation
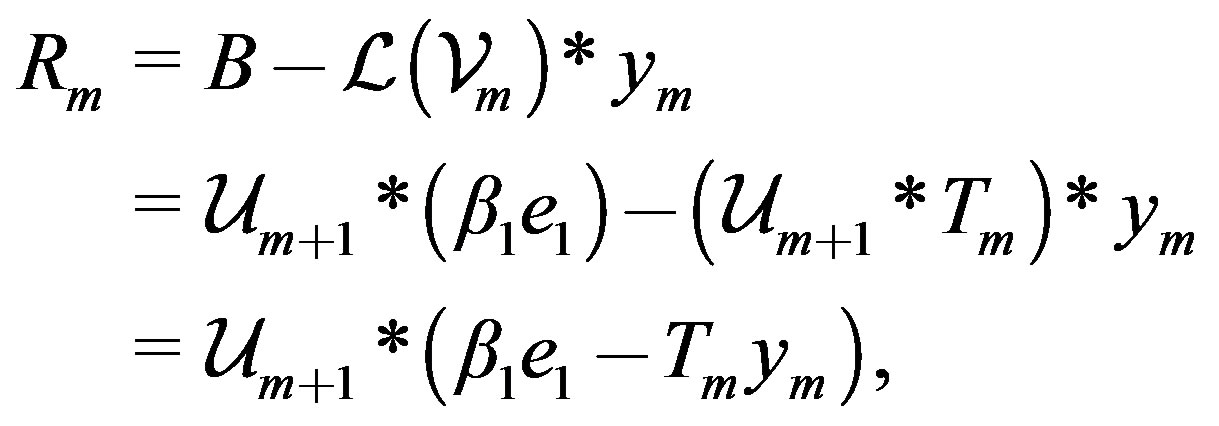
holds to working accuracy.
To minimize the mth residual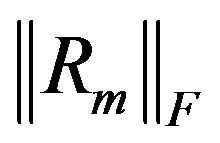 , since
, since 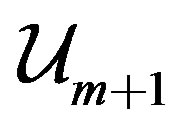 is F-orthonormal and by using the proposition 3, we choose
is F-orthonormal and by using the proposition 3, we choose 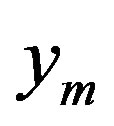 so that
so that
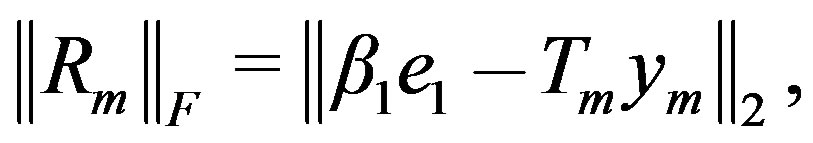 (20)
(20)
is minimum. This minimization problem is carried out by applying the QR decomposition [13], where a unitary matrix 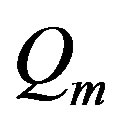 is determined so that
is determined so that

where 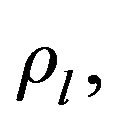
 and
and 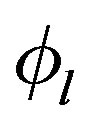 are scalars. The above
are scalars. The above  factorization is determined by constructing the
factorization is determined by constructing the 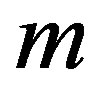 th plane rotation
th plane rotation 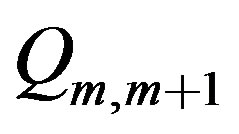 to operate on rows
to operate on rows 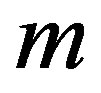 and
and 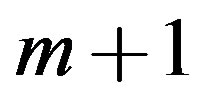 of the transformed
of the transformed 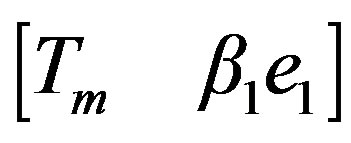 to annihilate
to annihilate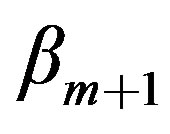 . This gives the following simple recurrence relation:
. This gives the following simple recurrence relation:
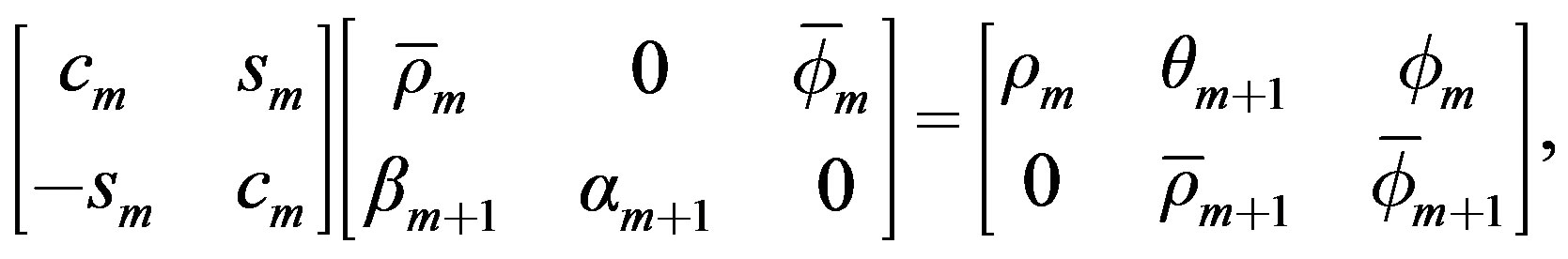
where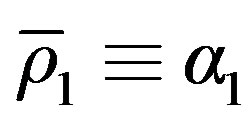 ,
, 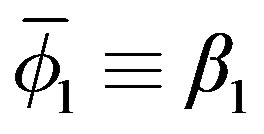 and the scalars
and the scalars 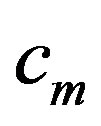 and
and 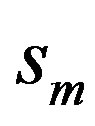 are the nontrivial elements of
are the nontrivial elements of 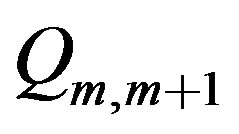 The quantity
The quantity 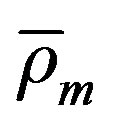 and
and 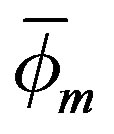 are intermediate scalars that are subsequently replaced by
are intermediate scalars that are subsequently replaced by 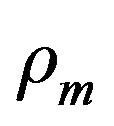 and
and 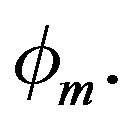
With setting
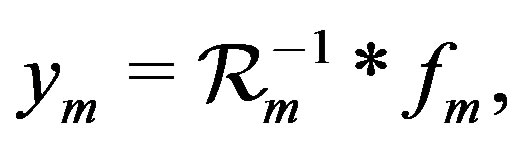
the approximate solution is given by
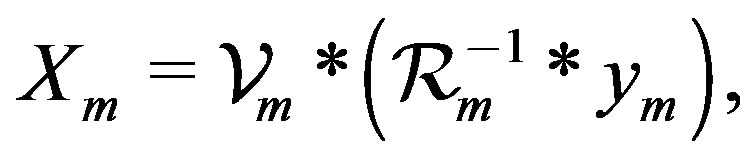 (21)
(21)
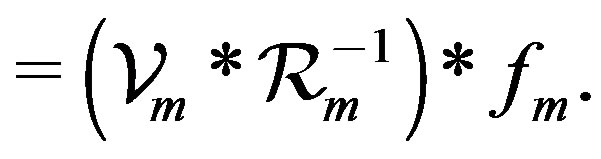 (22)
(22)
Letting
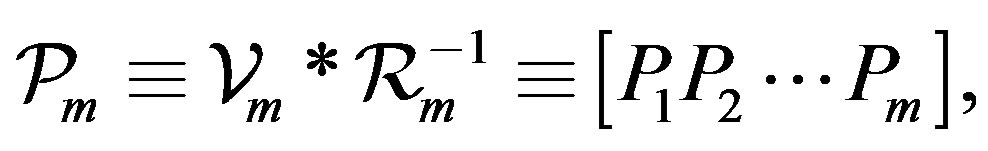
then
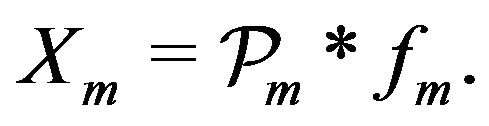
The 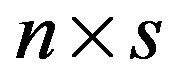 matrix
matrix 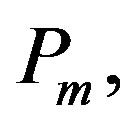 the last block column of
the last block column of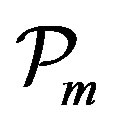 , can be computed from the previous
, can be computed from the previous 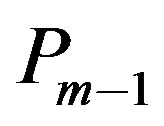 and
and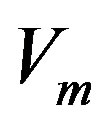 , by the simple update
, by the simple update
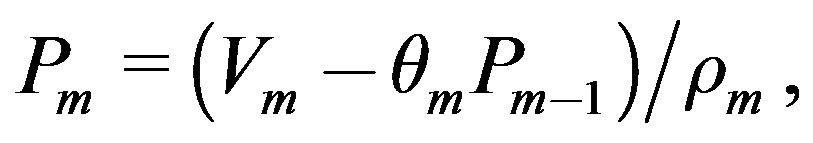 (23)
(23)
also note that,
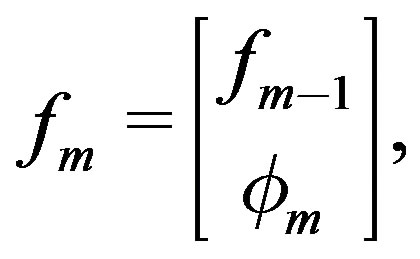
in which
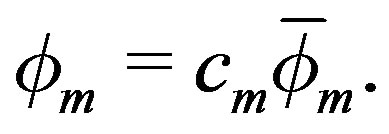
Thus, Xm can be updated at each step, via the relation
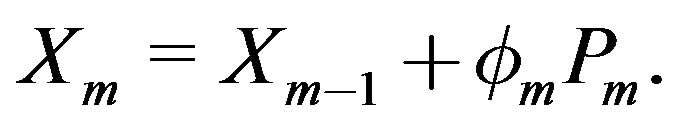
The residual norm 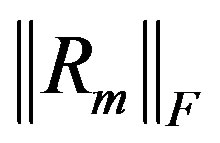 is computed directly from the quantity
is computed directly from the quantity 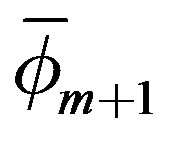 as
as
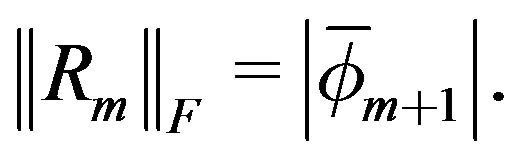
Some of the work in (23) can be eliminated by using matrices 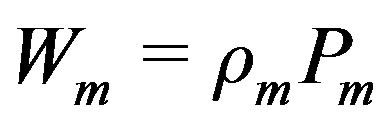 in place of
in place of 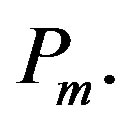 The main steps of the
The main steps of the 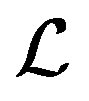 -GL-LSQR algorithm can be summarized as follows.
-GL-LSQR algorithm can be summarized as follows.
Algorithm 2: 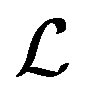 -GL-LSQR algorithm
-GL-LSQR algorithm
1) Set 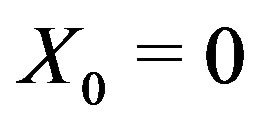
2)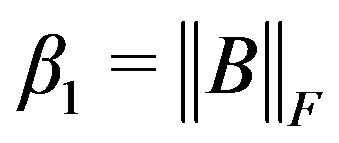 ,
, 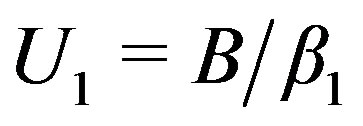 ,
, 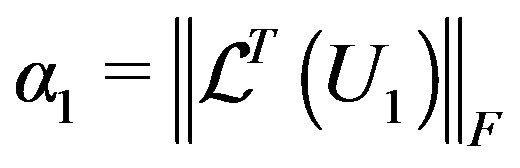 ,
, 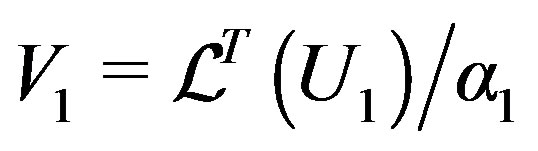 .
.
3) Set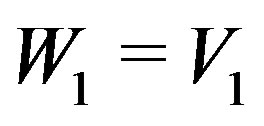 ,
, 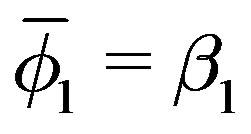 ,
, 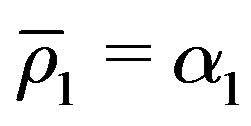
4) For 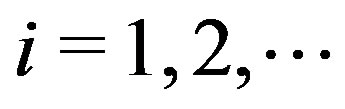 until convergence, Do:
until convergence, Do:
5) 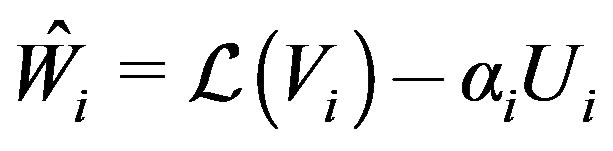
6) 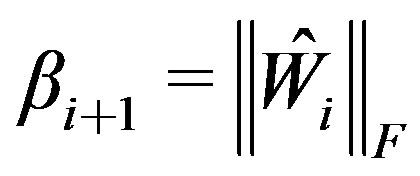
7) 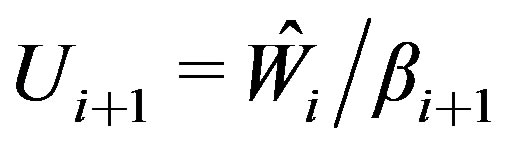
8) 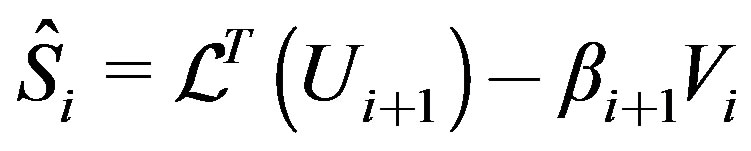
9) 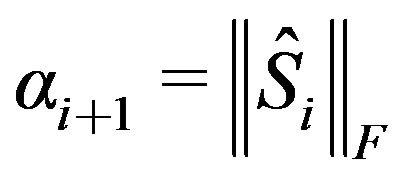
10) 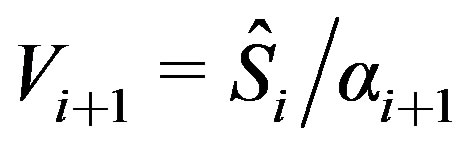
11) 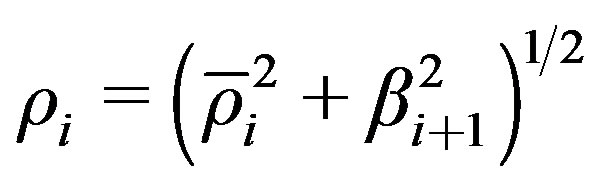
12) 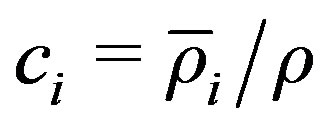
13) 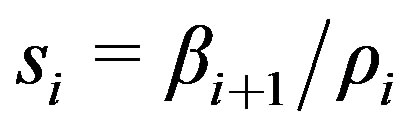
14) 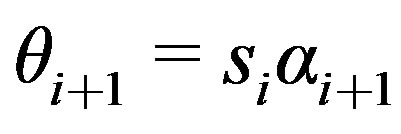
15) 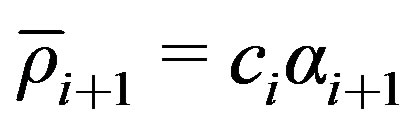
16) 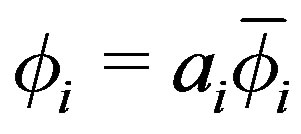
17) 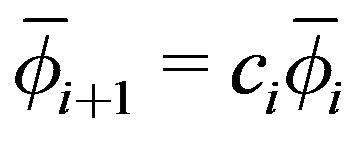
18) 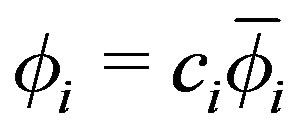
19) 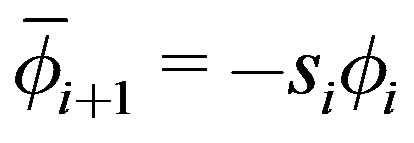
20) 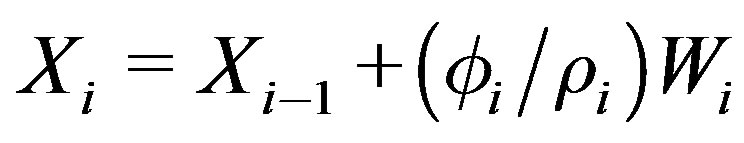
21) 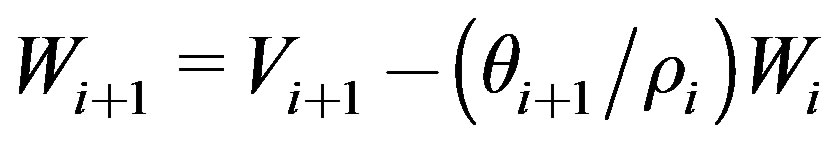
22) If 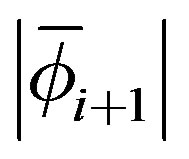 is small enough then stop 23) EndDo.
is small enough then stop 23) EndDo.
As we observe, the 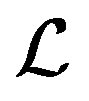 -GL-LSQR algorithm has certain advantages, we obtain simultaneously the approximate solution of the multiple linear systems (1). Also the residual norm is cheaply computed at every stage of the algorithm.
-GL-LSQR algorithm has certain advantages, we obtain simultaneously the approximate solution of the multiple linear systems (1). Also the residual norm is cheaply computed at every stage of the algorithm.
As a application of the new method applying it to solve the Sylvester equation in a special case. Consider the Sylvester equation
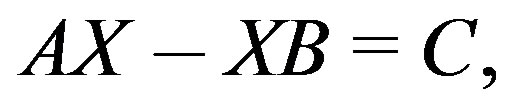
where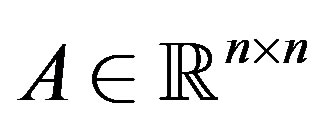 ,
, 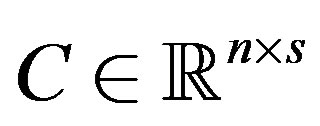 and
and 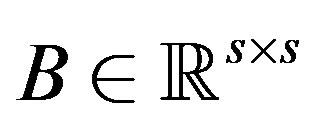 are known and
are known and 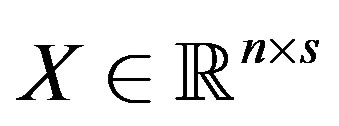 is unknown. By using the Schur decomposition for the symmetric matrix B, the above Sylvester equation is returned to the
is unknown. By using the Schur decomposition for the symmetric matrix B, the above Sylvester equation is returned to the 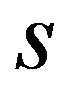 linear systems as follows. There is a unitary matrix Q such that
linear systems as follows. There is a unitary matrix Q such that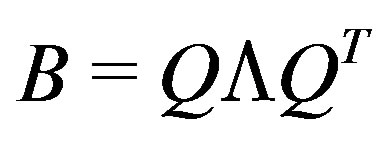 , where
, where  is a diagonal matrix which diagonal elements are the eigenvalues of B. So we have
is a diagonal matrix which diagonal elements are the eigenvalues of B. So we have
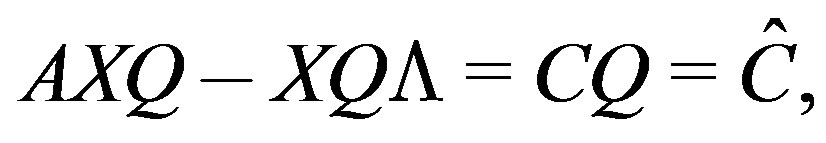
by taking 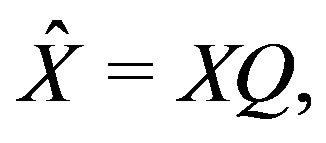 the Sylvester equation is converted to the following s linearsystems
the Sylvester equation is converted to the following s linearsystems
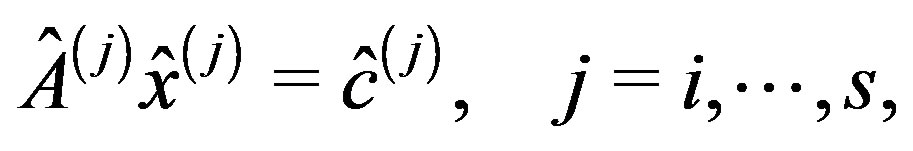
where 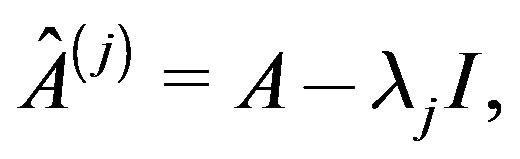
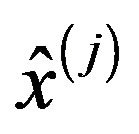 and
and 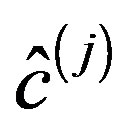 are the j-th colmun of
are the j-th colmun of 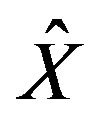 and
and , respectively.
, respectively.
4. Numerical Experiments
In this section, all the numerical experiments were computed in double precision with some MATLAB codes. For all the examples the initial guess 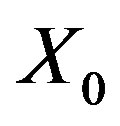 was taken to be zero matrix. We consider two sets of numerical experiments. The first set of numerical experiments contains matrices of the form
was taken to be zero matrix. We consider two sets of numerical experiments. The first set of numerical experiments contains matrices of the form
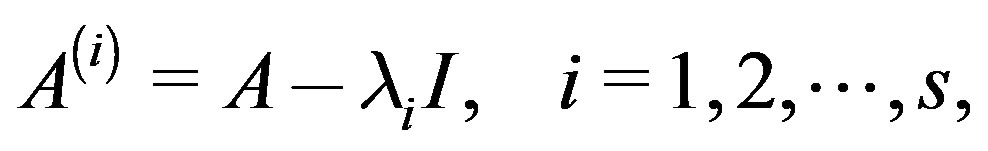
obtained from the Sylvester equation, explained in previous section, where
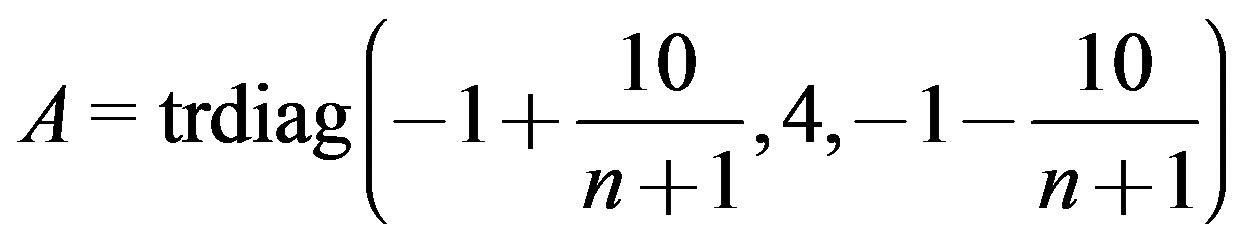 and
and 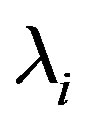 is the eigenvalue of the matrix
is the eigenvalue of the matrix
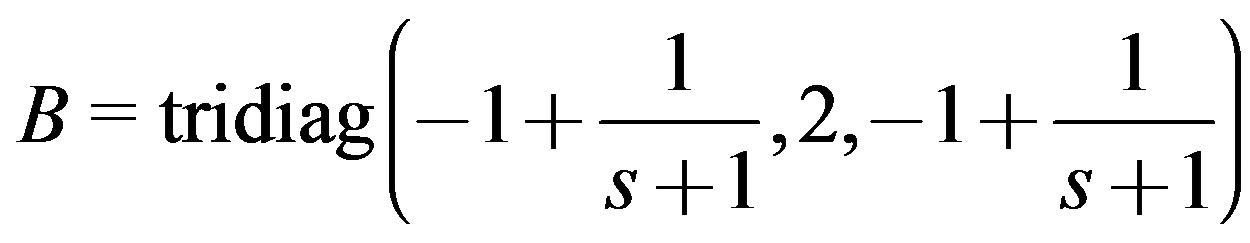 . The right-hand side matrix C is taken
. The right-hand side matrix C is taken 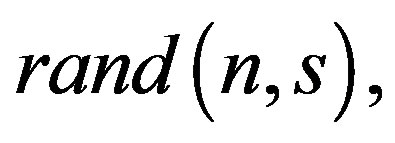 where the function rand creates an
where the function rand creates an 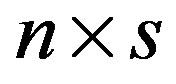 random matrix. The matrices of the second set of experiments arise from the three-point centered discretization of the operator
random matrix. The matrices of the second set of experiments arise from the three-point centered discretization of the operator 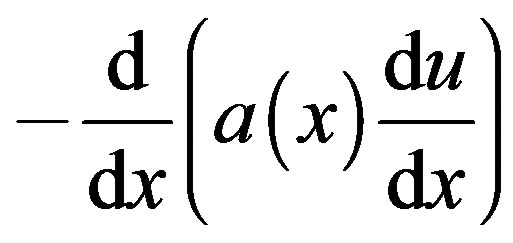
in [0,1] where the function a(x) is given by a(x) = c + dx, where c and d are two parameters. The discretization is performed using a grid size of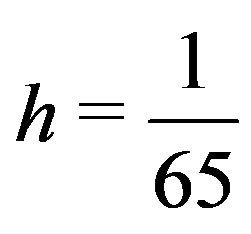 , yielding matrices of size 64 with the values of
, yielding matrices of size 64 with the values of 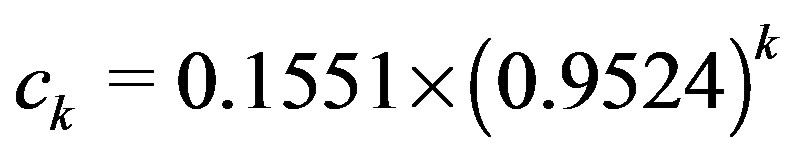 and
and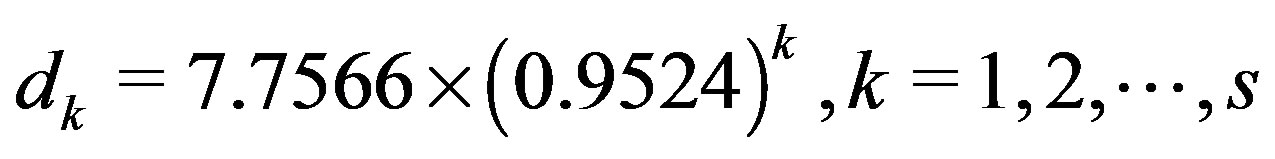 . The righthand sides of these systems are generated randomly with their 2-norms being 1. All the tests were stopped as soon as,
. The righthand sides of these systems are generated randomly with their 2-norms being 1. All the tests were stopped as soon as, 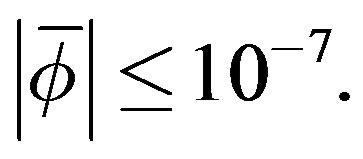
We display the convergence history in Figure 1 and Figure 2 for the systems corresponding to the matrices of the first set of matrices and second set of matrices, respectively. Figure 1 shows that the 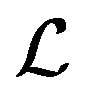 -GL-LSQR algorithm converges, however, Figure 2 shows slowly convergence which can be remedied by using a reliable preconditioner. But we did not deal with the preconditioner techniques in this paper.
-GL-LSQR algorithm converges, however, Figure 2 shows slowly convergence which can be remedied by using a reliable preconditioner. But we did not deal with the preconditioner techniques in this paper.
5. Conclusion
We proposed a new method for solving multiple linear systems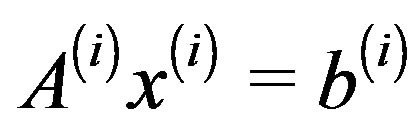 , for
, for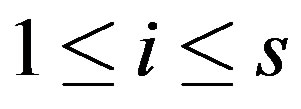 , where the coefficient matrices
, where the coefficient matrices 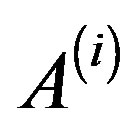 and the right-hand sides
and the right-hand sides 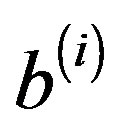 are arbitrary in general. This method has certain advantages which is applied to the arbitrary coefficient matrices
are arbitrary in general. This method has certain advantages which is applied to the arbitrary coefficient matrices 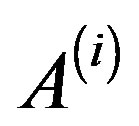 and right-hand sides
and right-hand sides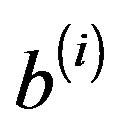 . Also It is not needed to
. Also It is not needed to
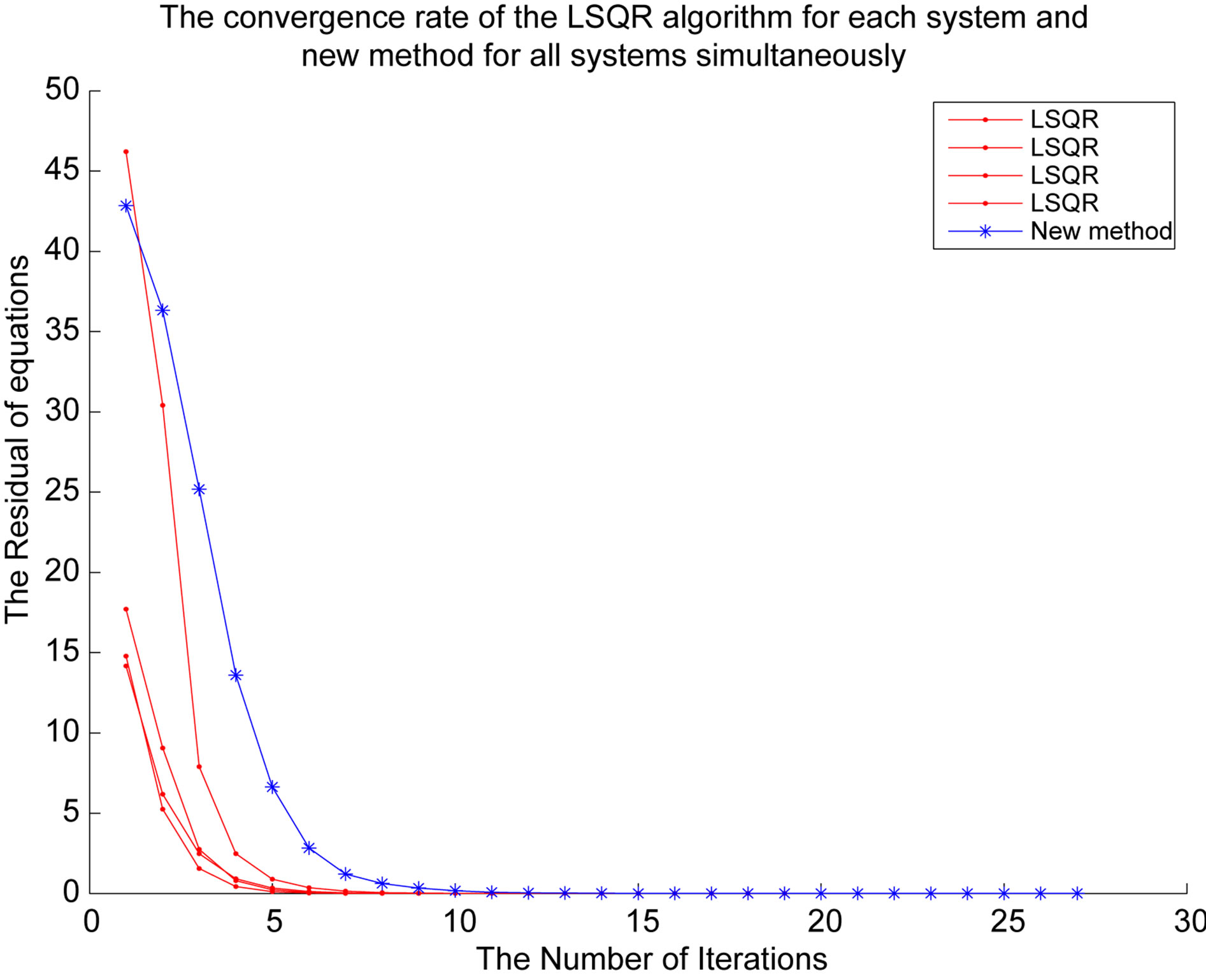
Figure 1. Convergence history of the LSQR algorithm and the new algorithm for the first set matrices with s = 4 and n = 3000.
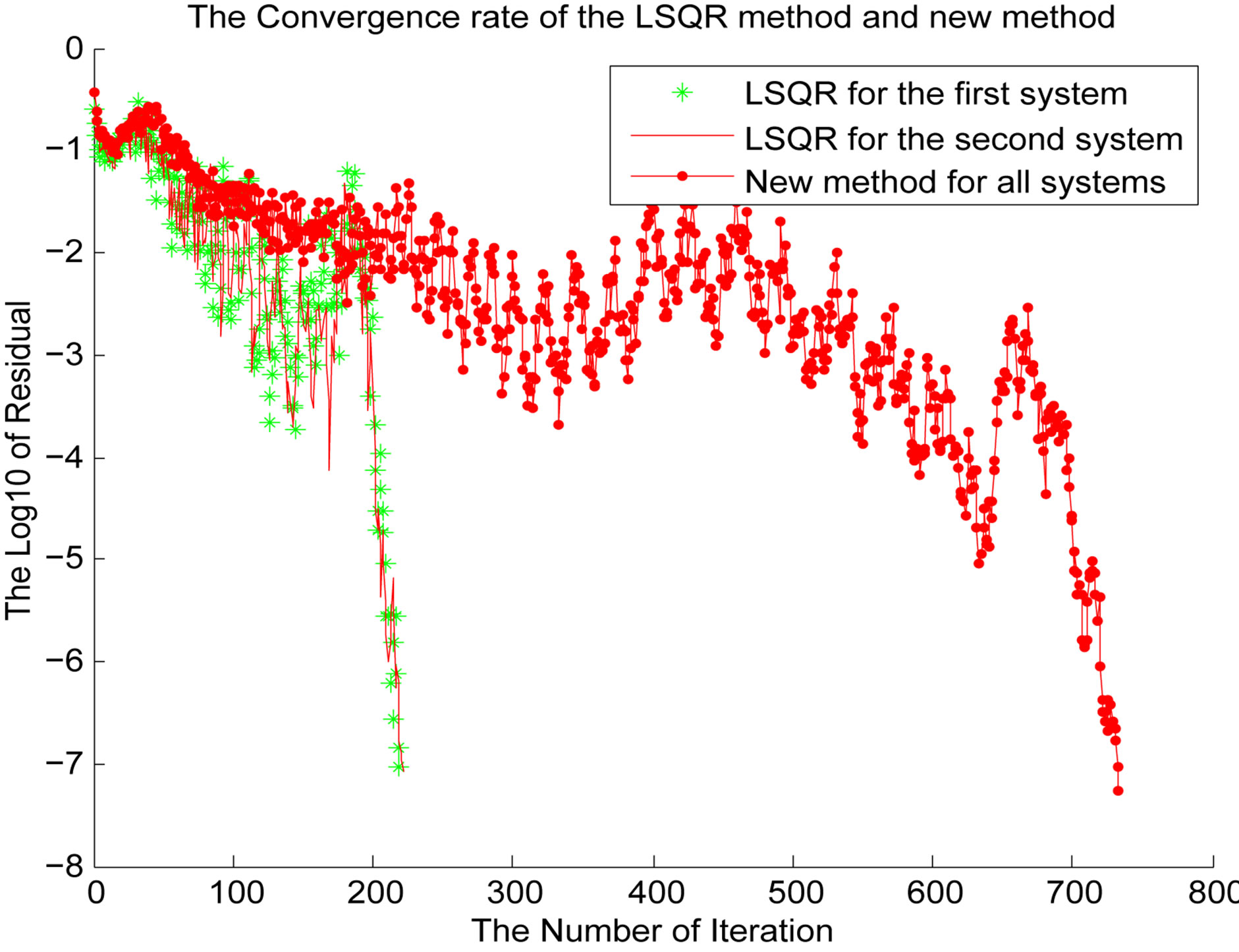
Figure 2. Convergence history of the LSQR algorithm and the new algorithm for the second set matrices with s = 2.
store the basis vectors, it is not needed to predetermine a subspace dimension and the approximate solutions and residuals are cheaply computed at every stage of the algorithm simultaneously because they are updated with short-term recurrence. Applying a reliable preconditioner for the linear systems of Equation (1) may increas the convergence rate, which has not been dicussing in this paper.
6. Acknowledgements
The author would like to thank the anonymous referees for their helpful suggestions, which would greatly inprove the article.
This work is financially supported by the research committee of Persian Gulf University.
REFERENCES
- C. C. Paige and M. A. Saunders, “LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares,” ACM Transactions on Mathematical, Vol. 8, No. 1, 1982, pp. 43-71. doi:10.1145/355984.355989
- R. Plemmons, “FFT-Based RLS in Signal Processing,” Proceeding of the IEEE International Conference on Acoustics, Speech and Signal Processing, Minneapolis, 27-30 April 1993, pp. 571-574.
- W. E. Boyse and A. A. Seidl, “A Block QMR Method for Computing Multiple Simultaneous Solutions to Compex Symmetric Systems,” SIAM Journal on Scientific Computing, Vol. 17, No. 1, 1996, pp. 263-274.
- R. Kress, “Linear Integral Equations,” Springer-Verlag, New York, 1989. doi:10.1007/978-3-642-97146-4
- D. O’Leary, “The Block Conjugate Gradient Algorithm and Related Methods,” Linear Algebra and Its Applications, Vol. 29, 1980, pp. 293-322. doi:10.1016/0024-3795(80)90247-5
- A. Jain, “Fundamentals of Digital Image Processing,” Prentice-Hall, Englewwood Cliffs, 1989.
- S. Karimi and F. Toutounian, “The block Least Squares Method for Solving Nonsymmetric Linear Systems with Multiple Right-Hand Sides,” Applied Mathematics and Computation, Vol. 177, No. 2, 2006, pp. 852-862. doi:10.1016/j.amc.2005.11.038
- G. Golub and C. Loan, “Matrix Computations,” 2nd Edition, Johns Hopkins Press, Bultimore, 1989.
- A. El Guennouni, K. Jbilou and H. Sadok, “The Block Lanczos Method for Linear Systems with Multiple RightHand Sides,” Applied Numerical Mathematics, Vol. 51, No. 2-3, 2004, pp. 243-256.
- A. El Guennouni, K. Jbilou and H. Sadok, “A Block BiCGSTAB Algorithm for Mutiple Linear Systems,” Electronic Transactions on Numerical Analysis, Vol. 16, 2003, pp. 129-142.
- S. Karimi and F. Toutounian, “On the Convergence of the BL-LSQR Algorithm for Solving Matrix Equations,” International Journal of Computer Mathematics, Vol. 88, No. 1, 2011, pp. 171-182. doi:10.1080/00207160903365883
- T. F. Chan and M. K. Ng, “Galerkin Projection Methods for Solving Multiple Linear Systems,” SIAM Journal on Scientific Computing, Vol. 21, No. 3, 2012, pp. 836-850. doi:10.1137/S1064827598310227
- F. Toutounian and S. Karimi, “Global Least Squares (GLLSQR) Method for Solving General Linear Systems with Several Right-Hand Sides,” Applied Mathematics and Computation, Vol. 178, No. 2, 2006, pp. 452-460. doi:10.1016/j.amc.2005.11.065

