Advances in Linear Algebra & Matrix Theory
Vol.2 No.2(2012), Article ID:20470,7 pages DOI:10.4236/alamt.2012.22002
Solving the Class Equation 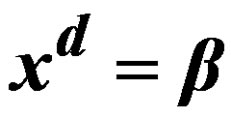 in an Alternating Group for Each
in an Alternating Group for Each 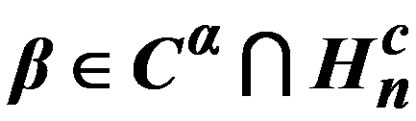 and
and 
1Department of Mathematics, College of Science, University of Basra, Basra, Iraq
2School of Mathematical Sciences, Universiti Sains Malaysia, Penang, Malaysia
Email: shuker.alsalem@gmail.com, andy@cs.usm.my
Received March 6, 2012; revised April 1, 2012; accepted May 1, 2012
Keywords: Alternating Groups; Permutations; Conjugate Classes; Cycle Type; Frobenius Equation
ABSTRACT
The main purpose of this paper is to solve the class equation 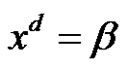 in an alternating group, (i.e. find the solutions set
in an alternating group, (i.e. find the solutions set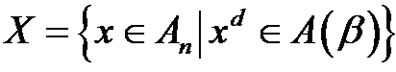 ) and find the number of these solutions
) and find the number of these solutions 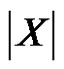 where
where 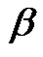 ranges over the conjugacy class
ranges over the conjugacy class 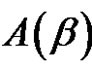 in
in 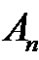 and d is a positive integer. In this paper we solve the class equation
and d is a positive integer. In this paper we solve the class equation 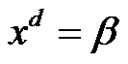 in
in 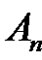 where
where , for all
, for all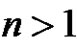 .
. 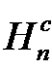 is the complement set of
is the complement set of 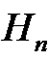 where
where  {
{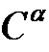 of
of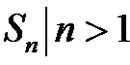 , with all parts
, with all parts 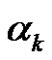 of
of 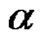 are different and odd}.
are different and odd}. 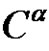 is conjugacy class of
is conjugacy class of 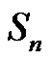 and form class
and form class 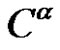 depends on the cycle type
depends on the cycle type 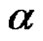 of its elements If
of its elements If 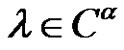 and
and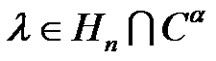 , then
, then 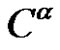 splits into the two classes
splits into the two classes 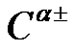 of
of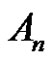 .
.
1. Introduction
The Frobenius equation 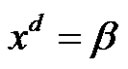 in finite groups was introduced by G. Frobenius and then was studied by many others such as ([1-4]). Where they dealt with some types of finite groups like finite cyclic groups, finite pgroups, Wreath products of finite groups, etc. Choose any
in finite groups was introduced by G. Frobenius and then was studied by many others such as ([1-4]). Where they dealt with some types of finite groups like finite cyclic groups, finite pgroups, Wreath products of finite groups, etc. Choose any 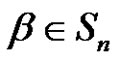 and write it as
and write it as . With
. With 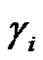 disjoint cycles of length
disjoint cycles of length 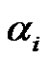 and
and  is the number of disjoint cycle factors including the 1-cycle of
is the number of disjoint cycle factors including the 1-cycle of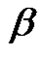 . Since disjoint cycles commute, we can assume that
. Since disjoint cycles commute, we can assume that
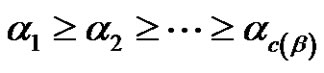 . Therefore
. Therefore  is a partition of n and it is call cycle type of
is a partition of n and it is call cycle type of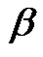 . Let
. Let 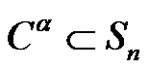 be the set of all elements with cycle type
be the set of all elements with cycle type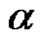 , then we can determine the conjugate class of
, then we can determine the conjugate class of 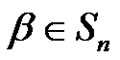 by using cycle type of
by using cycle type of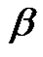 , since each pair of
, since each pair of  and
and 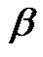 in
in 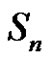 are conjugate if they have the same cycle type (see [5]). Therefore, the number of conjugacy classes of
are conjugate if they have the same cycle type (see [5]). Therefore, the number of conjugacy classes of 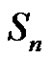 is the number of partitions of n. However, this is not necessarily true in an alternating group. Let
is the number of partitions of n. However, this is not necessarily true in an alternating group. Let  and
and 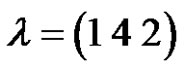 are two permutations in
are two permutations in  we have they are belong to the same conjugate class
we have they are belong to the same conjugate class  in
in  (i.e.
(i.e. ) since
) since
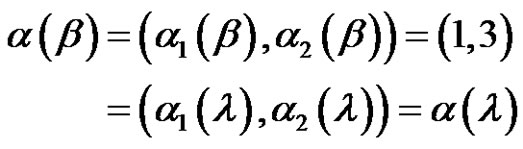
that means they have the same cycle type but in fact 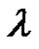 and
and 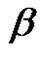 are not conjugate in
are not conjugate in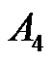 , also let
, also let
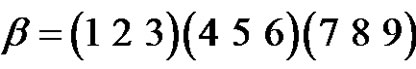 and
and 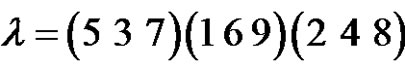 in
in  we have they are belong to the same conjugate class
we have they are belong to the same conjugate class 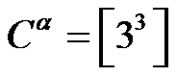 in
in 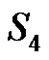 since
since 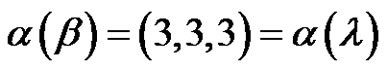
but here they are conjugate in . So from the first and second examples we consider it is not necessarily if two permutations have the same cycle type are conjugate in
. So from the first and second examples we consider it is not necessarily if two permutations have the same cycle type are conjugate in  therefore in this work we discuss in detail the conjugacy classes in an alternating group and we denote to conjugacy class of
therefore in this work we discuss in detail the conjugacy classes in an alternating group and we denote to conjugacy class of 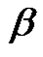 in
in 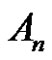 by
by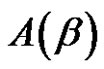 . Also we introduce some theorems to solve the class equation
. Also we introduce some theorems to solve the class equation 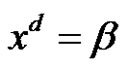 in
in 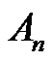 where
where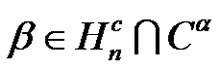 , for all
, for all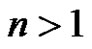 .
.
1.1. Definition [6]
A partition 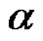 is a sequence of nonnegative integers
is a sequence of nonnegative integers 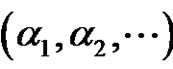 with
with 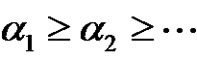 and
and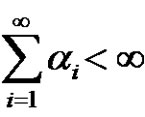 . The length
. The length
 and the size
and the size 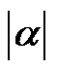 of
of 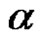 are defined as
are defined as
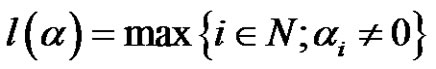
and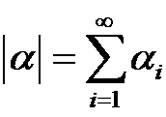 . We set
. We set  for
for . An element of
. An element of  is called a partition of n.
is called a partition of n.
1.2. Remark [6]
We only write the non zero components of a partition. Choose any 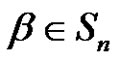 and write it as
and write it as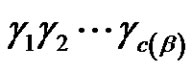 . With
. With 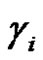 disjoint cycles of length
disjoint cycles of length 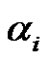 and
and 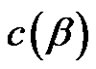 is the number of disjoint cycle factors including the 1-cycle of
is the number of disjoint cycle factors including the 1-cycle of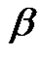 . Since disjoint cycles commute, we can assume that
. Since disjoint cycles commute, we can assume that
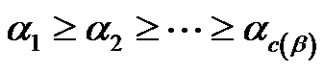 . Therefore
. Therefore 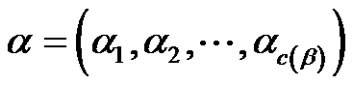 is a partition of n and each
is a partition of n and each 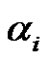 is called part of
is called part of .
.
1.3. Definition [6]
We call the partition

the cycle type of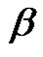 .
.
1.4. Definition [6]
Let 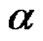 be a partition of n. We define
be a partition of n. We define 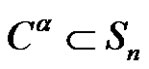 to be the set of all elements with cycle type
to be the set of all elements with cycle type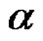 .
.
1.5. Definition [6]
Let 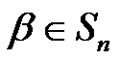 be given. We define
be given. We define 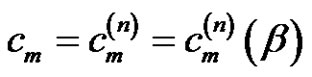 to be the number of cycles of length m of
to be the number of cycles of length m of .
.
1.6. Remarks
1) If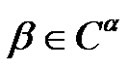 , then we write
, then we write .
.
2) The relationship between partitions and 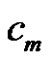 is as follows: if
is as follows: if 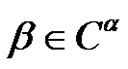 is given then
is given then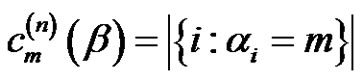 , (see [6])
, (see [6])
3) The cardinality of each 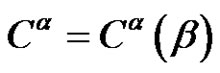 can be found as follows:
can be found as follows: 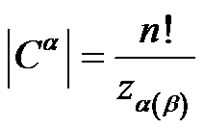 with
with 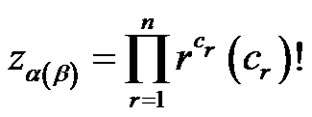 and
and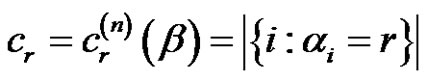 , (see [7]).
, (see [7]).
4) 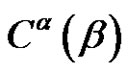 splits into two An-classes of equal order iff
splits into two An-classes of equal order iff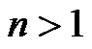 , and the non-zero parts of
, and the non-zero parts of 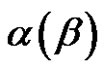 are different and odd, in every other case
are different and odd, in every other case 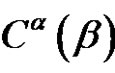 does not split, (see [8]).
does not split, (see [8]).
1.7. Lemma [9]
Let p prime number and 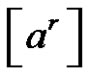 a conjugate class of symmetric group. If p does not divide a, then the solutions of
a conjugate class of symmetric group. If p does not divide a, then the solutions of 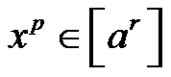 are:
are:
1)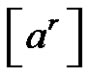 , if
, if 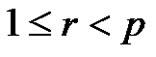
2)  if
if 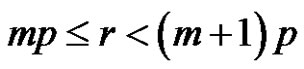
1.8. Lemma [9]
Let p and q be different prime numbers and 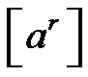 a conjugate class of symmetric group. If
a conjugate class of symmetric group. If 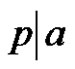 and q does not divide a, then the solutions of
and q does not divide a, then the solutions of 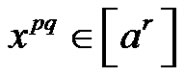 are:
are:
1) , where i and j are solutions of the equation
, where i and j are solutions of the equation 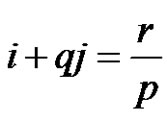 if
if .
.
2) No solution if p does not divide r.
1.9. Lemma [9]
Let p and q be different prime numbers and 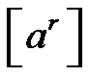 a conjugate class in Sn. If p does not divide a and q does not divide a, then the solutions of
a conjugate class in Sn. If p does not divide a and q does not divide a, then the solutions of  are
are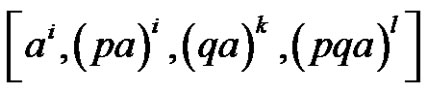 , where i, j, k and l are nonnegative integers and solutions of the equation i + pj + qk + pql = r.
, where i, j, k and l are nonnegative integers and solutions of the equation i + pj + qk + pql = r.
2. Conjugacy Class 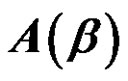 2075 /> of An [10]
2075 /> of An [10]
Let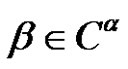 , where
, where 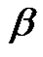 is a permutation in an alternating group. We define the
is a permutation in an alternating group. We define the 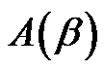 conjugacy class of
conjugacy class of 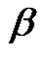 in
in  by:
by:
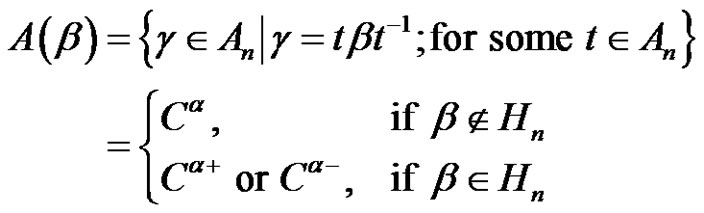
where  {
{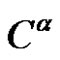 of
of , with all parts
, with all parts 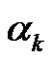 of
of 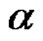 different and odd}.
different and odd}.
2.1. Remarks
1) .
.
2)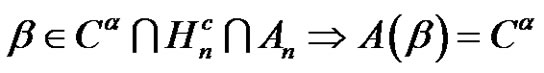 , where
, where 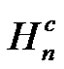 is complement of
is complement of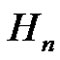 .
.
3) 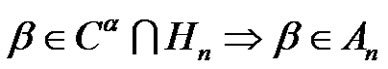 and
and 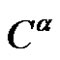 split into two classes
split into two classes 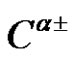 of
of .
.
4) If , and
, and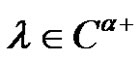 , then
, then
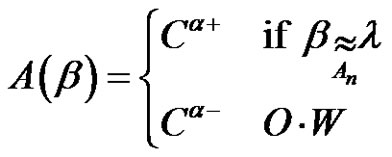
5) If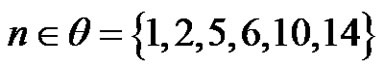 , then for each
, then for each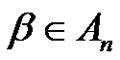 ,
, 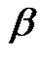 is conjugate to
is conjugate to 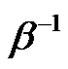 in
in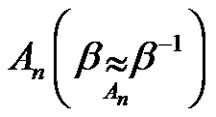 .
.
2.2. Definition
Let  {
{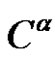 of
of 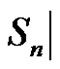 the number of parts
the number of parts 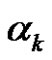 of
of 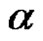 with the property
with the property 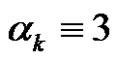 (mod 4) is odd}. Then, for each
(mod 4) is odd}. Then, for each ,
,  of
of  is defined by
is defined by
 ,
,
 .
.
2.3. Definition
Let  {
{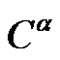 of
of 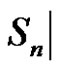 the number of parts
the number of parts 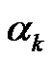 of
of 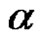 with the property
with the property  (mod 4) is even}. Then, for each
(mod 4) is even}. Then, for each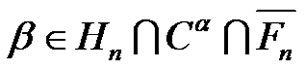 ,
, 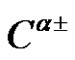 of
of 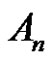 is defined by
is defined by
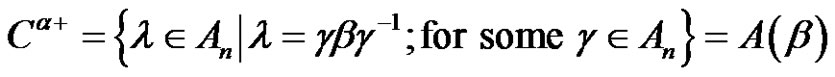 ,
,
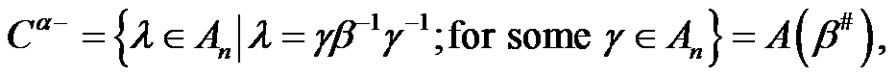
where  does not conjugate to
does not conjugate to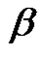 .
.
3. Results for Even Permutations in 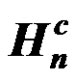
3.1. Theorem
Let 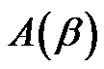 be the conjugacy class of
be the conjugacy class of  in
in . If p is a prime number and does not divide a,
. If p is a prime number and does not divide a, 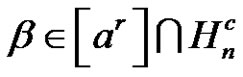 , where
, where  is a class of
is a class of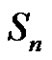 , then the solutions of
, then the solutions of  are
are
1) 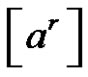 if
if 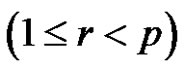 and (a is odd or (a and r) are even)
and (a is odd or (a and r) are even)
2) 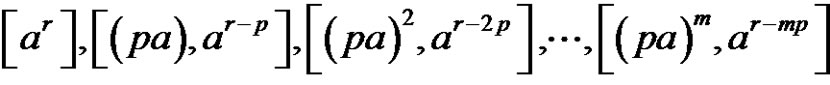 if [((a and p) are odd) or (p is odd and (a and r) are even)] and
if [((a and p) are odd) or (p is odd and (a and r) are even)] and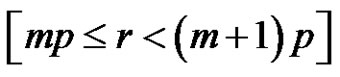
3) 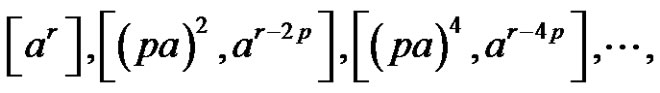

if [(a is odd and p is even) or (a, p and r are even)] and [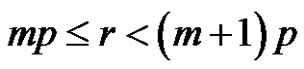 and m is even]
and m is even]
4) 
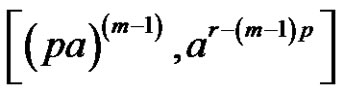
if [(a is odd and p is even) or (a, p and r are even)] and [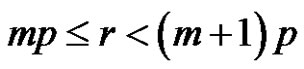 and m is odd]
and m is odd]
5) 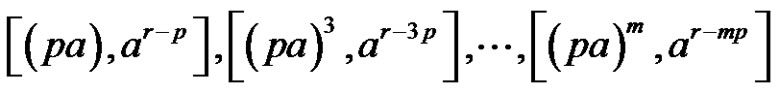 if
if
[(a and p) are even and r is odd] and [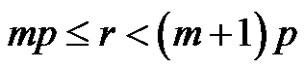 and m is odd]
and m is odd]
6) 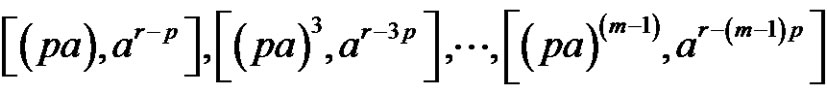
if [(a and p) are even and r is odd)] and [ and m is even], or
and m is even], or
7) Does not exist, if [(a is even and (p and r) are odd].
Proof
Given that ,
, 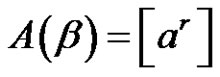 , then by (1.7), the solutions of
, then by (1.7), the solutions of  in
in 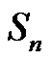 are
are
a)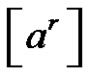 , if
, if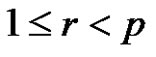 , or
, or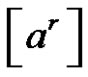
b) 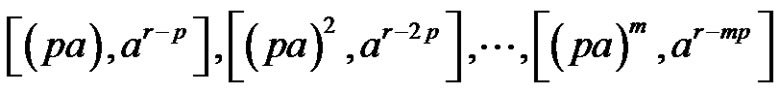 if
if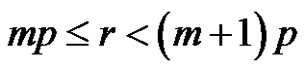 .
.
1) Assume 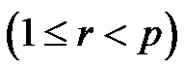 and (a is odd or (a and r) are even), then from a),
and (a is odd or (a and r) are even), then from a), 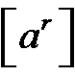 is the solution set of
is the solution set of  in
in . Let
. Let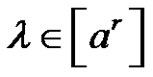 . If a is odd and
. If a is odd and where
where 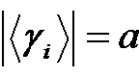 (odd) for each
(odd) for each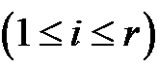 , then
, then 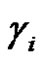 is a product of an even number similar to
is a product of an even number similar to  of transpositions for all
of transpositions for all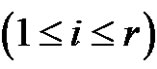 . For any r (odd or even),
. For any r (odd or even), 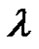 is a product of
is a product of 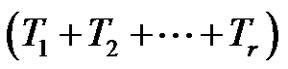 = (even) number of transpositions
= (even) number of transpositions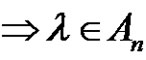 . If a and r are even and
. If a and r are even and , where
, where  (even) for each
(even) for each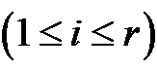 , then
, then 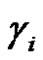 is a product of an odd number similar to
is a product of an odd number similar to 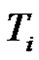 of transpositions for all
of transpositions for all 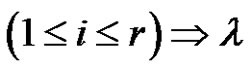 is a product of
is a product of
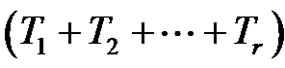 = (even) number of transpositions
= (even) number of transpositions 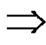
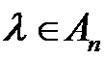 , then the solution set of
, then the solution set of 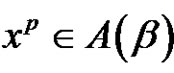 in An is
in An is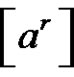 .
.
2) Assume [(a and p) are odd) or (p is odd and (a and r) are even)] and 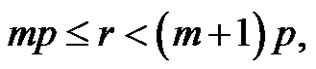 then from b),
then from b),
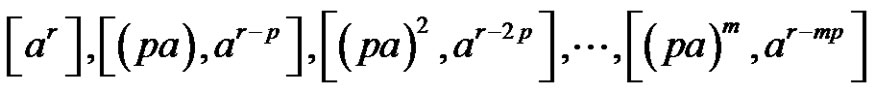
are solutions of  in Sn. Let
in Sn. Let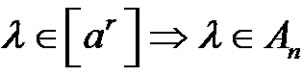 , considering that (a is odd or (a and r) are even) and for each
, considering that (a is odd or (a and r) are even) and for each 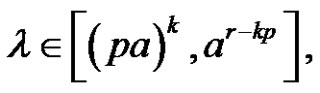
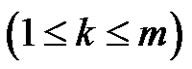 . If a and p are odd, then
. If a and p are odd, then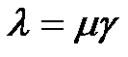 , where
, where 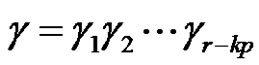 and
and
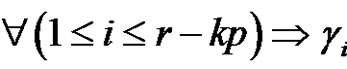
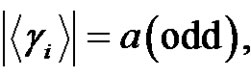 is a product of an even number of transpositions for all,
is a product of an even number of transpositions for all, 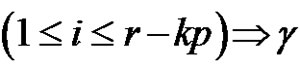 is a product of an even number of transpositions, and
is a product of an even number of transpositions, and
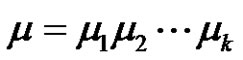 , where
, where 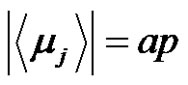 (odd),
(odd),
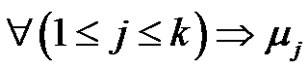 is a product of an even number of transpositions for all and
is a product of an even number of transpositions for all and 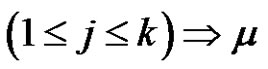 is a product of an even number of transpositions
is a product of an even number of transpositions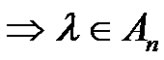 . If (p is odd and (a and r) are even), then
. If (p is odd and (a and r) are even), then 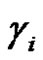 is a product of an odd number similar to Li of transpositions,
is a product of an odd number similar to Li of transpositions,
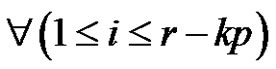 . Moreover,
. Moreover,  (even), and
(even), and
 is a product of an odd number similar to
is a product of an odd number similar to 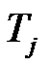 of transpositions for all
of transpositions for all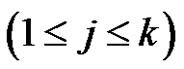 . If k is odd, then
. If k is odd, then 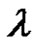 is a product of
is a product of 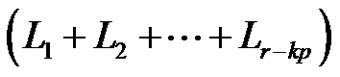 +
+ 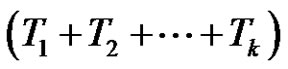 = (odd) + (odd) = (even) number of transpositions
= (odd) + (odd) = (even) number of transpositions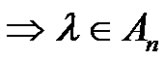 . If k is even, then
. If k is even, then  is a product of
is a product of  +
+ 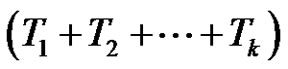 = (even) + (even) = (even) number of transpositions
= (even) + (even) = (even) number of transpositions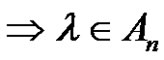 , then the solutions of
, then the solutions of  in
in 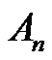 are
are
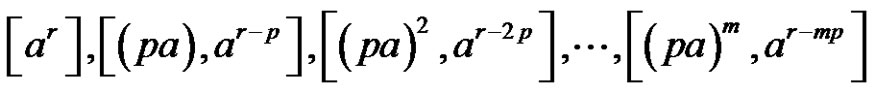 .
.
3) and 4) Assume [(a is odd and p is even) or (a, p, and r are even)] and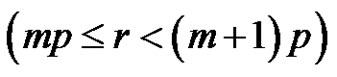 . Then, from b),
. Then, from b),  ,
, 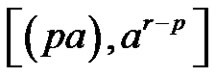 , and
, and 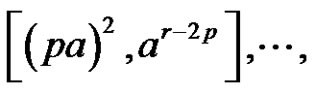
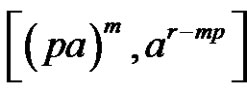 are solutions of
are solutions of  in
in . Let
. Let , [a is odd or (a and r) are even]. For each
, [a is odd or (a and r) are even]. For each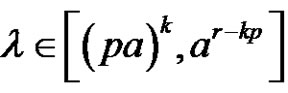 ,
, 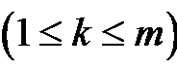 if (a is odd and p is even)
if (a is odd and p is even)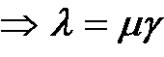 , where
, where 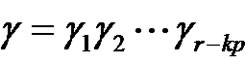 and
and 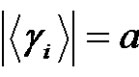 (odd),
(odd), 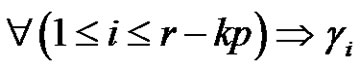 is a product of an even number similar to
is a product of an even number similar to 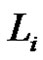 of transpositions,
of transpositions, 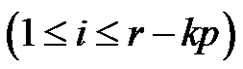 and
and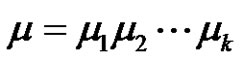 , where
, where 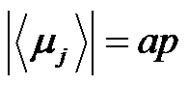 (even),
(even),
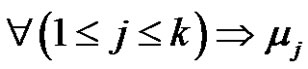 is a product of an odd number similar to
is a product of an odd number similar to  of transpositions for all
of transpositions for all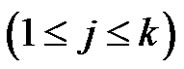 . If k is odd, then
. If k is odd, then 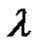 is a product of
is a product of  +
+ 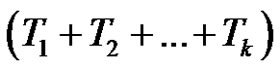 = (even) + (odd) = (odd) number of transpositions
= (even) + (odd) = (odd) number of transpositions . If k is even, then
. If k is even, then 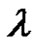 is a product of
is a product of 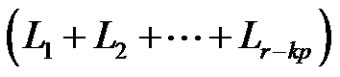 +
+ 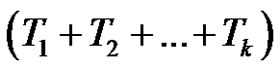 = (even) + (even) = (even) number of transpositions
= (even) + (even) = (even) number of transpositions 
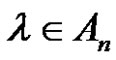 . If (a, p, and r are even), then
. If (a, p, and r are even), then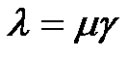 , where
, where 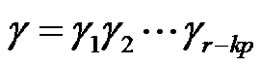 and
and 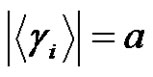 (even),
(even),
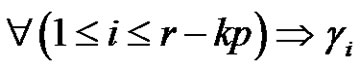 is a product of an odd number similar to
is a product of an odd number similar to 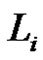 of transpositions,
of transpositions, 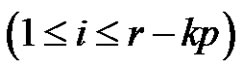 and
and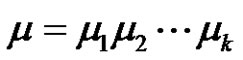 , where
, where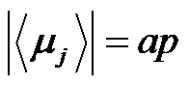 (even),
(even),
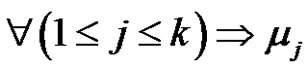 is a product of an odd number similar to
is a product of an odd number similar to 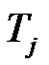 of transpositions for all
of transpositions for all . If k is odd, then
. If k is odd, then  is a product of
is a product of 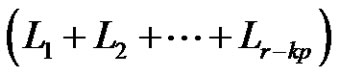 +
+  = (even) + (odd) = (odd) number of transpositions
= (even) + (odd) = (odd) number of transpositions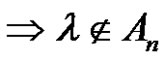 . If k is even, then
. If k is even, then 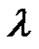 is a product of
is a product of 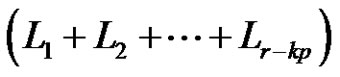 +
+ 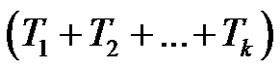 = (even) + (even) = (even) number of transpositions
= (even) + (even) = (even) number of transpositions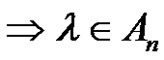 , then the solutions of
, then the solutions of 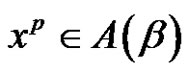 in
in  are
are
 (if m is even) and
(if m is even) and
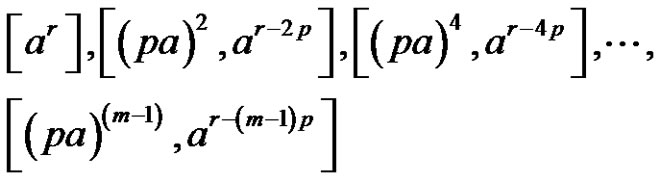
(if m is odd).
5) and 6) Assume [(a and p) are even and r is odd)] and . From b),
. From b),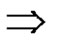
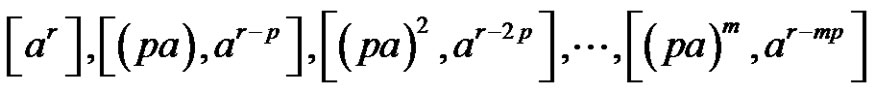 are solutions of
are solutions of 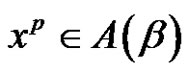 in
in . Let
. Let
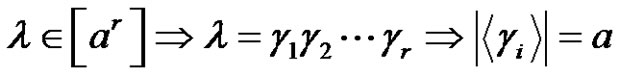 (even),
(even),
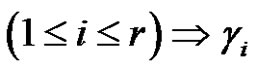 is a product of an odd number similar to
is a product of an odd number similar to  of transpositions for all,
of transpositions for all, 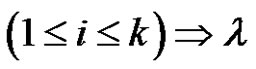 is a product of
is a product of 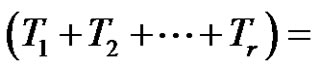 (odd) number of transposetions, also for each
(odd) number of transposetions, also for each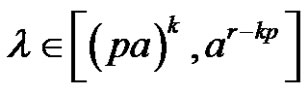 , where
, where
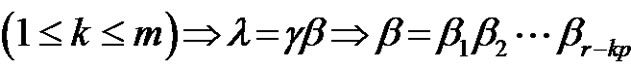 , where
, where 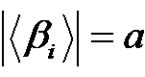 (even),
(even), 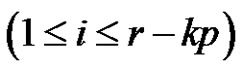 and
and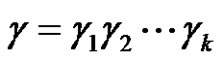 , where
, where
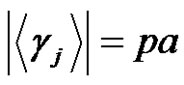 (even)
(even)  is product of an odd number similar to
is product of an odd number similar to 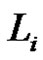 of transpositions for each
of transpositions for each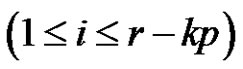 , and
, and 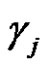 is product of an odd number similar to
is product of an odd number similar to 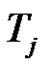 of transpositions for each
of transpositions for each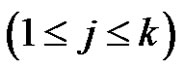 . If k is odd, then
. If k is odd, then  is a product of
is a product of 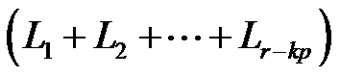 +
+  = (odd) + (odd) = (even) number of transpositions
= (odd) + (odd) = (even) number of transpositions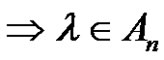 . If k is even, then
. If k is even, then 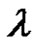 is a product of
is a product of 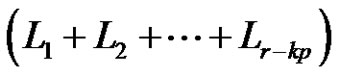 +
+ 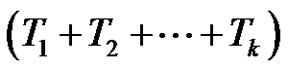 = (odd) + (even) = (odd) number of transpositions
= (odd) + (even) = (odd) number of transpositions 
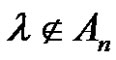 . Then, if [(a and p) are even and r is odd)] and
. Then, if [(a and p) are even and r is odd)] and , then the solutions of
, then the solutions of 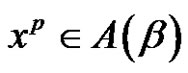 in
in 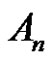 are
are
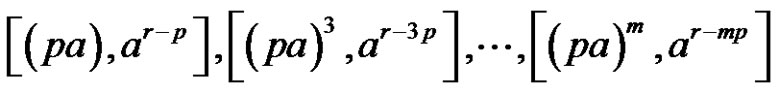 (if m is odd), or
(if m is odd), or
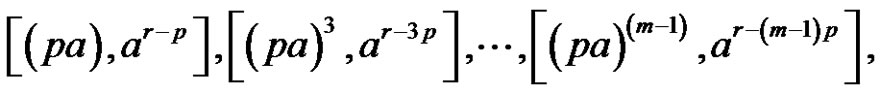
(if m is even).
7) Assume (a is even and (p and r) are odd). For each 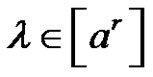 or
or 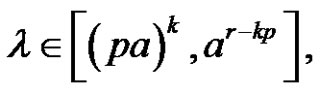
 , then there is no solution of
, then there is no solution of 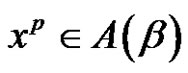 in
in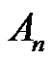 .
.
3.2. Remarks
Let p and q be different prime numbers and  a conjugate class of symmetric group. If
a conjugate class of symmetric group. If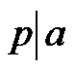 ,
, 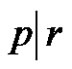 and q does not divide a we defined collection of sets of conjugate classes of
and q does not divide a we defined collection of sets of conjugate classes of 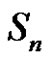 as following:
as following:
1) 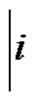
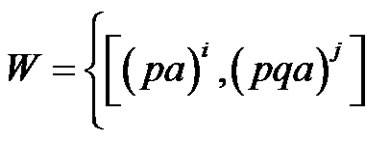 and j are non-negative and solutions of the equation
and j are non-negative and solutions of the equation 
2) 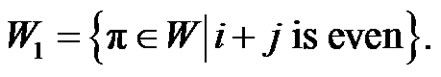
3) 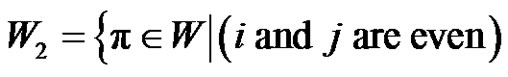
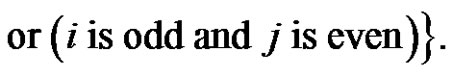
4) 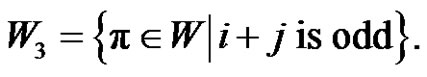
5) 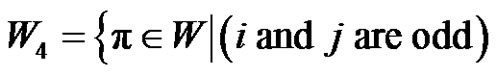
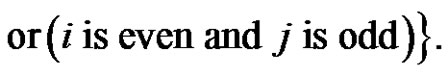
*We note that  &
& 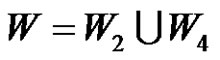
** ,
,
 ,
, 
 ,
,

3.3. Remarks
1) If a, p and q are odd, then for each , where
, where 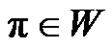 we have
we have 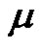 is even.
is even.
2) If a is even, then for each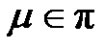 , where
, where 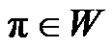 we have (
we have (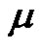 is even if
is even if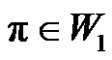 ) and (
) and ( is odd if
is odd if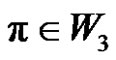 ).
).
3) If p is even, then for each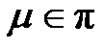 , where
, where 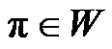 we have (
we have (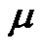 is even if
is even if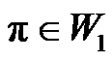 ) and (
) and ( is odd if
is odd if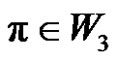 ).
).
4) If q is even and a, p are odd, then for each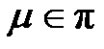 , where
, where 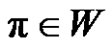 we have (
we have ( is even if
is even if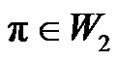 ) and (
) and ( is odd if
is odd if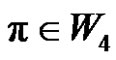 ).
).
3.4. Theorem
Let 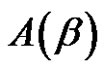 be a conjugacy class of
be a conjugacy class of 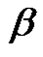 in
in , and
, and
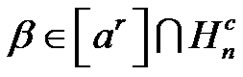 , where
, where 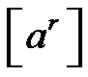 is a class of
is a class of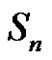 . If p and q are different two prime numbers and
. If p and q are different two prime numbers and  and q does not divide a, then the solutions of
and q does not divide a, then the solutions of 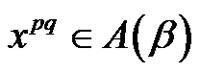 in
in 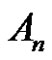 are:
are:
1) W if 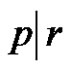 and (a, p and q are odd).
and (a, p and q are odd).
2) 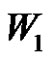 if
if  and (a or p is even).
and (a or p is even).
3) 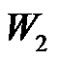 if
if 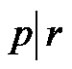 and (q is even & (a and p) are odd).
and (q is even & (a and p) are odd).
4) Not exist if p does not divide r.
5) Not exist if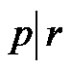 , (a or p is even) and
, (a or p is even) and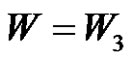 .
.
6) Not exist if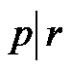 , (q is even & (a and p) are odd) and
, (q is even & (a and p) are odd) and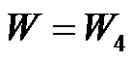 .
.
Proof:
Since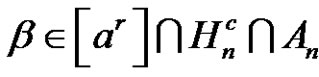 ,
, 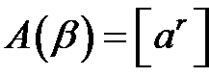 and by (1.8) we have that the solution of
and by (1.8) we have that the solution of 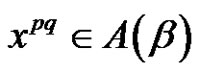 in
in 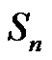 is:
is:
a) W if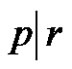 .
.
b) Not exist if p does not divide r.
1) Assume 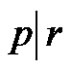 and (a, p and q are odd). Then from a) we have W is the solution set of
and (a, p and q are odd). Then from a) we have W is the solution set of 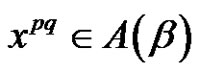 in
in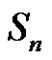 . Let
. Let  for each
for each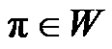 , we have
, we have 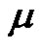 is even permutation Then the solution set in
is even permutation Then the solution set in 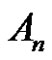 is W.
is W.
2) Assume 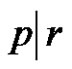 and (a or p is even). Then from a) we have W is the solution set of
and (a or p is even). Then from a) we have W is the solution set of 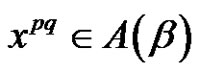 in
in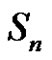 . Let
. Let 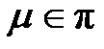 for each
for each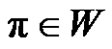 , we have (
, we have (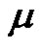 is even permutation, if
is even permutation, if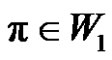 ) and (
) and (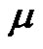 is odd permutation, if
is odd permutation, if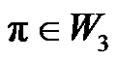 ). Then the solution set in
). Then the solution set in 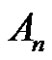 is
is 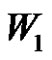 .
.
3) Assume 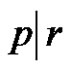 and (q is even & (a and p) are odd). Then from a) we have W is the solution set of
and (q is even & (a and p) are odd). Then from a) we have W is the solution set of 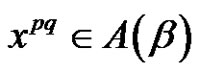 in
in . Let
. Let 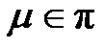 for each
for each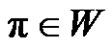 , we have (
, we have (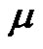 is even permutation, if
is even permutation, if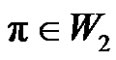 ) and (
) and (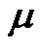 is odd permutation, if
is odd permutation, if ). Then the solution set in
). Then the solution set in 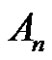 is
is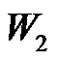 .
.
4) Assume p does not divide r. Then from b) we have no solution of 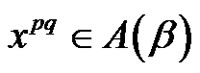 in
in 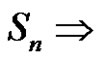 no solution of
no solution of  in
in .
.
5) and 6) it is clear if , (a or p is even) and
, (a or p is even) and , then
, then 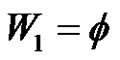 and there exists no solution in
and there exists no solution in , also if
, also if , (q is even & (a and p) are odd) and
, (q is even & (a and p) are odd) and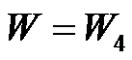 , then
, then 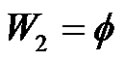 and there exists no solution in
and there exists no solution in .
.
3.5. Remarks
Let p and q be two different prime numbers and 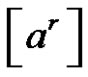 a conjugate class of symmetric group
a conjugate class of symmetric group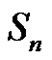 , p does not divide a and q does not divide a we defined a collection of sets of conjugate classes of
, p does not divide a and q does not divide a we defined a collection of sets of conjugate classes of  as following:
as following:
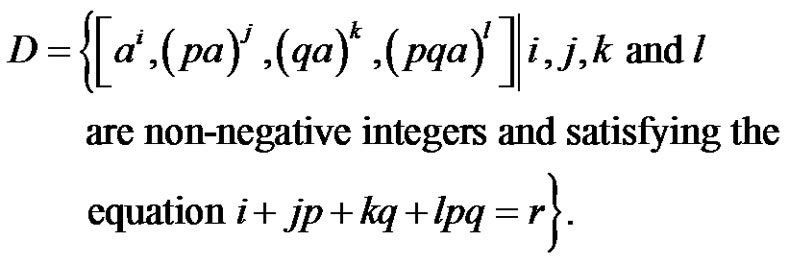
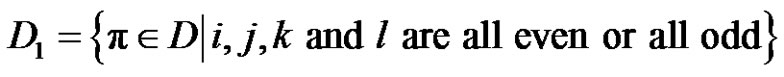 .
.
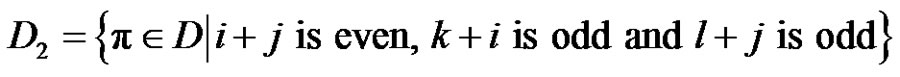 .
.
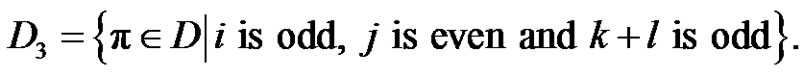
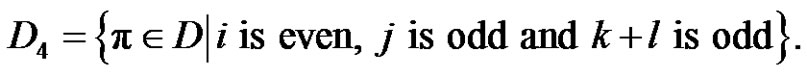
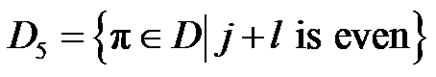 .
.
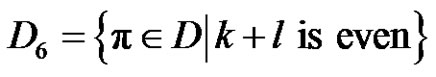 .
.
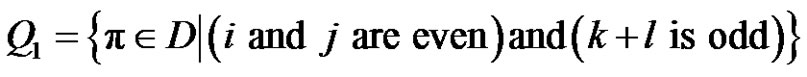 .
.
 .
.
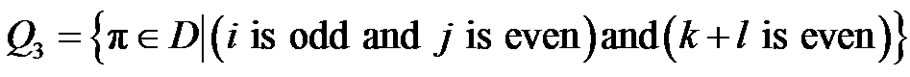 .
.
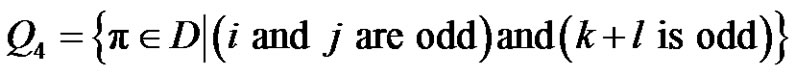 .
.
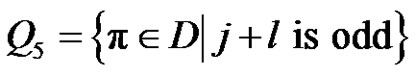 .
.
 .
.
We can denote D as the following:
• 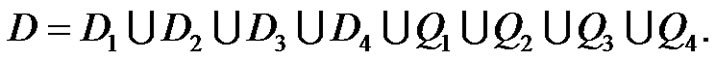
• 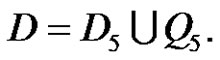
•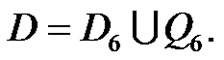
3.6. Remarks
1) If a, p and q are odd, then for each , where
, where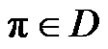 ,
, 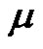 is even.
is even.
2) If a is even, then for each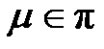 ,
, 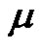 is even if
is even if  and
and 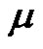 is odd if
is odd if 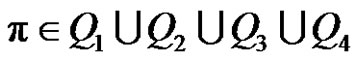 .
.
3) If p is even and (a and q) are odd, then for each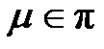 ,
, 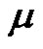 is even if
is even if 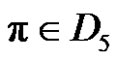 and
and 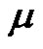 is odd if
is odd if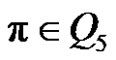 .
.
4) If q is even and (a and p) are odd, then for each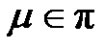 ,
, 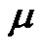 is even if
is even if 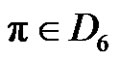 and
and 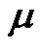 is odd if
is odd if .
.
3.7. Theorem
Let 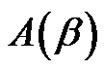 be the conjugacy class of
be the conjugacy class of 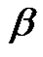 in
in , and
, and , where
, where 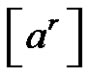 is a class of
is a class of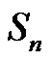 , p and q are different two prime numbers. If p does not divide a and q does not divide a, then the solution of
, p and q are different two prime numbers. If p does not divide a and q does not divide a, then the solution of  in
in 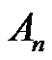 is
is
1) D, if a, p and q are odd
2) , where
, where , if a is even
, if a is even
3)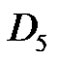 , if a and q are odd, and p is even
, if a and q are odd, and p is even
4)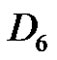 , if a and p are odd, and q is even
, if a and p are odd, and q is even
5) does not exist, ifaiseven, and
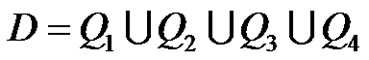
6) does not exist, if p is even, a and q are odd, and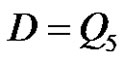 , or
, or
7) does not exist, if q is even, a and p are odd, and .
.
Proof
Considering that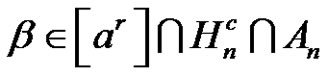 ,
,  then by (2.2.11), D is the solution set of
then by (2.2.11), D is the solution set of 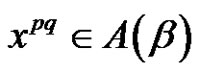 in
in .
.
1) Assume a, p and q are odd. Let 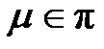 for each
for each 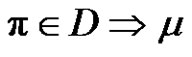 is even
is even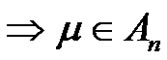 . Then the solution set in
. Then the solution set in 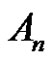 is D if a, p and q are odd.
is D if a, p and q are odd.
2) Assume a is even. Let 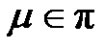 for each
for each 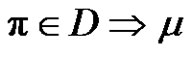 is even
is even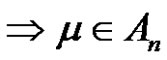 . Then the solution set in
. Then the solution set in  is
is , if a is even.
, if a is even.
3) Assume a and q are odd, and p is even. Let 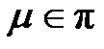 for each
for each 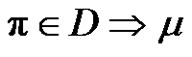 is even
is even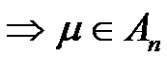 . Then the solution set in
. Then the solution set in  is
is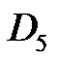 , if a and q are odd, and p is even.
, if a and q are odd, and p is even.
4) Assume a and p are odd, and q is even. Let 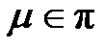 for each
for each 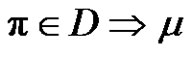 is even
is even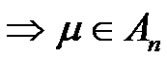 . Then the solution set in
. Then the solution set in 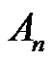 is
is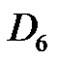 , if a and p are odd, and q is even.
, if a and p are odd, and q is even.
5) Assume a is even and 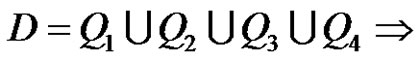
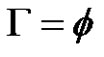 . Then there is no solution in
. Then there is no solution in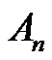 .
.
6) and 7) Assume a and q are odd, p is even, and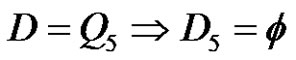 . Then there is no solution in
. Then there is no solution in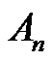 , also if a and p are odd, q is even, and
, also if a and p are odd, q is even, and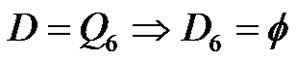 . Then there is no solution in
. Then there is no solution in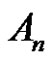 .
.
3.8. The Number of the Solutions
Assume 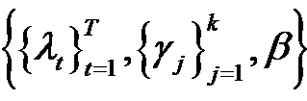 are even permutations where
are even permutations where 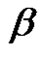 and
and 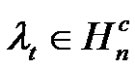 and
and 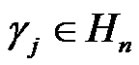 for all 1 ≤ t ≤ T and 1 ≤ j ≤ k. Then we can find the number of the solutions of class equation
for all 1 ≤ t ≤ T and 1 ≤ j ≤ k. Then we can find the number of the solutions of class equation 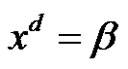 in
in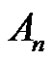 , where d is a positive integer number as follow:
, where d is a positive integer number as follow:
1) If  are the solutions, then the number of solutions set is
are the solutions, then the number of solutions set is
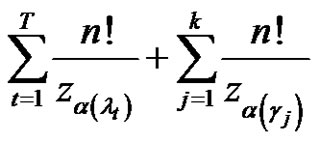
2) If  are the solutions, then the number of solutions set is
are the solutions, then the number of solutions set is
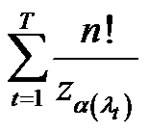
3) If  are the solutions, then the number of solutions set is
are the solutions, then the number of solutions set is
 .
.
3.9. Example
Find the solutions of 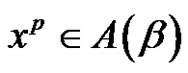 in
in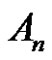 , and the number of the solutions.
, and the number of the solutions.
1) If p = 3 and 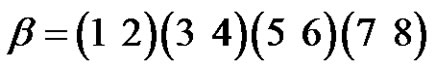 in
in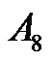 .
.
2) If p = 2 and 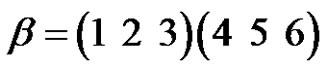 in
in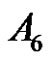 .
.
Solution:
1) Since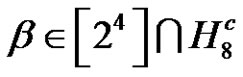 , a = 2, r = 4, p does not divide a,
, a = 2, r = 4, p does not divide a,  where, m = 1.
where, m = 1.
So a and r are even, and p is odd. Then by (3.1) the solutions of 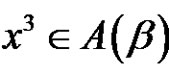 in
in 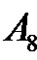 are
are  and
and , so the number of solutions is
, so the number of solutions is 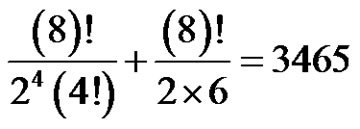 permutations.
permutations.
2) Since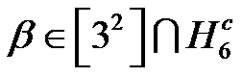 , a = 3, r = 2, p does not divide a,
, a = 3, r = 2, p does not divide a,  where, m = 1.
where, m = 1.
Also, since a is odd and p is even. Then by (3.1) the solution set of  in
in  is
is . So the number of solutions is
. So the number of solutions is 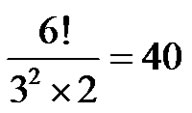 permutations.
permutations.
3.10. Remark
If 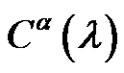 conjugate class of
conjugate class of 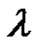 in
in 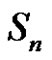 belong to the solution set of class equation
belong to the solution set of class equation 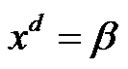 in An and
in An and , then we denote to this set
, then we denote to this set 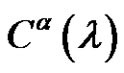 by
by 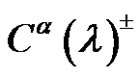 or
or
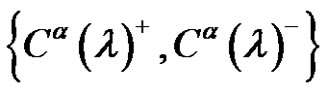 .
.
3.11. Example
Find the solution of

in  and the number of the solutions.
and the number of the solutions.
Solution:
Let 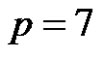 and
and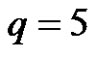 , since
, since
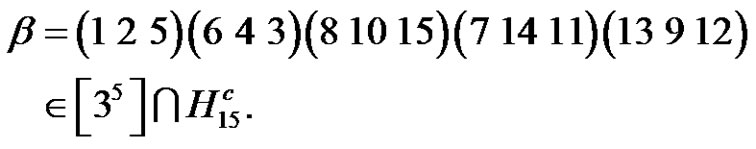
Then by (3.7) the solutions of
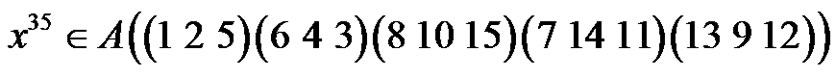
in 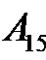 are
are ,
, 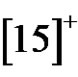 and
and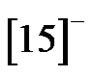 . So the number of the solutions set is
. So the number of the solutions set is  permutations.
permutations.
4. Concluding Remarks
By the Cayley’s theorem: Every finite group G is isomorphic to a subgroup of the symmetric group , for some
, for some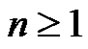 . Then we can discuss these propositions. Let
. Then we can discuss these propositions. Let 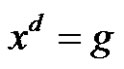 be class equation in finite group G and assume that
be class equation in finite group G and assume that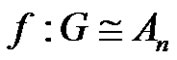 , for some
, for some 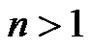 and
and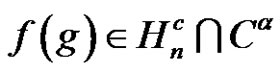 . The first question we are concerned with is: What is the possible value of d provided that there is no solution for
. The first question we are concerned with is: What is the possible value of d provided that there is no solution for 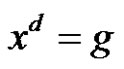 in G? The second question we are concerned with is: what is the possible value of d provided that there is a solution for
in G? The second question we are concerned with is: what is the possible value of d provided that there is a solution for 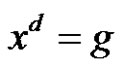 in G? And then we can find the solution and the number of the solution for
in G? And then we can find the solution and the number of the solution for  in G by using Cayley’s theorem and our theorems in this paper. In another direction, let G be a finite group, and
in G by using Cayley’s theorem and our theorems in this paper. In another direction, let G be a finite group, and 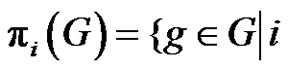 the least positive integer number satisfy
the least positive integer number satisfy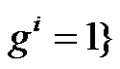 . If
. If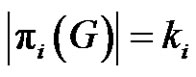 , then we write
, then we write
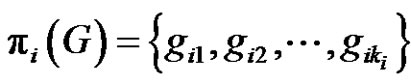 and
and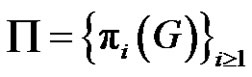 . For each
. For each
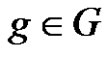 and
and 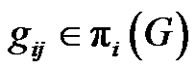 we have
we have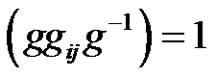 . By the Cayley’s theorem we can suppose that
. By the Cayley’s theorem we can suppose that 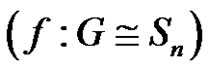 or
or . Also the questions can be summarized as follows:
. Also the questions can be summarized as follows:
1) Is 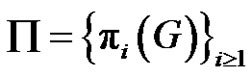 collection set of conjugacy classes of G?
collection set of conjugacy classes of G?
2) Is there some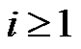 , such that
, such that  for each
for each 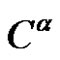 of
of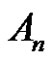 , where
, where ?
?
3) Is there some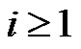 , such that
, such that  for each
for each 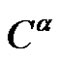 of
of , where
, where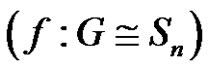 ?
?
4) If 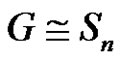 and
and 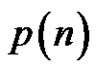 is the number of partitions of n, is
is the number of partitions of n, is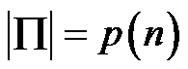 ?
?
5) If 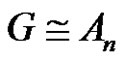 and
and  has m ambivalent conjugacy classes. It is true that is also necessarily G has m ambivalent conjugacy classes?
has m ambivalent conjugacy classes. It is true that is also necessarily G has m ambivalent conjugacy classes?
Finally we will discuss if there is any relation between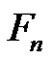 ,
, 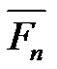 and
and 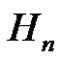 in
in 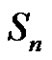 and what is the possible value of d provided that there is a solution for
and what is the possible value of d provided that there is a solution for 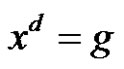 in G where
in G where 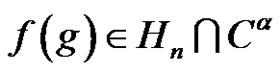 and for some n to be:
and for some n to be:
1)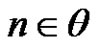 .
.
2)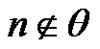 .
.
REFERENCES
- H. Ishihara, H. Ochiai, Y. Takegahara and T. Yoshida, “p-divisibility of the number of solutions of xp = 1 in a symmetric group,” Annals of Combinatorics, Vol. 5, No. 2, 2001, pp. 197-210. doi:10.1007/PL00001300
- N. Chigira, “The solutions of xd = 1 in Finite Groups,” Journal of Algebra, Vol. 180, No. 3, 1996, pp. 653-661. doi:10.1006/jabr.1996.0086
- R. Brauer, “On a theorem of Frobenius,” American Mathematical Monthly, Vol. 76, No. 1, 1969, pp. 12-15. doi:10.2307/2316779
- Y. G. Berkovich, “On the number of elements of given order in finite p-group,” Israel Journal of Mathematics, Vol. 73, No. 1, 1991, pp. 107-112. doi:10.1007/BF02773429
- T. Ceccherini-Silberstein, F. Scarabotti and F. Tolli, “Representation Theory of the Symmetric Groups,” Cambridge University Press, New York, 2010.
- D. Zeindler, “Permutation matrices and the moments of Their Characteristic Polynomial,” Electronic Journal of Probability, Vol. 15, No. 34, 2010, pp. 1092-1118.
- J. J. Rotman, “An introduction to the theory of groups,” 4th Edition, Springer-Verlag, New York, 1995.
- G. D. James and A. Kerber, “The Representation Theory of the Symmetric Group,” Addison-Wesley Publishing, Boston, 1984.
- S. A. Taban, “Equations in Symmetric Groups,” Ph.D. Thesis, University of Basra, Basra, 2007.
- S. Mahmood and A. Rajah, “Solving the Class Equation xd = β in an Alternating Group for each
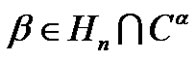 and
and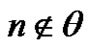 ,” Journal of the Association of Arab Universities for Basic and Applied Sciences, Vol. 10, No. 1, 2011, pp. 42-50. doi:10.1016/j.jaubas.2011.06.006
,” Journal of the Association of Arab Universities for Basic and Applied Sciences, Vol. 10, No. 1, 2011, pp. 42-50. doi:10.1016/j.jaubas.2011.06.006

