Computational Molecular Bioscience
Vol.07 No.03(2017), Article ID:78476,13 pages
10.4236/cmb.2017.73003
Stability Analysis for the Cellular Signaling Systems Composed of Two Phosphorylation-Dephosphorylation Cyclic Reactions
Chinasa Sueyoshi1, Takashi Naka2
1Graduate School of Information Science, Kyushu Sangyo University, Fukuoka, Japan
2Department of Information Science, Kyushu Sangyo University, Fukuoka, Japan
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/
Received: June 30, 2017; Accepted: August 13, 2017; Published: August 16, 2017
ABSTRACT
The regulatory mechanisms in cellular signaling systems have been studied intensively from the viewpoint that the malfunction of the regulation is thought to be one of the substantial causes of cancer formation. On the other hand, it is rather difficult to develop the theoretical framework for investigation of the regulatory mechanisms due to their complexity and nonlinearity. In this study, more general approach is proposed for elucidation of characteristics of the stability in cellular signaling systems by construction of mathematical models for a class of cellular signaling systems and stability analysis of the models over variation of the network architectures and the parameter values. The model system is formulated as regulatory network in which every node represents a phosphorylation-dephosphorylation cyclic reaction for respective constituent enzyme. The analysis is performed for all variations of the regulatory networks comprised of two nodes with multiple feedback regulation loops. It is revealed from the analysis that the regulatory networks become mono-stable, bi-stable, tri-stable, or oscillatory and that the negative mutual feedback or positive mutual feedback is favorable for multi-stability, which is augmented by a negatively regulated node with a positive auto-regulation. Furthermore, the multi-stability or the oscillation is more likely to emerge in the case of low value of the Michaelis constant than in the case of high value, implying that the condition of higher saturation levels induces stronger nonlinearity in the networks. The analysis for the parameter regions yielding the multi-stability and the oscillation clarified that the stronger regulation shifts the systems toward multi-stability.
Keywords:
Cellular Signaling Systems, Regulatory Networks, Cyclic Reaction, Michaelis-Menten Mechanism, Multi-Stability, Oscillation
1. Introduction
Cellular signaling systems have been studied extensively from the recent viewpoint that their disorder is thought to be one of the causes for cancer formation since the systems are known to regulate biochemical reactions operating in cells for various functions such as cell differentiation, cell proliferation, and homeostasis. Figure 1(a) displays MAPK (Mitogen-activated Protein Kinase) cascade which is one of the typical cellular signaling systems, and has been studied intensively, elucidating the various regulatory characteristics for activities of living cells such as the switch-like responses, bi-stability, oscillations, robustness, and so on [1] - [6] . The cellular signaling systems are comprised of enzymatic reactions such as phosphorylation-dephosphorylation cyclic reactions which are primary components of MAPK cascade as seen in Figure 1(a). Cyclic reaction
Figure 1. Regulatory network for MAPK cascade. (a): The MAPK cascade which is composed of several cyclic reactions with a feedback regulation from MAPK-PP; (b): Simplified version of the MAPK cascade.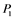
, 
, 
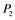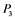, and 
correspond to active Ras, Raf, Mek, and Erk, respectively, while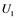
, 
, 
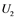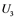, and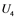 
are inactive forms of those enzymes; (c): Regulatory network representing the MAPK cascade. Each node represents the cyclic reaction in (b); (d): Cyclic reaction in node i.
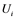: inactive form of enzyme at node i;
: active form of enzyme at node i;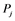
: activating enzyme for
;
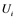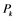: inactivating enzyme for
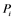. The rate constant for the activation and the inactivation are denoted by 
and
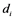, respectively.
seems to be primary reaction system for other cellular signaling systems such as Rac1, PAK, and RhoA signaling networks [7] .
Many studies have employed simulation analysis with the given values for the parameters in the signaling systems because of the difficulty in developing the analytical method for the systems analysis due to their nonlinearity. In this study, more general approach is proposed for characterization of the stability in cellular signaling systems by construction of mathematical models for a class of cellular signaling systems and simulation analysis of the models over variation of the network architectures and the values of parameters. The model system is formulated as regulatory network in which every node represents an activation-inactivation cyclic reaction for respective constituent enzyme of the network and the regulatory interactions between the activated enzyme and the reaction are depicted by arcs between nodes. The Michaelis-Menten mechanism is assumed for the reaction paths in each cyclic reaction and the emergence of the stable point in steady states of the network is analyzed.
It is biologically significant to analyze the characteristics of the stability in cellular signaling systems since stable points are convergent states of the relaxation process in dynamic changes due to random noises, and seem to correspond to the distinct biochemical states such as normal states or malfunctional states. Similar approaches have been taken in several studies [5] [8] - [15] . Kuwahara et al. applied the rather simpler regulatory networks to elucidate the effects of network architectures on the stochastic characteristics [8] . Ma et al., Yao et al., and Adler et al. employed the similar regulatory networks of three nodes, but focused on the biochemical adaptation mechanisms, robust and resettable bi-stability, and fold-change detection mechanism for living cells, respectively [9] [14] [15] .
In this study the stability analysis is performed for all variations of the regulatory networks comprised of two nodes with multiple feedback regulation loops.
2. Results
2.1. Formulation of Regulatory Networks for Cellular Signaling Systems
The regulatory network is formulated as follows. Every node represents an activation-inactivation cyclic reaction for respective constituent enzyme of the network. The activated enzyme in a node acts on another node for the positive regulation which increases the active enzyme or for the negative regulation which increases the inactive enzyme through the reverse path. The regulatory interactions between the activated enzyme and the reaction are depicted by arcs between nodes. The MAPK cascade is comprised of several cyclic reactions and has a feedback regulation from MAPK-PP as shown in Figure 1(a). Figure 1(b) is a simplified representation of the MAPK cascade of Figure 1(a). Figure 1(c) illustrates the regulatory network of the MAPK cascade, which is analyzed in this study.
Figure 1(d) shows a cyclic reaction in node i which is regulated positively by node j, and negatively by node k. We assume the Michaelis-Menten mechanism as the reaction mechanism in the cyclic reactions and the reaction rate equations are formulated as Equations (1)-(5):
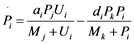(1)
(2)
(3)
(4)
(5)
It should be noted that the Michaelis-Menten equation is adopted as the reaction mechanism, and therefore, the enzyme-substrate complex does not appear in the reaction rate equations. 
is the total concentration of enzyme 
in node i and 
is the relative concentration of
. 
and 
are the normalized Michaelis constants of enzymes 
and
, respectively. In addition to 
and
, the normalized rate Equation (4) has a parameter
, which is the ratio of maximum inactivation velocity to maximum activation velocity. The value of 
is set to be unity in the case of no positive regulation for node i, whereas the value of 
is set to be unity in the case of no negative regulation.
We analyze the characteristics of stability for all variations of two-node regulatory networks with multiple feedback regulation loops under the restriction that each node has at most one positive regulation and one negative regulation as designated in Figure 2.
Figure 2. Regulatory networks with feedback regulations. Red arrows and blue arrows depict the positive and negative regulations, respectively. The number in each node corresponds to the parameter 
or 
in the graphs of parameter space as shown in Figure 4 and Figure 5.
2.2. Characteristics of Multi-Stability in the Regulatory Networks
In Figure 3 the effects of Michaelis constant on the emergence ratio of multi- stable state are demonstrated for each regulatory network examined. It follows from this figure that the networks are divided into two groups; that is, the networks with high emergence ratio (F, G, H, I, J) and those with zero or slight emergence ratio (A, B, C, D, E). The former group is further categorized into those with very high emergence ratio (I, J) and those with moderate emergence ratio (F, G, H). The latter group also is further assorted into the networks with zero emergence ratio (A, B, C) and slight emergence ratio (D, E). It is observed that the emergence ratio decreases when the Michaelis constant gets higher, and then it converges at certain levels for the networks with very high emergence ratio. On the other hand, multi-stable state arises when the Michaelis constant is low, and then the ratios become zero for the networks with the moderate emergence ratio. The highest emergence ratio at Michaelis constant of 
is 100%, 69.4%, 25.6%, 19.0%, and 16.5% for the networks J, I, H, G, and F, respectively. Regarding the networks E and D, the highest ratio of 1.7% is attained at Michaelis constant of 
and
, respectively.
In Figure 4 the distributions of multi-stable equilibrium points in the parameter space of 
and 
are illustrated for each regulatory network and various Michaelis constants examined. The heat maps in Figure 4 mean the sensitivities which quantify the effect of the change of parameter values on the set of stable equilibrium points. The precise definition of the sensitivity is provided in the method section. The blue area corresponds to the zero or slight sensitivities, implying that the set of stable equilibrium points hardly change in the area. In contrast, the red area indicates high sensitivity where the set changes drastically.
It should be noted that, as the networks G, H, and J are symmetric for each node, the graphs for these networks are symmetric to the diagonal line. It is revealed that bi-stable states appear in the area with low values of 
for the network G which is composed of mutual negative feedbacks. In contrast, bi-stable states are likely to appear in the area with high values of 
for the
Figure 3. Emergence ratio of multi-stability for the regulatory networks. The abscissa depicts each regulatory network and the ordinate represents logarithm values of base 2 for the normalized Michaelis constant L. The applicate axis represents the emergence ratio.
Figure 4. Distributions of multi-stable equilibrium points and the sensitivities for each regulatory network in the parameter space. Each column corresponds respectively to the individual regulatory networks of D, E, F, G, H, I, and J for which multi-stability emerges. L denotes the normalized Michaelis constant. The abscissa and the ordinate in each small graph depict the logarithm values of base 2 for 
and
, respectively. The subscripts of K correspond to the numbers in the nodes in Figure 2. Orange circle marks and blue triangle marks locate the bi-stable points and tri-stable points, respectively. Green cross marks in the graphs for network D depict the oscillation points for the values between 
and
. The sensitivities of a set of equilibrium points to the change of parameter values of 
and 
are displayed as the heat maps in which light blue shows low sensitivity and purple indicates high sensitivity. The white areas in the graph for network H and 
correspond to the points in which real part of one of the eigenvalues are zero. The five graphs in the bottom row except the leftmost one show the values of the stable equilibrium points in each light blue area of upper graphs indicated by the corresponding alphabetic letters below where the points are indicated by circles, while the leftmost one demonstrates the values of equilibrium points in 
-plane in subgraphs in the right four graphs.
networks H and J which contain mutual positive feedbacks. Since the parameter 
is the maximum velocity of inactivation divided by that of activation, higher and lower values of 
enforce negative regulations and positive regulations, respectively. Therefore, bi-stable state is likely to appear in the area where the regulations are enforced.
The bi-stable area for lower value of the Michaelis constant include the area for higher value of the Michaelis constant for the network F, G, H, I, and J, that is consistent with the tendency that lower value of the Michaelis constant is favorable to emergence of multi-stable state shown in Figure 3. Likewise, tri-stable states in the area with low values of 
of network J gets smaller with lower value of the Michaelis constant, and then vanishes at L = 20.
It follows from Figure 4 that the parameter space is divided into the robust several subspaces according to the change in 
and bifurcation occurs on the high sensitive purple area across the low sensitive light blue area. The set of stable equilibrium points in the light blue areas contains the combinations of nearly zero or nearly unity values of 
or
. The graphs in the bottom row explain these combinations for each graph in the upper rows. The values under 0.1 and the values over 0.9 are regarded as zero and unity, respectively, in these graphs. It is noted that the networks with mutual positive feedbacks yield the bi-stable state in which the both of two nodes are fully activated or fully inactivated, while the networks with mutual negative feedbacks yield the bi-stable state in which either of the nodes is fully activated and the other node is fully inactivated in the parameter space with high or moderate values of
. On the other hand, both of the two nodes are fully activated in the areas with low values of 
for all the networks examined. This feature is predictable since the low value of 
enforces the activation, and it seems capable to yield the tri-stable equilibrium points in network J.
The white area in the graph at 
for the network H indicates that the set of stable equilibrium points is empty since the eigenvalues of this point are −2 and 0. Likewise, the white areas in the graphs for the network D depict the empty set of stable equilibrium points because of the oscillations.
2.3. Characteristics of Oscillations in the Regulatory Networks
Figure 5 displays the limit cycles for the oscillations indicated by green cross marks in the graphs for network D in Figure 4. It is observed that the oscillation area for lower value of the Michaelis constant includes the area for higher value of the Michaelis constant as in the case of multi-stability. Furthermore, oscillation arises in the case that 
is less than unity. It seems difficult to find out the simple rules for the locations and the sizes of limit cycles with respect to the value of Michaelis constant L; however, the size of the limit cycle for each L value is getting bigger with higher
, and then getting smaller, suggesting that the optimal value of 
seems to exist to maximize the size of the limit cycle for each L value. It is also seen that the almost of all limit cycles appear in the
Figure 5. The characteristics of the limit cycles in Network D. The abscissa depicts the parameter values of 
and the ordinate denotes the values of the normalized Michaelis constant L. The parameter values of 
is 20 except the three graphs in second row and two graphs in forth row, where the values of 
is 21 as indicated in the respective rows. The abscissa in each small graph depicts 
which is the activation level of node 1, while the ordinate shows 
which is the activation level of node 2. The subscripts of K and R correspond to the numbers in the nodes in Figure 2. The light blue arrows demonstrate the dynamic flows and the series of red arrows indicate the courses of the limit cycles.
area with small values of
, and go through the neighbor points of the origin
.
It is found that all of the limit cycles are counterclockwise. The limit cycles arise in the case of
, implying that the inactivation reaction is more dominant than the activation reaction at node 1, while the activation reaction is more dominant than the inactivation reaction at node 2. As for the network D, node 1 has a positive auto-regulation and a negative regulation from node 2, while node 2 has a positive regulation from node 1. Therefore, if the system is operated around
, the value of 
would decrease under the condition of
; that is, the state would move left in 
-plane. When the value of 
becomes small enough, then the value of 
is getting lower since the activating power of 
to 
is getting weak; that is, the state would move down along with left edge of the 
-plane. The value of 
becomes small enough, and then the value of 
would be getting higher since the inactivating power of 
to 
is getting weak; that is, the state would move right along with bottom edge of the 
-plane. When the value of 
becomes high enough, the value of 
is getting higher since the activating power of 
to 
is retrieved; that is, the state would move up, and return to the starting point of the state. Subsequently, the next cycle would start again. This might be the mechanism for yielding the limit cycles.
3. Discussion
The characteristics of the emergence of stable equilibrium points are analyzed quantitatively by the emergence ratio and the sensitivity of equilibria which are newly proposed and defined in this study. These quantities seem to successfully detect the effects of the architectures and the values of parameters on the characteristics.
Comparison of the emergence ratios of bi-stable state for the regulatory networks as shown in Figure 2 suggests that the networks with high ratios have either the mutual positive or negative feedbacks. The auto-regulation seems to further affect the emergence of multi-stability. The effects of the mutual regulations and the auto regulations could be summarized as in Table 1; that is, positive mutual regulations or negative mutual regulations are likely to raise the emergence ratio of multi-stable state, while positive and negative mutual regulations tend to make the emergence ratio lower. With respect to the auto regulations, containment of node with both of positive auto regulation and negative regulation from
Table 1. Effects of network structure on emergence of multi-stable state.
The partial network structures in the upper row make the emergence ratio of multi-stable state higher, while those in the bottom row work reversely.
the other node could boost multi-stable systems, while a network containing node with both of negative auto regulation and positive regulation from the other node curtail the multi-stable systems.
As a common feature for the regulatory networks examined, smaller normalized Michaelis constant L yields higher emergence ratio of multi-stability or oscillation, implying that the condition of the higher saturation levels induces stronger nonlinearity. In the parameter spaces multi-stability arises in the region where 
is small in the case that the node is regulated positively and 
is large in the case that the node is regulated negatively, suggesting that the stronger regulation shifts the systems toward multi-stability. Multi-stable state is observed to emerge very robustly on the regulatory network J which undergoes mutual negative feedbacks and positive auto regulation on both of two nodes. It has been suggested that this robust reaction system works as the sequential Bayesian filter to reduce the noise in cells [16] [17] .
It is difficult to visualize and analyze the number of the stable equilibrium points and the values of the points, since high dimensional representation is required due to the existence of plural stable equilibrium points in two-dimen- sional space such as 
-plane at each point in the parameter space such as 
-plane. The sensitivity of equilibria is introduced to resolve this difficulty in this study. At first, the sensitivity is utilized to divide the parameter space to the robust area and high sensitive area, then the number of the stable equilibrium points and the values of the points are analyzed in the robust areas. It is revealed that the variations of these points are scarce and sorted in the robust areas as shown in the graphs in the bottom row in Figure 4.
Furthermore, the emergence of oscillations are analyzed to elucidate that the emergence of the oscillations are rare from the viewpoints of the regulatory structures and the values of parameters comparing to the high emergence of multi-stable states, such as 100% for the network J at the small values of L.
It is suggested that the method proposed in this study utilizing the emergence ratio and the sensitivity of equilibria are useful for this kind of analysis. On the other hand, it is unclear if these results are available to the higher order networks such as three-node or four-node regulatory networks due to the nonlinearity of the systems. Therefore, the similar analysis for the higher order networks are undergoing in our laboratory, facing the difficulty for the high dimension to visualize. It is also required to invent the new way to visualize and analyze the high dimensional dynamics.
4. Method
4.1. Range of Parameter Space for the Analysis
The analysis is performed with variation of the parameter values in appropriate range to cover the assumed values for reactions of MAPK cascade described in other studies [18] [19] [20] [21] [22] . From physiological point of view, the parameter set serves as surrogates of varying cellular activities across different cell types and cellular environments. We assume that the value of normalized Michaelis constant 
and 
in Equation (5) is common for all nodes to characterize the essence of the regulatory networks and to reduce the computational costs, which is denoted by L. The value of L is changed over the discrete values of 
(11 different values). 
is set to be independent values for each node, and has 11 different values as same as L. Therefore, the total number of parameter combinations of 
is 121 (i.e., 112).
4.2. Quantification for the Characteristics of Stability
Stability is assessed by the standard stability theory [23] . At first, a set of algebraic equations derived by setting the right-hand side of Equation (4) to be zero are solved to obtain the equilibrium points of the system. Then, the eigenvalues at those points are calculated for the Jacobian matrix of the set of algebraic equations. If the real parts of all eigenvalues are negative, the point is thought to be the stable equilibrium point. If more than two stable equilibrium points exist, then the system is multi-stable. We define emergence ratio of multi-stability as the percentage of the total number of combinations for the parameter (
) values yielding the multi-stability to the total number of examined combinations for parameter values, which is used to evaluate the characteristics of emergence of multi-stability quantitatively.
Furthermore, the sensitivity of equilibria (or equilibrium) is defined and utilized to quantify the effect of the change of parameter values on a set of stable equilibrium points. That is, the sensitivity denotes the change of numbers of the equilibrium points and how much the values of equilibria move when the values of parameters are changed. At first, we define the distance between two sets of points in two dimensional Euclid space as:
(6)
(7)
The defined distance 
is the longest Euclid distance among the shortest Euclid distances between a point in one set and a point in the other set. It should be noted that this distance is the metric since it fulfills the axioms for distances. Then, sensitivity is defined as
(8)
where 
is a set of the stable equilibrium points at 
and 
in the parameter space. Namely, the sensitivity is the mean value of distances between a set of the stable equilibrium points and a set of the stable equilibrium points at Neumann neighborhood. The system with low sensitivity is robust to the change of parameter values, while the high sensitivity might imply that the stability characteristics of the system could be regulated by the parameters.
Cite this paper
Sueyoshi, C. and Naka, T. (2017) Stability Analysis for the Cellular Signaling Systems Composed of Two Phosphoryltion-Dephosphorylation Cyclic Re-actions. Computational Molecular Bioscience, 7, 33-45. https://doi.org/10.4236/cmb.2017.73003
References
- 1. Ferrell, J.E. (1998) How Regulated Protein Translocation Can Produce Switch-Like Responses. Trends in Biochemical Sciences, 23, 461-465.
https://doi.org/10.1016/S0968-0004(98)01316-4 - 2. Jeschke, M., Baumgärtner, S. and Legewie, S. (2013) Determinants of Cell-to-Cell Variability in Protein Kinase Signaling. PLoS Computational Biology, 9, e1003357.
https://doi.org/10.1371/journal.pcbi.1003357 - 3. Kholodenko, B.N. (2006) Cell-Signalling Dynamics in Time and Space. Nature Reviews Molecular Cell Biology, 7, 165-176.
https://doi.org/10.1038/nrm1838 - 4. Mai, Z. and Liu, H. (2013) Random Parameter Sampling of a Generic Three-Tier MAPK Cascade Model Reveals Major Factors Affecting Its Versatile Dynamics. PLoS ONE, 8, e54441.
https://doi.org/10.1371/journal.pone.0054441 - 5. Qiao, L., Nachbar, R.B., Kevrekidis, I.G. and Shvartsman, S.Y. (2007) Bistability and Oscillations in the Huang-Ferrell Model of MAPK Signaling. PLoS Computational Biology, 3, e184.
https://doi.org/10.1371/journal.pcbi.0030184 - 6. Volinsky, N. and Kholodenko, B.N. (2013) Complexity of Receptor Tyrosine Kinase Signal Processing. Cold Spring Harbor Perspectives in Biology, 5, a009043.
https://doi.org/10.1101/cshperspect.a009043 - 7. Byrne, K.M., Monsefi, N., Dawson, J.C., Degasperi, A., Bukowski-Wills, J.C., Volinsky, N. and Kida, K. (2016) Bistability in the Rac1, PAK and RhoA Signaling Network Drives Actin Cytoskeleton Dynamics and Cell Motility Switches. Cell Systems, 2, 38-48.
https://doi.org/10.1016/j.cels.2016.01.003 - 8. Kuwahara, H. and Gao, X. (2013) Stochastic Effects as a Force to Increase the Complexity of Signaling Networks. Scientific Reports, 3, 2297.
https://doi.org/10.1038/srep02297 - 9. Ma, W., Trusina, A., El-Samad, H., Lim, W.A. and Tang, C. (2009) Defining Network Topologies that Can Achieve Biochemical Adaptation. Cell, 138, 760-773.
https://doi.org/10.1016/j.cell.2009.06.013 - 10. Mobashir, M., Madhusudhan, T., Isermann, B., Beyer, T. and Schraven, B. (2014) Negative Interactions and Feedback Regulations Are Required for Transient Cellular Response. Scientific Reports, 4, 3718.
https://doi.org/10.1038/srep03718 - 11. Ramakrishnan, N. and Bhalla, U.S. (2008) Memory Switches in Chemical Reaction Space. PLoS Computational Biology, 4, e1000122.
https://doi.org/10.1371/journal.pcbi.1000122 - 12. Shah, N.A. and Sarkar, C.A. (2011) Robust Network Topologies for Generating Switch-Like Cellular Responses. PLoS Computational Biology, 7, e1002085.
https://doi.org/10.1371/journal.pcbi.1002085 - 13. Tsai, T.Y.C., Choi, Y.S., Ma, W., Pomerening, J.R., Tang, C. and Ferrell, J.E. (2008) Robust, Tunable Biological Oscillations from Interlinked Positive and Negative Feedback Loops. Science, 321, 126-129.
https://doi.org/10.1126/science.1156951 - 14. Yao, G., Tan, C., West, M., Nevins, J.R. and You, L. (2011) Origin of Bistability Underlying Mammalian Cell Cycle Entry. Molecular Systems Biology, 7, 485.
https://doi.org/10.1038/msb.2011.19 - 15. Adler, M., Szekely, P., Mayo, A. and Alon, U. (2017) Optimal Regulatory Circuit Topologies for Fold-Change Detection. Cell Systems, 4, 171-181.
https://doi.org/10.1016/j.cels.2016.12.009 - 16. Kobayashi, T.J. (2010) Implementation of Dynamic Bayesian Decision Making by Intracellular Kinetics. Physical Review Letters, 104, Article ID: 228104.
https://doi.org/10.1103/PhysRevLett.104.228104 - 17. Kobayashi, T.J. and Kamimura, A. (2011) Dynamics of Intracellular Information Decoding. Physical Biology, 8, Article ID: 055007.
https://doi.org/10.1088/1478-3975/8/5/055007 - 18. Huang, C.Y. and Ferrell, J.E. (1996) Ultrasensitivity in the Mitogen-Activated Protein Kinase Cascade. Proceedings of the National Academy of Sciences, 93, 10078-10083.
https://doi.org/10.1073/pnas.93.19.10078 - 19. Brightman, F.A. and Fell, D.A. (2000) Differential Feedback Regulation of the MAPK Cascade Underlies the Quantitative Differences in EGF and NGF Signalling in PC12 Cells. FEBS Letters, 482, 169-174.
https://doi.org/10.1016/S0014-5793(00)02037-8 - 20. Levchenko, A., Bruck, J. and Sternberg, P.W. (2000) Scaffold Proteins May Biphasically Affect the Levels of Mitogen-Activated Protein Kinase Signaling and Reduce Its Threshold Properties. Proceedings of the National Academy of Sciences, 97, 5818-5823.
https://doi.org/10.1073/pnas.97.11.5818 - 21. Schoeberl, B., Eichler-Jonsson, C., Gilles, E.D. and Müller, G. (2002) Computational Modeling of the Dynamics of the MAP Kinase Cascade Activated by Surface and Internalized EGF Receptors. Nature Biotechnology, 20, 370-375.
https://doi.org/10.1038/nbt0402-370 - 22. Hatakeyama, M., Kimura, S., Takashi, N.A.K.A., Kawasaki, T., Yumoto, N., Ichikawa, M. and Yokoyama, S. (2003) A Computational Model on the Modulation of Mitogen-Activated Protein Kinase (MAPK) and Akt Pathways in Heregulin-Induced ErbB Signalling. Biochemical Journal, 373, 451-463.
https://doi.org/10.1042/bj20021824 - 23. Heinrich, R. and Schuster, S. (2012) The Regulation of Cellular Systems. Springer, New York.