Computational Molecular Bioscience
Vol.4 No.1(2014), Article ID:43789,24 pages DOI:10.4236/cmb.2014.41001
Application of Hartree-Fock Method for Modeling of Bioactive Molecules Using SAR and QSPR
Cleydson B. R. Santos1,2,3*, Cleison C. Lobato1, Francinaldo S. Braga1, Sílvia S. S. Morais4, Cesar F. Santos1, Caio P. Fernandes1,3, Davi S. B. Brasil1,5, Lorane I. S. Hage-Melim1, Williams J. C. Macêdo1,2, José C. T. Carvalho1,2,3
1Laboratory of Modeling and Computational Chemistry, Federal University of Amapá, Macapá, Brazil
2Postgraduate Program in Biotechnology and Biodiversity-Network BIONORTE, Campus Universitário Marco Zero, Macapá, Brazil
3Laboratory of Drug Research, School of Pharmaceutical Sciences, Federal University of Amapá, Macapá, Brazil
4Laboratory of Statistical and Computational Modeling, University of the State of Amapá, Macapá, Brazil
5Institute of Technology, Federal University of Pará, Belém, Brazil
Email: *breno@unifap.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 12 January 2014; revised 12 February 2014; accepted 20 February 2014
ABSTRACT
The central importance of quantum chemistry is to obtain solutions of the Schrödinger equation for the accurate determination of the properties of atomic and molecular systems that occurred from the calculation of wave functions accurate for many diatomic and polyatomic molecules, using Self Consistent Field method (SCF). The application of quantum chemical methods in the study and planning of bioactive compounds has become a common practice nowadays. From the point of view of planning it is important to note, when it comes to the use of molecular modeling, a collective term that refers to methods and theoretical modeling and computational techniques to mimic the behavior of molecules, not intend to reach a bioactive molecule simply through the use of computer programs. The choice of method for energy minimization depends on factors related to the size of the molecule, parameters of availability, stored data and computational resources. Molecular models generated by the computer are the result of mathematical equations that estimate the positions and properties of the electrons and nuclei, the calculations exploit experimentally, the characteristics of a structure, providing a new perspective on the molecule. In this work we show that studies of Highest Occupied Molecular Orbital Energy (HOMO), Low Unoccupied Molecular Orbital Energy (LUMO) and Map of molecular electrostatic potential (MEP) using HatreeFock method with different basis sets (HF/3-21G*, HF/3-21G**, HF/6-31G, HF/6-31G*, HF/ 6-31G** and HF/6-311G), that are of great importance in modern chemistry, biochemistry, molecular biology, and other fields of knowledge of health sciences. In order to obtain a significant correlation, it is essential that the descriptors are used appropriately. Thus, the quantum chemical calculations are an attractive source of new molecular descriptors that can, in principle, express all the geometrical and electronic properties of molecules and their interactions with biological receptor.
Keywords:Molecular Modeling; Meps Maps; Orbital Frontier; Quantum Chemical Methods

1. Introduction
Brazil has the largest genetic diversity in plant species in the world, however it is estimated that less than 10% were evaluated as their biological characteristics and less than 5% were submitted the detailed phytochemical studies. Despite a recent increase in research in this area, plants still constitute a source relatively underused and potentially very valuable for discovery of new biologically active substances [1] [2] . The bioactive compounds present in the vegetable kingdom have important functions and biological actions and may be considered as promoters of human health. We have already recognized the association between intake of fruits and vegetables and decreased risk of development various disorder chronic degenerative, such as cancer, inflammation, cardiovascular disease, cataracts, macular degeneration and other being carotenoids and phenolic compounds, some of the groups of bioactive compounds to which are attributed such actions. The seeds and extracts of annatto (Bixa orellana L.) are used as colorants in food, pharmaceutical and cosmetic industries due to the predominant presence of the carotenoid bixin [3] . The efficiency of biological activity of bioactive compounds of vegetable origin depends on their structure and concentration. In turn, the amount of these substances in vegetables is largely influenced by genetic factors and environmental conditions, in addition of the degree of maturation and plant variety, among other things. It is known also that the biological capacity is influenced by the substrate used in the assay, by the solvent and by extraction technique used, as well as the binomial time-temperature. Regarding the organic solvents, methanol, by managing to extract high amount of bioactive compounds, it has been touted as the most effective [4] -[7] .
The Montrichardia linifera (Arruda) Schott, Araceae family, popularly known as “aninga”, is an aquatic macrophyte that forms large clonal populations along the rivers and streams of the Amazon. Those bordering consider this poisonous plant because its sap causes skin burns and eye contact can cause blindness [8] . However, paradoxically, it is widely used in traditional Amazonian medicine, mainly due to the healing properties of sap and of the juice of this plant, which has already been mentioned in the literature since the nineteenth century for the treatment of wounds and ulcers [9] -[12] , leading to the hypothesis that this species may contain biologically active substances. However, very little is known about their chemical composition and biological activities that eventually may be useful also against human infections caused by parasites, which are serious problems in tropical and subtropical in developing countries, despite the discovery of new anti-protozoal drugs [13] . Between antimalarial compounds isolated from plants, artemisinin is one of the most important discoveries nowadays [14] -[16] . Artemisinin (or Qinghaosu, QHS, Figure 1) represents the most relevant advance in the treatment of malarial disease for the last 20 years [17] . Artemisinin is a sesquiterpene lactone with an endoperoxide group, which has been used in traditional Chinese medicine for many centuries as a natural product for fever and malarial treatment. This drug was isolated by Chinese chemists in the early 1970s from the ancient Artemisia annua L. Nowadays, artemisinin and derivatives are widely used around the world because of their potent antimalarial activity, fast action, and low toxicity. As a result, artemisinin and its derivatives have become recognized as a new generation of antimalarial drugs [18] .
Pinheiro, Ferreira and Romero (2001) techniques combined quantum chemical (Hartree-Fock 3-21G) and multivariate analyzes methods (PCA, HCA, KNN and SIMCA) to study and propose diidroartemisinin derivatives. Through the technique PCA and HCA, seven (7) descriptors that were responsible for the classification of compounds into two distinct classes were selected, and with construction of qualitative models KNN and SIMCA
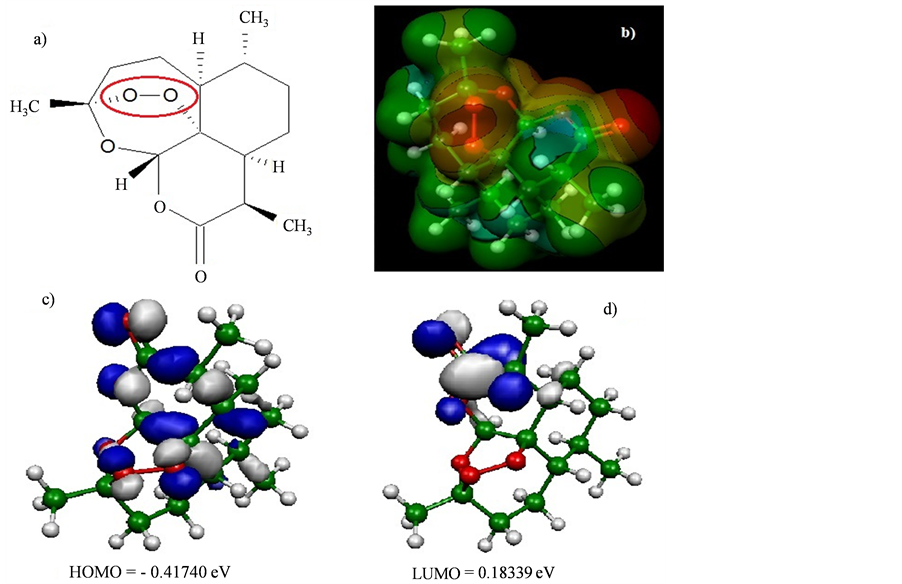
Figure 1. (a) The artemisinin structure and the region essential for expression of the biological activity (pharmacophore) was visualized using ChemSketch 12.00 program [23] . (b) Map of molecular electrostatic potential (MEP). ((c) and (d)) Orbital’s energy Homo and Lumo. The MEP, Homo and Lumo were visualized and calculated using HartreeFock (HF) method and HF/6-31G** basis set by the Molekel program [24] .
two (2) compounds of a set of twelve (12) test predicted as of high activity were proposed [19] . Artemisinin derivatives with antimalarial activity against Plasmodium falciparum, which is resistant to mefloquine, were studied using quantum chemical methods (HF/6-31G*) and the partial least-squares (PLS) method. Three main components explained 89.55% of the total variance, with Q2 = 0.83 and R2 = 0.92. From a set of 10 proposed artemisinin derivatives (artemisinin derivatives with unknown antimalarial activity against Plasmodium falciparum), a novel compound was produced with superior antimalarial activity compared with the compounds previously described in the literature [20] . Cardoso et al. (2008) studied artemisinin and some of its derivatives with activity against D-6 strains of Plasmodium falciparum using the HF/3-21G method. To verify the reliability of the geometry obtained, Cardoso et al. compared the structural parameters of the artemisinin trioxane ring with theoretical and experimental values from the literature. MEP was used in an attempt to identify key features of the compounds that are necessary for their activities, and they use those to propose new artemisinin derivatives [21] . There is however, the need for discovery of new antimalarial drugs using techniques of quantum chemistry which has been extensively used in the pharmaceutical industry, where predicting the probable activity of a drug from molecular orbital calculations is much less expensive than manufacturing it in order to perform expensive tests [22] .
2. The Importance and Application of the Methods of Quantum Chemistry to Molecular Modeling
The central importance of quantum chemistry is to obtain solutions of the Schrödinger equation for the accurate determination of the properties of atomic and molecular systems. Within the area of physical chemistry, quantum chemistry is used to calculate various thermodynamic properties such as entropy, heat capacity of gases, for the interpretation of molecular spectra, calculations of bond length, bond angles, dipole moment and the understanding of intermolecular forces. In organic quantum chemistry can estimate the stability of molecules, calculate the properties of intermediate reactions, reproduce the aromaticity of organic compound and simulate spectra of nuclear magnetic resonance (NMR). In analytical chemistry is used for the interpretation of intensities of the spectral lines. In the area of inorganic chemistry is used for the ligand field theory, where predictions are made, and properties justify complex ions of transition metals. In Biochemistry of quantum chemistry calculations are used to study the conformation of biological molecules such as enzyme-substrate binding and solvation of organic molecules [25] -[28] .
The application of quantum chemical methods in the study and planning of bioactive compounds has become a common practice nowadays. From the point of view of planning, it is important to note that, when speaking of the use of molecular modeling (a collective term that refers to theoretical methods and computational techniques to model or mimic the behavior of molecules), it is not intended to reach a bioactive molecule simply through the use of computer programs. The development process of these molecules due to their complexity, necessarily involves multidisciplinary approach, which employs a large set of computational methods of systematic way form facilitate and optimize the development process of bioactive compounds, on a constant exchange of information with groups of chemical synthesis and evaluation of the activity of these compounds. These computational methods can be used as tools of rational design of bioactive compounds, so called because it is guided by a rational hypothesis about the mechanism of action of these compounds. The action of bioactive molecules is a very complex phenomenon, but one of the paradigms of medicinal chemistry is that these molecules are related to their effects or interactions to chemical reactions with macromolecular structures present in living systems, proteins, in its large majority. Cases these proteins are cell receptors, bioactive molecules are classified as receptor agonists or antagonists, in the case of enzymes, these molecules act as enzyme inhibitors [29] [30] .
The Origin of Quantum Chemistry Methods
The history and debates related to the so called “semiempirical method” of London-Eyring-Polanyi are reported on a fascinating work of Nye [31] . The approach of Eyring and Polanyi, aiming to merge theory with experimental results to construct potential energy surfaces, showed that it is possible to gain insights into the mechanisms of adiabatic reactions, leading to important concepts related to the dynamics of chemical reactions, such as transition state and activated complex. Already at that time, there were debates comparing the approaches based on first principles with the semiempirical. In 1933 James and Coolidge [32] published an ab initio calculation when obtained the binding energy of H2 molecule with an accuracy of 98%. This calculation took a year to be done, but its success increased confidence of authors that then criticized the semiempirical method as a “happy cancellation of errors” that occurs for not taking into account “terms of considerable importance” [32] . This expression “cancellation of errors” remains to this day in the imagination of researchers, although it is not possible to identify precisely that are these errors, and mainly, how and why they if would cancel. Polanyi in 1937 counter-argued: “Personally, I do not attach importance to an exact agreement between theory and experiment at this stage, but I believe that the theory [referring to the semiempirical method] can claim to provide a reasonable description of the mechanism of reactions chemical that would otherwise remain obscured” [33] .
In 1941 Hirschfelder presented the calculation of at least one hundred activation energies for several reactions using the method of London-Eyring-Polanyi, showing that only in some cases the values did not agree with the experimental, with an error of 10 kcal/mol [34] . Hirschfelder defended the semiempirical method as “a method sufficiently flexible so that it could be made consistent with any set of chemical facts, maintaining consistent with the basic principles of quantum mechanics”. According to Nye [31] , in this statement Hirschfelder has correctly identified that an ad hoc character is inherent to semi-empirical approaches. This ad hoc character involves risk, since it may well be possible to force an agreement between the semi-empirical and experimental model, even if the model is based on an erroneous theory. Such risk is even greater if the model is used for extrapolation. The final triumph of the first principles approach to the reaction H + H2 ® H2 + H, occur only came in 2003 when Mielke and colleagues [35] presented a new constants of experimental and theoretical speeds. The theoretical calculations were obtained using quantum dynamics in an exact adiabatic potential surface including Born-Oppenheimer corrections. The experiment and theory now agree in the range of 167 K to 2112 K, within experimental error, causing the problem can be solved now.
The “semiempirical” expression was first used in theoretical chemistry in 1931 by Michael Polanyi (1891- 1976) and Henry Eyring (1901-1981) [36] [37] in their attempt to combine thermodynamics, chemical kinetics, quantum mechanics and the theory of binding electrons valence. In these 82 years, semiempirical method of London-Eyring-Polanyi to construct potential energy surfaces, provided a work tool useful to get insights about how the physical and chemical processes occur, and to motivate the development of new techniques and experiments to study the temporary combination of atoms called transition state as in the works of Ahmed Zewail. The novelty of the visual maps of potential energy surfaces and the language of potential wells and barriers of activation has also become an important pedagogical tool for chemistry. In contrast, first-principles calculations of quantum dynamics, with equivalent accuracy to that of Mielke and colleagues [35] , remain prohibitive, almost impossible to be performed for the vast majority of chemical reactions of practical interest. Undoubtedly: the ab initio methods, based entirely on first principles eventually prevail. However, if the reaction of the hydrogen atom with a hydrogen molecule could be regarded as definitely settled 10 years ago, what about all the other chemical and biochemical reactions? [38]
3. Hartree-Fock Equations
A development of great importance in quantum chemistry occurred from calculation functions accurate wave diatomic and for many polyatomic molecules, by the method of self-consistent field developed by Douglas Hartree [39] . In his theory Hartree considered the wave function as being formed by an antisymmetric linear combination of products of spin-orbitals. Then the wave function Hartree-Fock for atoms or molecules obeying the Pauli exclusion principle, should be written as a product antisimetrizado spin-orbitals, called Slater determinant, that in the formula restricted and normalized to a system of closed layers containing 2m electrons, is given by:
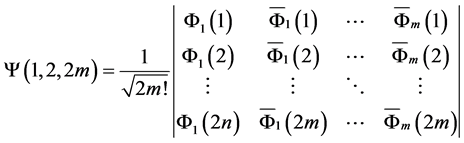 (1)
(1)
in which each spin-orbital 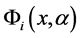 is a product of a spatial function
is a product of a spatial function 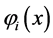 and a spin function
and a spin function  or
or 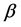
 (2)
(2)
The functions of an electron 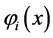 are known as “orbitals”, a term proposed by Mulliken [40] , which is the quantum mechanical analogue of the classical orbit [41] . It is considered that the orbitals are orthonormal
are known as “orbitals”, a term proposed by Mulliken [40] , which is the quantum mechanical analogue of the classical orbit [41] . It is considered that the orbitals are orthonormal
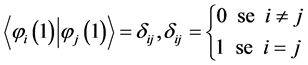 (3)
(3)
All elements forming a given column of Slater determinant involve the same spin-orbital already all elements in the same row involve the same electrons. When the configuration of an atom or molecule layer is closed this is represented by a single determinant, unlike a configuration layer to open, since in this case it is used a sum of Slater determinant. The analysis made the following refers the systems configurations closed layer. Open layer settings will not be discussed here, viewed the complexity of the formulas. Aiming to show a simple format for the expressions, it is used the system of atomic units in the equations.
The expression refers to the total electronic energy Hartree-Fock E for a system of electrons n nuclei in fundamental state is given by the theorem of the variational method.
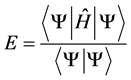 (4)
(4)
where  comes to be wave function in the form of Slater determinant and
comes to be wave function in the form of Slater determinant and 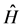 is the Hamiltonian operator without considering the coordinates spin system and non-relativistic. In the case of molecules that in our case the operator
is the Hamiltonian operator without considering the coordinates spin system and non-relativistic. In the case of molecules that in our case the operator 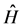 is the Hamiltonian purely electronic which is obtained after the separation of Born-Oppernheimer [42] that written in atomic units has the form:
is the Hamiltonian purely electronic which is obtained after the separation of Born-Oppernheimer [42] that written in atomic units has the form:
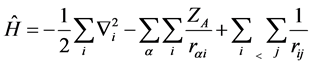 (5)
(5)
The first term in Equation (5) is the operator for the kinetic energy of the electrons, the second term comes to be potential energy of attraction between electrons and nuclei, and the last term refers to the potential energy of repulsion between the electrons, 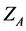 is the charge of the nucleus A,
is the charge of the nucleus A, 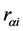 is the distance of the electron i the nucleus a and
is the distance of the electron i the nucleus a and 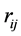 is the distance of the electron i to the electron j.
is the distance of the electron i to the electron j.
The operator  can be separated into two other operators
can be separated into two other operators
 (6)
(6)
The operator  is relative to the kinetic energy of the electrons and the potential energy of interaction of the electrons with the nuclei:
is relative to the kinetic energy of the electrons and the potential energy of interaction of the electrons with the nuclei:
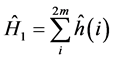 (7)
(7)
The operator  is the corresponding Hamiltonian to the motion of an electron in the field generated by the nuclei only
is the corresponding Hamiltonian to the motion of an electron in the field generated by the nuclei only
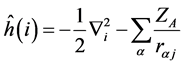 (8)
(8)
The operator 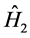 is associated with the interelectronic repulsion
is associated with the interelectronic repulsion
 (9)
(9)
Utilizing the wave function (1) and the Hamiltonian (5) in the expression for the energy functional (4), has been as a result the expression for the total electronic energy of a system represented by a wave function in the form of Slater determinant.
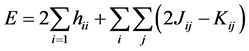 (10)
(10)
This relationship has reduced the integration of many electrons the set of three dimensional integrals (hij) and six (Jij) and (Kij), written of following form:
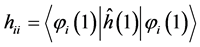 (11)
(11)
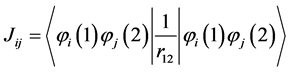 (12)
(12)
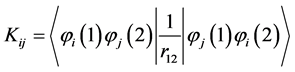 (13)
(13)
The integral of an electron 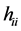 represents the sum of the kinetic energy of an electron in the orbital
represents the sum of the kinetic energy of an electron in the orbital 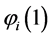 and its potential integral due to the action of the nuclei. The Coulomb integrals
and its potential integral due to the action of the nuclei. The Coulomb integrals 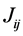 and of exchange
and of exchange 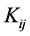 are associated to interaction between an electron in the orbital
are associated to interaction between an electron in the orbital 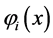 and another in the orbital
and another in the orbital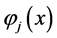 . In classical mechanics the integral Coulomb is the interaction energy between two distributions of charges, already integral exchange does not have analogue in classical mechanics, their presence arises due to anti-symmetry of the wave function [41] . Varying E in Equation (4) for each orbital and making
. In classical mechanics the integral Coulomb is the interaction energy between two distributions of charges, already integral exchange does not have analogue in classical mechanics, their presence arises due to anti-symmetry of the wave function [41] . Varying E in Equation (4) for each orbital and making 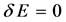 while keeping orthonormality of the wave function arrives at the 1-electron equations that define the Hartree-Fock method
while keeping orthonormality of the wave function arrives at the 1-electron equations that define the Hartree-Fock method
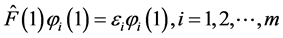 (14)
(14)
where Fock operator 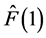 is given by
is given by
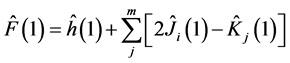 (15)
(15)
where 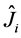 and
and 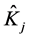 are respectively operators of Coulomb and exchange
are respectively operators of Coulomb and exchange
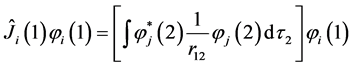 (16)
(16)
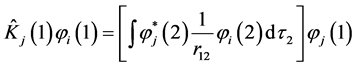 (17)
(17)
The Hartree-Fock equations are solved in general by an interactive procedure (SCF). At the end of the procedure, 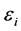 are the eigenvalues monoeletrônicos HF system. Each
are the eigenvalues monoeletrônicos HF system. Each 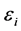 is often called orbital energy and is interpreted as being the energy of an electron in the orbital
is often called orbital energy and is interpreted as being the energy of an electron in the orbital , resulting from its kinetic energy, energy of attraction with the nuclei and their energy exchange and repulsion due to all other electrons in their charge density
, resulting from its kinetic energy, energy of attraction with the nuclei and their energy exchange and repulsion due to all other electrons in their charge density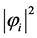 .
.
The Equation (14) provides
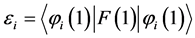 (18)
(18)
Substituting Equation (15) in (18) we can relate the orbital energies with the integrals (11), (12) and (13).
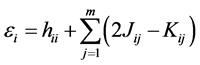 (19)
(19)
It may be also find the total electron energy E from the orbital energies. But this total energy is not simply equal the sum of the energies of an electron. This fact is due to the sum of the energies of an electron including twice each electron-electron interaction, i.e., repulsion between electrons 1 and 2 contributes to the energy of an electron associated with both electrons. Thus it follows that the second term in the equation below corrects this problem
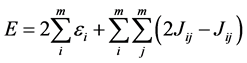 (20)
(20)
Thus substituting (19) in (20) have
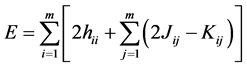 (21)
(21)
which equals
 (22)
(22)
with 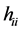 being the same Equation (11).
being the same Equation (11).
3.1. Hartree-Fock-Roothaan Method
The problem of solving the Hartree-Fock equations for atoms and molecules is due to the fact of absence of central symmetry. Therefore it is necessary to use approximations for the best orbital. Thus for systems containing many electrons, an approximated way of revolver the Hartree-Fock equations consists of expand the orbital Hartree-Fock 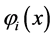 on a linear combination of K basis functions
on a linear combination of K basis functions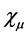 , in accordance proposed by Roothaan [43] , and this method denominated of Hartree-Fock-Roothaan (HFR) or also Molecular-Orbital Linear Combination Atomic Orbitals (LCAO-MO). Thus the orbital can be expanded in a linear combination as follows.
, in accordance proposed by Roothaan [43] , and this method denominated of Hartree-Fock-Roothaan (HFR) or also Molecular-Orbital Linear Combination Atomic Orbitals (LCAO-MO). Thus the orbital can be expanded in a linear combination as follows.
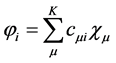 (23)
(23)
where the 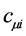 are the coefficient of expansion, which will be treated as variational parameters and basis functions
are the coefficient of expansion, which will be treated as variational parameters and basis functions 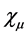 are Slater type atomic orbitals or Gaussian type. To accurately represent the orbitals, functions should form a complete set. However, this requires an infinite number of such functions. What you should use is actually a finite number of basis functions. Orbitals should obey the orthonormality condition. Otherwise you can make a linear transformation thereby making them orthonormal
are Slater type atomic orbitals or Gaussian type. To accurately represent the orbitals, functions should form a complete set. However, this requires an infinite number of such functions. What you should use is actually a finite number of basis functions. Orbitals should obey the orthonormality condition. Otherwise you can make a linear transformation thereby making them orthonormal
 (24)
(24)
where 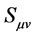 is the overlap integral
is the overlap integral
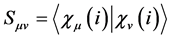 (25)
(25)
For the molecules  are molecular orbitals and
are molecular orbitals and 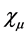 are the atomic orbitals. Thus there is a significant improvement in computational calculations when the orbital functions are expanded in terms of a finite set of basis functions. The integro-differential equations are then transformed into algebraic equations for the expansion coefficients [41] . The total electronic energy is obtained when Equation (23) is replaced in (21).
are the atomic orbitals. Thus there is a significant improvement in computational calculations when the orbital functions are expanded in terms of a finite set of basis functions. The integro-differential equations are then transformed into algebraic equations for the expansion coefficients [41] . The total electronic energy is obtained when Equation (23) is replaced in (21).
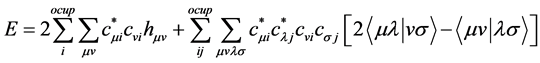 (26)
(26)
where
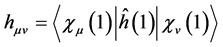 (27)
(27)
with 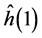 given by Equation (8) by replacing i by 1.
given by Equation (8) by replacing i by 1.
The integrals 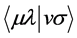 and
and 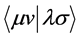 are integral interaction two electrons are represented by
are integral interaction two electrons are represented by
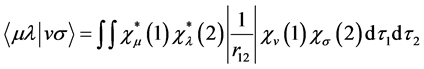 (28)
(28)
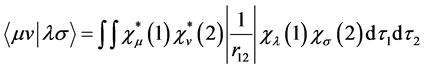 (29)
(29)
The best coefficients 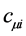 are determined by varying the electron energy given by Equation (26) with respect to them, obeying the condition of orthonormality. Thus we arrive at the equations of Hartree-Fock-Roothaan
are determined by varying the electron energy given by Equation (26) with respect to them, obeying the condition of orthonormality. Thus we arrive at the equations of Hartree-Fock-Roothaan
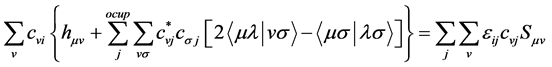 (30)
(30)
where the operator Fock defined as
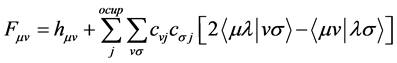 (31)
(31)
We can replace the Equation (31) in (30) and thus obtain the equations of Hartree-Fock-Roothaan the following notation
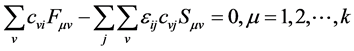 (32)
(32)
Applying a unitary transform on Equation (32) to diagonalize the matrix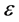 , has been
, has been
 (33)
(33)
Equation (33) can be written in matrix form in this way has been
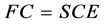 (34)
(34)
The equations of Hartree-Fock-Roothaan are resolved in the same way that the equations of Hartree-Fock, i.e., by an interactive process (SCF-MO-LCAO). Those obtained at the end of the procedure are the eigenvalues of HFR system.
3.2. Hartree-Fock Limit
In Hartree-Fock method, is used a electronic wave function composed only by a Slater determinant, thereby providing only approximate description of exact wave function because this can not be described by a single Slater determinant. The exact solution of the Schrödinger equation would not be obtained in case the spatial orbitals 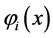 be expanded into a linear combination of basis functions
be expanded into a linear combination of basis functions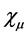 , although the larger and more complete is the set of those functions greater the degree of flexibility in expansion for spin-orbital and lowest expected value for energy. Larger bases sets decrease the HF energy up to a certain limit. This limit is the lowest that can be obtained from a wave function of a determinant and it is called of Hartree-Fock limit. Even so, as a variational method, this limit energy EHF will still be above the exact nonrelativistic energy
, although the larger and more complete is the set of those functions greater the degree of flexibility in expansion for spin-orbital and lowest expected value for energy. Larger bases sets decrease the HF energy up to a certain limit. This limit is the lowest that can be obtained from a wave function of a determinant and it is called of Hartree-Fock limit. Even so, as a variational method, this limit energy EHF will still be above the exact nonrelativistic energy 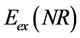 due to the energy of electron correlation Ecorr
due to the energy of electron correlation Ecorr
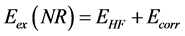 (35)
(35)
The SCF method is a valid approach, but generates errors in energy because it describes of approximate mode the interactions between the electrons. Should be also consider the instantaneous interactions between the electrons. The moves of the electrons are correlated with each other, i.e., there is a correlation in the different positions of the electron and must be taken into account.
The exact value of the energy E including electron correlation and relativistic effects Erel is given by:
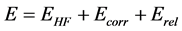 (36)
(36)
4. Application of Basis Sets Separate Valence Used in the Molecular Modeling
To perform atomic and molecular calculations, determines a basis set formed by mathematical functions. These bases consist of a linear combination of the wave functions of an electron in terms of a finite number of base functions, which contains a set of parameters to be optimized. The denomination of the base sets depends on various types of basis functions, of the number of those employed functions in the expansion of monoeletrônicas functions (orbital) and of characteristics of the parameters to be optimized. Thus it is of fundamental importance the careful choice these functions when you want to get accurate results. The main basis sets separate valence available in computational chemistry programs for performing calculations of molecular properties are presented below:
4.1. Slater Type Functions
The atomic systems containing only one electron, hydrogenic atoms, have as a solution of the Schrödinger nonrelativistic equation, a function of type
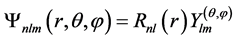 (37)
(37)
where n, l and m are the principal quantum numbers, orbital angular momentum and magnetic, 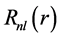 is the radial part and
is the radial part and  is the angular part denominated spherical harmonics. The radial part has the form
is the angular part denominated spherical harmonics. The radial part has the form
 (38)
(38)
where Nnl comes to be a normalization factor, Z is nuclear charge, r is radius, a is a constant and 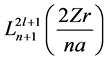
represents in a generic form a polynomial called associated Laguerre polynomial. The angular part is equal to
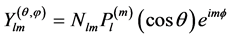 (39)
(39)
being Nlm a normalization factor and 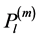 the associated Legendre polynomial.
the associated Legendre polynomial.
For more that hydrogenic orbitals are orthogonal they do not form a complete set of continuous functions. They have limited application because many of the required integrals in molecular orbital calculations are somewhat hard to calculated, especially when you have high values of the principal quantum number because of the complexity of the polynomial in r. Then Slater (1930) proposed a form analytical simpler for the radial function, then introducing functions such as Slater (Slater Type Functions-STFs) [42] .
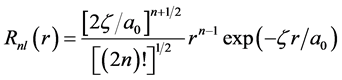 (40)
(40)
Since the orbital exponent is written as
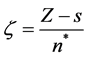 (41)
(41)
where s is a constant related to the shielding effect of the electrons of the internal layers of atoms and n* is an effective principal quantum number. Therefore the general shape of Slater type functions can be written as follows, which is similar to the equation.
 (42)
(42)
Slater evaluated through empirical rules to select of parameters s and n*, thereby aiming at a good approximation for the atomic orbitals best of this type. The values of  were determined by the variational method by Clementi (1963 and 1967) for neutral atoms to the ruthenium in their fundamental states, using for this the SCF method [44] [45] . The exponents
were determined by the variational method by Clementi (1963 and 1967) for neutral atoms to the ruthenium in their fundamental states, using for this the SCF method [44] [45] . The exponents 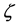 are positive numbers and adjustable in the methods of calculation. These exponents determine the size of the orbital, thereby large exponents characterize dense orbital and small exponents characterize diffuse orbitals.
are positive numbers and adjustable in the methods of calculation. These exponents determine the size of the orbital, thereby large exponents characterize dense orbital and small exponents characterize diffuse orbitals.
The so-called Slater type orbitals (STOs) are formed by the product of the angular part of Equation (39), by the product of the radial part of Equation (40). The STOs generate reasonable representations of atomic orbitals. However, as they replace the polynomial in r in the hydrogenic orbitals by a simple power r, do not have the proper number of radial nodes, just not well represent the internal part of an orbital.
One of the limitations is that they are not of mode some orthogonal, as much as it can be corrected using a set of STOs orthogonalized. In addition the use of these orbitals in molecular SCF calculations makes the integrals multicenter, that involve interactions between electrons, becomes somewhat difficult to be solved numerically, thereby increasing the computational time.
4.2. Minimum Base Sets
Minimum base sets or base “single-zeta” is set containing a single function to represent each occupied atomic orbital of different quantum numbers n and l of electron configuration. Thus, this set presents a reduced computational time to make these calculations, so can be used in calculations involving large molecules which are our case. In the calculations where a minimum base set is used are used in general Slater type orbitals. Due to the small size of the base, minimum base sets generate results only form qualitative of the properties. Nevertheless the calculations of the electronic structure were until around 1960 all performed in terms of minimum base. The first semiempirical methods more used were based in a set of minimum base STOs [46] [47] .
4.3. Gaussian Type Functions
4.3.1. Contracted Gaussian Functions
The use of STOs in electronic structure calculations generates computational problems due to the emergence of multicenter integrals, although these orbitals well describe the functional behavior of molecular orbitals. In order to simplify the calculation of multicenter integrals, Boys (1950) proposed for calculations involving molecules using Gaussian type functions (GTFs) [48]
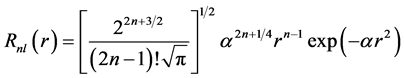 (43)
(43)
where n and l are the main quantum numbers and orbital angular momentum and 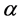 is the orbital exponent which is a variational parameter. The use of GTFs in calculations of electronic interaction integrals presents an enormous advantage, because the product two of these functions entries in different centers is equivalent to a single function centered on a new center [49] , thereby there is a reduction of multicenter integrals to integrals calculated in terms of functions centered on the same point.
is the orbital exponent which is a variational parameter. The use of GTFs in calculations of electronic interaction integrals presents an enormous advantage, because the product two of these functions entries in different centers is equivalent to a single function centered on a new center [49] , thereby there is a reduction of multicenter integrals to integrals calculated in terms of functions centered on the same point.
The functions of the type Gaussian have a poor behavior of atomic orbitals in relation to Slater type functions, the reason is that the GTFs do not have the “cusp” in the region near the nucleus. Thus the GTFs have a behavior different functional that seen for molecular orbitals, so it is necessary to use two (2) to five (5) GTFs to represent adequately each STO. As the number of electronic interaction integrals originated using of a basis set dimension m increases in the order of m4, fastest speed and simplify the calculations of the electronic interaction integrals in terms of GTFs compensates the large number of integrals to be calculated when comparing using STFs.
The solution of the equations of SCF method in the calculation HFR is also a process using an enormous computational time, it is also proportional to the fourth power of the number of base functions. However, the number of cycles of the interactive process SCF method increases with the number of coefficients to be optimized. Thus the use of GTFs contracted originated from linear combinations of Gaussian primitive is generally more adequate [47] [50] [51] .
The contracted basis functions can be chosen in order to resemble STOs, atomic orbitals HF or any other set of functions. A type of GTFs contracted is set STO-NG. This nomenclature comes being a set of GTFs contracted that describes a STF through N GTFs primitives used in contraction. Each STO is then approximated as a linear combination of N GTFs, in which the coefficients and exponents contracted are chosen so that the basis function approach is an STF. Thus the computational time decreases, but the results generated by the set of contracted GTFs are not good.
The STOs ns and np are approximated by their respective functions
 (44)
(44)
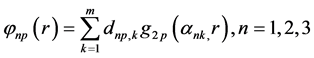 (45)
(45)
where 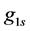 and
and 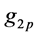 are GTFs,
are GTFs, 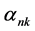 are gaussian exponents and
are gaussian exponents and  and
and 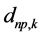 are coefficients of the expansion, where the last three parameters are determined by the least squares method [51] .
are coefficients of the expansion, where the last three parameters are determined by the least squares method [51] .
4.3.2. Basis Sets Separate Valence
In order to obtain better results, many studies have been made aimed at finding basis sets with this capability. In recent years, besides the basis sets previously described, other sets are being used in electronic structure calculations. Among these, there are basis sets separate valence [42] .
Basis sets separate valence are extended sets GTFs contracted, where the most usual are listed below: 4-31G, 3-21G, 6-31G e 6-311G. In such sets are used two functions for the valence orbitals and only one for the orbitals of the internal layer, may each of these functions is a linear combination or not primitive gaussian. The occurrence of this is due the internal layer contribute little to the chemical properties of interest. As the functions of the internal layers not duplicate it generates effects on total energy, however represents little it comes of dipole moments, ionization potentials of the valence, charge density, dissociation energy and other chemical properties. For example, the base 4-31G each atomic orbital of the internal layers is described by only one GTF contracted which is formed by the combination of four linear (4) GTFs primitive. For each atomic orbital of the valence shell there are two basic functions, being that of them is a GTF contracted from the linear combination of three (3) GTFs primitive, describing the internal part of valence orbital, since the other is a single GTF primitive, which describes the outer part of the valence orbital. Considering the first row atoms (Li to F) we have:
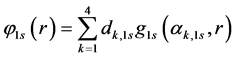 (46)
(46)
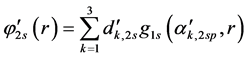 (47)
(47)
 (48)
(48)
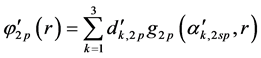 (49)
(49)
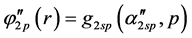 (50)
(50)
For the hydrogen atom, which has no internal layer, it has been:
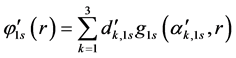 (51)
(51)
where the functions which appear with (') are internal functions while appearing with (“) are external functions. Similarly to the base structure previously described is the basis 6-31G. Only now each orbital of internal layers is represented by a GTF contracted originated from linear combination of six (6) GTFs primitive. In the case of the base 6-311G, includes a GTF primitive the set 6-31G to represent a new layer of the outer valence.
4.4. Polarization Function
All basis sets discussed so far have a peculiar characteristic, i.e., they comprise functions restricted to be centered in the nuclei. However, there is evidence showing that the atomic orbitals distort or polarize when they form a molecule. For this reason one should take into consideration the possibility of non-uniform displacement of electric charges outside the atomic nucleus, i.e. the polarization. Thus it is possible to obtain a better description of the changes as well as also deformations in the atomic orbitals within the molecule.
One way to consider such a polarization is introduced on the basis in question functions wherein the values of l (quantum number of the orbital angular momentum) larger than those of fundamental state of a given atom. In this type of functions gives the name of polarization functions. For the hydrogen atom of the description fundamental state uses only functions s. The functions p, d, ... centered on H, for molecular calculate, are considered as functions of polarization. Generally, with the inclusion of polarization functions in the molecular basis there is a higher possibility of obtaining better results for many of the properties of chemical interest, such as dissociation energy and dipole moments. In real terms, it is noted that it is not satisfactory to include polarization functions of symmetry d and f together with the basis sets s and p small, that is, the polarization functions should only be added when working with basis sets said saturated [52] .
Of the bases valence separate with polarization functions most commonly used in molecular calculations are the STO-3G*, 3-1G*, 6-31G*, 6-31G**, 6-311G* and 6-311G** [53] . The base 6-31G* and 6-31G** are formed by the inclusion of polarization functions to the base 6-31G, being that the base 6-31G* is constructed by adding a set of five (5) polarization functions of type GTFs of symmetry d to the base 6-31G, for each different atom of hydrogen and helium, already the basis 6-31G** is constructed by adding a set of three (3) polarization functions of type GTFs of symmetry p to the set 6-31G*, for each hydrogen atom.
4.5. Diffuse Functions
The use of valence basis set with polarization function in calculations involving anions does not generate good results, because the electron cloud of the anionic systems possess a tendency to expansion. Thus it is necessary to also add appropriate diffuse functions because they allow a greater occupation of space by the orbital region. The importance of diffuse functions in calculations of transition metals is due to the metal atoms present orbital type d and these have diffuse characteristics. So it becomes necessary adding diffuse functions to basis function associated to configuration of the neutral metal atom in order to obtain a better description of the metal complex. The great importance of diffuse functions is due to the fact that they better describe the farthest molecular orbital of the nuclei [54] .
5. Computational Chemistry Software for Calculating Molecular Properties
Several computational chemistry softwares make available calculations of molecular properties through semiempirical and Hatree-Fock methods. We can cite: MOPAC2002 [55] , VAMP [56] , MNDO97 [57] , Gaussian98 [58] , Spartan [59] , GAMESS [60] , Chem3D [61] , CAche [55] , HyperChem [62] , ZINDO [63] , GEOMOS [64] . Most of the great advances obtained in the research of semi-empirical methods were essentially incorporated on a series of programs entitled MOPAC [62] . MOPAC should be understood as an abbreviation of Molecular Orbital PACkage. Initiated in 1983, on group of Prof. M. Dewar, with the participation of Prof. J. J., P. Stewart, the MOPAC project currently has 30 years, and the main landmarks of this story are:
1) 1983: MOPAC ® Geometry optimization, vibrational analysis and transition states.
2) 1984: MOPAC 2 ® Solution of errors.
3) 1985: MOPAC 3 ® AM1 method, calculation of polymers and CI (Configuration interaction).
4) 1987: MOPAC 4 ® Solution of errors.
5) 1988: MOPAC 5 ® PM3 method and way of reaction.
6) 1989: MOPAC 6 ® Repair errors, calculation of electrostatic potential and extent of PM3 for 28 elements.
7) 1993: MOPAC 7/93 ® Model solvent, nonlinear optical properties and analysis of symmetry.
8) 1997: MOPAC 97 ® MNDO-d method 9) 1999: MOPAC2000 ® Dynamic memory allocation, large molecules, solids, transition metals, improving the search algorithm of the transition state.
10) 2001: MOPAC2002 ® Improvement of the package solvate, all atoms of the main group, PM5 method and parameterization for more transition metals.
11) 2004: MOPAC2005 ® Calculation of complex Eu(III) [65] and Th(IV) [66] by Sparkle Model.
12) 2006: MOPAC 7.1 ® A translation of MOPAC 6 for Fortran 90 is available on the Internet, having incorporated the Sparkle/AM1 model for calculating all trivalent lanthanide ions [67] ;
13) 2007: MOPAC2007 ® An application of MOPAC7.1 incorporating new methods of RM1, PM6, Sparkle/ AM1 and Sparkle/PM3. This program is available free of charge to the academy and for applications nonprofit [67] .
Several programs two-dimensional of design of molecules are available and easy to use, as ChemWindow, Isis Draw, ChemDraw [68] and Chem3D [69] . They allow the preparation of figures and diagrams with desired quality and accuracy and facilitate the documentation and scientific communication. The software ChemSketch 12.00 [23] is an advanced design that provides chemical molecular properties, optimization and 3D visualization, ability to name the molecules, as IUPAC, and still has a large database of chemical structures and laboratory materials. The software automatically calculates the valence of each atom and restricts the construction of the molecule based on the octet rule, unless instructed to do this restriction. Then is possible to request the construction of 3D spatial form of the species studied, which triggers another window where the academic can rotate tridimensionally the species studied, in addition to observing these species in different visualizations with possibility to visualize bonds and spatial arrangement of species prominently in each of these representations. The design and visualization of 3D drugs, with steric factors relevant to biological activity, are important for analysis of the size, volume and shape of the molecules [70] . The Molekel is a free software multiplatform molecular visualization. It was originally developed at the University of Geneva by Flükiger in the 1990s for Silicon Graphics computers. In 1998, Stefan Portmann took responsibility and released version 3.0. The version 4.0 was almost one version of the platform independent. Other developments lead version 4.3, before Stefan Portman moved and stopped developing the codes. In 2006, the Swiss National Supercomputing Centre (CSCS) restarted the project and version 5.0 was released on December 21 of the same year [24] .
To obtain the conformational analysis and energy minimization, we can cite: the program Chem3D [69] widely used in studies with this objective [70] . However, other programs like Molecular Modeling Pro [71] , ChemSite (ChemSW) [72] , Alchemy, Sybyl, ChemX, cache and WebLab Viewer are also available.
In the area of molecular modeling, graphics construction and projects of drugs, the program Hyperchem [73] for being a tool specializing in 3D structures of interest to the medical, pharmaceutical and organic chemistry. The program lets you design complicated molecules. This software is also an alternative in the field of spectroscopy, which besides the ability to simulate a priori by the NMR spectra quantum methods, contains a database of approximately 104 molecules applicable to macromolecules as well as small molecules. The software also includes animations, and quantum chemical calculations and molecular mechanics.
The choice of method for energy minimization depends on factors related to the size of the molecule, parameters of availability and stored data and computational resources. Molecular models generated by the computer are the result of mathematical equations that estimate the positions and properties of the electrons and nuclei, the calculations exploit experimentally, the characteristics of a structure, providing a new perspective on the molecule [74] .
In quantum chemistry the softwares more used are Gaussian and GaussView that uses the laws of quantum mechanics to predict the energies, structures and properties and vibrational frequency of molecular systems [75] . The GaussView 5.0 is a program that can work on Windows and responsible for building the structures under study, by viewing these as well as for generating the input of the species under study for the program calculations–Gaussian 03W. This includes an advanced molecular modeler, which can be used for construction and molecular dimensions of the three test [75] .
The Gaussian 03W is a program that can work on Windows and Linux that performs computations used in the study of reaction mechanisms, equilibrium geometries of neutral molecules, radicals and ions, and the determination of physicochemical parameters. Appreciates structure, reactivity, thermodynamic properties, energy barriers (transition states), conformational analysis, employing the optimization of molecules and theoretical calculations of vibrational spectra. From the optimization is obtained the most appropriate structure to the molecule, whereas the lengths and bond angles and power stabilization calculated by 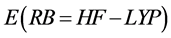 ua [75] .
ua [75] .
6. Application of Hartree-Fock Method Using Computational Tools
Obtaining molecular properties depends of method and basis sets, and represents a means of chemical information contained in the molecular structure of the compound studied. The structure-activity relationships (SAR) represent a core aspect of medicinal chemistry. The fact that a small change in structure leads to a small change in biological activity and allows chemists to rationalize substitutions at specifics positions, giving them the freedom to modify a molecule to improve various properties such as lipophilicity, bioavailability, and so on without sacrificing potency (to a large extent). From the modelers’ perspective, the principle of similar structures having similar activities [76] is a cornerstone of quantitative structure-activity relationship (QSAR) modeling [77] [78] . This information is transformed and encoded for lots of problems chemical, pharmacological and toxicological studies on the relationship between structure-activity, quantitative structure-activity and structure-property (SAR, QSAR and QSPR) [79] -[81] .
Ferreira et al. [82] studied artemisinin and 18 derivatives with antimalarial activity against W-2 strains of Plasmodium falciparum through quantum chemistry and multivariate analysis. The geometry optimization of structures was realized using the Hartree-Fock method and the 3-21G** basis set. Maps of molecular electrostatic potencial and docking molecular were used to investigate the interaction between the ligands and the receptor (Heme).
Santos et al. [83] performed studies using Hartree-Fock method and the 6-31G** basis set were employed to calculate the molecular properties of artemisinin and 20 derivatives with antimalarial activity. Maps of molecular electrostatic potential (MEPs) and molecular docking were used to investigate the interaction between ligands and the receptor (heme). Principal component analysis and hierarchical cluster analysis were employed to select the most important descriptors related to activity. The correlation between biological activity and molecular properties was obtained using the partial least squares and principal component regression methods. The regression PLS and PCR models built in this study were also used to predict the antimalarial activity of 30 new artemisinin compounds with unknown activity. The models obtained showed not only statistical significance but also predictive ability. The significant molecular descriptors related to the compounds with antimalarial activity were the hydration energy (HE), the charge on the O11 oxygen atom (QO11), the torsion angle O1-O2-Fe-N2 (D2) and the maximum rate of R/Sanderson Electronegativity (RTe+). These variables led to a physical and structural explanation of the molecular properties that should be selected for when designing new ligands to be used as antimalarial agents.
Case Study on Aspirin
Aspirin introduced in 1899 was one of the first drugs developed and is still one of the most widely used. Estimated 20 billion aspirin tablets are consumed each year in the United States. Originally planned to ease the pain and relieve sore muscles, proved to be a highly complex drug with the power and unexpected limitations. It turned out that it reduces the incidence of heart attacks and is effective in reducing the incidence of Alzheimer's disease and cancer of the digestive tract. At the same time, however, aspirin attacking the stomach lining, causing bleeding or even ulcers, and usually cause intestinal problems [84] . One of the forms of action of aspirin is blocking an enzyme (a type of protein) called COX-2, which promotes inflammation, pain and fever. Unfortunately, it also interferes with COX-1 a correlate enzyme that produces essential hormones to the health of stomach and kidney. An analgesic and anti-inflammatory agent is efficient in COX-1. Figure 2 is shown the structure of aspirin which acts transferring part of its molecule known as acetyl group, for COX-2, disabling it. This drug-receptor interaction is irreversible nature due to the formation of a covalent bond resulting from the nucleophilic attack of the hydroxyl group of the amino acid serina530 to the electrophilic acetyl grouping present in aspirin [85] .
A substitute for aspirin (new drug) has to keep this aspect of the molecule, and the replacement should the general format and size of the molecule in such a way it clicks into place in molecular target the same manner
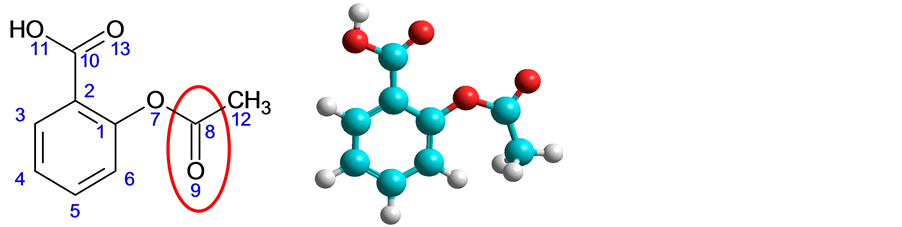
Figure 2. Aspirin (structure) and region essential for the expression of biological (pharmacophore) was visualized using ChemSketch 12.00 program [23] and HyperChem Release 6.02 [73] .
that aspirin.
The use of maps of electrostatic potential (MEP) is a computational tool that aids in the process of recognition of one molecule by another, as interactions of types receptor drugs and enzyme substrates, because being by their potential that chemical species interact with other in biological recognition process. The electronic parameters are one of the main factors governing drug-receptor interaction, in this sense; the MEP can be considered an alternative approach in order to understand the electrostatic contribution of this drug and its new derivatives for biological activity [86] . In the construction of the MEP are necessary three steps: construction of the surface density of the molecule, construction of the electrostatic surface potential and applying colors the surface obtained to designate potential values. One of the frequent topics of theoretical chemistry is research to improve methods to elucidate the behavior of molecules and other reactive chemical species. Among the numerous existing reactivity indices the molecular electrostatic potential 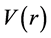 that is generated around a molecule by its nuclei and electrons, is known for being a real physical property can be determined experimentally by diffraction methods, as well as computationally [87] .
that is generated around a molecule by its nuclei and electrons, is known for being a real physical property can be determined experimentally by diffraction methods, as well as computationally [87] .
In Figure 3 are shown the MEPs of aspirin with Hatree-Fock method in different basis sets (HF/3-21G*, HF/ 3-21G**, HF/6-31G, HF/6-31G*, HF/6-31G** and HF/6-311G). In this figure we can observe that in the HF/6-31G** method, showed the lowest positive electrostatic potential (region blue color) of 0.06715 au (atomic unit). However, HF/6-311G method, showed higher positive electrostatic potential 0.07607 au. The variation between them was ±0.00892au (HF/6-311G and HF/6-31G**); Also in this figure we observed that the HF/6-311G method, showed the lowest negative electrostatic potential (region red color) equal to −0.10235 au. However, HF/3-21G** method showed higher negative electrostatic potential of −0.09071 au. The variation between them was ±0.01164 au (HF/6-311G and HF/3-21G**). Thus, the presence of a negative potential surface in carbonyl oxygen atom of the acetyl group is nucleophilic (affinity for positive nuclei), while the carbonyl carbon is electrophilic (electron affinity) in accordance with the literature [85] . Thus, we have shown that the use of different basis sets present values of different electrostatic potentials for the same case study. Therefore, obtaining molecular properties will depend on the method and basis set to reproduce experimental data with greater accuracy. In this case, the MEP of aspirin in different basis set was used to evaluate the key features of aspirin from qualitative comparisons in the region of the acetyl group, which according to Bernardinelli et al. [88] the geometric form of the electrostatic potential is similar for all active compounds. However, new derivatives of aspirin must have some structural similarity in terms of their electrostatic potentials that allow one to be recognized by the other, with similar biological activities [87] [89] [90] .
Structure-activity relationship (SAR) indicates molecular structure modifications that increase the drug effectiveness. In general, reports show that these modifications are made throughout small changes in the leading compound structure, followed by trials in laboratory to quantify the variations in the biological activity due to changes in the molecular structure [91] .
The quantum-chemical descriptors widely used in SAR, QSAR and QSPR studies are related to the energy of the frontier orbitals (HOMO and LUMO). The reason for this is related to the fact that these properties provide information about the character electron donor and/or electron-acceptor and a compound thus forming a charge transfer complex (CTC) [92] . The energy of Highest Occupied Molecular Orbital Energy (HOMO) and Lowest Unoccupied Molecular Orbital Energy (LUMO) are quantum-chemical descriptors, which play an important role in chemical reactions and the formation of many complex charge transfer [93] . In Figure 4 is shown the fron-
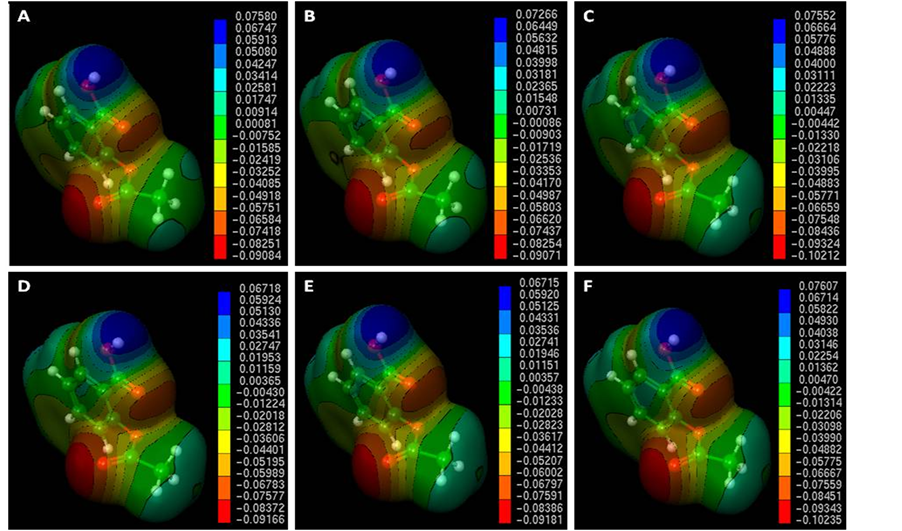
Figure 3. Molecular Electrostatic Potential Map of aspirin in different basis sets (A – HF/3-21 G*, B – HF/3- 21G**, C – HF/6-31G, D – HF 6-31G*, E – HF 6-31G**, F – HF 6-311G). The MEPs were visualized and calculated by the Molekel program [24] .

Figure 4. Orbital’s energy Homo and Lumo of aspirin in different basis sets (A – HF/3-21 G*, B – HF/ 3-21G**, C – HF/6-31G, D – HF 6-31G*, E – HF 6-31G**, F – HF 6-311G). The Homo and Lumo were visualized and calculated by the Molekel program [24] .
tiers orbital (HOMO and LUMO) with the respective values of energy (eV), using Hatree-Fock method at different basis sets (HF/3-21G*, HF/3-21G**, HF/6-31G, HF/6-31G*, HF/6-31G** and HF/6-311G) for aspirin, and this figure we note the delimited region for the HOMO orbital which measures the electron-donor character of aspirin, and the LUMO which measures the electron-acceptor character. From these definitions, two important features can be observed: the higher the energy of the HOMO greater electron-donating ability, which can be observed in HF/6-31G** with a value of HOMO = −0.34408 eV, and the lower the energy of the LUMO will be lowest resistance to accept electrons that can be noticed in HF/6-311G with a value of LUMO = 0.06889 eV. In this figure the HOMO is located in the region around the benzene ring and the acetyl group, when the substituents are made in the aromatic ring or acetyl group, depending on the substituent will have a high electron density, such as the carbonyls, amines or amides, the more pronounced HOMO region is strongly influenced to perform electronic stereo secondary effects, which may compromise the pharmacological activity of the compound. The energy of HOMO is directly related to the ionization potential of the compound and characterizes the ability of the molecule to perform nucleophilic attacks. Also in Figure 4, the LUMO is located in close region to the benzene ring and of the carboxylic group, so the energy of LUMO is directly related to the electron affinity, characterized by the susceptibility of the compound in relation to attacks by nucleophiles [94] .
The energies of HOMO and LUMO have been used for decades as indices of chemical reactivity and are commonly correlated with other indices, such as electron affinity and ionization potential [95] -[99] . The difference between the energies of the HOMO-LUMO orbitals (gap) is an important indicator of molecular stability. Molecules with low gap value are generally reactive, while molecules with higher gap value indicate high stability of the molecule, in the sense of low reactivity in chemical reactions [100] . In Table 1 are shown some molecular properties obtained with Hartree-Fock method in different basis sets (HF/3-21G*, HF/3-21G**, HF/6-31G, HF/6-31G*, HF/6-31G** e HF/6-311G) and the correlation matrix of Pearson [101] -[103] , considering how an independent variant the total energy (Etotal) of aspirin, and other properties as the dependent variable, this treatment was performed using Stastica 6.2 program [104] . In this table it is observed that the correlation between the molecular properties of aspirin is less than or equal to 0.96890 (LUMO), while the correlation between the molecular properties and the total energy is less than or equal to 0.85448 (QC8), which represents the charge on the carbon atom 8, see Figure 2. Among these properties obtained those that had greater relevance to building a model QSPR in function of the total energy were the volume (−0.78677), hydration energy (−0.45775), GAP (−0.43419) and QC8 (0.85448). Therefore, we can represent the QSPR model according to the values of the statistical parameters in Equation (52) below. The statistical quality [105] of the regression equations was gauged by parameters like correlation coefficient (r) or squared correlation coefficient (r2), explained variance ( , i.e., adjusted R2), standard error of estimate (SEE), and variance ratio (F) [106] -[108] . The better regression models were selected on the basis of the higher r, F value (a statistic of assessing the overall significance) and the lower SEE.
, i.e., adjusted R2), standard error of estimate (SEE), and variance ratio (F) [106] -[108] . The better regression models were selected on the basis of the higher r, F value (a statistic of assessing the overall significance) and the lower SEE.
 (52)
(52)
This type of treatment shows that QSPR studies are important to obtain of molecular properties that take into account different aspects of chemical information, this information can be through experiments or theoretical calculations simple counting, consider the entire molecule, fragments or functional groups, knowledge of the 3D structure of the molecule or molecular graphics his or her simply formula, information defined by scalar values, vectors or scalar fields [109] .
In the discovery of a superaspirin Jacob et al. (2012) [110] synthesized by conjugation aspirin-glucose (Figure 5) in order to study the solubility in water and anticancer activity as compared to aspirin and evaluated that aspirin-glucose was seven times more soluble in water than aspirin, and about 8 to 9 times more active in inhibiting cell growth than aspirin in its anticancer activity in cell culture breast, pancreatic, and cell lines prostate, while the activity was similar in a line benign non-cancer cells. According to the computer calculations performed to aspirin and aspirin-glucose in HF/6-31G** verified that the anticancer activity of aspirin-glucose was increased by the fact of presenting high value GAP = −0.43232 eV, having greater molecular stability and low chemical reactivity, being that the value of GAP to aspirin in HF/6-31G** was −0.43332 eV, having a variation of GAP = ±10−3 eV (between aspirin and aspirin-glucose).
In Figure 5 is shown the map of electrostatic potential for aspirin-glucose, and observed the region of negative electrostatic potential, characterized by red color, which is the region essential for the expression of biological activity (pharmacophore). Therefore, these results are directly related with the conclusion that Jacob et al. indicated that the hydrolysis of the aspirin-glucose in human serum is at a relatively slower rate compared to aspirin where there has been significant anticancer activity at the doses studied under the experimental conditions.
Table 1. Molecular properties obtained at different basis sets of aspirin and Pearson correlation matrix.
Figure 5. (a) The glucose-aspirin structure was visualized using ChemSketch 12.00 program [23] . (b) Map of molecular electrostatic potential (MEP). ((c) and (d)) Orbital’s energy Homo and Lumo. The MEP, Homo and Lumo were visualized and calculated using Hartree-Fock (HF) method and HF/6-31G** basis set by the Molekel program [24] .
The anticancer activity in vitro was much stronger for aspirin-glucose compared to aspirin in cancer cell lines. Therefore, further studies are needed among them we can mention the use of maps of electrostatic potential as an indicator of site of chemical reactivity to confirm this finding in a system in vivo. The high solubility of the conjugated glucose aids the development of a form of injection of aspirin.
This new derivative can be considered in the future a “superaspirin” that must pass safety tests for long periods before being placed on pharmacy shelves, but the time to replace aspirin and other non-steroidal anti-inflammatory drugs.
7. Final Considerations
The computational chemistry is considered as one of the greatest intellectual realizations of the twentieth century, and has been the conceptual basis that allows the understanding of chemistry of a way much deeper than that existing before age 20, epoch wherein were launched the bases of quantum theory. The impact of this theory in chemistry can be verified for its practical implications in various fields such as spectroscopy, electron microscopy, molecular modeling, among others.
The molecular modeling provides important information for the process of drug discovery, because it facilitates obtaining of specific molecular properties of a molecule that can influence the interaction with the receptor and biological activity.
The Hartree-Fock method provides a quantitative prediction of high quality for a wide variety of chemical and biological systems, but the calculations are time consuming and high computational cost. A resource commonly employed is optimizing geometry with a basis set simpler, and then perform calculations “Single Point” with a basis set most complete allowing the determination of energy and other molecular properties of a system, using a base of more sophisticated calculation.
The application of the Hartree-Fock method depends on the basis set and of system to be studied to obtain different molecular properties related to the biological activity of bioactive molecules. The computer calculations should describe the necessary characteristics related to the experimental data of the molecule or set of molecules under study, for that molecular modeling can be represented of effective and/or efficient form. However, these descriptors are not completely universal, because they are dependent on the structures and systems studied. Even though it is based on a minimum of energy, the calculated descriptors have values very close to their respective empirical values and indicate trends electronic systems under study. The aspects highlighted in this work are evident, therefore, the quantum-chemical descriptors have a wide range of applications in SAR, QSAR and QSPR studies, as well as in many areas of integration of fundamental knowledge of Organic Chemistry, Biochemistry, Molecular Biology, Pharmacology and Pharmaceutical Chemistry.
Acknowledgements
We gratefully acknowledge the financial support of the Brazilian Agency National Council of Scientific and Technological Development (CNPq Proc. 306676/2010-9). The authors would like to thank the Postgraduate Program in Biotechnology and Biodiversity—Network BIONORTE and to the Laboratory of Modeling and Computational Chemistry, Federal University of Amapá for the computational support.
References
- Luna, J.S., Santos, A.F., Lima, M.R.F., Omena, M.C., Mendonça, F.A.C., Bieber, L.W. and Sant’Ana, A.E.G. (2005) A Study of the Larvicidal and Molluscicidal Activities of Some Medicinal Plants from Northeast Brazil. Journal of Ethnopharmacology, 97, 199-206. http://dx.doi.org/10.1016/j.jep.2004.10.004
- Amarante, C.B., Müller, A.H., Póvoa, M.M. and Dolabela, M.F. (2011) Estudo Fitoquímico Biomonitorado Pelos Ensaios de Toxicidade Frente à Artemia Salina e de Atividade Antiplasmódica do Caule de Aninga (Montrichardia linifera). Acta Amazônica, 41, 431-434. http://dx.doi.org/10.1590/S0044-59672011000300015
- Robards, K., Prenzler, P.D., Tucker, G., Swatsitang, P. and Glover, W. (2003) Phenolic Compounds and Their Role in Oxidative Processes in Fruits. Food Chemistry, 66, 401-436. http://dx.doi.org/10.1016/S0308-8146(99)00093-X
- Moure, A., Cruz, J., Franco, D., Dominguez, J., Sineiro, J., Dominguez, H., Nnunez, M. and Parajó, J. (2001) Natural Antioxidants from Residual Sources. Food Chemistry, 72, 145-171. http://dx.doi.org/10.1016/S0308-8146(00)00223-5
- Huang, D., Ou, B. and Prior, R.L. (2005) The Chemistry behind Antioxidant Capacity Assays. Journal of Agricultural and Food Chemistry, 53, 1841-1856. http://dx.doi.org/10.1021/jf030723c
- Zibadi, S., Farid, R., Moriguchi, S., Lu, Y., Foo, L., Tehrani, P., Lreich, J. and Watson, R. (2007) Oral Administration of Purple Passion Fruit Peel Extract Attenuates Blood Pressure in Female Spontaneously Hypertensive Rats and Humans. Nutrition Research, 27, 408-416. http://dx.doi.org/10.1016/j.nutres.2007.05.004
- Sun, J., Chu, Y.F., Wu, X. and Liu, R.H. (2002) Antioxidant and Antiproliferative Activities of Common Fruits. Journal of Agricultural and Food Chemistry, 50, 7449-7454. http://dx.doi.org/10.1021/jf0207530
- Amarante, C.B., Silva, J.C.F., Solano, F.A.R., Nascimento, L.D., Moraes, L.G., Silva, G.F. and Uno, W.S. (2009) Spectrometric Study of the Leaves of Aninga (Montrichardia linifera) Collected from the Guama River, Campus of UFPA, Belém-PA. A Contribution to the Chemical Study of the Araceae Family. Revista Científica da UFPA, 7, 1-19.
- D’Oliveira, H.V. (1854) System of Brazilian Vegetable Materia Medica. Casa de Eduardo & Henrique Laemmert, Rio de Janeiro.
- Moreira, N.J. (1862) Dictionary of Brazilian Medicinal Plants. Typographia do Correio Mercantil, Rio de Janeiro.
- Catsro, J.M. (1878) Purgatives Brazil’s Indigenous. Faculdade de Medicina do Rio de Janeiro.
- Fenner, R., Betti, A.H., Mentz, L.A. and Rates, S.M.K. (2006) Plantas Utilizadas na Medicina Popular Brasileira com Potencial Atividade Antifúngica. Revista Brasileira de Ciências Farmacêuticas, 42, 369-394. http://dx.doi.org/10.1590/S1516-93322006000300007
- Moo-Puc, R., Robledo, D. and Freile-Pelegrin, Y. (2008) Evaluation of Selected Tropical Seaweeds for in Vitro AntiTrichomonal Activity. Journal of Ethnopharmacology, 120, 92-97. http://dx.doi.org/10.1016/j.jep.2008.07.035
- Osorio, D.E.J., Montoya, P.G.L. and Arango, A.G.J. (2006) Alkaloidal Natural Products with Antiprotozoal Activity. Vitae, 13, 61-84.
- Vikas, D.K., Vishweshwar, R. and Lakshmi, N.M. (2000) Current Status of Artemisinin and Its Derivatives as Antimalarial Drugs. Life Science, 66, 279-300.
- Amarante, C.B., Silva, J.C.F., Müller, R.C.S. and Müller, A.H. (2011) Avaliação da Composição Mineral Do Chá da Folha Senescente de Montrichardia linifera (Arruda) Schott (Araceae) por Espectrometria de Absorção Atômica com Chama (FAAS). Química Nova, 34, 419-423. http://dx.doi.org/10.1590/S0100-40422011000300010
- Meshnick, S.R., Jefford, C.W., Posner, G.H., Avery, M.A. and Peters, W. (1996) Second-Generation Antimalarial Endoperoxides. Parasitology Today, 12, 79-82. http://dx.doi.org/10.1016/0169-4758(96)80660-0
- Klayman, D.L. (1985) Qinghaosu (Artemisinin): An Antima-Larial Drug from China. Science, 228, 1049-1055. http://dx.doi.org/10.1126/science.3887571
- Pinheiro, J.C., Ferreira, M.M.C. and Romero, O.A.S. (2001) Antimalarial Activity of Dihydroartemisinin Derivatives against P. falciparum Resistant to Mefloquine: A Quantum Chemical and Multivariate Study. Journal of Molecular Structure: THEOCHEM, 572, 35-44. http://dx.doi.org/10.1016/S0166-1280(01)00522-X
- Pinheiro, J.C., Kiralj, R., Ferreira, M.M.C. and Romero, O.A.S. (2003) Artemisinin Derivatives with Antimalarial Activity against Plasmodium falciparum Designed with the Aid of Quantum Chemical and Partial Least Squares Methods. QSAR & Combinatorial Science, 22, 830-842. http://dx.doi.org/10.1002/qsar.200330829
- Cardoso, F.J.B., Figueiredo, A.F., Lobato, M.S., Miranda, R.M., Almeida, R.C.O. and Pinheiro, J.C. (2008) A Study on Antimalarial Artemisinin Derivatives Using MEP Maps and Multivariate QSAR. Journal of Molecular Modeling, 14, 39-48. http://dx.doi.org/10.1007/s00894-007-0249-9
- Atkins, P. and Jones, L. (2002) Chemical Principles: The Quest for Insight. Freeman, New York.
- ACD/Chemsketch Freware, version 12.00. (2010) Advanced Chemistry Development, Inc, Toronto.
- Flukiger, P. (2002) Molekel 4.2. Swiss Center for Scientific Computing, Mano.
- Dyer, J.R. (1965) Applications of Absorption Spectroscopy of Organic Compounds. Prentice-Hall, New Jersey.
- Silverstein, R.M., Webster, F.X. and Kiemle, D. (2005) Spectrometric Identification of Organics Compounds. Jhon Wiley & Sons, New Jersey.
- Bunge, A.V. (1979) Introdução a Química Quântica. Edgard Blücher, São Paulo.
- Souza, A.A. and Farias, R.F. (2007) Elementos de Química Quântica. Átomo, Campinas.
- Sant’Anna, C.M.R. (2009) Métodos de Modelagem Molecular Para Estudo e Planejamento de Compostos Bioativos: Uma Introdução. Revista Virtual de Química, 1, 49-57.
- Barreiro, E.J. and. Fraga, C.A.M. (2001) Química Medicinal, as Bases Moleculares da Ação dos Fármacos. Artmed, Porto Alegre.
- Nye, M.J. (2007) Working Tools for Theoretical Chemistry: Polanyi, Eyring, and Debates over the “Semiempirical Method”. Journal of Computational Chemistry, 28, 98-108. http://dx.doi.org/10.1002/jcc.20527
- James, H.M. and Coolidge, A.S. (1933) The Ground State of the Hydrogen Molecule. The Journal of Chemical Physics, 1, 825. http://dx.doi.org/10.1063/1.1749252
- Marcus, R.A. (1964) Generalization of the Activated Complex Theory of Reaction Rates. I. Quantum Mechanical Treatment. The Journal of Chemical Physics, 41, 2614-2623. http://dx.doi.org/10.1063/1.1726329
- Hirschfelder, J.O. (1941) Semi-Empirical Calculations of Activation Energies. The Journal of Chemical Physics, 9, 645. http://dx.doi.org/10.1063/1.1750966
- Mielke, S.L., Peterson, K.A., Schwenke, D.W., Garrett, B.C., Truhlar, D.G., Michael, J.V., Su, M.C. and Sutherland, J.W. (2003) H+H2 Thermal Reaction: A Convergence of Theory and Experiment. Physical Review Letters, 91, 63201- 63204. http://dx.doi.org/10.1103/PhysRevLett.91.063201
- Atkinson, R.C. and Suppes, P. (1968) Program in Computer-Assisted Intruction: Final Report. In: Simonson, M.R. and Thompson, A., Eds., Educational Computing Foundations, Prentice Hall, Upper Saddle River.
- Nye, M.J. (2000) Instruments and Experimentation in the History of Chemistry. MIT Press, Cambridge.
- Morgon, N.H. and Coutinho, K. (2007) Métodos de Química Teórica e Modelagem Molecular. Livraria da Física, São Paulo.
- Hartree, D.R. (1928) The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods. Mathematical Proceedings of the Cambridge Philosophical Society, 24, 89-110. http://dx.doi.org/10.1017/S0305004100011919
- Mulliken, R.S. (1932) Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations. Physical Review, 41, 49-71. http://dx.doi.org/10.1103/PhysRev.41.49
- Blinder, S.M. (1965) Basic Concepts of Self-Consistent-Field Theory. American Journal of Physics, 33, 431-520. http://dx.doi.org/10.1119/1.1971665
- Levine, I.N. (1991) Quantum Chemistry. Prentice-Hall, New York.
- Roothaan, C.C.J. (1951) New Developments in Molecular Orbital Theory. Reviews of Modern Physics, 23, 69-89. http://dx.doi.org/10.1103/RevModPhys.23.69
- Clementi, E. and Raimondi, D.L. (1963) Atomic Screening Constants from SCF Functions. The Journal of Chemical Physics, 38, 2686-2689. http://dx.doi.org/10.1063/1.1733573
- Clementi, E., Raimondi, D.L. and Reinhardt, W.P. (1967) Constantes Triagem Atômicas de SCF Funções. II. Átomos com 37-86 Elétrons. The Journal of Chemical Physics, 47, 1300-1307. http://dx.doi.org/10.1063/1.1712084
- Hoffmann, R., (1963) An Extended Huckel Theory. I. Hydrocarbons. The Journal of Chemical Physics, 39, 1397-1412. http://dx.doi.org/10.1063/1.1734456
- Pople, J.A. and Beveridge, D.L. (1970) Aproximate Molecular Orbital Theory. McGraw-Hill, New York.
- Boys, S.F. (1950) Electronic Wave Functions. I. A General Method of Calculation for the Stationary States of Any Molecular System. Proceedings of the Royal Society A, 200, 542-554. http://dx.doi.org/10.1098/rspa.1950.0036
- Shavitt, I. (1963) The Gaussian Function in Calculations of Statistical Mechanics and Quantum Mechanics. In: Alder, B., Fernbach, S. and Rotenberg, M., Eds., Methods in Computational Physics, Academic Press, New York, 1-45.
- Hehre, W.J., Stewart, R.F. and Pople, J.A. (1969) Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals. The Journal of Chemical Physics, 51, 2657-2664. http://dx.doi.org/10.1063/1.1672392
- Stewart, R.F. (1969) Small Gaussian Expansions of Atomic Orbitals. The Journal of Chemical Physics, 50, 2485-2495. http://dx.doi.org/10.1063/1.1671406
- Mulliken, R.S. and Liu, B. (1971) Self-Consistent-Field Wave Functions of P2 and PO, and the Role of d Functions in Chemical Bonding and of s-p Hybridization in N2 and P2. Journal of the American Chemical Society, 93, 6738-6744. http://dx.doi.org/10.1021/ja00754a004
- Hehre, W. (1986) Ab Initio Molecular Orbital Theory. John Wiley & Sons, New York, 678-682.
- Santos, C.B.R., Lobato, C.C., Vieira, J.B., Brasil, D.S.B., Brito, A.U., Macêdo, W.J.C., Carvalho, J.C.T. and Pinheiro, J.C. (2013) Evaluation of Quantum Chemical Methods and Basis Sets Applied in the Molecular Modeling of Artemisinin. Computational Molecular Bioscience, 3, 66-79. http://dx.doi.org/10.4236/cmb.2013.33009
- Stewart, J.J.P. (1999) MOPAC2002. Fujitsu Limited, Tokyo. http://www.cachesoftware.com/
- Clark, T. (2002) VAMP, Computer Cahemie Centrum. Friedrich-Alexander-Universität Erlangen-Nürnberg, Nägelsbachstra Be 25, D-91052, Erlangen.
- Thiel, W. (1998) MNDO97. Organisch-Chemisches Institut, Universitaet Zuerich, Winterthurerstrasse 190, CH-8057, Zuerich.
- Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Zakrzewski, V.G., Montgomery Jr., J.A., Stratmann, R.E., Burant, J.C., Dapprich, S., Millam, J.M., Daniels, A.D., Kudin, K.N., Strain, M.C., Frakas, O., Tomasi, J., Barone, V., Cossi, M., Cammi, R., Mennucci, B., Pomelli, C., Adamo, C., Clifford, S., Ochterski, J., Pettersson, G.A., Ayala, P.Y., Cui, Q., Morokuma, K., Malick, D.K., Rabuck, A.D., Raghavachari, K., Foresman, J.B., Cioslowski, J., Ortiz, J.V., Baboul, A.G., Stefanov, B.B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I., Gomperts, R., Martin, R.L., Fox, D.J., Keith, T., Al-Laham, M.A., Peng, C.Y., Nanayakkara, A., Gonzalez, C., Challacombe, M., Gill, P.M.W., Johnson, B., Chen, W., Wong, M.W., Andres, J.L., Gonzalez, C., Head-Gordon, M., Replogle, E.S. and Pople, J.A. (1998) Gaussian 98, Revision A. 7, Gaussian, Inc., Pittsburgh.
- SPARTAN, Wavefunction, Inc., 18401, Von Karman Avenue, Suite 370, Irvine CA 92612 USA.
- Gordon, M., GAMESS, Gilman Hall, Iowa State University (Ames).
- CambridgeSoft Corporation (1999) Chem3D. Cambridge.
- Ostlund, N. (1993) HyperChem. Hypercube Inc., Gainesville
- Zerner, M.C. (1998) ZINDO Manual. QTP, University Of Florida, Gainesville, 32611-38435.
- Ranaldi, D., Hoggan, P.E., Cartier, A., Baka, K., Mornard, G., Thery, V., Loos, M., Mokrane, A. and Dillet, V. (2003) GEOMOS Manual. Laboratorie de Chimie Théorique, Université de Nancy I, Nancy.
- Rocha, G.B., Freire, R.O., da Costa Jr., N.B., de Sá, G.F. and Simas, A.M. (2004) Sparkle Model for AM1 Calculation of Lanthanide Complexes: Improved Parameters for Europium. Inorganic Chemistry, 43, 2346-2354. http://dx.doi.org/10.1021/ic034882p
- Young, D.C. (2001) Computational Chemistry—A Practical Guide for Applying Techniques to Real-World Problems. Cytoclonal Pharmaceutics Inc., John Wiley & Sons, Inc., New York.
- Stewart, J.J.P. (2007) MOPAC2007, Stewart Computational Chemistry EUA. http://openmopac.net
- Cambridge Soft Corporation (1998) CS ChemDraw 5.0, Chemical Strutucture Drawing Standard. Cambridge.
- Cambridge Soft Corporation (1998) CS Chem3D 5.0, Molecular Modeling and Analysis. Cambridge.
- Carvalho, I., Pupo, M.T., Borges, A.D.L. and Bernardes, L.S.C. (2003) Introdução A Modelagem Molecular de Fármacos no Curso Experimental de Química Farmacêutica. Quimica Nova, 26, 428-438. http://dx.doi.org/10.1590/S0100-40422003000300023
- ChemSW®, Inc., (2001) Molecular Modeling ProTM4.0, Computational Chemistry Program. ChemSW®, Inc., Fairfield.
- ChemSW® Inc., (2001) ChemSite: Interative 3D Molecular Modeling. ChemSW®, Inc., Fairfield.
- Chemplus, Modular Extensions for HyperChem Release 6.02, Molecular Modeling for Windows. (2000) HyperClub, Inc, Gainesville.
- Patrick, G.L. (2001) An Introduction to Medicinal Chemistry. Oxford University Press, Oxford.
- Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Montgomery Jr., J.A., Vreven, T., Kudin, K.N., Burant, J.C., Millam, J.M., Iyengar, S.S., Tomasi, J., Barone, V., Mennucci, B., Cossi, M., Scalmani, G., Rega, N., Petersson, G.A., Nakatsuji, H., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li, X., Knox, J.E., Hratchian, H.P., Cross, J.B., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R.E., Yazyev, O., Austin, A.J., Cammi, R., Pomelli, C., Ochterski, J.W., Ayala, P.Y., Morokuma, K., Voth, G.A., Salvador, P., Dannenberg, J.J., Zakrzewski, V.G., Dapprich, S., Daniels, A.D., Strain, M.C., Farkas, O., Malick, D.K., Rabuck, A.D., Raghavachari, K., Foresman, J.B., Ortiz, J.V., Cui, Q., Baboul, A.G., Clifford, S., Cioslowski, J., Stefanov, B.B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I., Martin, R.L., Fox, D.J., Keith, T., Al-Laham, M.A., Peng, C.Y., Nanayakkara, A., Challacombe, M., Gill, P.M.W., Johnson, B., Chen, W., Wong, M.W., Gonzalez, C. and Pople, J.A. (2004) Gaussian 03, Revision C.02. Gaussian, Inc., Wallingford.
- Johnson, M. and Maggiora, G. (1990) Concepts and Applications of Molecular Similarity. John Wiley & Sons, New York.
- Leach, A. (2001) Molecular Modelling: Principles and Applications. Prentice Hall, Englewood Cliffs.
- Martin, Y. (2010) Quantitative Drug Design: A Critical Introduction. 2nd Edition, CRC Press, Boca Raton. http://dx.doi.org/10.1201/9781420071009
- Todeschini, R. and Gramatica, P. (1997) WHIM-3D 3.3. Milano.
- Todeschini, R. and Gramatica, P. (1998) New 3D Molecular Descriptors: The WHIM and QSAR Applications. Perspectives in Drug Discovery and Design, 9-11, 355-380. http://dx.doi.org/10.1023/A:1027284627085
- Guha, R. (2012) Exploring Structure-Activity Data Using the Landscape Paradigm. Wiley Interdisciplinary Reviews: Computational Molecular Science, 2, 829-841. http://dx.doi.org/10.1002/wcms.1087
- Ferreira, J.E.V., Figueiredo, A.F., Barbosa, J.P., Cristino, M.G.G., Macêdo, W.J.C., Silva, O.P.P., Malheiros, B.V., Serra, R.T.A. and Pinheiro, J.C. (2010) A Study of New Antimalarial Artemisinins through Molecular Modeling and Multivariate Analysis. Journal of the Serbian Chemical Society, 75, 1533-1548. http://dx.doi.org/10.2298/JSC100126124F
- Santos, C.B.R., Vieira, J.B., Lobato, C.C., Hage-Melim, L.I.S., Souto, R.N.P., Lima, C.S., Costa, E.V.M., Brasil, D.S.B., Macêdo, W.J.C. and Carvalho, J.C.T. (2014) A SAR and QSAR Study of New Artemisinin Compounds with Antimalarial Activity. Molecules, 19, 367-399. http://dx.doi.org/10.3390/molecules19010367
- Flower, R. (2003) What Are All the Things that Aspirin Does? British Medical Journal, 327, 572-573. http://dx.doi.org/10.1136/bmj.327.7415.572
- Fraga, C.A.M. (2001) Razões da Atividade Biológica: Interações Microe Biomacromoléculas. Química Nova na Escola, São Paulo-SP, 33-42.
- Santos, C.B.R., Lobato, C.C., Sousa, M.A.C., Macêdo, W.J.C. and Carvalho, J.C.T. (2014) Molecular Modeling: Origin, Fundamental Concepts and Applications Using Structure-Activity Relationship and Quantitative Structure-Activity Relationship. Reviews in Theoretical Science, 2, 91-115. http://dx.doi.org/10.1166/rits.2014.1016
- Politzer, P. and Murray, J.S. (2002) The Fundamental Nature and Role of the Electrostatic Potential in Atoms and Molecules. Theoretical Chemistry Accounts, 108, 134-142. http://dx.doi.org/10.1007/s00214-002-0363-9
- Bernardinelli, G., Jefford, C.W., Maric, D., Thomson, C. and Weber, J. (1994) Computational Studies of the Structures and Molecules. International Journal Quantum Chemistry, 52, 117-131. http://dx.doi.org/10.1002/qua.560520710
- Murray, J.S. and Politzer, P. (2011) The Electrostatic Potential: An Overview. Wiley Interdisciplinary Reviews: Computional Molecular Science, 1, 153-163. http://dx.doi.org/10.1002/wcms.19
- Galabov, B., Ilieva, S., Koleva, G., Allen, W.D., Schaefer III, H.F. and Schleyer, P.V.R. (2013) Structure-Reactivity Relationships for Aromatic Molecules: Electrostatic Potentials at Nuclei and Electrophile Affinity Indices. Wiley Interdisciplinary Reviews: Computational Molecular Science, 3, 37-55. http://dx.doi.org/10.1002/wcms.1112
- Martins, G.R., Napolitano, H.B., Camargo, L.T.F.M. and Camargo, A.J. (2012) Structure-Activity Relationship Study of Rutaecarpine Analogous Active against Central Nervous System Cancer. Journal of the Brazilian Chemical Society, 23, 2183-2190. http://dx.doi.org/10.1590/S0103-50532013005000004
- Honório, K.M. and Silva, A.B.F. (2003) An AM1 Study on the Electron-Donating and Electron-Accepting Character of Biomolecules. International Journal of Quantum Chemistry, 95, 126-132. http://dx.doi.org/10.1002/qua.10661
- Hirao, H. (2011) Correlation Diagram Approach as a Tool for Interpreting Chemistry: An Introductory Overview. Wiley Interdisciplinary Reviews: Computational Molecular Science, 1, 337-349. http://dx.doi.org/10.1002/wcms.20
- Grant, G.H. and Richards, W.G. (1996) Computational Chemistry. Oxford Science Publications, Oxford.
- Contreras, R., Domingo, L.R., Andrés, J., Pérez, P. and Tapia, O. (1999) Nonlocal (Pair Site) Reactivity from SecondOrder Static Density Response Function: Gasand Solution-Phase Reactivity of the Acetaldehyde Enolate as a Test Case. The Journal of Physical Chemistry A, 103, 1291-1436. http://dx.doi.org/10.1021/jp982801i
- Clare, B.W. (1995) The Relationship of Charge Transfer Complexes to Frontier Orbital Energies in QSAR. Journal of Molecular Structure: Theochem, 331, 63-78. http://dx.doi.org/10.1016/0166-1280(94)03783-H
- Clare, B.W. (1995) Charge Transfer Complexes and Frontier Orbital Energies in QSAR: A Congeneric Series of Electron Acceptors. Journal of Molecular Structure: Theochem, 337, 139-150. http://dx.doi.org/10.1016/0166-1280(95)04135-S
- Clare, B.W. (1994) Frontier Orbital Energies in Quantitative Structure-Activity Relationships: A Comparison of Quantum Chemical Methods. Theoretical Chemistry Accounts, 87, 415-430. http://dx.doi.org/10.1007/BF01127805
- Heaton, C.A., Miller, A.K. and Powell, R.L. (2001) Predicting the Reactivity of Fluorinated Compounds with Copper Using Semi-Empirical Calculations. Journal of Fluorine Chemistry, 107, 1-3. http://dx.doi.org/10.1016/S0022-1139(00)00324-9
- Zhang, G. and Musgrave, C.B. (2007) Comparison of DFT Methods for Molecular Orbital Eigenvalue Calculations. The Journal of Physical Chemistry, 111, 1554-1561. http://dx.doi.org/10.1021/jp061633o
- Comelli, N.C., Duchowicz, P.R., Lobayan, R.M., Jubert, A.H. and Castro, E.A. (2012) QSPR Study of Valproic Acid and Its Functionalized Derivates. Molecular Informatics, 31, 181-188. http://dx.doi.org/10.1002/minf.201100119
- Tropsha, A. (2010) Best Practices for Qsar Model Development, Validation and Exploitation. Molecular Informatics, 29, 476-488. http://dx.doi.org/10.1002/minf.201000061
- Barbosa, J.P., Ferreira, J.E.V., Figueiredo, A.F., Almeida, R.C.O., Silva, O.P.P., Carvalho, J.R.C., Cristino, M.G.G., Pinheiro, J.C., Vieira, J.L.F. and Serra, R.T.A. (2011) Molecular Modeling and Chemometric Study of Anticancer Derivatives of Artemisinin. Journal of the Serbian Chemical Society, 76, 1263-1282. http://dx.doi.org/10.2298/JSC111227111B
- STATISTICA (Data Analysis Software System). (2004) Version 6.1. StatSoft, Inc., Tulsa. http://www.statsoft.com
- Snedecor, G.W. and Cochran, W.G. (1967) Statistical Methods. Oxford and IBH, New Delhi, 381-418.
- Chatterjee, S., Hadi, A.S. and Price, B. (2000) Regression Analysis by Examples. 3rd Edition, Wiley VCH, New York.
- Diudea, M.V. (2000) QSPR/QSAR Studies for Molecular Descriptors. Nova Science, Huntingdon, New York.
- Debnath, B., Gayen, S., Bhattacharya, S., Samanta, S. and Jha, T. (2003) QSAR Study on Some Pyrodoacridine Ascididemin Analogues as Anti-Tumor Agents. Bioorganic & Medicinal Chemistry, 11, 5493-5499. http://dx.doi.org/10.1016/j.bmc.2003.09.022
- Santos, C.B.R., Vieira, J.B., Formigosa, A.S., Costa, E.V.M., Pinheiro, M.T., Silva, J.O., Macêdo, W.J.C. and Carvalho, J.C.T. (2014) Validation of Computational Methods Applied in Molecular Modeling of Artemisinin with Antimalarial Activity. Journal of Computational and Theoretical Nanoscience, 11, 1-9.
NOTES

*Corresponding author.


