Computational Molecular Bioscience
Vol.2 No.1(2012), Article ID:18268,6 pages DOI:10.4236/cmb.2012.21001
Population Dynamics Approach for the Study of Synergetic Coupling between Antibiotic and Helper Compounds
1Mads Clausen Institute, University of Southern Denmark, Sønderborg, Denmark
2Department of Research, King Christian X’s Rheumatism Hospital, University of Southern Denmark, Odense, Denmark
3Aix-Marseille University, UMR-MD-1, IRBA, Marseille, France
4Institute of Physics and Chemistry, University of Southern Denmark, Denmark
Email: veje@mci.sdu.dk
Received January 2, 2012; revised January 20, 2012; accepted February 10, 2012
Keywords: Reversal of Resistance; Non-Antibiotic; Mathematical Model
ABSTRACT
Non-antibiotics affect bacterial susceptibility towards antibiotics in a multifactorial manner, including perturbation of membrane energetic and a possibly direct interaction with drug efflux transporters themselves. Thus, efflux inhibiting compounds affect susceptibilities to antibiotics that act either intracellular or at the bacterial wall. Therefore they may be applied as helper compounds to conventional antibiotic treatments. A valid definition of the effect of these compounds is crucial. Conventional microbiological quotations such as checkerboard or MIC definition do not discriminate the complexity of a system where several compounds interact with several targets both on the bacterial membrane and soma. We presume the fact, that certain resistance mechanisms, such as efflux, are neither adequately nor precisely monitored, utilizing the established microbiologic screening tools, such as agaror microdilution techniques. In this context this paper may contribute as an innovative step, utilizing mathematic modeling in order to describe interactions on the surface of microorganisms. Thus, mathematical modeling might be a tool which can be adopted to optimize the description of certain forms of bacterial resistance, as well as the influence of antibacterial drugs on such targets which interact with bacterial outer-membrane transport mechanisms. This paper presents modeling of bacterial population dynamics as an attempt to precise complex compound target interaction. Furthermore, the importance of a synergetic coupling term in the model is exemplified by comparison with experimental data of Kumar et al. [1]. A specific procedure for extraction of model coefficients is devised for further experimental studies of the coupling between an antibiotics and a helper compound. In particular, it is found that the scarce experimental data of Kumar et al. [1] can be fitted to the mathematical model demonstrating synergetic effects of non-antibiotics.
1. Introduction
The development of resistance in microorganisms against usual clinical antimicrobial agents is increasing all over the world. New antibacterial molecules and new therapeutic approaches are needed to overcome the multi drug resistance (MDR) and the (XMDR) in severe infectious diseases [1-6].
In the laboratories new methods are needed to predict the different resistance mechanisms [7] active in the microorganisms and to overcome these [8-10]. The classical calculations to be used to estimate synergy/antagonism and indifference in combination treatment with classical antimicrobial agents are insufficient. The (experimentally) pronounced synergy called: REVERSAL OF RESISTANCE between antibiotics and non antibiotics is not always to be found with the classical mathematical estimation models in the clinical microbiology laboratory [11-13].
Reversal of resistance in different biological systems and in microorganisms by help of non antibiotics as “helper compounds”, has been pointed out over the last decade [10,14-16] as one clinical possibility to be utilized in order to reverse bacterial resistance in vivo [10].
Interestingly, one group of compounds which is not described as anti-infective agents is found to be strong candidates for development as “helper compounds”. These are the drugs used for non infectious diseases which can exhibit some antimicrobial activities. Especially the compounds having activity on the peripheral and central nerve system, in humans, seem to be promising. These naturally and synthetic compounds are used in the clinical pharmacology as universal and local anesthetics and as psychopharmacological agents including their stereoisomeric analogues [17]. The common actions of these drugs are their blocking effects on the transporters activity located in different eukaryotic and prokaryotic cell membranes in vitro and in vivo. Furthermore, molecular/genetic principles have significantly contributed to our understanding of the regulation and function of resistance mechanisms [7,18-25].
Anti-microbial agents are inactivated by the following resistance mechanisms [7].
• Inactivation or modification of the antibiotic.
• Target modification or protection.
• Reduced intracellular accumulation caused by reduced permeability and/or increased efflux.
MDR efflux pumps and modification of membrane proteins involved in the antibiotic penetration are based on the regulation of transporters genes. Ongoing studies which focus on the activity of bacterial efflux influenced by phenothiazine’s, confirm the hypothesis, that modification of resistance is related to the inhibition of effluxpumps [14,18,26].
Utilizing these known old drugs as “helper compounds” together with usual clinical antibiotics on MDR and XMDR pathogens in the combination antimicrobial therapy in patients with severe infectious diseases is a challenge. Extended mathematical modeling might be a possibility to predict the best combination of molecules to reach the desired reversal of resistance on the background of clinical microbiological investigations. Also many of the pharmacological kinetic questions to be answered might be calculated in these mathematical models, especially when mathematic modeling is focusing on the above mentioned membrane target sites. The purpose of the present study is to answer a few of the above questions by developing a mathematical model on the background of different in vitro and in vivo microbiological investigations [1,27,28].
2. Modeling of Bacterial Population Dynamics
A set of ordinary differential equations is formulated assuming three dynamic variables: Bacteria concentration N, helper compound concentration P1, and antibiotic concentration P2. Here we emphasize that the bacteria concentration N initially is assumed to be “naïve”, i.e., not previously exposed to antimicrobial agents. The set of equations is as follows:
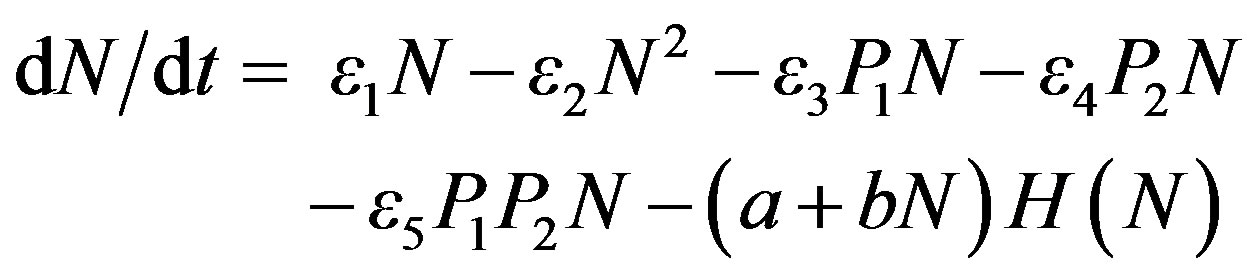 (1)
(1)
where N is the bacteria concentration with N(0) = 1 × 104 CFU/ml, and
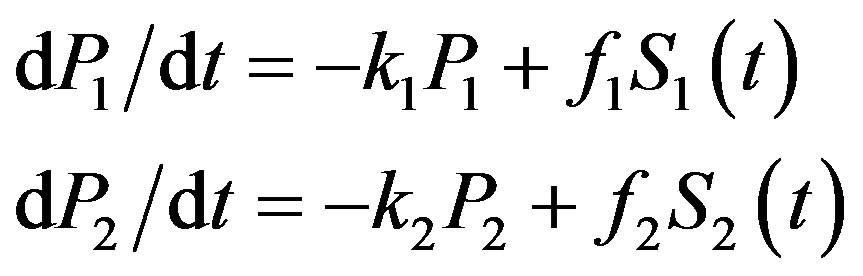 (2)
(2)
are the drug concentrations with Pi(0) = 0 μg/mL. The parameters εi; a; b; ki; fi are constants in the absence of dynamic immunization and H(N) is the Heaviside function. Si(t) is a source function for the injection of drug Pi.
The model takes into account growth of bacteria in the absence of drugs (ε1—term), bacteria interaction phenomena (bacteria food, respiration, and waste restrictions) that limit the upper concentration level of bacteria (ε2), coupling mechanisms between bacteria and helper compound (ε3) as well as bacteria and antibiotics (ε4). For example the ε3 term in the first equation is proportional to the simultaneous concentration of the helper compound P1 and the bacteria concentration N. If ε3 is positive (negative) the coupling term leads to a decrease (increase) in bacteria concentration. An additional multicoupling effect is introduced involving all three dynamic variables (ε5). This coupling reflects the synergy term between the helper compound (P1) and the antibiotics (P2) in decreasing the bacteria concentration. We also include the effect of the host immune defense system by adding a term—(a+bN)H(N) that keeps the bacteria concentration down for controlled infections. A more detailed formulation of the immune defense action similar to that described in [9] could easily be incorporated. The dynamics of the helper compound and antibiotics involve exponential concentration decay over time upon injection in the host (coefficients k1 and k2 corresponding to different decay rates). Drug injections are controlled externally by source terms fiSi(i = 1;2).
A case study involving varying number of active coefficients are carried out and discussed in the following. The general parameter values are listed in Table 1 and used in the case studies unless otherwise stated.
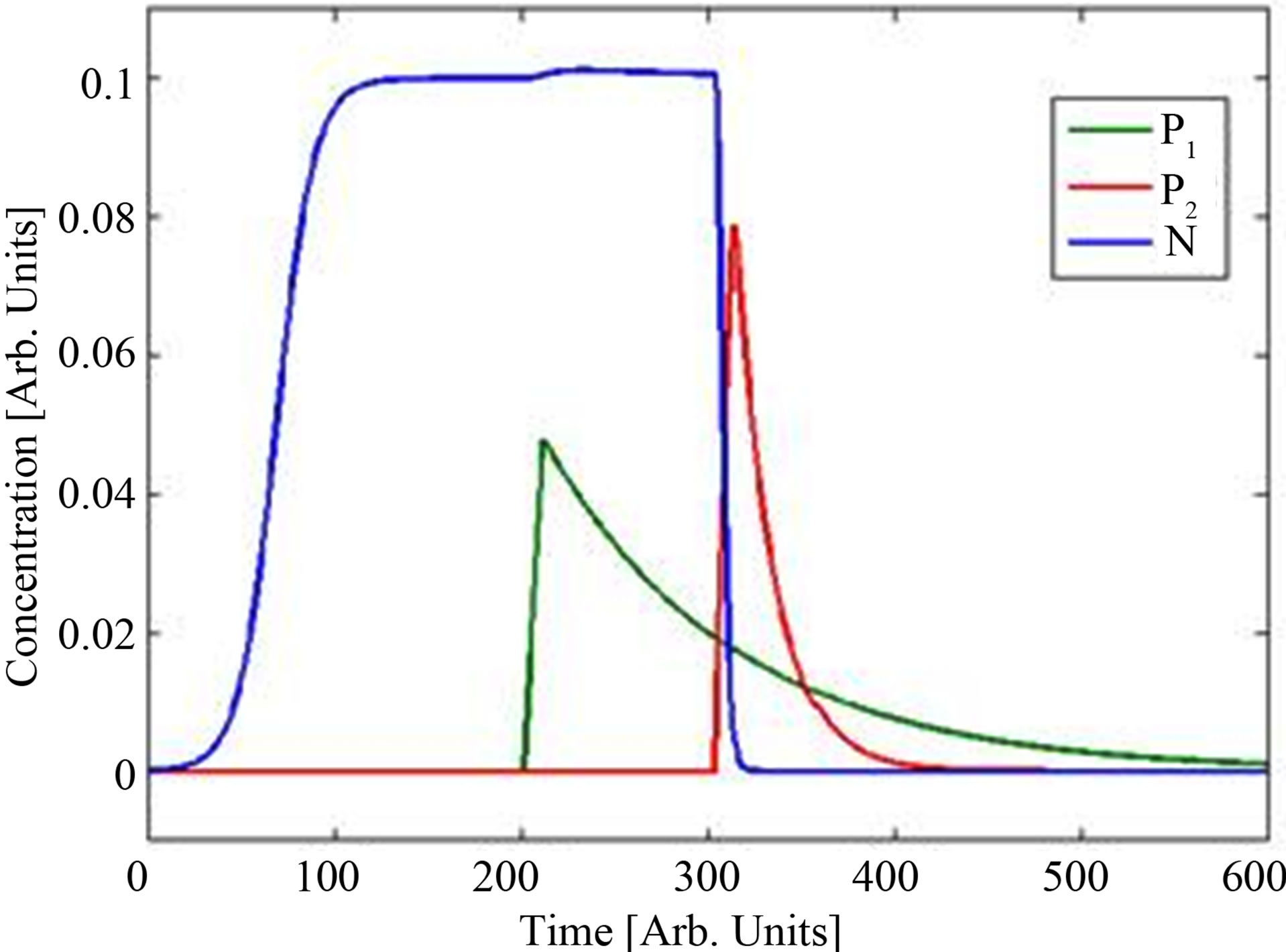
Figure 1 shows the drug injection profiles as function of time Si(t) for the helper compound (blue curve) and the antibiotics (red curve). The terms are normalized so that the integral of Si(t) is unity.
In Figure 2(a), we plot the resulting bacteria concentration dynamics. The injection forcing amplitudes of helper compound and antibiotic is f1 = 0.5 and f2 = 1. Note the exponential increase and subsequent saturation of the bacteria concentration as expected. At the time for the helper compound injection we see the gain effect of
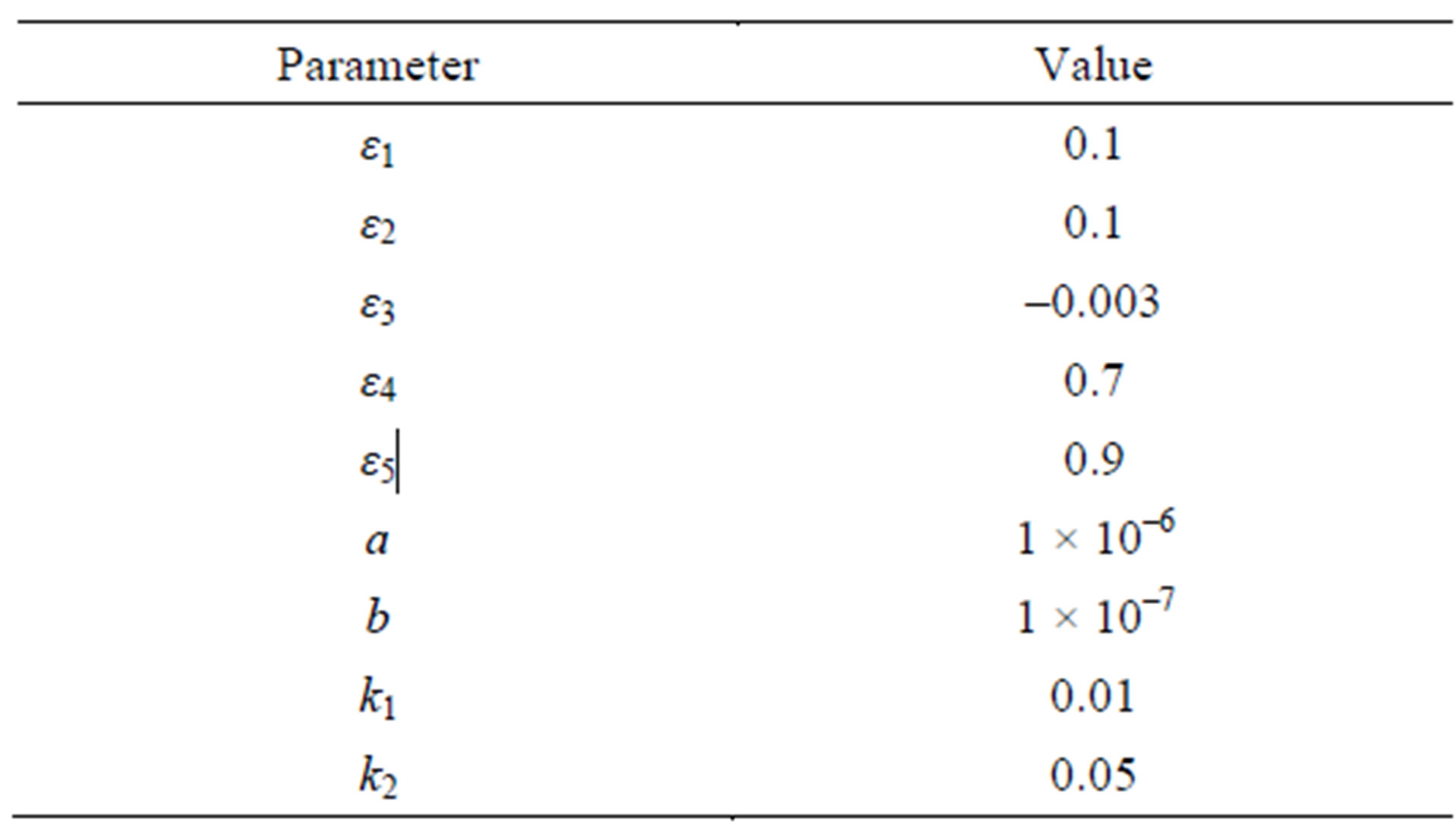
Table 1. Basic parameters for the case studies.
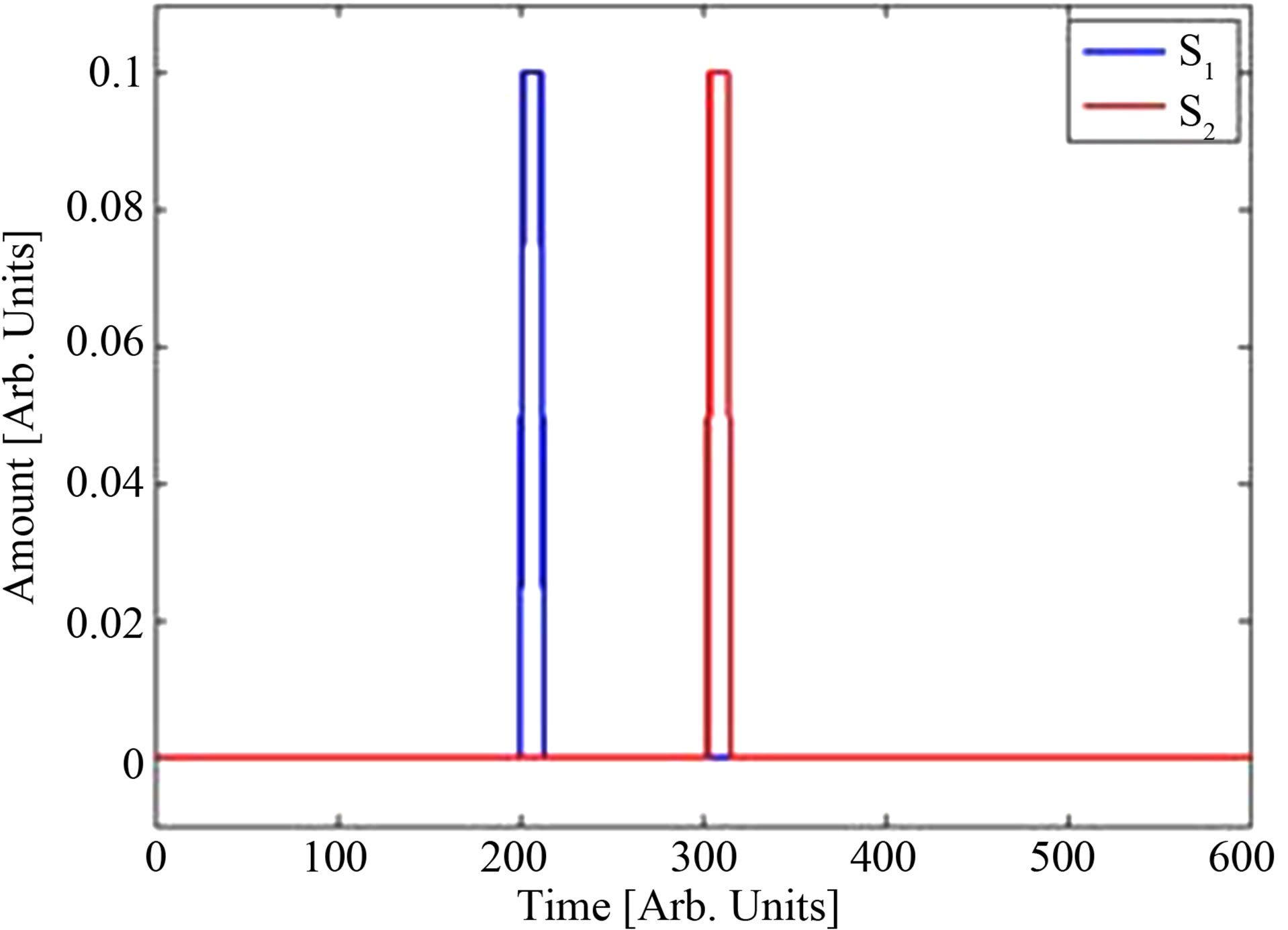
Figure 1. Source functions for P1(t) (blue) and P2(t) (red), f1 = f2 = 1.
 (a)
(a)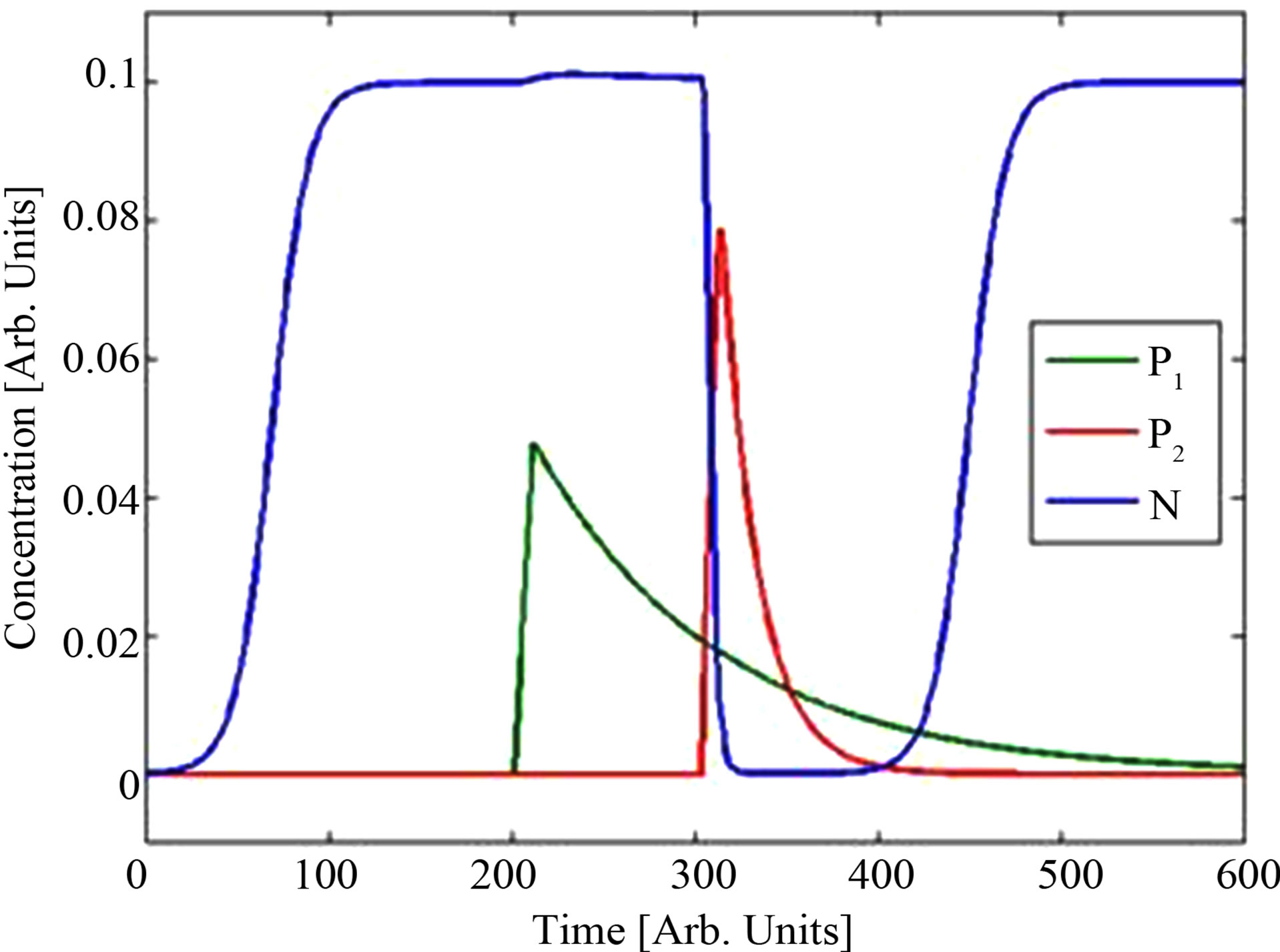 (b)
(b)
Figure 2. (a) Dynamics including coupling term resulting in complete kill. (b) with no coupling term (ε5 = 0) the model results in reactivation of the bacterial level.
the helper compound on the bacteria population (since ε3 is negative).
In Figure 2(a) it is seen that the immune system is strong enough to maintain the bacteria concentration at a low insignificant level in the case where the coupling term is activated. Basically, this case demonstrates a “successful” situation where the addition of antibiotics cures the patient. In the absence of a helper compound the bacterial level will increase again, hence the antibiotic itself is not sufficient. It is only due to the action of the coupling term (represented by ε5) that a successful kill is attained. The term involving ε5 is effective only if both the antibiotic and the helper compound concentrations are nonzero simultaneously! This is demonstrated in Figure 2(b) where we simulate the system with the coupling term (ε5 = 0). In this case, a pure additive model is effected and model results confirm that in the absence of the drug coupling the bacteria population eventually recovers. This demonstrates the gain in coupling drugs so as to obtain a stronger killing of bacteria—even though the effect of the helper compound may be non-antibiotic. Administration times are chosen arbitrarily for the case study considered in Figure 2—it is just an example. In actual fact, our model can easily handle any other administration choice. For the estimation of the mathematical model parameters it is important to be able to administer the addition of helper compound and antibiotics differently as explained below. The set of experimental studies suggested there is a minimum for the determination of all parameters in an unambiguous way and therefore a complete mathematical study.
3. Experimental Characterization of Model Parameters
The above model requires verification using experimental data. In particular, a set of experimental studies is suggested to provide information about model parameters. This protocol of experiments may serve as inspiration to future works aiming to provide experimental basis for development and validation of mathematical models.
Inject helper compound in the absence of bacteria and antibiotics. The dynamic behavior of P1 allows k1 to be determined.
Inject antibiotics compound in the absence of bacteria and helper compound. The dynamic behavior of P2 allows k2 to be determined.
Study the evolution of bacteria population in the absence of helper compound and antibiotics. At least four data points at distinct times allow ε1, ε2, a, and b to be specified.
Now adding a certain amount of helper compound f1S1 (but not antibiotics!) to the bacteria population at a certain time and studying the evolution of the bacteria population allows ε3 to be determined.
Now adding a certain amount of antibiotics f2S2 (but not helper compound!) to the bacteria population at a certain time and studying the evolution of the bacteria population allows ε4 to be determined.
A simple way to obtain the coupling parameter ε5 is to finally add both f1S1 and f2S2 with temporal overlap. Studying the influence of bacteria population allows the last parameter ε5 to be found.
Given the above scenario of experiments, the mathematical model must be verified against independent experimental data involving the same bacteria type, antibiotics, and helper compound.
The present model does not take into account changes in the decay rate of the helper compound due to biological trapping or degradation by bacteria. In principle such effects can be built into the model but to simplify the analysis this is not done here. Our comparison with the experimental data of Kumar et al. [1] in the following section shows that the present model is able to capture the essential dynamics. However, due to the scarce data of Kumar et al. it is not possible to conclude further on these effects.
4. Estimation of Model Coefficients—Case Study on Mice with Amlodipine as Helper Compound and Streptomycin as Antibiotics
In the paper by Kumar et al. [1], a series of measurements were carried out for the sensitivity of bacteria in mice vs. addition of the helper compound Amlopidine (Am) and/ or the antibiotics Streptomycin (Sm). At t = 0 hours, four groups of five mice (20 mice in total) were subject to 1) a passive saline injection, 2) injection of 30 μg Am only, 3) injection of 60 μg Sm only, and 4) injection of both 30 μg Am and 60 μg, respectively. Three hours later (at t = 3 hours), a certain amount of bacteria N (t = 3 hours) was next injected into each of the 20 mice.
Bacteria data were provided for three organs: Heart blood, liver, and spleen. Here we will restrict ourselves to heart blood data for mouse number 1 but other cases can be treated similarly.
For such in-vivo experiments the saturation term is not expected to come into play as the mice are not inoculated with lethal doses of bacteria. We formulate the model as in the following equation:
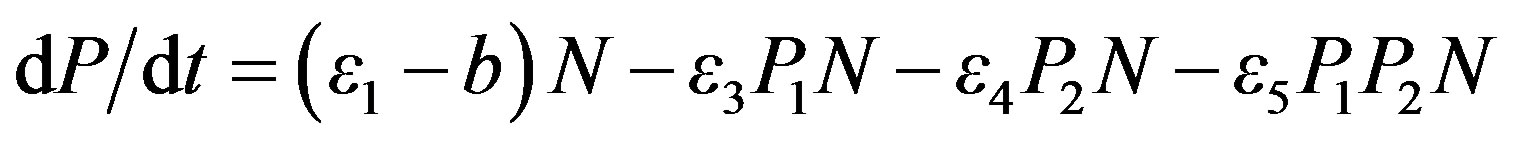 (3)
(3)
where N is the bacteria population with N (t = 3 hours) = 0.9 × 109 CFU/ml, and P1 and P2 are defined as before. The parameter b is the bacteria killing rate due to the mouse immune defense system and other effects not attributed to antibiotic or helper compound killing. This is a slight simplification of 1) and we use 2) as the injection terms similar to the case study.
We make the following assumptions so as to extract the model parameters:
Bacteria are injected at t = 3 hours corresponding to a bacteria concentration equal to N (t = 3 hours) for all mice in all organs.
A mouse is assumed to weigh 20 g and the mouse mass density is 1 g/mL. Adding 30 μg Am then corresponds to 1.5 μg/mL Am. Similarly adding 60 μg Sm corresponds to 3.0 μg/mL Sm.
At t = 18 hours (i.e., 15 hours after the injection of helper compound and/or antibiotics) they register the bacteria population. For 1): 6.5 × 107 CFU/mL, for 2): 2.0 × 106 CFU/mL, for 3): 8.0 × 105 CFU/mL, and for (d): 8.8 × 103 CFU/mL.
The half life t1/2 of Am is 10 hours [2] while for Sm it is 17 minutes [3]. This means that k1 = log 2/t1/2 = 0.069 hours–1 and k2 = log 2/t1/2 = 2.4 hours–1.
We have four data points that allow us to extract information about four of the five quantities: ε1;b; ε3;ε4;ε5. Using a guessed value for ε1 the remaining parameters can be fitted using the data points. If more independent data points were known model parameter verification would be possible.
A calculation procedure is suggested as follows and the accompanying simulation results for the solution of the above set of equations are shown in Figure 3:
Assuming that the in vivo generation time in mice for Salmonella is 20 minutes we get ε1 = 5.776 × 10–4 s–1.
Using the saline injection data, we can calculate b from the ε1 value by increasing b from 0 until the N value at t = 18 hours agrees with the measured value Nsat = 6.5 × 107 CFU/ml. We get b = 6.26 × 10–4s–1. Figure 3 (blue line).
Knowing ε1 and b, we can use the Am injection data to compute ε3 in a similar way until the N value at t = 18 hours agrees with the measured value NAm = 8.8 × 103 CFU/ml. We get ε3 = 8.5 × 10–5 μg–1·mL·s–1. Figure 3 (green line).
Next, knowing ε1 and b, we can use the Sm injection data to compute ε4 until the N value at t = 18 hours agrees with the measured value NSm = 8 × 105 CFU/ml (same procedure as before).
We get ε4 = 1.5 μg–1·mL·s–1. Figure 3 (red line).
Knowing ε1, b, ε3 and ε4, we are now able to use the Am + Sm injection data to compute ε5 in the same manner: We get ε5 = 0.29 μg–1·mL·s–1. Figure 3 (cyan line).
The results for the coefficients are summarized in Table 2.
First we note that ε3 is orders of magnitude smaller than ε4. This shows that the helper compound itself is not effective in killing the bacteria in contrast to the antibiotics. However, the helper compound and the antibiotics together show a synergetic effect which is reflected in the significant value of ε5.
The effect of ε5 can be demonstrated by using the parameters obtained above for the solution of the system but forcing ε5 = 0. This result in a model for the additive
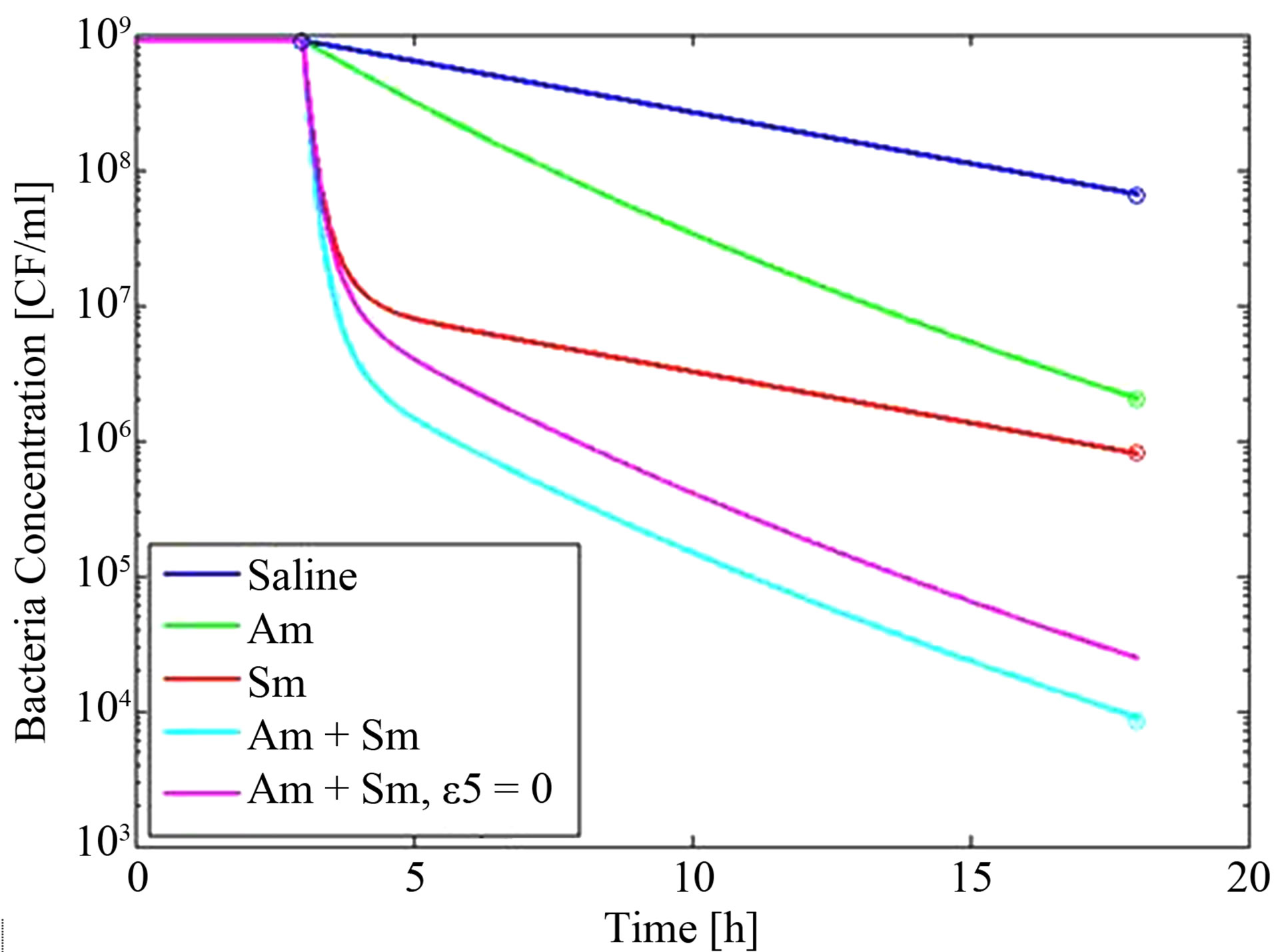
Figure 3. Results for dynamics using the loop procedure described in the text. Lines are for the model and circles are experimental data from Kumar et al. [1].

Table 2. Results for the parameters from the analysis of data from [1].
effect of both Am and Sm without the coupling term—or in other words without the synergetic effect. The result is shown in Figure 3 (purple line) which demonstrates that additive effects alone cannot explain the results obtained by Kumar et al. [1].
5. Summary and Conclusions
We have described a simple population dynamics approach to account for the dynamics of bacteria concentrations during administering of both helper compounds (non-antibiotics) and antibiotics. Using this model we have demonstrated the possibility of the synergetic effect to be the decisive parameter in determining the positive (live) or negative (die) outcome of a given treatment. In addition, this study opens a new field regarding the relationships between the activity of an adjuvant (helper compound) and the structure of used antibiotic molecule: the adjuvant may help the penetration of a selected antibiotic or preserve the efficient intracellular concentration by blocking the efflux pump activity [29]. These two future ways require intensive studies including medicinal chemistry, SAR analyses, molecular modelling and molecular dynamics associated with a rational drug design in order to discriminate and improve the pharmacophoric groups involved in the adjuvant properties.
As a further test we have used a similar model and applied it to the data of Kumar et al. [1]. The analysis presented demonstrates a synergetic antibacterial effect when combining antibiotics (Streptomycin) with helper compound (Amlopidine) and shows that the model can capture the behavior of the few experimental data points available. While the obtained results are encouraging and demonstrate the significance of antibiotics, it is important to emphasize that the experimental data are too scarce to state that the model is completely verified. However, a recipe for further experiments to verify such models has been devised.
5. Acknowledgements
The authors would like to thank the COST Action BM0701 (ATENS) network for stimulating discussions.
REFERENCES
- A. K. Kumar, K. Mazumdar, N. K. Dutta, P. Karak, S. G. Dastidar and R. Ray, “Evaluation of Synergism between the Aminoglycoside Antibiotic Streptomycin and the Cardiovascular Agent Amlodipine,” Biological and Pharmaceutical Bulletin, Vol. 27, No. 7, 2004, pp. 1116-1120. doi:10.1248/bpb.27.1116
- D. A. Stopher, A. P. Beresford, P. V. Macrae and M. J. Humphrey, “The Metabolism and Pharmacokinetics of Amlopidine in Humans and Animals,” Journal of Cardiovascular Pharmacology, Vol. 12, Suppl. 7, 1988, pp. 55-59. doi:10.1097/00005344-198812007-00012
- W. R. Byrne, S. L. Welkos, M. L. Pitt, K. J. Davis, R. P. Brueckner, J. W. Ezzell, G. O. Nelson, J. R. Vaccaro, L. C. Battersby and A. M. Friedlander, “Antibiotic Treatment of Experimental Pneumonic Plague in Mice,” Antimicrobial Agents and Chemotherapy, Vol. 42, No. 3, 1998, pp. 675-681.
- S. Blot, P. Depuydt, K. Vandewoude and D. De Bacquer, “Measuring the Impact of Multidrug Resistance in Nosocomial Infection,” Current Opinion in Infectious Diseases, Vol. 20, No. 4, 2007, pp. 391-396. doi:10.1097/QCO.0b013e32818be6f7
- I. Chopra, C. Schofield, M. Everett, A. O’Neill, K. Miller, M. Wilcox, J. M. Frère, M. Dawson, L. Czaplewski, U. Urleb and P. Courvalin, “Treatment of Health-Care-Associated Infections Caused by Gram-Negative Bacteria: A Consensus Statement,” The Lancet Infectious Diseases, Vol. 8, No. 2, 2008, pp. 133-139. doi:10.1016/S1473-3099(08)70018-5
- M. E. Falagas and I. A. Bliziotis, “Pandrug-Resistant Pandrug-Resistant Gram-Negative Bacteria: The Dawn of the Post-Antibiotic Era?” International Journal of Antimicrobial Agents, Vol. 29, No. 6, 2007, pp. 630-636. doi:10.1016/j.ijantimicag.2006.12.012
- A. Davin-Regli, J. M. Bolla, C. E. James, J. P. Lavigne, J. Chevalier, E. Garnotel, A. Molitor and J.-M. Pagès, “Membrane Permeability and Regulation of Drug ‘Influx and Efflux’ in Enterobacterial Pathogens,” Current Drug Targets, Vol. 9, No. 9, 2008, pp. 750-759. doi:10.2174/138945008785747824
- M. Lipsitch and B. R. Levin, “The Population Dynamics of Antimicrobial Chemotherapy,” Antimicrobial Agents and Chemotherapy, Vol. 41, No. 2, 1997, pp. 363-373.
- A. Handel, E. Margolis and B. R. Levin, “Exploring the Role of the Immune Response in Preventing Antibiotic Resistance,” Journal of Theoretical Biology, Vol. 256, No. 4, 2009, pp. 655-662. doi:10.1016/j.jtbi.2008.10.025
- J. M. Pagès and L. Amaral, “Mechanisms of Drug Efflux and Strategies to Combat Them: Challenging the Efflux Pump of Gram-Negative Bacteria,” Biochimica et Biophysica Acta, Vol. 1794, No. 5, 2009, pp. 826-833.
- K. I. Udekwu, N. Parrish, P. Ankomah, F. Baquero and B. R. Levin, “Functional Relationship between Bacterial Cell Density and the Efficacy of Antibiotics,” Journal of Antimicrobial Chemotherapy, Vol. 63, No. 4, 2009, pp. 745-757. doi:10.1093/jac/dkn554
- J. J. Campion, P. J. McNamara and M. E. Evans, “Pharmacodynamic Modeling of Ciprofloxacin Resistance in Staphylococcus Aureus,” Antimicrobial Agents and Chemotherapy, Vol. 49, No. 1, 2005, pp. 209-219. doi:10.1128/AAC.49.1.209-219.2005
- P. Chung, P. J. McNamara, J. J. Campion and M. E. Evans, “Mechanism-Based Pharmacodynamic Models of Fluoroquinolone Resistance in Staphylococcus aureus,” Antimicrobial Agents and Chemotherapy, Vol. 50, No. 9, 2006, pp. 2957-2965. doi:10.1128/AAC.00736-05
- J. E. Kristiansen, “Antimicrobial Activity of Non-Antibiotics,” ASM News, Vol. 57, 1991, p. 135.
- J. E. Kristiansen, “Chlorpromazine Non-Antibiotics with Antimicrobial Activity-New Insight in Managing Resistance?” Current Opinion in Investigational Drugs, Vol. 2, 1993, pp. 587-591.
- J. E. Kristiansen and L. Amaral, “The Potential Management of Resistant Infections with Non-Antibiotics,” Journal of Antimicrobial Chemotherapy, Vol. 40, No. 3, 1997, pp. 319-327. doi:10.1093/jac/40.3.319
- J. E. Kristiansen, O. Hendricks, T. Delvin, T. S. Butterworth, L. Aagaard, J. B. Christensen, V. C. Flores and H. Keyzer, “Reversal of Resistance in Microorganisms by Help of Non-Antibiotic,” Journal of Antimicrobial Chemotherapy; Vol. 59, No. 6, 2007, pp. 1271-1279. doi:10.1093/jac/dkm071
- G. W. Kaatz, V. V. Moudgal, S. M. Seo and J. E. Kristiansen, “Phenothiazines and Thioxanthenes Inhibit Multidrug Efflux Pump Activity in Staphylococcus aureus,” Antimicrobial Agents and Chemotherapy, Vol. 47, No. 2, 2003, pp. 719-726. doi:10.1128/AAC.47.2.719-726.2003
- O. Lomovskaya, M. S. Warren, A. Lee, J. Galazzo, R. Fronko, M. Lee, J. Blais, D. Cho, S. Chamberland, T. Renau, R. Leger, S. Hecker, W. Watkins, K. Hoshino, H. Ishida and V. J. Lee, “Identification and Characterization of Inhibitors of Multidrug Resistance Efflux Pumps in Pseudomonas aeruginosa: Novel Agents for Combination Therapy,” Antimicrobial Agents and Chemotherapy, Vol. 45, No. 1, 2001, pp. 105-116. doi:10.1128/AAC.45.1.105-116.2001
- H. Nikaido and H. I. Zgurskaya, “AcrAB and Related Multidrug Efflux Pumps of Escherichia coli,” Journal of Molecular Microbiology and Biotechnology, Vol. 3, No. 2, 2001, pp. 215-218.
- F. Van Bambeke, Y. Glupczynski, P. Plésiat, J. C. Pechère and P. M. Tulkens, “Antibiotic Efflux Pumps in Prokaryotic Cells: Occurrence, Impact on Resistance and Strategies for the Future of Antimicrobial Therapy,” Journal of Antimicrobial Chemotherapy, Vol. 51, No. 5, 2003, pp. 1055-1065. doi:10.1093/jac/dkg224
- W. J. Gooderham and R. E. Hancock, “Regulation of Virulence and Antibiotic Resistance by Two-Component Regulatory Systems in Pseudomonas aeruginosa,” FEMS Microbiology Reviews, Vol. 33, No. 2, 2009, pp. 279-294. doi:10.1111/j.1574-6976.2008.00135.x
- K. Nishino, E. Nikaido and A. Yamaguchi, “Regulation and Physiological Function of Multidrug Efflux Pumps in Escherichia coli and Salmonella,” Biochimica et Biophysica Acta, Vol. 1794, No. 5, 2009, pp. 834-843.
- L. Sandegren and D. I. Andersson, “Bacterial Gene Amplification: Implications for the Evolution of Antibiotic Resistance,” Nature Reviews Microbiology, Vol. 7, No. 8, 2009, pp. 578-588. doi:10.1038/nrmicro2174
- J. L. Martinez, A. Fajardo, L. Garmendia, A. Hernandez, J. F. Linares, L. Martínez-Solano and M. B. Sánchez, “A Global View of Antibiotic Resistance,” FEMS Microbiology Reviews, Vol. 33, No. 1, 2009, pp. 44-65. doi:10.1111/j.1574-6976.2008.00142.x
- M. Martins, S. G. Dastidar, S. Fanning, J. E. Kristiansen, J. Molnar, J. M. Pagès, Z. Schelz, G. Spengler, M. Viveiros and L. Amaral, “Potential Role of Non-Antibiotics (Helper Compounds) in the Treatment of Multidrug-Resistant Gram-Negative Infections: Mechanisms for Their Direct and Indirect Activities,” International Journal of Antimicrobial Agents, Vol. 31, No. 3, 2008, pp. 198-208. doi:10.1016/j.ijantimicag.2007.10.025
- J. E. Kristiansen, O. Sebbesen, N. Frimodt-Møller, T. Aaes-Jørgensen and E. F. Hvidberg, “Synergy between a Non-Neuroleptic Thioxanthene Stereo-Isomer and Penicillin in Vivo,” Acta Pathologica, Microbiologica et Immunologica Scandinavica, Vol. 96, No. 12, 1988, pp. 1079-1084. doi:10.1111/j.1699-0463.1988.tb00984.x
- J. Molnár, I. Haszon, T. Bodrogi, E. Martonyi, and S. Turi, “Synergistic Effect of Promethazine with Gentamycin in Frequently Recurring Pyelonephrotis,” International Urology and Nephrology, Vol. 22, No. 5, 1990, pp. 405-411. doi:10.1007/BF02549770
- J. M. Bolla, S. Alibert-Franco, J. Handzlik, J. Chevalier, A. Mahamoud, G. Boyer, K. Kiec-Kononowicz and J.-M. Pages, “Strategies for Bypassing the Membrane Barrier in Multidrug Resistant Gram-Negative Bacteria,” FEBS Letters, Vol. 585, No. 11, 2011, pp. 1682-1690. doi:10.1016/j.febslet.2011.04.054

