American Journal of Analytical Chemistry
Vol.09 No.08(2018), Article ID:86460,13 pages
10.4236/ajac.2018.98028
Quantization Heat Capacity Equations at Constant Volume According to Energy Levels and Planck Constant
Daekyoum Kim1, Youngpak Lee2
1Chemical Engineering Department, Hanyang University, Seoul, South Korea
2Physics Department, Hanyang University, Seoul, South Korea
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 12, 2018; Accepted: July 31, 2018; Published: August 3, 2018
ABSTRACT
The quantization thermal excitation isotherms based on the maximum triad spin number (G) of each energy level for metal cluster were derived as a function of temperature by expanding the binomial theorems according to energy levels. From them the quantized geometric mean heat capacity equations are expressed in sequence. Among them the five quantized geometric heat capacity equations, fit the best to the experimental heat capacity data of metal atoms at constant pressure. In the derivations we assume that the triad spin composed of an electron, its proton and its neutron in a metal cluster become a basic unit of thermal excitation. Boltzmann constant (kB) is found to be an average specific heat of an energy level in a metal cluster. And then the constant (kK) is found to be an average specific heat of a photon in a metal cluster. The core triad spin made of free neutrons may exist as the second one additional energy level. The energy levels are grouped according to the forms of four spins throughout two axes. Planck constant is theoretically obtained with the ratio of the internal energy of metal (U) to total isotherm number (N) through Equipartition theorem.
Keywords:
Statistical Thermodynamics, Quantized Heat Capacity of Metal, Five Energy Levels, Binomial Theorem, Boltzmann Constants, Planck Constant

1. Introduction
The advanced quantized adsorption isotherms derived in the paper [1] fit well to the experimental data which BET isotherm does not fit. Using this total isotherm we can manage to quantize the excited particles number in setting up the total quantized excitation isotherm. We would like to look up the effects of quantization. Several years ago we derived heat capacity equation without quantization [2] . Then five geometric mean heat capacity equations are optimized best. After then quantization form of heat capacity was derived a little in image study [3] . And we have realized that the total quantized excitation isotherm is needed to analyze Planck constant.
The triad spin made of an electron, its proton and its neutron make the harmonic resonances [4] like Figure 1. In another way the excitation means that the metal photon energy of metals is transferred to the measurement gas and the de-excitation means that the metal photon energy of quantized triad spin grossly reverses measurement gas.
2. Statistical Modeling
2.1. Binomial Theorem Model
The general m quantized equation of the binomial expanding for one is
Suppose that since metals can be applied to the generally known electronic configurations, they have the consistent spin models as shown in Figure 2 [2] . Since only the numbers of electrons according to energy levels in a cluster are counted in statistics, the spatial arrangement triad spins in a cluster or the spatial arrangement of particles in a triad spin is immaterial. The orbital protons combine with the negative parts of the orbital neutrons and the orbital electrons in the outside of the metal atom. When a triad spin excites, the particles (an electron, its proton and its neutron) in the triad spin excite dependently and simultaneously, making photons as showed in Figure 1. This figure predicts the disclosure of the coming Figure 3.
Each energy level has one binomial theorem [5] . Since the excitation energies among levels are different, the summation intervals are also different. The maximum number of the un-excited triad spin for each level is for a metal atom. Here Z is the atomic number of the metal and n the number of energy
Figure 1. Three resonance (photons) in interferences of the triad.
Figure 2. The thermal unexcitation and excitation models of electron, protons and neutrons in a pseudo metal cluster.
Figure 3. The electromagnetic wave as photons containing neutrons and 5 energy lines per particles (protons or electrons).
levels. The summation becomes unity according to the mathematics of binomial theorem.
The number of a triad spin excited with the lowest energy is . The lowest energy level has the excitation probability of and the de-excitation probability of . In the above and are the decay constant and the excitation energy of a triad spin with the lowest excitation energy level. The binomial theorem [5] of the lowest energy level becomes
(1)
where
(1.1)
If we have the probability function for the excited a triad spins of the second to nth energy levels and the probability function for the de-excited a triad spins binomial theorems become for
(2)
where
(2.1)
Let us multiply Equation (1) and Equation (2) side by side. Then we get
In the above equation the largest term dominates the probability function. Hence using that the total differential equation should be zero so that
(3)
where
(3.1)
In Equation (2) and are the decay constant and the excitation energy of a triad spins from the second to nth energy levels. But since all equations in the first to nth binomial theorems are dependent on one another, they are multiplied to meet the excitation of triad spins in metal cluster. is smaller than .
Since each excited triad spin is furnished with the same amount of energy (at the same temperature) irrespective of the energy levels, the total excitation (internal) energy U for all excited triad spins becomes
(4)
In Equation (4) is the average excitation energy of triad spins. It is considered that the largest term in Equation (3) dominates the probability function.
Hence by using Srirling’s approximation, we obtain for as follows
(5)
where
(5.1)
for (5.2)
And by using the equations of , and we obtain
(6)
Equation (3) and Equation (4) being introduced into the combined thermodynamics 1st and 2nd law equation, which becomes at the constant volume of the system, the chemical potential of an excited cluster becomes
(7)
The chemical potential of an unexcited cluster may be generally defined as
(8)
Here, the ideal gas relationship for the de-excited cluster with excited cluster is accomplished since Equation (8) can be obtained from Equation (9) in the literature [6] by plugging [7] [8] . The excitation of a triad spin is equal to one excitation of a gas molecule. Since the excitation is measured at the equilibrium between the excited cluster and the de-excited cluster, that is, , by equating Equation (7) to Equation (8) and defining the saturation excitation temperature factor, , we obtain
(9)
where
(9.1)
(9.2)
In Equation (9.2) and are the numbers of triad spins excited of and nth levels at the saturation excitation temperature ( ). After Equations (5) and (6) being added side by side and by introducing Equation (9) into their resulting equations, we obtain
, (10)
where
(10.1)
Equation (10) is the same type equation as the surface adsorption isotherm of the gas molecules adsorbed on the general adsorbent [1] , but they are different each other a little. Here it represents the number of the thermally excited triad spins of the lowest energy level of G. In Equation (10) since each level of a metal atom contains triad spins, G becomes triad spins for one mole of metal atoms (NA = Avogadro number). When three particles in a triad spin make three photons, the heaviest neutron among them may make the motion independently. Hence by substituting instead of G into Equation (10), and multiplying (a specific heat of photons in an average triad spin of a metal atom) and 3 for three photons of triad spins we get
, (11)
By substituting instead of into Equation (11) we can get the heat capacity, of the lowest energy level of a metal cluster at constant volume as follows
, (12)
In Equation (12), is the universal gas constant. In the above equations the subscript 1 represents the lowest energy level. The latter agrees with ours a little. By introducing Equation (10) into Equation (5) and Equation (6) and rearranging after multiplying side by side, the number, of the excited triad spins of the nth energy level is obtained as follows
, (13)
For the heat capacities of the other energy levels at constant volume we use Equations (5), (6), (10) and (13). Hence the heat capacities of the next higher energy levels for and of the excited triad spins in a metal cluster at constant volume become
, (14.1)
, (14.2)
, (14.3)
, (14.4)
, (14.5)
where
, (14.6)
At , the number of heat capacity equations becomes infinitive. The heat capacities can not be added with one another.
and etc. are multiplicative thermodynamic probability (isotherm) functions of energy levels 2, 3 and etc. And so we take the geometric mean heat capacity equations of the above two or three equations and etc. as follow
(15.1)
(15.2)
(15.3)
(15.4)
(15.5)
The geometric mean heat capacity illustrates that the concept of the particles and their collisions for the heat capacity of the metal are counted in the cluster.
Equation (5) and Equation (6) being combined with Equation (10) and Equation (13), the excitation isotherm equation of the total triad spins in a cluster, 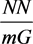 from Equation (16) in the paper [2] is obtained as follows
from Equation (16) in the paper [2] is obtained as follows
(16)
Here let us bring Equation (12) in the paper [1] which is not right, and then let us correct as follows, since it is necessary to infer the coming equation (18).
(17)
where
, (17.1)
By using Equation (17), Equation (16) becomes
, (18)
where in the above
, (18.1)
In the above Equation (16) is accomplished thermodynamically.
2.2. Planck Constant
We calculated the Planck constant according to temperatures by using the equation, [Js/cycle] obtained by equating total internal energy of a metal which can be obtained by the numerical integration of Equation (15.4) with Equation (17.1), quantized heat capacity equation of five energy level, to the total energy of the measurement gas obtained by multiplying NA and NN into the combined equation, of the Equipartition theorem, [8] and the constant [cmK/cycle. In the above the internal energy of metal should use the thermodynamic temperature ( )
Here, the terminology of the excitation isotherm can be used by being based on the saturation excitation temperature (inflection point in heat capacity equation), Ts. In Equation (16) the total isotherm equation is a linear function of z with the unknown variables, and . Hence it can be obtained arithmetically.
3. Results and Discussion
We tried to look over the fitting extent of the theoretically quantized heat capacity equations to the experimental heat capacity data of Ag [9] , Cu [10] , B [11] , Ni [12] [13] , Pd [14] [15] , Pt [16] , Al [10] and Li [17] at the constant pressure by calculating the standard error( ). In all figures A means the constant in the semi-empirical equation, . A of boron is negative. It means in the paper [7] (Table 1).
Equations in paper [7] were calculated by Fortran. Those of this paper are calculated by C(C++) language. Quantization should make the standard errors of this paper.
For all metals we obtained the constant parameters and standard error by
Table 1. Parameter values and (standard error) value obtained by fitting Equation (15.4) ( ) to experimental heat capacity data of metals at the constant pressure.
optimizing the above theoretical heat equation (Equation 15.4) by trial error method through the semi-empirical equation to the experimental heat capacity data at constant pressure. As we see in Figure 2, the five energy lines correspond to five energy resonances including neutrons surrounding and speeding one vacuum wave line. Each proton has five energy lines and each electron also five energy lines. Five energy lines have the relationship with geometric mean equation fit best to the experimental heat capacity at constant pressure. The electromagnetic wave line seems to touch resonances photons lightest. The neutrons aid the electromagnetic wave line get speed.
4.18 = (conversion factor (cal®joule)): (energy level): Tmax (equipartition maximum temperature): (quantization number):
(thermodynamic function ratio between low and higher energy levels) lt (low temperature for integration): ht (high temperature of integration): (testing function); (speed of light ); (Avogadro number);
Generally the used Planck constant {6.625 ´ 10−4 h/Js} are in 900 K of Table 2(a) Instead of this we may use {8.286 ´ 10−33 h/Js} in 900 K of Table 2(b).
Figure 2 is 5 energy lines per electron or proton. They draw a large ellipse. The neutrons charge the electrons and protons n: This value is the number of energy lines required to satisfy the heat capacity. Even if they are fractional numbers, all heat capacity equations are satisfied.
The general text books say that there are two kinds of the spins, the upward spin and the downward spin for the electrons and the upward spin and the downward spin for the proton (+neutrons) in an atom. To discern the spins upward and downward is the same as to discern left and right and forward and backward. Since the metals have the three dimensional structures, it is not reasonable to discern and arrange the spins one dimensionally whether they
Table 2. Planck consts obtained from using parameter values fitting Equation (15.4) ( ) to experimental heat capacity data of metals at the constant pressure. (a) Saturation temperature = 1 K (Inflection point of silver heat capacity); (b) Saturation temperature = 12.5 K (Inflection point of silver heat capacity) with the constants of above a except for inflection point.
are electrons or protons (+neutrons). In the present study we have assumed that the metal atoms have the sphere forms. It is because then metals are crystallized with the consistent spins of the particles. Therefore we can discern electrons and protons (+neutron) respectively have two kinds of spins, and (outward) and and (inward) toward core of sphere. Hence we believe that all metal atoms are made of 4 kinds of orbital spin including their orbital neutrons and other scant one kind of spins made of the free neutrons as mentioned in the modeling. We call the latter the core spin. was the pressure which is . is also θDs satisfy the continuum theory as mentioned in the introduction [5] . The temperature when . is the chemical potential at the certain basic point.
4. Conclusion
The most promising quantized heat capacity equation for metal clusters at the constant volume is . In order to meet this equation we suggest that the spin forms of the five energy levels in metal clusters include neutrons. Then vacant wave is speeded up by photons made of proton and electron with neutrons. But photons do not touch wave line. We can get Planck constant of 6.6256 ´ 10−34 Js at one of the saturation temperatures. But when the saturation temperature is 12.5, the Planck constant becomes 8.286 ´ 10−33 Js. As Quantization is linear, all equations are linear.
Acknowledgements
The author thanks for the encouragements of Yongduk Kim, an emeritus professor of Sogang University. The author also thanks Yu Fang for some modification.
Cite this paper
Kim, D. and Lee, Y. (2018) Quantization Heat Capacity Equations at Constant Volume According to Energy Levels and Planck Constant. American Journal of Analytical Chemistry, 9, 353-365. https://doi.org/10.4236/ajac.2018.98028
References
- 1. Kim, D. (2017) Better Refined Adsorption Isotherm than BET Equatkion. American Journal of Analytical Chemistry, 7, 13-21.
- 2. Kim, D., Lee Y. and Kim T.W. (2010) Heat Capacity Equation of Metals at Constant Volume Based on Binomial Theorem Equations and Their Mechanics. New Physics, Sae Mulli (The Korean Physical Society), 60, 729-740.
- 3. Kim, D. and Choi, Y.S. (2011) Brightness of Lena's Image for Various Values by Using Differentials of the Geometric Mean Heat Capacity at Constant Volume. New Physics: Sae Mulli (The Korean Physical Society), 61, 248-255.
- 4. Kim, D. and Ha, B.-H. (2015) Atomic epn(ep) Spin Models and Spectral Lines. American Journal of Analytical Chemistry, 6, 1030-1037. https://doi.org/10.4236/ajac.2015.613098
- 5. Federick, R. (1985) Fundamentals of Statistical and Thermal Physics. McGraw-Hill International Education, New York City.
- 6. Kim, D. (2000) Statistical Condensation Adsorption Isotherms of Gas Molecules Adsorbed on Porous Adsorbents, Surface Monolayer Adsorption Isotherms and Hysteresis Phenomena. Korean Journal of Chemical Engineering, 17, 600-612. https://doi.org/10.1007/BF02707174
- 7. Eldon, K. (1966) Introduction to STATISTICAL THERMODYNAMICS. McGraw Hill, New York City.
- 8. Sears, F.W. and Salinger, G.I. (1975) Thermodynics, Kinetics Theory and Statistical Thermodynamics. 264-370.
- 9. Meads, P.F., Forsythe, W.R. and Giauque, W.F. (1941) The Heat Capacities and Entropies of Silver and Lead from 15 to 300 K. Journal of the American Chemical Society, 63, 1902. https://doi.org/10.1021/ja01852a028
- 10. Giauque, W.F. and Meads, P.F. (1941) The Heat Capacities and Entropies of Aluminum and Copper from 15 to 300 K. Journal of the American Chemical Society, 63, 1897. https://doi.org/10.1021/ja01852a027
- 11. Johnston Herrick, L., Hersh Herbert, N. and Kerr Eugene, C. (1951) Low Temperature Heat Capacities of Inorganic Solids. V. The Heat Capacity of Pure Elementary Boron in Both Amorphous and Crystalline Conditions Between 13 and 305 K. Some Free Energies of Formation. Journal of the American Chemical Society, 73, 1112. https://doi.org/10.1021/ja01147a068
- 12. Eucken Von, A. and Werth, H. (1930) Die spezifische Warme einiger Metalle und Metallegierungen bei tiefen Temperaturen. Zeitschrift Fur Anorganische Und Allgemeine Chemie, 188, 152. https://doi.org/10.1002/zaac.19301880115
- 13. Busey, R.H. and Giauque, W.F. (1952) The Heat Capacity of Nickel from 15 to 300 K. Entropy and Energe Functions. Journal of the American Chemical Society, 74, 3157. https://doi.org/10.1021/ja01132a058
- 14. Paul Jr., M. and Aston John, G. (1963) The Thermodynamic Properties of Pure Palladium and Its Alloys with Hydrogen between 30 and 300 K. Journal of the American Chemical Society, 85, 137. https://doi.org/10.1021/ja00885a005
- 15. Pickard, G.L. and Simon, F.E. (1948) The Atomic Heats of Palladium, Sodium and Mercury at Low Temperatures. The Proceedings of the Physical Society, 61, 1. https://doi.org/10.1088/0959-5309/61/1/302
- 16. Clusius Von, K., Losa, C.G. and Franzosini, P. (1957) Ergebnisse der Tieftemperaturforschung. Zeitschrift Fur Naturforschung, 12, 34. https://doi.org/10.1515/zna-1957-0108
- 17. Simon, F. und Swain, R.C. (1935) Untersuchungen Uber die spezifischen Warmen bei tiefen Temperaturen. Zeitschrift für Physikalische Chemie, B28, 189. https://doi.org/10.1515/zpch-1935-2819





