American Journal of Analytical Chemistry
Vol.07 No.10(2016), Article ID:71191,17 pages
10.4236/ajac.2016.710062
Theoretical Analysis of Immobilized Oxidase Enzyme Electrode in the Presence of Two Oxidants
Malinidevi Ramanathan1, Rajendran Lakshmanan1,2*
1Department of Mathematics, The Standard Fireworks Rajaratnam College for Women, Sivakasi, India
2Department of Mathematics, Sethu Institute of Technology, Kariapatti, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 25, 2016; Accepted: October 8, 2016; Published: October 13, 2016
ABSTRACT
In this paper, mathematical model of Martens and Hall (Analytical chemistry 66, 2763-2770 (1994 [1] )) for an immobilized oxidase enzyme electrode is discussed. The model involves the system of non-linear reaction diffusion equations under the steady state conditions. A simple and closed-form of approximate analytical expressions for the concentrations of the immobilization of three enzyme substrates has been derived by solving the system of non-linear reaction diffusion equations using new approach of homotopy perturbation method. Approximate polynomial expres- sion of concentration of substrate, oxygen and oxidized mediator and current was obtained in terms of the Thiele moduli and the small values of parameters Bs, Bo and Bm (normalized surface concentration of substrate, oxygen and oxidized mediator). Furthermore, in this work the numerical simulation of the problem is also reported using Matlab program. An agreement between analytical expressions and numerical results is noted.
Keywords:
Mathematical Modelling, Enzyme Electrodes, Non-linear Reaction, Diffusion Equation, New Homotopy Perturbation Method

1. Introduction
There have been many publications on models for enzyme electrodes. Schulmeister et al. [2] have described models for multilayer and multi enzyme electrodes under diffusion control such that enzyme kinetic are linear. Here the reaction and diffusion system is described by a parabolic differential equation with linear in homogeneities Schul- meister et al. [3] . A model for two substrate enzyme electrode has been developed by Leypoldt and Gough where the non-linear enzyme reaction was taken into account. This model was employed to describe the behavior of a glucose oxidase (Gox) electrode Leypoldt et al. [4] . The transient response of a mediated amperometric enzyme electrode was studied by Bergel and Comtat, employing an implicit finite difference method Bergel et al. [5] . Recently Indira and Rajendran et al. [6] have derived analytical expressions for the concentrations of substrate, oxygen and mediator in an amperometric enzyme electrode. Logambal et al. [7] and Anitha et al. [8] have developed the approximate analytical expressions for steady state concentrations of oxidized mediator, substrate and reduce mediator of an enzyme-membrane electrode by the Adomian decomposition method and Homotopy perturbation method. To our knowledge no simple analytical expressions that describe the concentration of substrate, oxygen and oxidized mediator for various values of the Thiele moduli and the normalized parameters have been derived. In this paper we have derived that analytical expressions corresponding to the concentrations of substrate, oxygen, and oxidized mediator in an oxidase enzyme electrode using new Homotopy perturbation method.
2. Mathematical Formulation of the Boundary Value Problem
The details of the model adopted have been fully described in Mertens and Hall [1] and so we only present a brief summary here. Figure 1 represents the general kinetic reaction scheme of an enzyme membrane electrode geometry Gooding et al. [9]
 (1)
(1)
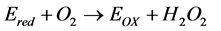 (2)
(2)
 (3)
(3)
We assume that the concentrations of all reactants and enzyme intermediates remain constant for all time. Also the concentration of total active enzyme [Et] and the reactants in the bulk electrode remain constant. We can consider that the diffusion of the reactants can be described by Fick’s second law and the enzymes are assumed to be uniformly dispersed throughout the matrix. The enzyme activity is not a function of position. The coupled three non linear reaction/diffusion equations in normalized form are
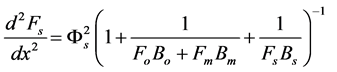 (4)
(4)
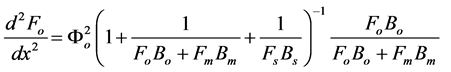 (5)
(5)
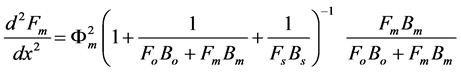 (6)
(6)
The boundary conditions becomes
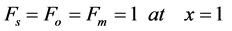 (7)
(7)
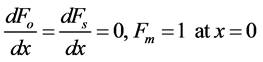 (8)
(8)
Figure 1. Schematic diagram of reaction scheme of an enzyme membrane electrode geometry [8] .
The normalized parameters are
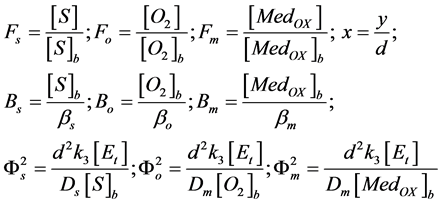 (9)
(9)
where Fs, Fo, and Fm represent the normalized concentrations of substrate, oxygen and oxidized mediator and Bs, Bo, and Bm are the corresponding normalized surface concentrations. The surface concentration is the ratio of the bulk concentration and the reaction constants. Φs, Φo, and Φm denote the Thiele moduli of substrate, oxygen and oxidized mediator, respectively. Thiele modulus Φ2 represents the ratio of the characteristic time of the enzymatic reaction to that of substrate diffusion. d is the thickness of the enzyme layer. The normalized current JOX is given by,
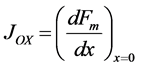 (10)
(10)
3. Analytical Expressions of Concentrations of Substrate, Oxygen and Oxidized Mediator under Steady-State Condition
Recently, many authors have applied the Homotopy perturbation method to solve the various non linear problems in physical and chemical engineering sciences [10] - [12] . This method is a combination of Homotopy in topology and classic perturbation techniques. Ji-Huan He used the HPM to solve the Lighthill equation [13] , the duffing Equation [14] and Blasius Equation [15] . The idea has been used to solve non-linear boundary value problems, integral equations and many other problems [16] - [18] . The HPM is unique in its applicability, accuracy and efficiency. The HPM uses the imbedding parameter  as a small parameter and only a few iterations are needed to find the asymptotic solution with good accuracy. Using the new approach to Homotopy perturbation method, the analytical expressions of steady state concentrations of substrate, oxygen and oxidized mediator (Appendix A) can be obtained as follows:
as a small parameter and only a few iterations are needed to find the asymptotic solution with good accuracy. Using the new approach to Homotopy perturbation method, the analytical expressions of steady state concentrations of substrate, oxygen and oxidized mediator (Appendix A) can be obtained as follows:
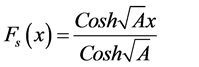 (11)
(11)
 (12)
(12)
 (13)
(13)
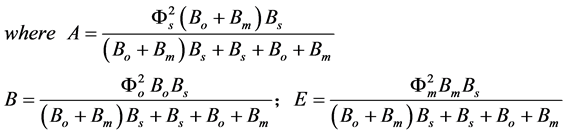
Recently Anitha and Rajendran [8] have derived that analytical expressions corresponding to the concentrations of substrate, oxygen and oxidized mediator in an oxidase enzyme electrode using Homotopy perturbation method. From Equation (10), we can obtain the current as follows:
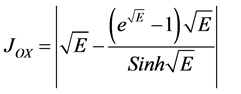 (14)
(14)
Equation (11) to Equation (13) represents the new simple and closed-form of approximate analytical expression of concentrations of substrate, oxygen and oxidized mediator.
4. Discussion
Equation (11) to Equation (13) represent the new closed approximate analytical expression of the non-steady state concentration of substrate, oxygen and oxidized mediator for all values of kinetic and diffusion parameters. The concentration depends on parameters such as Bs, Bo and Bm and Φs, Φo and Φm (Thiele moduli).
Figure 2 shows the dimensionless non-steady state concentration of substrate, oxygen and oxidized mediatorversus dimensionless distance for various values of the dimensionless parameters Bs. From this figure, it is inferred that the concentration of substrate and oxygen decreases when Bs (surface concentration of substrate) increases. Also concentration mediator decreases due to consumption by the enzyme reaction and reaching the minimum at the centre of the membrane (x = 0.5). Then the concentration of the mediator increases from x = 0.5 to x = 1 due reoxidation of the electrode.
Figure 2. (a)-(c): Plot of analytical expression of concentration of substrate oxygen and mediator for various values of parameter Bs using Equations (11)-(13). Dotted line represents numerical solution and solid line represents the analytical solution.
Figure 3 represents the dimensionless non-steady state concentration profiles of substrate, oxygen and mediator for various values of Thiele modulus. Thiele Modulus depends upon thickness of the enzyme layer or amount of enzyme immobilized in the matrix (refer Equation 9). This parameter express the relative importance of diffusion and reaction in the enzyme layer when it is small, kinetics are the dominant and when Thiele modlus is large internal diffusion usually limits the overall rate of reaction. From this figure, we can observed that, the concentration of substrate, oxygen and mediator increases when Thiele modulus decreases. For small values of Thiele modulus, the reaction rate is small compared to the diffusion rate and the concentration becomes nearly uniform. Also the minimum values of the mediator is zero for the large value of Thiele modulus. Concentration is uniform for very small values of Thiele modules (Φi less than 0.1).
Figure 4 represents the concentration of substrate, oxygen and mediator verse the normalized distance for various values Bo. From this figure, it is inferred that the concentrate of substrate and oxygen increases when Bs decreases and become uniform for very small values of Bo. Here also concentration mediator decreases slowly from x = 0 to x = 0.5. Then from x = 0.5 to x = 1 the concentration increases due to reoxidation at the electrode.
Figure 3. (a)-(c): Plot of concentration of substrate oxygen and mediator for various values of parameter


Figure 5 represents normalized current density Jox verses Thiele modules/Bo for various values of dimensionless parameter Bs, Bo, Bm and Φm. From this figure it is observed that, the current density increases when Bs, Bo, Bm (surface concentration of substrate, oxygen, mediator) decreases. The most accessible parameters in the design of a sensor are the thickness of the membrane and the actual loading of active enzyme in the matrix. Also the maximum current decreases with decreases of membrane thickness or actual loading of active enzymes due to decrease in the total amount of enzyme presence in the system.
Tables 1-3 represent the comparison of analytical expression of concentration of the substrate, oxygen and mediator (Fs, Fo, Fm) for various of Thiele modules. The maximum average relative error between the analytical results and numerical results is 1.62%. This error is less than pervious published analytical result [8] .
5. Conclusion
In this paper, steady state nonlinear differential equations in biofiltration model have been solved analytically. Approximate analytical expressions pertaining to the concentrations of substrate, oxygen and oxidized mediator are derived using homotopy perturbation method. These analytical solutions are compared with the numerical simulation results. These analytical results provide a good understanding of the system and
Figure 4. (a)-(c): Plot of concentration of substrate oxygen and mediator for various values of parameter, B0 using Equations (11)-(13). Dotted line represents numerical simulation and solid line represents the analytical expression.
Figure 5. (a)-(d): Normalized current density Jox verses the lie Modules/Bo for various values of the parameters using Equation (14).
Table 1.Comparison of normalized substrate concentration Fs with the numerical result for various of Φs2 and some fixed values of normalized parameters bs=0.04,bo=2.5 and bm=0.2.
Table 2.Comparison of normalized oxygen concentration Fo with the numerical result for various of Φo2 and some fixed values of normalized parameters bs=0.04,bo=2.5 and bm=0.2.
Table 3.Comparison of normalized mediator concentration Fm with the numerical result for various of Φo2 and some fixed values of normalized parameters bs=0.07,bo=2.5 and bm=0.2.
the optimization of the parameters in enzyme model. The extension of the prodecure to other immobilized oxidase enzyme electrode systems at steady and non-steady state condition seems possible.
Cite this paper
Ramanathan, M. and Lakshmanan, R. (2016) Theoretical Ana- lysis of Immobilized Oxidase Enzyme Electrode in the Presence of Two Oxidants. American Journal of Analytical Chemistry, 7, 679-695. http://dx.doi.org/10.4236/ajac.2016.710062
References
- 1. Martens, N. and Hall, E.A.H. (1994) Model for an Immobilized Oxidase Enzyme Electrode in the Presence of Two Oxidants. Analytical Chemistry, 66, 2763-2770.
- 2. Schulmeister, T. (1990) Mathematical Modeling of the Dynamic Behaviour of Amperometric Enzyme Electrodes. Selective Electrode Reviews, 12, 203-260.
- 3. Schulmeister, Th. and Pfeiffer, D. (1993) Mathematical Modelling of Amperometric with Perforated Membranes. Biosensors and Bioelectronics, 8, 75-79.
http://dx.doi.org/10.1016/0956-5663(93)80055-T - 4. Leypoldt, J.K. and Gough, D.A. (1984) Model of a Two-Substrate Enzyme Electrode for Glucose. Analytical Chemistry, 56, 2896-2904.
http://dx.doi.org/10.1021/ac00278a063 - 5. Bergel, A. and Comtat, M. (1984) Theoretical Evaluation of Transient Responses of an Amperometric Enzyme Electrode. Analytical Chemistry, 56, 2904-2909.
http://dx.doi.org/10.1021/ac00278a064 - 6. Indira, K. and Rajendran, L. (2013) Analytical Expressions for the Concentrations of Substrate, Oxygen and Mediator in an Amperometric Enzyme Electrode. Applied Mathematical Modelling, 37, 5343-5358.
http://dx.doi.org/10.1016/j.apm.2012.10.021 - 7. Shumugham, L. and Rajendran, L. (2013) Analytical Expressions for Steady-State Concentrations of Substrate and Oxidized and Reduced Mediator in an Amperometric Biosensor. International Journal of Electrochemistry, Article ID: 812856, 12 p.
- 8. Shanmugarajan, A. and Lakshmanan, R. (2012) A Theoretical Model for an Immobilized Oxidase Enzyme Electrode in the Presence of Two Oxidants. Journal of Modern Mathematics Frontier, 1, 46-56.
- 9. Gooding, J.J. and Hall, E.A.H. (1996) Practical Evaluation of an Alternative Geometry Enzyme Electrode. Journal of Electroanalytical Chemistry, 417, 25-33.
http://dx.doi.org/10.1016/S0022-0728(96)04752-3 - 10. Li, S.J. and Liu, Y.X. (2006) An Improved Approach to Nonlinear DynamicalSystem Identification Using PID Neural Networks. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 177-182.
- 11. Mousa, M.M., Ragab, S.F. and Nturforsch, Z. (2008) Application of the Homotopy Perturbation Method to Linear and Nonlinear Schrodinger Equations. Zeitschriftfür Naturforschung, 63, 140-144.
- 12. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262.
http://dx.doi.org/10.1016/S0045-7825(99)00018-3 - 13. He, J.H. (2003) Homotopy Perturbation Method: A New Nonlinear Analytical Technique. Applied Mathematics and Computation, 135, 73-79.
http://dx.doi.org/10.1016/S0096-3003(01)00312-5 - 14. He, J.H. (2006) Some Asymptotic Methods for Strongly Nonlinear Equations. International Journal of Modern Physics B, 20, 1141–1199.
http://dx.doi.org/10.1142/S0217979206033796 - 15. He, J.H., Wu, G.C. and Austin, F. (2009) The Variational Iteration Method Which Should Be Followed. Nonlinear Science Letter A, 1, 1-30.
- 16. He, J.-H. (2003) A Simple Perturbation Approach to Blasius Equation. Applied Mathematics and Computations, 140, 217-222.
- 17. He, J.-H. (2000) A Coupling Method of a Homotopy Technique and a Perturbation Technique for Non-Linear problems. International Journal of Non-Linear Mechanics, 35, 37-43.
- 18. Ganji, D.D., Amini, M. and Kolahdoo, A. (2008) Analytical Investigation of Hyperbolic Equations via He’s Methods. American Journal of Engineering and Applied Science, 1, 399-407.
Nomenclature
Symbols:
Greek symbols:
Appendix: A
Approximate Analytical Solution of Equations (4)-(6) Using New Approach of Homotopy Perturbation Method.
Here, we have indicated how to obtain the solution of Equations (4)-(6) using the initial and boundary conditions Equation (7) & Equation (8). We consider the following non-linear differential equation.

where L is a linear operator, N is a non-linear operator, u is an unknown function, and f (r) is a given continuous function. We construct a homotopy which satisfies.

Here p [0, 1] is an embedded parameter. Using the above Equation (A2), we can construct the homotopy [8] for the Equations (4)-(6), as follows:



Supposing the approximate solutions of Equations (4)-(6) have the form

Substituting Equation (A6) into Equations (A3)-(A5) (respectively), and equate the terms with the identical powers of p, we obtain.



The above equations can be written as



The initial approximations boundary conditions Equation (7) and Equation (8) are as follows.


And


Solving the Equations (A7)-(A9) and using the boundary conditions Equation (A13) and Equation (A14) we get



where
Using the basic assumptions underlying the homotopy method, we obtain since the



value of the first order iteration 
Appendix: B
Matlab Program to Find the Numerical Solution of Equations (4)-(6) functionpdex4
m = 0;
x = linspace (0,0.5);
t = linspace (0,100);
sol = pdepe (m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
u2 = sol(:,:,2);
u3 = sol(:,:,3);
figure
plot(x,u1(end,:))
xlabel('Distance x')
ylabel('u1(x,2)')
figure
plot(x,u2(end,:))
xlabel('Distance x')
ylabel('u2(x,2)')
figure
plot(x,u3(end,:))
xlabel('Distance x')
ylabel('u3(x,2)')
% --------------------------------------------------------------
function [c,f,s] = pdex4pde(x,t,u,DuDx)
Bs=0.5;
Bo=0.05;
Bm=0.1;
A=0.1;
J=0.1;
E=0.1;
c = [1;1;1];
f = [1;1;1].* DuDx;
F1 =-A/(1+1/(u(2)*Bo+u(3)*Bm)+1/(u(1)*Bs));
F2 =-J/(1+1/(u(2)*Bo+u(3)*Bm)+1/(u(1)*Bs))*(u(2)*Bo/(u(2)*Bo+u(3)*Bm));
F3 =-E/(1+1/(u(2)*Bo+u(3)*Bm)+1/(u(1)*Bs))*(u(3)*Bm/(u(2)*Bo+u(3)*Bm));
s = [F1; F2; F3];
% --------------------------------------------------------------
functionu0 = pdex4ic(x)
u0 = [0; 0; 1];
% --------------------------------------------------------------
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
pl = [0; 0 ; ul(3)-1];
ql = [1; 1 ; 0];
pr = [ur(1)-1; ur(2)-1 ; ur(3)-1];
qr = [0; 0; 0];
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact ajac@scirp.org













