American Journal of Analytical Chemistry
Vol.5 No.10(2014), Article ID:47887,13 pages
DOI:10.4236/ajac.2014.510071
Quantitative Analysis of Lavender (Lavandula angustifolia) Essential Oil Using Multiblock Data from Infrared Spectroscopy
Nathalie Dupuy, Vincent Gaydou, Jacky Kister
Aix Marseille University, LISA, METICA, EA4672, F-13397 Marseille 20, France
Email: nathalie.dupuy@univ-amu.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2014; revised 14 June 2014; accepted 26 June 2014
ABSTRACT
Near-infrared and mid-infrared spectroscopies were currently used to analyze natural compounds. During the last ten years various multiblocks methods were developed such as Concatenated PLS, Hierarchical-PLS (H-PLS), and MultiBlock-PLS (MB-PLS). These three algorithms were used to analyze 55 lavender (Lavandula angustifolia) essential oil samples. The results obtained were compared to the ones obtained respectively in NIR and MIR ranges. The accuracies of the models depend on the spectroscopic technique, pretreatment and the PLS methods. The results showed that the choice of the factor numbers used to build the multiblock models was the most important parameter for the H-PLS and MB-PLS methods.
Keywords: Multiblock Regression, Lavandula angustifolia, Lavender Essential Oil, NIR, MIR, H-PLS, MB-PLS

1. Introduction
Vibrational spectroscopies such as NIR and MIR, when associated to multivariate analysis, have been proved to be a powerful tool in various product analyses like gasoline samples [1] , diesels [2] , fuel [3] [4] , olive oils [5] [6] or lavandin essential oils [7] . These analytical spectroscopic methods, besides being shorter in time than the usual ones (ASTM methods), present good accuracy and precision; are non-destructive; and can be used for quality control. During the last decade, a lot of progress appeared in the analytic world. The time necessary to obtain analytic data decreases, so for one manufactured product, multiple measurements are done (NIR, MIR spectroscopies, liquid or gas chromatography, sensorial analysis). The data are considered as independents; the NIR or MIR data could be used to quantify compounds by using regression methods as Partial Least Square (PLS) regression. Each group of variables, or each matrix, is usually called a block and is measured on the same observations (in rows). It is possible to find complementary information using two different analytic methods. In this case the analyst could use multiples predictors blocks and multiblocks responses blocks. In the literature several multiblocks methods were described [8] . The first method called concatenated method consists in concatenating the descriptor block into the same matrix and then applying Partial Least Square (PLS) regression. Sometimes this method works well, but the individual blocks must be scaled to obtain interpretable results. The second method consists in considering each block independently at the beginning. Principal Component Analysis (PCA) could be applied on each block and then the scores obtained in each block are collected together to form a super matrix. The PLS regression is then applied on the super matrix. This method presented by Tenenhaus and Vinzi [9] is called Hierarchical-PLS (H-PLS). The third method is proposed by Wangen and Kowalski [10] , the PLS regression is applied on each block and then the scores obtained in each block are collected together to form a super matrix. The PLS regression is then applied on the super matrix. This whole process is called MultiBlockPLS (MB-PLS). The objective of this study is to realize the determination of the five main compounds which compose the lavender (Lavandula angustifolia) essential oil, using multiblock chemometric methods. This plant, native from the Mediterranean Basin, is widely cultivated for essential oil production. Pure L. angustifolia essential oils are used in perfumery, cosmetic, for antimicrobial activity, and anti-colic properties [11] . These oils are characterized by high level of linalool and linalyl acetate, moderate levels of lavandulyl acetate, terpen-4-ol and lavandulol. The amount of 1,8-cineole and camphor often vary between very low to moderate [12] . In this work, five compounds of lavender’s essential oil were quantified by each chemometric method and these methods were compared. Four chemometric methods have been used to build the regression models: PLS method was used independently on NIR and MIR data, and three multiblock methods (concatenated, H-PLS and MBPLS methods) were applied on NIR and MIR data in a simultaneous way.
2. Experimental
2.1. Essential Oil Samples
The lavender (Lavandula angustifolia) essential oils investigated in this work were provided by the Office National Interprofessionnel des Plantes à Parfum, Aromatiques et Médicinales (ONIPPAM) and they belong to the label “AOC Huiles essentielles de Lavande de Haute-Provence” (Origin Protected Designation of “Haute-Provence”). The oils were obtained by vapor phase distillation of the flowery part recently cut, of the L. angustifolia species, spontaneous growing or cultivated in south of France. The samples were left in two groups, including a group of calibration (42 samples) and a group of validation (13 samples). The samples with the minimum and maximum contents for each compound investigated were added in calibration set. The other samples were randomly selected between prediction and calibration set.
2.2. Gas Chromatography
The composition of the 55 lavender essential oil samples, was determined by internal normalization using an Agilent 7890A GC System, equipped with a capillary column SUPELCOWAX 10 of 30 m (DI: 25 µm, phase thickness: 0.25 µm), a FID detector, dihydrogen as gas vector, and following the analysis protocol established by the French National Association for Normalization (AFNOR) [13] . The mean composition was done in the Table1
2.3. FT-NIR
FT-NIR spectra were recorded with a Nicolet Antaris spectrometer interfaced to a personal computer. Samples were filled into glass tubes of 2 mm. All spectra were computed at 8 cm−1 resolution between 4000 and 10,000 cm−1, thanks to the software result integration 2.1 Thermo Nicolet. Co-addition of symmetrical interferograms on 100 scans was performed for each spectrum. A reference spectrum and sample spectrum was recorded with glass tubes of 2 mm.
2.4. FT-MIR
FT-MIR spectra were recorded with a Thermo Nicolet AVATAR 370 spectrometer interfaced to a personal computer. Samples were deposed on an Attenuated Total Reflectance (ATR) accessory. All spectra were com
Table 1. Products identified by GC.
puted at 2 cm−1 resolution between 700 and 4000 cm−1. Co-addition of symmetrical interferograms on 100 scans was performed for each spectrum. A reference spectrum was recorded before each sample spectrum.
2.5. Software
The chemometric applications were performed by the UNSCRAMBLER software Version 9.2 from CAMO (Computer Aided Modelling, Trondheim, Norway) and by the MATLAB software Version 7.4 from The Math Works Inc. (Natick, Units States).
3. Chemometric Methods
3.1. Partial Component Analysis (PCA)
Principal component analysis [14] involves a mathematical procedure that transforms a number of possibly correlated variables into a smaller number of uncorrelated variables called principal components. The first principal component accounts for as much of the variability in the data as possible, and each succeeding component accounts for as much of the remaining variability as possible. Data sets with many variables can be simplified through variable reduction and thereby be more easily interpreted.
3.2. Partial Least Square (PLS) Regression
PLS is a supervised analysis that is based on the relation between the signal intensity and the characteristics of the sample [15] . Interference and overlapping of the spectral information may be overcome by using powerful multicomponent analysis such as PLS regression. PLS allows a sophisticated statistical approach using a spectral region rather than unique and isolated analytical bands [16] [17] . The algorithm is based on the ability to mathematically correlate spectral data to a property matrix of interest while simultaneously accounting for all other significant spectral factors that perturb the spectrum. It is thus a multivariate regression method that uses a selected spectral region and is based on the use of latent variables. To construct a model, the first step is to perform a calibration. This involves collecting a calibration set of reference samples which should contain all chemical and physical variations to be expected in the unknown samples, which will be predicted later. The purpose of this calibration is to establish a multiple linear regression between the NIR spectra data or MIR spectra and the various parameters of the sample set [volatile compounds (water in the majority), lipid rates, or varietal origins]. Cross-validation was applied in regression to fix the required number of latent variables for model construction. So, the optimal number of latent variables is determined on the basis of prediction of samples kept out from the individual model. The second step is to validate the model using a prediction set (different from the calibration one), i.e. to compare the values obtained by the model to the values obtained by the reference method.
The evaluation of the calibration performance is estimated by computing the standard error of calibration (RMSEC) after comparing the real modification with the computed one for each component. The formula for the standard error of calibration is [18] :
 (1)
(1)
where Ci is the known value,
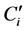 is the calculated value, N is the number of
samples and p is the number of independent variables in the regression.
is the calculated value, N is the number of
samples and p is the number of independent variables in the regression.
The standard error of prediction (RMSEP) gives an estimation of the prediction performance during the step of validation of the calibration equation:
 (2)
(2)
where Ci is the known value,
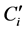 is the value calculated by the calibration
equation, and M is the number of samples in the prediction set.
is the value calculated by the calibration
equation, and M is the number of samples in the prediction set.
The predictive ability of the model should also be expressed by the bias and the square of correlation coefficient (R2) also called determination coefficient, usually called Q2 in prediction. The regression coefficients are the numerical coefficients which express the link between the predictor variations and the response variations. The bias is systematic difference between predicted and measured values. The bias is computed as average value of the residuals. The residual is the measure of the variation which is not taken into account by the model. The residual for a given sample and a given variable is computed as the difference between observed value and fitted (projected or predicted) value of the variable on the sample. For this study, the full cross validation is chosen to validate all models.
3.3. Multiblock Methods
Nowadays, it is possible to arrange, for the same sets of samples, several blocks of analytical variables. These various data sets or these various blocks are obtained by means of various analytical methods, for example data stemming from the spectroscopy NIR and from the spectroscopy MIR. Every block contains information relative to the variance of samples and it was intended to use multiblock methods because. These methods are able to treat all the blocks in a simultaneous way and three multiblock methods were used for this study.
3.4. Concatenated Matrix
Data arrangement [19] for combined-PLS:
X-block: virgin olive oil spectra data have been arranged in two ways by taking NIR and MIR absorbances as columns, yielding the X-matrix (the X-matrix data constituted the independent set of variables).
Y-block: the Y-block data were the set of dependent variables. For combining NIR and MIR spectra, the data were normalized at the unit vector in order to give the same importance for the two spectral regions.
3.5. H-PLS Models
This method presented by Wold et al. [20] was called H-PLS.
Data arrangement:
X-block: PCA of the lavender oil NIR and MIR data have been calculated separately. PCA was performed on the calibration set and the same model was used for the decomposition of the prediction one. The scores of each PCA were extracted in order to build another data matrix named TT.
Y-block: the Y-block data were the set dependent variable.
A PLS cycle [21] is done between TT and each predictor from which a super weight and an updated super score TT are obtained normalized to unit length [22] . These cycles are repeated until TT converged [23] . Evaluation of error for this method is estimated as a classical PLS. The algorithm of the method H-PLS is very clearly presented in the publication of Westerhuis et al. [24] .
3.6. MultiBlock-PLS (S-PLS)
Data arrangement for S-PLS models:
The third way was proposed by Wangen and Kowalski [10] Partial Least Square (PLS) regression was applied on each block and then the scores obtained in each block were collected together to form a super matrix. The PLS regression was then applied on the super matrix. This method was called S-PLS. The main difference between this algorithm and the algorithm of H-PLS is that for the S-PLS, the scores of every block of data are calculated by means of a PLS associated with quantitative information. Then the blocks of scores are concatenated to form the “super block” matrix of and finally a new PLS is realized on this super block matrix. The method of the S-PLS was worked out to treat relations of variance (and of covariance) between several blocks of data. This method is able of taking into account the variances of K blocks of analytical variables and of putting them in connection with several blocks of variables to be explained (quantitative information). The algorithm of the method S-PLS is also clearly presented in the publication of Westerhuis et al. [25] .
X-block: PLS scores of the lavender oil NIR and MIR data have been calculated separately and concatenated.
Y-block: the Y-block data were the set dependent variable.
3.7. Data Pretreatment
Data analysis was carried out using the full spectra. Mean centering was used to improve the smaller spectral differences removing the common information from the spectra. Absorbance normalized value was also employed. None of the other mathematical treatments (multiplicative scatter correction, second derivative [26] , etc.) or wavelength ranges tested improved the prediction accuracy of models. During the data processing, the Standard Normal Variate (SNV) correction pretreatment [27] could be used. The SNV pretreatment is a row-oriented transformation that removes scatter effects from spectra by centering and scaling each individual spectrum. To perform the variable matrices, some pretreatments (or preprocessings) were done. This step is very important to study matrix of spectra. The pretreatments could be combined in order to optimize the models. In this work, influences of pretreatments were compared.
4. Results and Discussion
Compound identification of the lavender samples were done using retention indices and co-elution with authentic samples of the five compounds investigated. The percentages were determined by the method of area normalization and without the application of response factor corrections according to standard methods [25] . The variables to be explain (quantitative content data) were obtained by internal normalization.
In Table 2, the mean and range of the main five compounds, i.e. linalool, lavandulol, linalyl acetate, lavandulyl acetate and ß-caryophyllene are given with both calibration and validation sets according to the targeted compounds. As shown in this table, linalool and linalyl acetate are the main compounds (28.8% and 37.2% respectively for the calibration set). The three other compounds present a range around 5%, in the two sets. The spectroscopic variables from NIR and MIR were used for building chemometrics models using multiblock methods, concatenated block, hierarchical PLS method and MB-PLS method. The efficiently of NIR and MIR ranges were first studied, then the 2 spectral ranges were concatenated, the H-PLS and S-PLS methods were checked. For each of following studies same groups of samples in calibration and in prediction were preserved.
4.1. Near Infrared Studies
Several models of regression were then elaborated with samples of calibration to predict contents in linalool, lavandulol, linalyl acetate, lavandulyl acetate and ß-caryophyllene in the [4500 - 5000 cm−1] and [6000 to 7200 cm−1] spectral ranges. Various pretreatments were tested for each targeted compounds. The pretreatments which allowed obtaining the best regression models were baseline correction followed by SNV for the 5 compounds. The best calibration model characteristics appear in left part of Table3 The number of factors used for each ofthese models of regression varies from 2 to 5 and R2 obtained for linalool (0.99), linalyl acetate (0.99) and la
FN: suggested number of factor used, R2: coefficient of regression, RMSEC: root mean square error of calibration, REC: relative error of calibration, Q2: coefficient of determination, RMSEP: root mean square error of prediction, REP: relative error of prediction.
vandulol (0.92) are close to 1. On the other hand, for lavandulyl acetate and ß-caryophyllene, calculated R2 (0.76 and 0.89 respectively) are low.
The calculated RMSEC is included between 0.161% and 0.254%. These values are relatively close to some of the others and they express the error of prediction realized by the models to predict the compound contents. When the RMSEC is expressed with respect to the average compound content, we calculate the REC which are relative errors and allow more easily comparison models between them. So REC obtained for linalool (0.69%) and linalyl acetate (0.67%) are particularly close to zero (with regard to three other REC) and explain a good quality of prediction of these compounds contents in calibration samples. Then, the five models of regression are validated by means of the validation sample’s set. Q2 obtained are respectively lower than R2 and the RMSEP is respectively higher to RMSEC. The calculated REP translates a good prediction of the linalool content of the validation samples. The REP of the other models presented low prediction qualities in particular for the lavandulol and ß-caryophyllene because the REC obtained for these two compounds are around 10%. We can observe that the validation of the regression model of the lavandulyl acetate is bad because the REP is equal to 4.2% while the REC obtained during the calibration of this model was 0.67%.
4.2. Medium Infrared Studies
With calibration samples set, 5 regression models were then elaborated in the 700 and 1900 cm−1 spectral range to predict contents in linalool, lavandulol, linalyl acetate, lavandulyl acetate and ß-caryophyllene of the calibration set samples. The various pretreatments were tested for each compounds, however the best regression models were obtained without making any pretreatment. The best characteristics of regression models obtained are given in Table 3 which shows that, without any pretreatment, it was possible to elaborate good calibration models. R2 obtained are all very close to one. The RMSEC are very close to zero in comparison with those obtained with the NIR data. The models are then validated and the characteristics of the validation of each regression model are given in Table2 Q2 obtained are respectively lower than R2 in particular for linalyl acetate regression model (0.64 and 0.98 respectively for this compound). The RMSEP are higher to the RMSEC (in particular for the linalyl acetate) and the REP obtained for linalool regression model is particularly successful (REP = 0.91%). Other regression models present relatively small REP (3% and 3.5% respectively for linalyl and lavandulyl acetates; and 7% and 7.5% respectively for lavandulol and ß-caryophyllene). The pretreatments of baseline correction and SNV used with the NIR data allowed to improve regression models, while the MIR data allowed to obtain good qualities of regression models without any pretreatment. On the other hand, factors number used with the MIR data is higher to those used by the NIR data and the REP obtained by means of the MIR data are smaller than those obtained with the NIR data about is the targeted compound. In conclusion, MIR spectroscopy is the most suitable spectroscopic domain. However, it is possible that simultaneous use of these two spectroscopic domains allows elaborating even more precise regression models and it is in this optic that the multiblocks methods were applied.
4.3. Multiblock Method: NIR + MIR Studies
The multiblock method allowed organizing chemical information from NIR and MIR data. Three multiblock methods were compared: the concatenated matrix (CONC) method, the hierarchical PLS (H-PLS) method and the MultiBlock-PLS (MB-PLS) method. All the regression models were elaborated from NIR and MIR data of the calibration sample set. The pretreatments used were baseline correction followed by a SNV on NIR data and no pretreatment on MIR data. The spectral ranges previously determined, were kept for application of multiblock methods.
4.3.1. Study on Concatenated Matrix
The two calibration matrixes sample set were normalized after the pretreatment then the data were concatenated. The calibration model characteristics are presented according to the targeted compound, in Table3 The regression models elaborated for each compound presented good accuracy. Indeed R² are very close to 1 and the RMSEC are close to 0. The calculated REC are thus low. The regression models were then validated with the validation sample set. Q2 are smaller than R2 (for the same compound) in particular for ß-caryophyllene of which R2 is 0.998 while Q2 is 0.69. The obtained RMSEP are significantly higher in relation to RMSEC. The REP obtained for linalyl acetate is particularly interesting because it is lower than the obtained REP (for the same compound) by using only MIR data (3.0% with MIR data and 2.9% with the concatenated matrix method). The bias of validation of each model is relatively low in relation to the mean content of corresponding compound. The Figure 1 presents the first vectors of regression of the five targeted compounds. These regression vectors are expressed according to NIR and MIR spectroscopic variables. The regression coefficients stemming from MIR data are on the left of the dotted line and those stemming from NIR data are positioned to the right of this line. The intensity of the coefficients stemming from MIR data is higher than those outcomes from NIR data. This observation confirms the relevance of the MIR data with regard to the NIR data.
4.3.2. Study on H-PLS
The method of hierarchical PLS (H-PLS) was organized by following the algorithm described by Westerhuis [24] . To estimate the optimal factor number used for the first stage of H-PLS (the PCA stage), a “test set” was
Figure 1. First vector of regression of 5 targeted compounds (CONC).
set up with the calibration samples set. Previously, 42 samples participated in the calibration. 10 of these samples were chosen to constitute the “test set” of H-PLS. Then, by means of 32 remaining calibration samples, 31 regression models of H-PLS were elaborated with a PCA vector score number varying between 1 to 31. The great matrices scores thus obtained present dimensions going from 2 to 62 variables because the number of vectors scores calculated for every block of data is identical. 31 regression models of H-PLS were then validated by means of the “test set”. Figure 2 concerns only linalool content and shows on vertical axis, the RMSEP’s intensity of the test set, in function of 2 variables. The first variable (in-depth axis) is the number of PCA score vector calculated for each block (NIR and MIR block) during the first stage of H-PLS. The second variable (horizontal axis) is the number of PLS score vector calculated during the second stage of H-PLS. This Figure 2 has the shape of a quarter of bowl. When the number of vectors scores is low, the test set’s RMSEP values are high and they exceed the scale of the RMSEP.
However a minimum of test set’s RMSEP is observed. The coordinates of this minimum are registered in the white box on Figure 2. For each compound the number of PCA scores included in the model varied and the best results are obtained for 21 scores for the linalool, 12 scores for the lavandulol, 9 for linalyl acetate, 8 for lavandulyl acetate and 7 for ß-caryophyllene. Then, new regressions models were elaborated by means of 42 calibration samples of calibration set. NIR and MIR data were used in the algorithm of the H-PLS after the variable pretreatments (baseline correction + SNV for NIR data) and by using only the selected spectroscopic variables. For each compound, the optimal number of vector scores calculated by blocks is given in Table4
These numbers were optimized by means of the test set (in this way, the dimension of the H-PLS great matrix scores, is equal to the double of the number of vector scores calculated by block, because two blocks of data are used in this study). The characteristics of the regression models obtained for each targeted compounds are given in Table 4 (in H-PLS part). R2 calculated are close to 1 with the exception of lavandulyl acetate (0.76) and of ß-caryophyllene (0.52). Obtained RMSEC are small with regard to the average contents of targeted compounds (with the exception of ß-caryophyllene). The H-PLS model is then validated with the validation sample set. Characteristics of validation are given in Table3 Q2 concerning the regression model of linalool (0.89) is the closest to one. Q2 for other regression models between 0.8 and 0.3, indicate a relatively bad validation. The ob-

Figure 2. Test set’s RMSEP in function of the number of score calculated for each block (first stage of H-PLS) and in function of regression number vector (second stage of H-PLS) for linalool analysis.
FN: suggested number of factor used, R2: coefficient of regression, RMSEC: root mean square error of calibration, REC: relative error of calibration, Q2: coefficient of determination, RMSEP: root mean square error of prediction, REP: relative error of prediction.
tained REP are also high, particularly for the lavandulol (14.7%) and ß-caryophyllene (24.7%). For the linalool, the first regression vector calculated using the H-PLS method includes 42 variables. These variables correspond to PCA vector scores, normalized and concatenated. These vectors form the super score matrix and it is from this matrix that the regression vectors are calculated. Figure 3 gives a graphic representation of the H-PLS first regression vector of linalool. Variables stemming from vectors score PCA of MIR data is to the left of the dotted line and those outcomes of vectors score PCA of NIR data is positioned to the right. This vector of regression allows observing the weight of vectors scores PCA stemming from MIR and NIR spectroscopic domains. The vectors scores 5 and 13 are the most important concerning the block of MIR data. This report is surprising because it is the first vectors calculated scores which explain the maximum of variance. It thus means that the useful information is scattered in the data and it is not significant towards the general variance of the data. The first vector scores calculated with the block of NIR data is the one which has most importance for this spectral domain.
Figure 3. First vector of regression of linalool (H-PLS).
4.3.3. Study on MultiBlock-PLS
The multiblock PLS (S-PLS) method was organized by following the algorithm described by Westerhuis [24] . As for H-PLS study, the optimal PLS score number calculated, to make the super score matrix, was estimated by means of a “test set” by 10 samples. The 31 supers scores matrixes were built by means of 32 remaining samples of calibration (outside the test set). The dimensions of these matrices are included between 2 and 62. 31 models of regression S-PLS are then validated by means of the test set. However a minimum of test set’s RMSEP is observed. The number of PLS scores calculated for each block was optimized to 9 for the linalool, 3 for the lavandulol, 10 for linalyl acetate, 3 for lavandulyl acetate and for ß-caryophyllene. Then, models of regression are elaborated by means of 42 samples of calibration set. NIR and MIR data were used in the algorithm of the SPLS after the pretreatment. For each compound, the number of vector scores calculated by block is given in Table5
Five regression models were elaborated and the characteristics of these models are given in Table5 Calculated R2 are close to one for linalool and linalyl acetate. Concerning lavandulol and lavandulyl acetate, R2 are respectively equal to 0.73 and 0.70. It indicates that the regression models concerning these two products are of less efficient than the regression models concerning linalool and linalyl acetate. R2 obtained for ß-caryophyllene, is around 0.6 showing a bad regression model. The obtained RMSEC are not small any more with regard to the average content of the targeted compounds. So, the obtained REC are high, in particular for ß-caryophyllene of which the REC is 18%. The S-PLS regression models were validated by validation sample set and the validation characteristics are given in Table5 Q2 obtained are sharply lower than corresponding R2, respectively for each of targeted compounds. The RMSEP are then more brought up than the RMSEC and the obtained REP are thus of less good quality than the REC. For example for the lavandulol, the REC is equal to 12% while the REP is 16%. The model of regression of linalool presented satisfactory characteristics of validation since the REP is 1.95%. The validation characteristics of linalyl and lavandulyl acetate models are less good because the calculated REP for these models is 3.45% and 6.86% respectively. The ß-caryophyllene regression model is bad with a REP higher than 25%.
Figure 4 gives a graphic representation of the first S-PLS regression vector concerning linalool. Regression
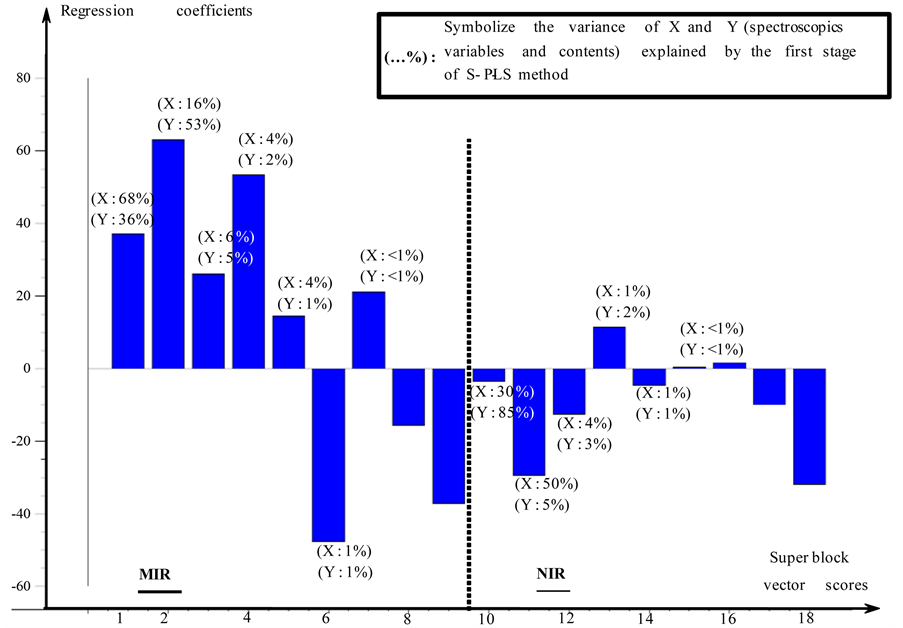
Figure 4. First vector of regression of linalool (S-PLS).
FN: suggested number of factor used, R2: coefficient of regression, RMSEC: root mean square error of calibration, REC: relative error of calibration, Q2: coefficient of determination, RMSEP: root mean square error of prediction, REP: relative error of prediction.
coefficients stemming from vectors score PLS of MIR data are to the left of the dotted line and those stemming from vectors score PLS of NIR data is positioned to the right of this dotted line. The percentages given in brackets indicate the proportion of variance explained. This regression vector allows observing the weight of PLS vector scores stemming from spectroscopic domains. We can notice that it is the first calculated PLS vector scores which have most importance concerning the block of MIR data. Whereas calculated PLS vector scores with the block of NIR data present low intensities in regression coefficient except for vector scores 2 and 9 for the NIR block (vectors scores 11 and 18 on Figure 4). The vector score 18 explain a small proportion of the variance (lower than 1%) but the corresponding regression coefficient has its vector score is brought up. It means that a very low variance influenced strongly the regression.
5. Conclusion
This study on the determination of main compounds of lavender essential oil samples illustrates capacities and limits of the multiblock methods. Although numerous compounds characterized this essential oil, the range content of these last ones is relatively low. From this little variation in composition, chemometric methods allowed elaborating reliable methods of quantification for the five principal compounds contained in these essential oils: linalool, lavandulol, linalyl acetate, lavandulyl acetate and ß-caryophyllene. The affected accuracy is included between 1% for linalool and 8% for ß-caryophyllene. For this study, MIR data were the most adapted data to the implementation of the regression models. The method of concatenated table gave interesting results but other multiblock methods did not show particular capacity.
Acknowledgements
The authors are grateful to the Office National Interprofessionnel des Plantes à Parfum, Aromatiques et Médicinales (ONIPPAM) for providing authentic lavander essential oil samples.
References
- Oliveira, F., Brandao, C., Ramalho, H., da Costa, L., Suarez, P. and Rubim, J. (2007) Adulteration of Diesel/Biodiesel Blends by Vegetable Oil as Determined by Fourier Transform (FT) near Infrared Spectrometry and FT-Raman Spectroscopy. Analytica Chimica Acta, 594, 194-199. http://dx.doi.org/10.1016/j.aca.2007.01.045
- Santos, V., Oliveira, F.C.C.., Lima, D.G., Petry, A.C., Garcia, E., Suarez, P.A.Z. and Rubim, J.C. (2005) A Comparative Study of Diesel Analysis by FTIR, FTNIR and FT-Raman Spectroscopy Using PLS and Artificial Neural Network Analysis. Analytica Chimica Acta, 547, 188-192. http://dx.doi.org/10.1016/j.aca.2005.05.042
- Cooper, J., Larkin, C., Christopher, M., Schmitigal, J., Morris, R. and Abdelkader, M. (2011) Rapid Analysis of Jet Fuel Using a Handheld Near-Infrared (NIR) Analyzer. Applied Spectroscopy, 65, 187-192.http://dx.doi.org/10.1366/10-06076
- Silva, A., Pontes, L., Pimentel, M. and Pontes, M. (2012) Detection of Adulteration in Hydrated Ethyl Alcohol Fuel Using Infrared Spectroscopy and Supervised Pattern Recognition Methods. Talanta, 93, 129-134.http://dx.doi.org/10.1016/j.talanta.2012.01.060
- Casale, M., Casolino, C., Oliveri, P. and Forina, M. (2010) Characterisation of Table Olive Cultivar by NIR Spectroscopy. Food Chemistry, 118, 163-168. http://dx.doi.org/10.1016/j.foodchem.2009.04.091
- Galtier, O., Dupuy, N., Le Dréau, Y., Ollivier, D., Kister, J. and Artaud, J. (2008) Lipid Compositions and French Registered Designations of Origins of Virgin Olive Oils Predicted by Chemometric Analysis of Mid-Infrared Spectra. Applied Spectroscopy, 62, 583-590. http://dx.doi.org/10.1366/000370208784344479
- Bombarda, I., Dupuy, N., Le Van Da, J. and Gaydou, E. (2008) Comparative Chemometric Analyses of Geographic Origins and Compositions of Lavandin var. Grosso Essential Oils by Mid Infrared Spectroscopy and Gas Chromatography. Analytica Chimica Acta, 613, 31-39. http://dx.doi.org/10.1016/j.aca.2008.02.038
- Gerlach, R., Kowalski, B. and Wold, S. (1979) Partial Least Squares Path Modeling with Latent Variables. Analytica Chimica Acta, 3, 417-421. http://dx.doi.org/10.1016/S0003-2670(01)85039-X
- Bastien, P., Esposito Vinzi, V. and Tenenhaus, M. (2005) PLS Generalised Linear Regression. Computational Statistics Data Analysis, 48, 17-46. http://dx.doi.org/10.1016/j.csda.2004.02.005
- Wangen, L. and Kowalsky, B.A. (1988) Multiblock Partial Least Squares Algorithm for Investigating Complex Chemical Systems. Journal of Chemometrics, 3, 3-20. http://dx.doi.org/10.1002/cem.1180030104
- Lis-Balchin, M. and Hart, S. (1999) Studies on the Mode of Action of the Essential Oil of Lavender (Lavandula angustifolia P. Miller). Phytotherapy Research, 13, 540-546. http://dx.doi.org/10.1002/(SICI)1099-1573(199909)13:6<540::AID-PTR523>3.0.CO;2-I
- McGimpsey, J.A. and Porter, N.G. (1999) A Growers Guide for Commercial Production. New Zealand Institute for Crop and Research Limited, Christchurch.
- Norme, N.F. (2000) Huiles essentielles—Analyse par chromatographie en phase gazeuse sur colonne capillaire— Méthode générale. AFNOR, Ed., Paris.
- Wold, S., Esbensen, K. and Geladi, P. (1987) Principal Component Analysis. Chemometrics Intelligent Laboratory System, 2, 37-52. http://dx.doi.org/10.1016/0169-7439(87)80084-9
- Fuller, M.P. and Griffiths, P.R. (1978) Diffuse Reflectance Measurements by Infrared Fourier Transform Spectrometry. Analytical Chemistry, 50, 1906-1910. http://dx.doi.org/10.1021/ac50035a045
- Martens, H. and Naes, T. (1989) Multivariate Calibration. John Wiley and Sons, Chichester.
- Liang, Y. and Kvalheim, O. (1996) Heuristic Evolving Latent Projections: Resolving Two-Way Multicomponent Data. Chemometrics and Intelligent Laboratory System, 32, 1-10.
- Dupuy, N., Duponchel, L., Amram, B., Huvenne, J.P. and Legrand, P. (1994) Quantitative Analysis of Latex in Paper Coating by ATR-FTIR Spectroscopy. Journal of Chemometrics, 8, 333-347.
- Karoui, R., Mouazen, A., Ramon, H., Schoonheydt, R. and De Baerdemaeker, J. (2006) Feasibility Study of Discriminating the Manufacturing Process and Sampling Zone in Ripened Soft Cheeses Using Attenuated Total Reflectance MIR and Fiber Optic Diffuse Reflectance VIS-NIR Spectroscopy. Food Research International, 39, 588-597. http://dx.doi.org/10.1016/j.foodres.2005.12.002
- Wold, S., Kettaneh, N. and Tjessem, K. (1996) Hierarchical Multiblock PLS and PC Models for Easier Model Interpretation and as an Alternative to Variable Selection. Journal of Chemometrics, 10, 463-482. http://dx.doi.org/10.1002/(SICI)1099-128X(199609)10:5/6<463::AID-CEM445>3.0.CO;2-L
- MacGregor, J. and Kourti, T. (1995) Process Analysis, Monitoring and Diagnosis, Using Multivariate Projection Methods. Chemometrics and Intelligent Laboratory System, 28, 3-21. http://dx.doi.org/10.1016/0169-7439(95)80036-9
- Qin, J., Vallaand, S. and Piovoso, M. (2001) On Unifying Multiblock Analysis with Application to Decentralized Process Monitoring. Journal of Chemometrics, 15, 715-742. http://dx.doi.org/10.1002/cem.667
- Jaworski, A., Wikiel, K. and Wikiel, H. (2005) Application of Multiblock and Hierarchical PCA and PLS Models for Analysis of AC Voltammetric Data. Electroanalysis, 17, 1477-1485. http://dx.doi.org/10.1002/elan.200503290
- Westerhuis, J., Kourti, T. and MacGregor, J. (1998) Analysis of Multiblock and Hierarchical PCA and PLS Models. Journal of Chemometrics, 12, 301-317. http://dx.doi.org/10.1002/(SICI)1099-128X(199809/10)12:5<301::AID-CEM515>3.0.CO;2-S
- Westerhuis, J. and Coenegracht, P. (1997) Multivariate Modelling of the Pharmaceutical Two-Step Process of Wet Granulation and Tableting with Multiblock PLS. Journal of Chemometrics, 11, 379-382. http://dx.doi.org/10.1002/(SICI)1099-128X(199709/10)11:5<379::AID-CEM482>3.0.CO;2-8
- Savitzky, A. and Golay, M. (1964) Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Analytical Chemistry, 36, 1627-1639. http://dx.doi.org/10.1021/ac60214a047
- Zhang, M., Sheng, G., Mu, Y., Li, Y., Yu, H., Harada, H. and Li, Y. (2009) Rapid and Accurate Determination of VFAs and Ethanol in the Effluent of an Anaerobic H2-Producing Bioreactor Using Near-Infrared Spectroscopy. Water Research, 43, 1823-1830. http://dx.doi.org/10.1016/j.watres.2009.01.018


