American Journal of Analytical Chemistry
Vol.4 No.3(2013), Article ID:29048,6 pages DOI:10.4236/ajac.2013.43015
Near-Infrared Spectroscopy Coupled with Kernel Partial Least Squares-Discriminant Analysis for Rapid Screening Water Containing Malathion
1Center for Instrumental Analysis, China Pharmaceutical University, Key Laboratory of Drug Quality Control and Pharmacovigilance under the Ministry of Education, Nanjing, China
2Department of Organic Chemistry, China Pharmaceutical University, Nanjing, China
3Department of Analytical Chemistry, China Pharmaceutical University, Nanjing, China
4Zhongjian Pharmaceutical Co. Ltd., Zhongshan, China
Email: *cpuxiang@yahoo.com, gcyella9122@126.com
Received January 25, 2013; revised February 28, 2013; accepted March 10, 2013
Keywords: Kernel Partial Least Squares-Discriminant Analysis; Near-Infrared Spectroscopy; Malathion; Water
ABSTRACT
Near-infrared spectroscopy coupled with kernel partial least squares-discriminant analysis was used to rapidly screen water containing malathion. In the wavenumber of 4348 cm−1 to 9091 cm−1, the overall correct classification rate of kernel partial least squares-discriminant analysis was 100% for training set, and 100% for test set, with the lowest concentration detected malathion residues in water being 1 μg∙ml−1. Kernel partial least squares-discriminant analysis was able to have a good performance in classifying data in nonlinear systems. It was inferred that Near-infrared spectroscopy coupled with the kernel partial least squares-discriminant analysis had a potential in rapid screening other pesticide residues in water.
1. Introduction
Malathion, S-(1,2-dicarbethoxyethyl)-O,O-dimethyldthiophosphate (its structural formula is shown in Figure 1) is one of the most commonly used organophosphate insecticides. It is extensively applied for controlling motile stages of mites and some other insects on fruits and vegetables. Malathion toxicity, in a manner similar to all organophosphates, is known to inhibit acetylcholinesterase and causes the accumulation of acetylcholine within synapses and the consequent overstimulation of postsynaptic receptors [1].
The reported methods to determine the malathion are high-performance liquid chromatography [2], atomic-absorption [3], carbon nanotube modified gold electrode [4], capillary electrophoresis [5], ion mobility spectrometry [6], dual fluorescence and electrochemical detection [7], CO2 laser [8]. However, these methods require expensive instrumentation or complicated pretreatment procedure, which limit their application for real-time detection of malathion. Thus, it is appropriate to seek fast, reliable and economically analytical methods of malathion by simple and relatively inexpensive instrumentation.
Near-infrared spectroscopy (NIRS) [9,10] is a spectroscopic method which contains the information of vibrations of -CH, -OH, -NH and -SH bonds. Some NIR instruments are portable, and have the potential to perform some analytical tasks out of the laboratory to gain the advantages of low cost, accuracy and test speed [11, 12]. The purpose of this study is merely to establish a rapid detection method for examining malathion residues in water.
2. Material and Experiment
2.1. Sample Preparation
Malathion (98.2% purity) was purchased from Institute for the Control of Agrochemicals, Ministry of Agriculture (ICAMA), while bottled water (Hangzhou Wahaha Group Co., Ltd., China) obtained from a local supermarket, was employed for the preparation of aqueous solutions. Stock solution of malathion (100 μg∙ml−1) was prepared in water. Among prepared samples, malathion-free samples were pure bottled water, and the malathion-containing samples were obtained by adding standard stock solution into bottled water to make the concentration from 1 to 100 μg∙ml−1.
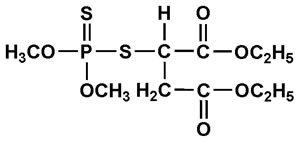
Figure 1. Structural formula of malathion.
2.2. Collection of the NIR Spectra
An YDZ1-1 NIR spectrometer (light path was shown in Figure 2) from Nanjing Instrument Co., Ltd., (Nanjing, China) was used in this study. Liquid sample was placed above an integrating sphere, and covered by a goldcoated reflector. Incident light was transmitted through the sample and then reflected back from a gold-coat reflector, which was compatible with the reflection characteristics of the instrument. After that the reflecting light passed through sample again and was transmitted to integrated sphere for detecting. So the light passed through the sample twice. Each individual spectrum was the average of 2 scans collected with a resolution of 2 nm over the wavelength range of 1100 - 2300 nm (wavenumber, 9091 - 4348 cm−1). The spectra were acquired at temperature of 25 (±1)˚C. Original NIR spectra of 100 μg·ml−1 malathion-containing water and pure water were shown in Figure 3.
2.3. Software
Chemometric analysis, including qualitative determination of malathion was performed in MATLAB 7.6.0 (Math Works Inc. Natick, USA)
3. Methods
Partial least squares (PLS) regression [13-15] is a multivariate linear projection method, which used to find the fundamental relations between the predictor matrix 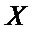 and the response matrix
and the response matrix![]() . PLS decomposes the matrix of zero-mean variables
. PLS decomposes the matrix of zero-mean variables 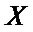 and the matrix of zero-mean variables
and the matrix of zero-mean variables ![]() into the form:
into the form:
 (1)
(1)
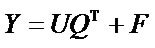 (2)
(2)
where ![]() is the
is the 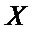 score matrix;
score matrix; 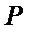 is the
is the 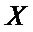 loading matrix;
loading matrix; 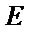 is the
is the 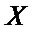 residual matrix;
residual matrix; 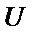 is the
is the ![]() score matrix;
score matrix; 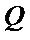 is the
is the ![]() loading matrix;
loading matrix; 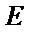 is the
is the ![]() residual matrix.
residual matrix. ![]() and
and  represent information after removing most noise. Based on the correlation between them, the linear regression model can be given by:
represent information after removing most noise. Based on the correlation between them, the linear regression model can be given by:
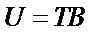 (3)
(3)
In practical, the relationship between predictor matrix and response matrix coming from experimental data is often not linear. Lambert-Beer’s law [16] only works at monochromatic radiation, system not saturated in light,

Figure 2. Light path of the YDZ1-1 NIR spectrometer.
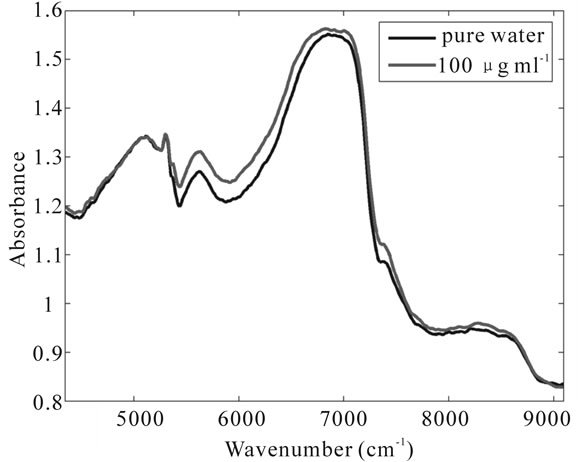
Figure 3. Original NIR spectra of 100 μg∙ml−1 malathioncontaining water and pure water.
absorbers behaving independently, absorbers being distributed homogenously and low concentrations. Apparent deviations from Lambert-Beer’s law may be caused by chemical and/or physical effects, instrumental effects or both. So non-linearity in NIR spectra may arise from factors such as highly absorbing samples, the multiplicative effect of differences in particle size among samples, nonlinear detector responses, interactions between analytes, etc. In our type of system, the spectral instruments optical scattering, detector responses and high concentration may cause non-linear behavior.
Kernel partial least squares (KPLS) is a novel kernel method developed by Rosipal et al. [17,18]. Briefly speaking, the kernel methods could be performed in two successive steps. The first step is to embed the original data via a nonlinear mapping 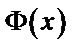 in the input space into a much higher dimensional feature space. The second step is that a linear algorithm is designed to discover the linear relationship in that feature space (see Figure 4).
in the input space into a much higher dimensional feature space. The second step is that a linear algorithm is designed to discover the linear relationship in that feature space (see Figure 4).
KPLS is a nonlinear extension of linear PLS in which the input data are transformed into a high-dimensional feature space via the nonlinear mapping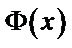 . For example, the mapping
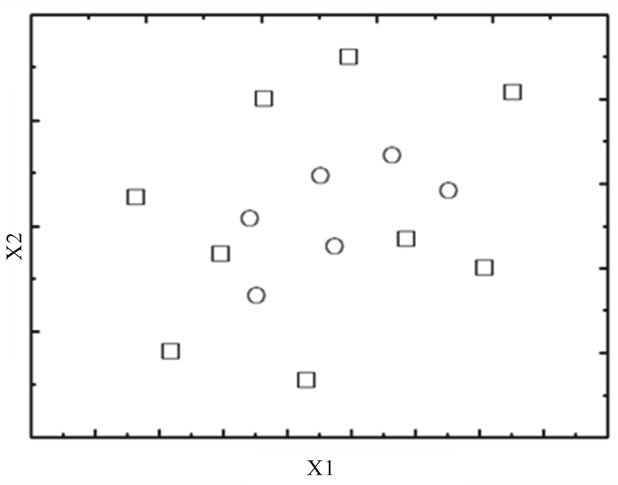
. For example, the mapping 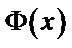 transforms the 2-D data points into a new 3-D space. Figure 5(a) shows the data
transforms the 2-D data points into a new 3-D space. Figure 5(a) shows the data

Figure 4. The mapping φ(x) embeds the data points into a feature space where the nonlinear relationship now appears linear.
 (a)
(a)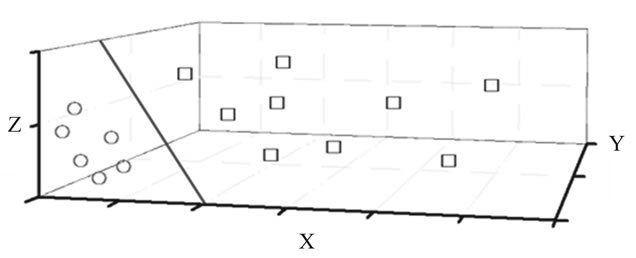 (b)
(b)
Figure 5. The linearly inseparable data points in the original input space have been linearly separable in the feature space by nonlinear mapping.
points in 2-D input space. From Figure 5(a), we can clearly see that the data points are linearly inseparable. To correctly classify the data points, a strategy adopted is to embed them into a new feature space where a linear function can be sought. Herein we continue to use the above nonlinear mapping. All data points in the new feature space are plotted in Figure 5(b). From Figure 5(b), it can be seen that the data points, which are nonlinear in the original 2-D input space, have remarkably become linearly separable in 3-D feature space. Then the PLS algorithm can then be carried out in the feature space [19- 21] . The limitation of PLS which it only can deal with linear system can be avoided.
The nonlinear transformation effect in KPLS can be completed only by dot product as described in Equation (4):
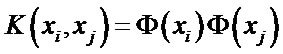 (4)
(4)
where 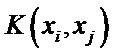 denotes kernel function, which satisfies Mercer’s theorem [17,18]. There are several kernel functions in common use. In this study we used the Radial Basis Function [22-24] :
denotes kernel function, which satisfies Mercer’s theorem [17,18]. There are several kernel functions in common use. In this study we used the Radial Basis Function [22-24] :
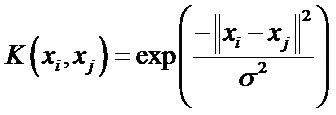 (5)
(5)
where ![]() is kernel parameter. After kernel function and kernel parameter are determined,
is kernel parameter. After kernel function and kernel parameter are determined, 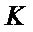 is the kernel matrix of training set, which is computed and centered by using Equations (6)-(8):
is the kernel matrix of training set, which is computed and centered by using Equations (6)-(8):
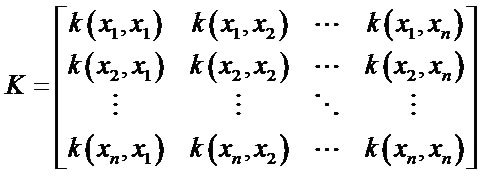 (6)
(6)
where 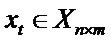 (1 ≤
(1 ≤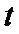 ≤ n, n: the number of training samples, m: the number of wavenumber variables) denotes training set, and
≤ n, n: the number of training samples, m: the number of wavenumber variables) denotes training set, and 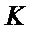 is a n-dimensional square matrix, in which each element is obtained by computing kernel function between the two training samples.
is a n-dimensional square matrix, in which each element is obtained by computing kernel function between the two training samples.
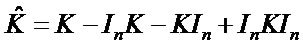 (7)
(7)
 (8)
(8)
The algorithm of KPLS can be summarized as follows:
Step 1: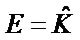 ,
, 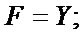
Step 2: Randomly initialize 
Step 3: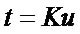 ,
, 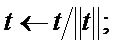
Step 4: 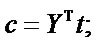
Step 5: ,
, 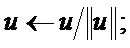
Step 6: Repeat Steps 3-6 until the convergence;
Step 7: residual matrix 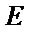 and
and 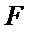 were computed,
were computed, 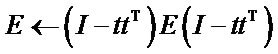 ,
,  , where
, where 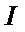 is a n-dimensional identity matrix;
is a n-dimensional identity matrix;
Step 8: turn to step 3 until the convergence of residual matrix  and
and .
.
The predicted data of training set are evaluated by using Equation (9):
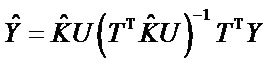 (9)
(9)
where ![]() is formed by the columns of latent vector
is formed by the columns of latent vector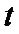 .
. 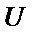 is formed by the columns of latent vector
is formed by the columns of latent vector![]() .
. ![]() is the response matrix.
is the response matrix.
For test set, 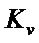 is the kernel matrix, which is computed and centered by using Equations (10)-(12).
is the kernel matrix, which is computed and centered by using Equations (10)-(12).
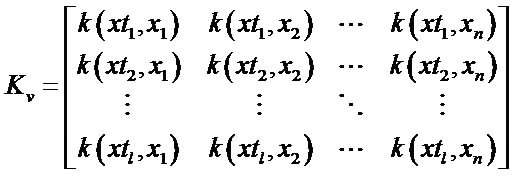 (10)
(10)
where 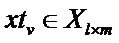 (1 ≤ v ≤ l, l: the number of test samples) denotes test set.
(1 ≤ v ≤ l, l: the number of test samples) denotes test set. 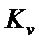 is a
is a  -dimensional matrix, in which each element is obtained by computing kernel function between test samples and training samples.
-dimensional matrix, in which each element is obtained by computing kernel function between test samples and training samples.
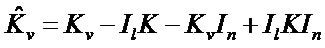 (11)
(11)
 (12)
(12)
The predicted data of test set are evaluated by using Equation (13).
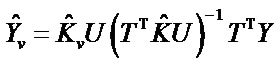 (13)
(13)
If the mode uses ![]() to be an indicator vector coding two classes: −1 for members of Class A, 1 for members of Class B, a kernel partial least squares-discriminant analysis (KPLS-DA) model is developed. The KPLS-DA model is developed by regression of the predictor matrix
to be an indicator vector coding two classes: −1 for members of Class A, 1 for members of Class B, a kernel partial least squares-discriminant analysis (KPLS-DA) model is developed. The KPLS-DA model is developed by regression of the predictor matrix 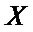 against the response matrix
against the response matrix![]() .The model based on experimental data is established in order to assign unknown samples to a previously defined sample class based on pattern of its measured features. The threshold is set to an assigned value, and a sample is considered to be categorized correctly if the predicted value lies on the same side of the threshold.
.The model based on experimental data is established in order to assign unknown samples to a previously defined sample class based on pattern of its measured features. The threshold is set to an assigned value, and a sample is considered to be categorized correctly if the predicted value lies on the same side of the threshold.
The purpose of this study is merely to establish a rapid detection method for examining malathion residues in water. It simply detects whether there are malathion residues in water, without the demand for the strict linear relationship between absorbance and concentration. So the KPLS-DA method is used to build the model in this study.
The KPLS-DA codes were written by the author according to the algorithm proposed above.
4. Results and Discussion
4.1. Selecting of Training and Test Sets
For the study, 2/3 of the spectra were utilized for training and the remaining 1/3 were kept for test. Accuracy of the models was reported by the number of misclassified samples. A total of 140 prepared samples were utilized as a training set (68 malathion-free samples and 72 malathioncontaining samples) and 70 prepared samples (34 malathion-free samples and 36 malathion-containing samples) were utilized for test.
4.2. Results of KPLS-DA Model
In this research we used the Radial Basis Function. In the indicator vector of sample classes, −1 was for water samples not containing malathion and 1 was for water samples containing malathion (1 - 100 μg∙ml−1). The threshold was set to 0 for detecting whether water containing malathion. The water containing malathion was classified correctly if the value was above 0, and for the pure water, the value was below 0. The number of factors and the value of σ2 for the final KPLS-DA model were selected by observing the correct classification rate of each class.
For the final KPLS-DA model, the number of factors was 15 and the value of σ2 was 0.045. In the wavenumber from 4348 to 9091 cm−1, the correct classification rates were 100% for training set, and 100% for test set. The predicted results of samples in training set and test set were shown in Figures 6 and 7 respectively.
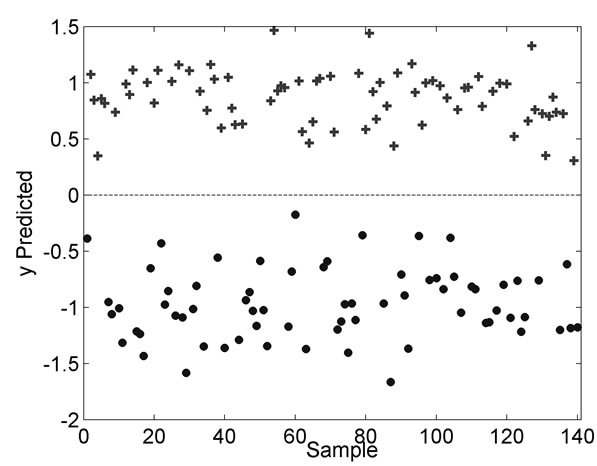
Figure 6. Predicted results of KPLS-DA in training set (“●”, pure water, “+”, malathion-containing water).

Figure 7. Predicted results of KPLS-DA in test set.
It was known that the highest concentration of malathion among misjudged samples was 1 μg∙ml−1 and satisfactory correct classification rates (100%) were obtained. So for the KPLS-DA method, the lowest concentration detected malathion residues in water was 1 μg∙ml−1.
5. Conclusion
Based on KPLS-DA method, malathion in water samples could be detected by NIR spectroscopy. Results showed that at the wavenumber from 4348 cm−1 to 9091 cm−1, a classification accuracy of 100% for training set, and 100% for test set were obtained, with the lowest concentration detected malathion residues in water being 1 μg∙ ml−1. Compared to other qualitative analysis methods, (for example, cluster analysis), KPLS-DA displayed results more directly to us in a form of scattergram and could be used as a “concentration sieve” by setting different threshod. If the threshold being the maximal concentration permitted in water, samples containing malathion at a concentration lower than the threshod were qualified, otherwise not qulified, and then rapid on-site determination could be achieved. If necessary, the nonpassing samples were left to accept the quantitative analysis of HPLC, GC, etc. Therefore, a lot of labor, material and money could be saved. The main advantages of this near infrared method are convenient sampling, no pretreatment, no consumption of organic solvent and short measurement time (5 min). It can be concluded that the proposed spectrometric methodology is a fast and environmentally friendly alternative to the classic chromatographic procedures for rapid screening water containing malathion. Although only malathion was just detected in this study, we could infer that NIR spectroscopy coupled with the KPLS-DA method may have a potential in rapid screening other pesticide residues in water.
6. Acknowledgements
This work was financially supported by the CEEUSRO combination projects of Education Ministry of Guangdong Province [No. 2007A090302100].
REFERENCES
- P. D. Moore, A. K. Patlolla and P. B. Tchounwou, “Cytogenetic Evaluation of Malathion-Induced Toxicity in Sprague-Dawley Rats,” Mutation Research/Genetic Toxicology and Environmental Mutagenesis, Vol. 725, No. 1, 2011, pp. 78-82. doi:10.1016/j.mrgentox.2011.07.007
- M. Khuhawar, A. Channar, S. Lanjwani and K. Mahar, “Indirect High Performance Liquid Chromatographic Determination of Malathion,” Journal of the Chemical Society of Pakistan, Vol. 18, No. 4, 2011, p. 306.
- M. Khuhawar, A. Chanar and I. Qazi, “Indirect Determination of Malathion Using Atomic-Absorption,” Journal of the Chemical Society of Pakistan, Vol. 16, No. 3, 2011, p. 194.
- M. Sulak and B. Keskinler, “Detection of Malathion Using a Carbon Nanotube Modified Gold Electrode,” Fresenius Environmental Bulletin, Vol. 20, No. 10, 2011.
- C. García-Ruiz, G. Alvarez-Llamas, Á. Puerta, E. Blanco, A. Sanz-Medel and M. L. Marina, “Enantiomeric Separation of Organophosphorus Pesticides by Capillary Electrophoresis: Application to the Determination of Malathion in Water Samples after Preconcentration by Off-Line Solid-Phase Extraction,” Analytica Chimica Acta, Vol. 543, No. 1, 2005, pp. 77-83. doi:10.1016/j.aca.2005.04.027
- H. Cheng, J. Li, X. Gao, J. Jia, D. Zhang and D. Zhao, “Malathion Detection Method Using Microhotplate-Based Preconcentrator and Ion Mobility Spectrometer,” International Journal of Environmental Analytical Chemistry, Vol. 92, No. 3, 2012, pp. 279-288. doi:10.1080/03067311003778623
- W. Guo, B. J. Engelman, T. L. Haywood, N. B. Blok, D. S. Beaudoin and S. O. Obare, “Dual Fluorescence and Electrochemical Detection of the Organophosphorus Pesticides-Ethion, Malathion and Fenthion,” Talanta, Vol. 15, No. 87, 2011, pp. 276-283.
- D. S. Maravić, M. S. Trtica, Š. S. Miljanić and B. B. Radak, “Detection of Malathion by the CO2 Laser: Potentials and Limitations,” Analytica Chimica Acta, Vol. 555, No. 2, 2006, pp. 259-262. doi:10.1016/j.aca.2005.09.006
- Y. Roggo, P. Chalus, L. Maurer, C. Lema-Martinez, A. Edmond and N. Jent, “A Review of Near Infrared Spectroscopy and Chemometrics in Pharmaceutical Technologies,” Journal of Pharmaceutical and Biomedical Analysis, Vol. 44, No. 3, 2007, pp. 683-700. doi:10.1016/j.jpba.2007.03.023
- K. Wang, G. Chi, R. Lau and T. Chen, “Multivariate Training of Near Infrared Spectroscopy in the Presence of Light Scattering Effect: A Comparative Study,” Analytical letters, Vol. 44, No. 5, 2011, pp. 824-836. doi:10.1080/00032711003789967
- H. Huang, H. Yu, H. Xu and Y. Ying, “Near Infrared Spectroscopy for On/In-Line Monitoring of Quality in Foods and Beverages: A Review,” Journal of Food Engineering, Vol. 87, No. 3, 2008, pp. 303-313. doi:10.1016/j.jfoodeng.2007.12.022
- T. Woodcock, C. O’Donnell and G. Downey, “Review: Better Quality Food and Beverages: The Role of Near Infrared Spectroscopy,” Journal of Near Infrared Spectroscopy, Vol. 16, No. 1, 2008, pp. 1-29. doi:10.1255/jnirs.758
- J. H. Kalivas, “Multivariate Training: An Overview,” Analytical Letters, Vol. 38, No. 14, 2005, pp. 2259-2279. doi:10.1080/00032710500315904
- W. F. C. Rocha, B. G. Vaz, G. F. Sarmanho, L. H. C. Leal, R. Nogueira, V. F. Silva and C. N. Borges, “Chemometric Techniques Applied for Classification and Quantification of Binary Biodiesel/Diesel Blends,” Analytical Letters, Vol. 45, No. 16, 2012, pp. 2398-2411. doi:10.1080/00032719.2012.686135
- S. Wold, M. Sjöström and L. Eriksson, “PLS-Regression: A Basic Tool of Chemometrics,” Chemometrics and Intelligent Laboratory Systems, Vol. 58, No. 2, 2001, pp. 109-130. doi:10.1016/S0169-7439(01)00155-1
- K. Buijs and M. Maurice, “Some Considerations on Apparent Deviations from Lambert-Beer’s Law,” Analytica Chimica Acta, Vol. 47, No. 3, 1969, pp. 469-474. doi:10.1016/S0003-2670(01)95647-8
- R. Rosipal, “Kernel Partial Least Squares for Nonlinear Regression and Discrimination,” Neural Network World, Vol. 13, No. 3, 2003, pp. 291-300.
- R. Rosipal and L. J. Trejo, “Kernel Partial Least Squares Regression in Reproducing Kernel Hilbert Space,” The Journal of Machine Learning Research, Vol. 2, 2002, pp. 97-123.
- K. Kim, J. M. Lee and I. B. Lee, “A Novel Multivariate Regression Approach Based on Kernel Partial Least Squares with Orthogonal Signal Correction,” Chemometrics and Intelligent Laboratory Systems, Vol. 79, No. 1, 2005, pp. 22-30. doi:10.1016/j.chemolab.2005.03.003
- B. M. Nicolai, K. I. Theron and J. Lammertyn, “Kernel PLS Regression on Wavelet Transformed NIR Spectra for Prediction of Sugar Content of Apple,” Chemometrics and Intelligent Laboratory Systems, Vol. 85, No. 2, 2007, pp. 243-252. doi:10.1016/j.chemolab.2006.07.001
- J. I. Park, L. Liu, X. P. Ye, M. K. Jeong and Y. S. Jeong, “Improved Prediction of Biomass Composition for Switchgrass Using Reproducing Kernel Methods with Wavelet Compressed FT-NIR Spectra,” Expert Systems with Applications, Vol. 39, No. 1, 2012, pp. 1555-1564. doi:10.1016/j.eswa.2011.05.012
- Q. B. Li, L. N. Li and G. J. Zhang, “A Nonlinear Model for Training of Blood Glucose Noninvasive Measurement Using Near Infrared Spectroscopy,” Infrared Physics & Technology, Vol. 53, No. 5, 2010, pp. 410-417. doi:10.1016/j.infrared.2010.07.012
- B. Walczak and D. Massart, “The Radial Basis Functions —Partial Least Squares Approach as a Flexible Non-Linear Regression Technique,” Analytica Chimica Acta, Vol. 331, No. 3, 1996, pp. 177-185. doi:10.1016/0003-2670(96)00202-4
- B. Walczak and D. Massart, “Application of Radial Basis Functions—Partial Least Squares to Non-Linear Pattern Recognition Problems: Diagnosis of Process Faults,” Analytica Chimica Acta, Vol. 331, No. 3, 1996, pp. 187-193. doi:10.1016/0003-2670(96)00206-1
NOTES
*Corresponding author.

