ABSTRACT

Fins are the extended surfaces through which heat transfer takes place to keep the surface cool. Fins of various configurations are presently used ranging from automobile engine cooling to cooling of computer parts. Note that in a fin majority of the heat transfer to atmosphere is by convection and therefore in the present research, and importance is given to variation of temperature along the length of the fin which in turn gives rate of heat transfer. In the present research a solid rectangular aluminum fin and the same rectangular fin with different perforations (2, 4, 8 and 10) were compared analytically, experimentally and its validity through finite element analysis for its temperature distribution along the length. From the present research it is observed that the mathematical and FEA for a solid rectangular fin without perforations are converging within ±1˚C and rectangular fin with 10 perforations are converging within ±2˚C and hence the validity.

Keywords:

Fin, Mathematical, Temperature, FEA and Perforations

1. Introduction

The basic law that governs the convective heat transfer is Newton’s law of cooling given by:

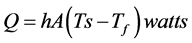(1)

where: Ts: the surface temperature ˚C, T_f: the fluid temperature ˚C, h: the convective heat transfer coefficient w/m² ˚C, A: surface area, m²

Note that in the above equation, film coefficient of heat transfer or the convective heat transfer coefficient “h” is very important which mainly depends on the type of the surface, size, shape, its temperature, surface finish etc. Most of the research, mathematical analysis and dimensional analysis are confined in finding “h”. In addition to the above, for fins the temperature distribution along its length also become important.

The expulsion of overabundance warmth from framework parts is fundamental to abstain from harming impacts of overheating. Thusly the improvement of warmth exchange is a vital subject of warm designing [1] . Heat exchange rate might be expanded by expanding the warmth exchange coefficient between a surface and its encompassing, or by expanding the warmth exchange zone of the surface. Much of the time, the zone of warmth exchange is expanded by developing surfaces. These amplified surfaces are called fins.

Balances are utilized to improve convective warmth move in an extensive variety of designing applications and offer a handy method for accomplishing a substantial aggregate warmth exchange surface range without the utilization of an over the top measure of essential surface zone [2] . Fins are generally connected for warmth administration in electrical apparatuses, for example, PC power supplies or substation transformers. Different applications incorporate motor cooling, Condensers in refrigeration and aerating and cooling [3] . Fins as warmth exchange improvement gadgets have been very regular. The diverse materials like mild steel, stainless steel, aluminum, and silver, copper and so on are utilized for making fins. As the stretched out surface innovation keeps on developing, new outline thoughts have been risen including fins made of anisotropic composites, permeable media, hindered and punctured plates. Because of popularity for light weight, smaller and sparing fins, the enhancement of balance size is of awesome significance [4] .

Along these lines, fins must be intended to accomplish most extreme warmth expulsion with least material use considering the simplicity of the balance fabricating. The change in warmth exchange coefficient is ascribed to the restarting of the warm limit layer after every an interference [5] . Accordingly punctured plates and fins speak to a case of surface intrusion. Current study intends to foresee the temperature drop more than a few round apertures of expansion in number. Different parameters like warm flux and warm inclination are analyzed over various numbers of round holes [6] . In this investigation ANSYS FEA software is utilized for lattice and unraveling.

In the examination of warmth trade, cutting edges are surfaces that stretch out from a thing to manufacture the rate of warmth trade to or from nature by growing convection. The measure of conduction, convection, or radiation of an article chooses the measure of warmth it trades [7] . Extending the temperature incline between the article and the earth, growing the convection heat trade coefficient, or extending the surface zone of the thing constructs the glow trade. Occasionally it is not achievable or down to earth to change the underlying two choices. In this way, adding a cutting edge to a thing assembles the surface zone and can rarely be a calm response for warmth trade issues [8] .

Finally, it is well known that major heat transfer from the fin is by convection and performance of a fin is evaluated by its efficiency and effectiveness.

2. Literature Review

Types of Fins in Use

a. Straight Fins (Figure 1)

b. Annular (circumferential) fins (Figure 2)

c. Spine or pin fins (Figure 3)

There are various examination related to warmth trade and weight drop of channels with pin cutting edges, which are limited to stick parities with round or couple of different cross territories. The genuine warmth trade takes by two modes i.e. by conduction took after by convection. Heat trade through the solid

to the surface of the solid happens through conduction whereas from the surface to the surroundings happens by convection. Further warmth trade may be by normal convection or by obliged convection.

Bayram Sahin and Alparslan Demir [9] from their research concluded that, the use of the square stick cutting edges may incite warmth trade change. Both lower elbowroom extent and lower between parity scattering extent and likewise cut down Reynolds numbers are proposed for higher warm execution. R. Karthikeyan and R. Rathnasamy [10] concluded from their research that, for a given Reynolds number, the pin-edge show with smaller buries fin separation gives higher execution than those with higher cover equalization partitions. Another researcher found that, most in-line square stick equalization bunches have poorer warmth move than an in-line round pin fin cluster show wonderful warmth trade at high Reynolds number. The perfect between equalization pitches are directed by the greatest Nusselt number at a given pumping power [11] . Connections giving the typical Nusselt number for each outline as a part of the Reynolds number were created few researchers [12] . Amol B., Dhumne, Hemant S. and Farkade [13] focused on the trial examination of on warmth exchange upgrade and the relating weight drop over a level surface equipped with barrel molded cross sectional punctured pin equalizations in a rectangular channel. Their research showed that the usage of the barrel formed punctured pin fins prompts heat trade update than the solid round and empty equalizations. Both lower breathing space extent and lower between parity scattering extent and nearly cut down Reynolds numbers are proposed for higher warm execution. In one more investigation the researchers found that, glow trade by short stick edges instaggered plans. According to their results, longer stick equalizations (H/d = 4) trade more warmth than shorter pin-parities (H/d = 1/2 and 2) and the exhibit found the center estimation of warmth trade with eight segments of pin-adjusts to some degree surpasses that with only four lines [14] . Vanfossen G. J. and Brigham B. A. [15] focused their research on the ordinary warmth trade coefficient on the pin surface is around 35% greater than that on the end dividers.

Metzger et al. [16] investigated the effects of pin-edge shape and show presentation on the glow trade and the weight incident in pin-equalization bunches. They demonstrated by their results that the use of round and empty pin-parities with a group introduction amongst astonished and in-line can now and again propel the glow trade, while fundamentally decreasing weight. Others have also reported from their investigation that, another way to deal with upgrade heat swapping scale is touse spaces which allow the stream to encounter the pieces [17] . Yatendra Singh, Tomar, Sahu M. M [18] mulled over that the warm resistance and weight drop are considered as the distinctive warm execution properties. Their studies have exhibited that the convection heat conversion standard from equalization bunches depends on upon all geometric parameter, parity material and base-to-encompassing temperature contrast. The elliptic pin equalization exhibits the most insignificant weight drops. For the same surface zone at a settled pumping power, the elliptic pin edge has the smallest warm resistance for the stunned course of action [19] .

3. Relevance of the Research

Fins are the extended surfaces through which heat transfer takes place. In the present investigation the surface area is increased by providing perforations in the fins. This in turn increases effectiveness and efficiency of the fin. So far no attempt has been made to provide perforations in the solid aluminum fin to increase the surface area and hence the present research was under taken to fill the void.

4. Experimental Procedure

Figure 4 shows the experimental set up showing temperature recorder, thermocouples etc. along with the heat source at the center attached with fins having perforations with a maximum of 10 holes. The power supplied was 40 watts to heat the base of the fin.

4.1. Mathematical Analysis for a Solid Fin Temperature Distribution

Figure 5 shows a rectangular aluminum fin indicating the details regarding area, perimeter, temperature etc.

The most popular energy balance equation used to find the heat transfer through fins mathematically (for steady state condition) is given by:

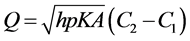(2)

where Q: rate of hear transfer, watts, h: convective heat transfer coefficient w/m²

˚C, P: the perimeter of the fin, m, K: thermal conductivity, w/m ˚C, A: area, m² and C₁, C₂ are constants obtained by applying the limits.

Above equation is modified to find temperature distribution based on the tip condition.

Equation (3) below is used to find analytically the fin temperature over a distance with given boundary conditions [20] .

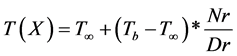(3)

where,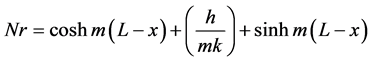

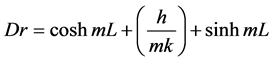
where Nr = numerator term and Dr = denominator term

4.2. Heat Transfer Coefficient Using Vertical Plate Correlation

Correlations given below are used to find the heat transfer coefficient using dimensional analysis for vertical plate [21] .

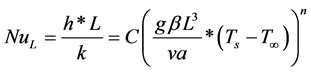(4)

where,

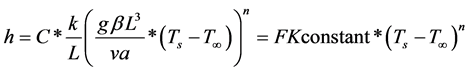
(where constants c = 0.59, n = 0.25)

4.3. Mathematical and Finite Element Modeling of Rectangular Fin with Number of Perforations (2, 4, 8 and 10)

For analysis and comparison purpose, rectangular aluminum fin with 2, 4, 8 and 10 perforations was considered but for discussion only fin with 10 perforations is presented in this present paper.

Mathematically, the heat transfer coefficient is calculated using the vertical plate correlation discussed in Section 4.2. using the following details.

Actual open area = 10 * (pi/4 * 12²) = 1130.9 mm²

Maximum possible perforation open area = 15 * (pi/4 * 12²) = 1696.45 mm²

Due to perforations, boundary layer detachment and re-attachment phenomenon occurs. This is accommodated by a multiplying factor in the formula given below where h_ps is the convective heat transfer coefficient.

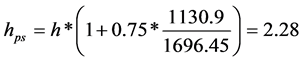(5)

4.4. Finite Element Analysis (FEA)

Element types used for the analysis are: SOLID70 element and SURF152 element. The steps involved in the present FEA are a) 3D rectangular fin modelling and meshing b) Creation of surf elements for the modeling c) Applying the boundary conditions and source temperature d) Applying the material property (aluminum) e) Obtaining the steady state thermal contours.

Finally the mathematical, experimental and ANSYS FE analysis are compared for the validity. Initially this method was used for solid rectangular fin under steady state condition and later to rectangular fin with perforations.

Note that for a solid fin, only mathematical and FE analysis was performed whereas for a rectangular fin with perforations, mathematical analysis and experimental (temperature measurement) results are compared as a check and finally the validity by FEA.

5. Results and Discussions

5.1. Rectangular Fin without Perforations (Solid Fin)

Figure 6 shows FE modeling and analysis for a rectangular fin indicating the thermal contour. Temperature calculation along the length of the fin using Equation (3) is tabulated in Table 1. Figure 7 shows superpose of FE analysis and analytical calculation as indicated in Table 1.

It is observed from Table 1 that the root temperature 200˚C goes on decreases as fin length increases and reaches 192.4˚C at the tip. From Figure 6 it is again observed that the FE modeling follows the same pattern that the temperature monotonically decreases from 200˚C to 192˚C. Hence, it is concluded from the present research that keeping the base (root) temperature at 200˚C with power supply of 40 watts, a solid rectangular fin reaches a temperature of 192.4˚C at the tip. Figure 7 shows that the mathematical and FEA that for a solid rectangular fin without perforations are converging within ±1˚C and hence the validity of FEA by mathematical analysis.

5.2. Rectangular Fin with Perforations

Figure 8 below shows the experimental results of temperature measurement

along the length of the fin with a power supply of 40 watts for a rectangular fin with different perforations. Temperature was measured using thermocouples along the length of the fin.

Figure 9 below shows the temperature calculated using mathematical analysis for a rectangular fin containing 2, 4, 8 and 10 perforations.

Figures 10-12 below shows the FE models of thermal contour (steady state), thermal gradient and thermal heat flux for a rectangular fin containing 10 perforations.

Figure 10. Thermal contour (FE analysis).

Figure 13 below shows the comparison of mathematical analysis with FEA for a rectangular fin with 10 perforations.

It is observed from Figure 8 and Figure 9 that both experimental and mathematical analysis follows almost the same pattern of temperature distribution along the length of the perforated fin. It is also observed from Figure 8 and Figure 9 that the temperature of fin at the trailing surface is decreasing with increase the number of perforations in the fin. This indicates that heat transfer

increases with perforations having full connectivity between the base and the fin. It is observed from the present research that keeping the base (root) temperature at 200˚C with power supply of 40 watts, rectangular fin with 10 perforations reaches 184.2˚C at the tip. This shows that rectangular fin with perforations removes more heat compared to a solid fin.

From Figure 10 it is observed that FE analysis follows the same pattern as that of mathematical and experimental values i.e., the root temperature 200˚C continuously decreases to 184˚C at the tip.

From Figure 13 where analytic and FEA are superposed, it is seen that the mathematical and FEA of rectangular fin with 10 perforations are converging within ±2˚C and hence the validity of FEA with mathematical and experimental analysis.

6. Conclusions

Extended surfaces i.e., fins are used to remove heat from the component to keep it cool. It is observed from the present research that keeping the base (root) temperature at 200˚C with power supply of 40 watts, a solid rectangular fin reaches a temperature of 192˚C at the tip whereas the same fin with 10 perforations reaches 184˚C at the tip. This shows that rectangular fin with perforations removes more heat compared to that of a solid fin. It is also observed from the research that this temperature fall gradually from fin with 2, 4, 8 and 10 perforations thus the heat removal gradually decreases with increase in perforations. Heat flux also follows the same pattern along the length of the fin as that of the temperature.

In the present research it is observed from the mathematical and FEA that for a solid rectangular fin without perforations are converging within ±1˚C and rectangular fin with 10 perforations are converging within ±2˚C and hence the validity.

Cite this paper

Hemanth, J. (2017) Experimental, Mathematical and Finite Element Analysis (FEA) of Temperature Distribution through a Rectangular Fin with Circular Perforations. Modeling and Numerical Simulation of Material Science, 7, 19-32. https://doi.org/10.4236/mnsms.2017.72002

References