Modeling and Numerical Simulation of Material Science
Vol.05 No.02(2015), Article ID:55740,8 pages
10.4236/mnsms.2015.52004
New Orbital-Free Approach for Density Functional Modeling of Large Molecules and Nanoparticles
V. Zavodinsky1, O. Gorkusha2
1Institute of Materials Science, Russian Academy of Sciences, Khabarovsk, Russia
2Institute of Applied Mathematics, Russian Academy of Sciences, Khabarovsk, Russia
Email: vzavod@mail.ru, o_garok@rambler.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 March 2015; accepted 12 April 2015; published 16 April 2015
ABSTRACT
Development of the orbital-free (OF) approach of the density functional theory (DFT) may result in a power instrument for modeling of complicated nanosystems with a huge number of atoms. A key problem on this way is calculation of the kinetic energy. We demonstrate how it is possible to create the OF kinetic energy functionals using results of Kohn-Sham calculations for single atoms. Calculations provided with these functionals for dimers of sp-elements of the C, Si, and Ge periodic table rows show a good accordance with the Kohn-Sham DFT results.
Keywords:
Orbital Free, Kinetic Functional, Modeling, Nanosystems

1. Introduction
The modern materials science and macromolecular chemistry combining nano, micro, and macro scales represent special inquiries to modeling of atomic interactions. When the system contains millions or billions of electrons, the task to find its quantum-mechanical state using wave functions (orbitals) becomes almost insoluble. Intensive attempts to develop an orbital-free (OF) approach for modeling of polyatomic systems based on the density functional theory (DFT) [1] were made by a number of groups in last two decades [2] -[10] . Most of them were developed within a pseudopotential approach, however, recently even an all-electron version of the OF method appeared [11] . Unfortunately, still now there is not a good comparison between OF and the KS results. Perhaps, the reason of this unluckiness is that all OF works stand on idea of using some universal functionals for kinetic energy―in approaches of Tomas-Fermi [12] [13] , Weizsacker [14] , and their modifications and combinations [10] [11] . However, in recent years a number of works appeared [15] [16] in which it was shown that the hypothesis of existence of universal density functional was incorrect, and that first of all it concerned the functional of kinetic energy (FKE). Nevertheless, the problem of development of the efficient approach for the OF-modeling of polyatomic systems remains tempting and actual. In our recent papers [17] [18] , we have showed how it is possible, using single-atoms calculations by the Kohn-Sham DFT method (KS-DFT) [19] , to find numerically the kinetic energy functionals for atoms, and then to use them for orbital-free modeling of atomic interactions. We calculated equilibrium distances, and binding energies for dimers contained Al, Si, and P atoms. Now we present an expansion of our method for other sp-species.
2. Methodology
First, confirm that you have the correct template for your paper size. This template has been tailored for output on the custom paper size (21 cm × 28.5 cm).
As it is known the DFT claims that the energy Eel of the ground state of any quantum system can be found by minimization of the some functional depending only on the electronic density of this system ρ:
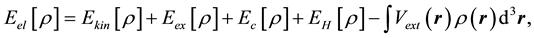 (1)
(1)
where Vext is an external potential, Ekin is kinetic energy, Eex is exchange energy, Ec is correlation energy, and EH is Hartree energy: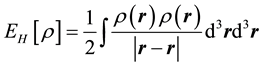 .
.
The total energy Etot is given by integral:
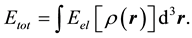 (2)
(2)
Minimization of (1) with a condition 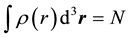 means solving the following equation:
means solving the following equation:
 (3)
(3)
where μ is the Lagrange parameter having a sense of the electron chemical potential.
Introducing , we obtain the equation
, we obtain the equation
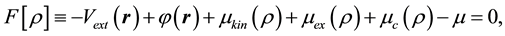 (4)
(4)
where ,
, 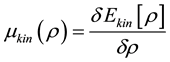 ,
, 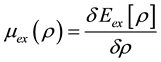 ,
,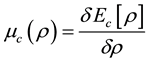 .
.
There are some realistic approximations for exchange  and correlation
and correlation 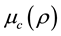 potentials; the potential of electron-electron repulsion
potentials; the potential of electron-electron repulsion  may be calculated using Fourier transformations; the external potential
may be calculated using Fourier transformations; the external potential  usually consists of atomic potentials or of pseudopotentials. The key problem is to find the potential of kinetic energy
usually consists of atomic potentials or of pseudopotentials. The key problem is to find the potential of kinetic energy . In the Kohn-Sham approach this problem is absent because the kinetic energy is calculated using electron orbitals (wave functions).
. In the Kohn-Sham approach this problem is absent because the kinetic energy is calculated using electron orbitals (wave functions).
Quantum mechanical pseudopotentials are usually constructed for different angular states. Thus, we have to present the total density as a sum of partial densities:

For the s-p case, we may write the equations

where 






3. Results and Discussion
3.1. Single Atoms
If we calculate the ground state of an atom in the KS-DFT pseudopotential approach, we may declare that its partial electron densities minimize their energy functionals or in other words, Equation (6) are satisfied. Thus, we can find 


In order to calculate the kinetic energy we have to make integration firstly on ρ and then on r:

Therefore, we have to pass from the coordinate determination of 

Therefore, we can write the partial kinetic functionals 


Let us consider Si, Al, and P atoms as typical atoms with s, p electrons. For constructing of pseudo potentials and calculation of equilibrium densities and energies we will use the FHI98pp [20] and FHI96md [21] packages widely used for KS-DFT calculations. Exchange and correlation potentials we will consider in the local density approximation [22] [23] . Then the partial densities ρs(r) and ρp(r) will look for SI as follows (Figure 1).
As it was said above we can use dependencies ρs(r) and ρp(r) for passing from the coordinate determination 



see that universal dependence doesn’t exist. There are essential differences between s and p components; and the curves received for various atoms, considerably differ from each other. However, we see also important common features of these curves.
Figure 1. Partial densities ρs(r) and ρp(r) for a single Si atom. The point of minima corresponds to the atomic center. The solid line shows s-states; the points demonstrate p-states.
Figure 2. Partial kinetic energy potentials 

Figure 3. Dependencies 

All of them have regions with reverse motion (i.e. two-branches), and besides, each curve has the limited range of definition corresponding to the maximum value of density for this atom. Reverse motions of curves correspond to densities situated inside pseudopotential spheres. To avoid ambiguity, we will separately determine densities inside spheres and outside and will speak about separate kinetic functionals



3.2. Atomic Dimers
An attempt to consider atomic interactions in dimers leads immediately to the problem: atomic densities are summarized and under certain conditions (a close arrangement of atoms) the total electronic density can signifi-
cantly exceed the maximum value, for which the single-atom function 




sities? Probably, the exact answer to these questions will be found in some future, but now we offer other, an approximate way for finding of equilibrium density and energy of interacting atoms. It seems to us that one of the possible practical ways is to construct analytical formulas, which can extrapolate data calculated for single atoms. In the best case, such formulas may be the same for some different kinds of atoms, but in the general case, each specie needs its own expressions for kinetic energy functionals. Calculations of equilibrium interatomic distances and binding energies for atomic dimers may be used for testing of constructed formulas.
We have tested the following expressions for some s-p dimers:

Calculations were performed using a cubic cell of 30 Bohr size (1 Bohr = 0.0529 nm) divided by the 100 × 100 × 100 grid for integration. To find the binding energies Eb and equilibrium distances d0 between atoms in dimers we consider the total energy Etot as a sum of the electron energy Eel and the energy of “ion-ion” repulsion

where Z1 and Z2 are positive charges of ions with numbers 1 and 2 situated at R1 and R2 points. The binding energy per atom Eb was determined as follows:

where Etot is the energy of two interacted atoms, E1 and E2 are energies of free atoms.
Results of calculations were compared with results obtained in the framework of the KS-DFT approach using the FHI96md package. The preference was given to this package because the FHI96md package applies the same pseudopotentials and exchange-correlation approximations as we used.
Figure 4 demonstrates the dependence of the binding energy (per atom) for Si2 on the distance between atoms; and Figure 5 shows changes of the total electron density during the iteration process for various interatomic distances. We can see that our results correlate with results obtained by the KS-DFT method: the both methods lead to similar changes of density in the process of calculation.
Results (equilibrium distances d0 and binding energies Eb) for atomic dimers of the Na-Cl and K-Br rows are collected in Table 1 and Table 2, correspondingly, in comparison with results obtained by us using the FHI96md package. One can seen that our OF results for the most of dimers are close to the KS-DFT ones. Exceptions are dimers of bivalent elements (Mg, Ca) and dimers of six-seven-valence atoms (S, Cl and Se, Br); the nature of this peculiarity will be studied later in a special work.
In must be noted that we have met some troubles in attempts to expanse our approach to dimers of small atoms (B, C, N, and O). Namely, to obtain good results for equilibrium distances and binding energies (shown
in Table 3) we used for them different expressions for



For B:
For C:
For N:
For O:
Thus, we can conclude that using of special expressions for the kinetic energy functional (unique for each kind of atoms) allows us to describe interactions of atoms with compact densities. Note that these elements (B, C, N, and O) are very important components of many useful materials, molecules and compounds.
Figure 4. Binding energy (per atom) in the Si2 dimer versus the interatomic distance. Solid circles represent our OF results; hole circles illustrate calculations by the Kohn-Sham method (the FHI96md package).
Figure 5. Changes of the total electron density in the Si2 dimer during the iteration process for various interatomic distances. The upper row (A, B, and C) demonstrates calculations by our method; the low row (D, E, and F) shows results of the FHI96md Kohn-Sham calculations. The B and E panels correspond to equilibrium distances. Dashed curves describe initial densities; solid ones illustrate final functions.
Table 1. Equilibrium distances d0 (Å) and binding energies Eb (eV, per atom) for dimers of the Na-Cl row.
Table 2. Equilibrium distances d0 (Å) and binding energies Eb (eV, per atom) for dimers of the K-Br row.
Table 3. Equilibrium distances d0 (Å) and binding energies Eb (eV, per atom) for dimers of B, C, N, and O.
4. Conclusion
We have demonstrated a principal possibility to find equilibrium densities, interatomic distances, and binding energies in the orbital-free approach using simple functionals of kinetic energy. However, in general case, FKE cannot be described by any universal formula and must be constructed for the each species. This work does not represent the finished algorithms for modeling of polyatomic systems; we have showed only a basic possibility to create such code. Still, it is necessary to include in the GGA options, spin polarization, and certainly to expand it to d-atoms. Besides, as it is our main future task, it is necessary to add calculations of forces operating on atoms in order to pass from dimers to more complicated objects.
Acknowledgements
This work was supported financially by the Far East Branch of the Russian Academy of Sciences; the grant #15-I-4-004 o.
References
- Hohenberg, H. and Kohn, W. (1964) Inhomogeneous Electron Gas. Physical Review, 136, B864-B871. http://dx.doi.org/10.1103/PhysRev.136.B864
- Wang, Y.A. and Carter, E.A. (2000) Orbital-Free Kinetic-Energy Density Functional Theory. In: Schwartz, S.D., Ed., Progress in Theoretical Chemistry and Physics, Kluwer, Dordrecht.
- Chen, H.J. and Zhou, A.H. (2008) Orbital-Free Density Functional Theory for Molecular Structure Calculations. Numerical Mathematics: Theory, Methods and Applications, 1, 1-28.
- Zhou, B.J., Ligneres, V.L. and Carter, E.A. (2005) Improving the Orbital-Free Density Functional Theory Description of Covalent Materials. Journal of Chemical Physics, 122, Article ID: 044103. http://dx.doi.org/10.1063/1.1834563
- Hung, L. and Carter, E.A. (2009) Accurate Simulations of Metals at the Mesoscale: Explicit Treatment of 1 Million Atoms with Quantum Mechanics. Chemical Physics Letters, 475, 163-170. http://dx.doi.org/10.1016/j.cplett.2009.04.059
- Karasiev, V.V. and Trickey, S.B. (2012) Issues and Challenges in Orbital-Free Density Functional Calculations. Computational Physics Communications, 183, 2519-2527. http://dx.doi.org/10.1016/j.cpc.2012.06.016
- Karasiev, V.V., Chakraborty, D., Shukruto, O.A. and Trickey S.B. (2013) Nonempirical Generalized Gradient Approximation Free-Energy Functional for Orbital-Free Simulations. Physical Review B, 88, 161108-161113(R). http://dx.doi.org/10.1103/PhysRevB.88.161108
- Wesolowski, T.A. (2005) Approximating the Kinetic Energy Functional Ts[ρ]: Lessons from Four-Electron Systems. Molecular Physics, 103, 1165-1167. http://dx.doi.org/10.1080/00268970512331339341
- Watson, S.C. and Carter, E.A. (2000) Linear-Scaling Parallel Algorithms for the First Principles Treatment of Metals. Computational Physics Communications, 128, 67-92. http://dx.doi.org/10.1016/S0010-4655(00)00064-3
- Ho, G.S., Ligneres, V.L. and Carter, E.A. (2008) Introducing PROFESS: A New Program for Orbital-Free Density Functional Theory Calculations. Computational Physics Communications, 179, 839-854. http://dx.doi.org/10.1016/j.cpc.2008.07.002
- Lehtomäki, J., Makkonen, I., Caro, M.A., Harju, A. and Lopez-Acevedo, O. (2014) Orbital-Free Density Functional Theory Implementation with the Projector Augmented Wave Method. Journal Chemical Physics, 141, 234102.
- Τhоmas, L.Η. (1926) The Calculation of Atomic Field. Proceedings of the Cambridge Philosophical Society, 23, 542- 548.
- Fermi, E. (1927) Un metodo statistico per la determinazione di alcune prioprietà dell’atomo. Rendiconti Academia Dei Lincei, 6, 602-607.
- Von Weizsacker, C.F. (1935) Zur Theorie de Kernmassen. Zeitschrift für Physik, 96, 431-458. http://dx.doi.org/10.1007/BF01337700
- Sarry, A.M. and Sarry, M.F. (2012) To the Density Functional Theory. Physics of Solid State, 54, 1315-1322. http://dx.doi.org/10.1134/S1063783412060297
- Bobrov, V.B. and Trigger, S.A. (2013) The Problem of the Universal Density Functional and the Density Matrix Functional Theory. Journal of Experimental and Theoretical Physics, 116, 635-640. http://dx.doi.org/10.1134/S1063776113040018
- Zavodinsky, V.G. and Gorkusha, O.A. (2012) A Simple Quantum Mechanics Way to Simulate Nanoparticles and Nanosystems without Calculation of Wave Functions. ISRN Nanomaterials, 2012, Article ID: 531965.
- Zavodinsky, V.G. and Gorkusha, O.A. (2014) A Practical Way to Develop the Orbital-Free Density Functional Calculations. Physics Science International Journal, 4, 880-891. http://dx.doi.org/10.9734/PSIJ/2014/10415
- Kohn, W. and Sham, J.L. (1965) Self-Consistent Equations including Exchange and Correlation Effects. Physical Review, 140, A1133-A1138. http://dx.doi.org/10.1103/PhysRev.140.A1133
- Fuchs, M. and Scheffler, M. (1999) Ab Initio Pseoudopotentials for Electronic Structure Calculations of Poly-Atomic Systems Using Density-Functional Theory. Computational Physics Communications, 119, 67-98. http://dx.doi.org/10.1016/S0010-4655(98)00201-X
- Beckstedte, M., Kley, A., Neugebauer, J. and Scheffler, M. (1997) Density-Functional Theory Calculations for Poly- Atomic Systems: Electronic Structure, Static and Elastic Properties and ab Initio Molecular Dynamics. Computational Physics Communications, 107, 187-205. http://dx.doi.org/10.1016/S0010-4655(97)00117-3
- Perdew, J.P. and Zunger, A. (1981) Self-Interaction Correction to Density Functional Approximation for Many-Elec- tron Systems. Physical Review B, 23, 5048-5079. http://dx.doi.org/10.1103/PhysRevB.23.5048
- Ceperley, D.M. and Alder, B.J. (1980) Ground State of the Electron Gas by a Stochastic Method. Physical Review Letters, 45, 566-569. http://dx.doi.org/10.1103/PhysRevLett.45.566











