Modeling and Numerical Simulation of Material Science
Vol.05 No.01(2015), Article ID:52924,13 pages
10.4236/mnsms.2015.51001
Prediction of the Microstructural Variations of Cold-Worked Pure Aluminum during Annealing Process
Hamid Reza Rezaei Ashtiani*, Peyman Karami
School of Mechanical Engineering, Arak University of Technology, Arak, Iran
Email: *hr_rezaei@iust.ac.ir, *hr_rezaei@arakut.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 September 2014; revised 15 October 2014; accepted 26 October 2014
ABSTRACT
The mechanical properties such as hardness and ultimate tensile strength of metals depend on the grain size, which have to be properly controlled and optimized to ensure the better economy and desirable mechanical characteristics of the metals. In order to study the microstructure evolution of AA1070, many experimental tests were conducted at different cold working and annealing conditions. Utilizing the experimental results, the static recrystallization and grain growth behavior of AA1070 have been investigated and the developed equations that can be used to the FEM of the annealing process have been obtained. The agreement between numerical modeling and experimental results is reasonably good for this material. The results showed that the recrystallization and grain growth behavior of AA1070 was evidently affected by both the annealing temperature and plastic strain.
Keywords:
Grain Size, Annealing, Static Recrystallization, Grain Growth, FEM

1. Introduction
The advantages of pure aluminum make it particularly appropriate for intricate forming processes by virtue of its high ductility and the ideal ratio of Young’s modulus to mass density especially as the grain size is reduced [1] .
Many important mechanical properties of materials, including yield strength, hardness and toughness can be improved by refining the grain size. Cold working (CW) and then annealing at recrystallization temperatures are the fundamental phenomena of microstructure evolution in the processing of engineering materials such as aluminum alloys for achieving to desirable grain size. When a new grain is nucleated during processing (as in annealing after cold working), the atoms within each growing grain, are lined up in a specific pattern that depends upon the crystal structure of the metal or alloy. With growth, each grain will eventually impinge on others and form an interface where the atomic orientations are different. Therefore, processing conditions must be carefully controlled to obtain the desired grain size and microstructure and to avoid the undesirable or abnormal grain growth. The free energy of a crystalline material is raised during deformation by the presence of dislocations and interfaces and a material containing these defects is thermodynamically unstable. If the material is subsequently heated to a high temperature (annealed) thermally activated processes such as solid state diffusion provide mechanisms whereby the defects may be removed or alternatively arranged in configurations of lower energy [2] . On annealing a cold deformed metal at an elevated temperature, the microstructure and also the mechanical properties may be partially or completely restored by recovery (in which rearrangement of the dislocations occurs) or recrystallization (in which new dislocation-free grains are formed within the deformed material) respectively. Further annealing may result in grain growth, in which the smaller grains are eliminated, the larger grains grow, and the grain boundaries assume a lower energy configuration.
In the common case of deformation at ambient temperature almost all of the stored energy is derived from the accumulation of dislocations and the essential difference between the deformed and the annealed states lies in the dislocation content and arrangement. In aluminum alloys, especially in alloys not hardened by precipitates, the most important transformation process, resulting in specific microstructures determining material strength and formability, is recrystallization [3] - [7] .
Lin et al. [8] proposed the kinetic equations to predict the static recrystallization behaviors of hot deformed 42CrMo steel. Takaki and Tomita [9] simulated the plastic deformation of the polycrystalline metal by the finite element method based on crystal plasticity theory and the microstructure evolution during recrystallization by the multi-phase-field method. Toloui and Serajzadeh [10] investigated the subsequent microstructural changes after hot deformation by employed the additivity rule and Avrami type equation to predict the kinetics of static recrystallization. Much research has been carried out to predict the microstructural evolution with the use of artificial neural network (ANN) and FEM [11] - [17] . Lin et al. [11] have studied the effects of the deformation temperature, strain rate and amount of deformation, as well as initial grain sizes, on the static recrystallization behaviors by using the experiments and ANN model. Previous study of the microstructural evolution of aluminum alloys have involved isothermal static recrystallization by means of quantitative microscopy [17] , the recrystallization kinetics of a 90% cold-rolled AA1050 by use of 3-dimensional X-ray diffraction microscopy [18] [19] . Nielsen et al. [20] measured the growth of individual grains in aluminium alloy of AA5182 in situ during a recrystallization heat treatment. Kim et al. [21] studied grain growth in aluminium alloy samples with two different recrystallization textures. The modeling and simulation of aluminium alloys during extrusion processes was carried out by Parvizian et al. [22] . They considered a number of aspects of the structural simulation as well as that of extrusion as a thermomechanical process.
In this investigation, the static recrystallization and grain growth behavior of cold-worked commercial purity aluminium has been studied by using experimental and numerical results at various isothermal annealing conditions. The influence of different parameters such as temperature and holding time of isothermal annealing and amount of the cold work performed, on the microstructure evolution have been investigated. The main attention of this paper is concentrated on development of recrystallization and grain growth equations and consequently predicting and controlling the material microstructural behavior especially grain size at different processing conditions.
2. Recrystallization and Grain Growth
Recrystallization and grain growth are the main phenomena occurring during annealing. The driving force for both recovery and recrystallization can be obtained by increasing of dislocation density and the stored energy of cold-work. Whereas the microstructure still contains grain boundaries that are thermodynamically unstable, although recrystallization removes the dislocations. If the new dislocation-free grains are heated at a temperature greater or for holding time more than which required to cause recrystallization, there will be a progressive increase in grain size. Therefore further annealing may result in grain growth, in which the smaller grains are eli- minated, and amount of the grain boundary decreases so the grain boundaries take a lower energy configuration [23] [24] . Recrystallization and grain growth, which studied in this investigation, are softening mechanisms that alter the microstructure without necessarily altering the phase.
2.1. Kinetics of Static Recrystallization (SRX)
The main variables that influence SRX behaviour are initial grain size , composition and impurities, pre cold-worked values
, composition and impurities, pre cold-worked values , especially temperature
, especially temperature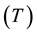 , holding time
, holding time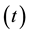 , the cold working method (compression, rolling, drawing, etc.), and amount of recovery prior to the start of SRX (which depend on stacking fault energy of material). The temperature at which recrystallization occurs depends on other mentioned parameters such as chemical composition, initial grain size, strain, the holding time of annealing, etc.
, the cold working method (compression, rolling, drawing, etc.), and amount of recovery prior to the start of SRX (which depend on stacking fault energy of material). The temperature at which recrystallization occurs depends on other mentioned parameters such as chemical composition, initial grain size, strain, the holding time of annealing, etc.
The theoretical model that based on a modified form of the classic Johnson-Mehl-Avrami-Kolmogorov (JMAK) equation has been used for obtaining recrystallized volume fraction (Equation (1)) [25] .
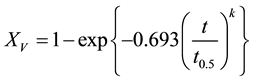 (1)
(1)
where 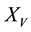 represents the static recrystallized volume fraction achieved at the annealing temperature,
represents the static recrystallized volume fraction achieved at the annealing temperature, 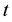 is annealing time,
is annealing time, 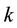 is the Avrami exponent and
is the Avrami exponent and  is the time corresponding to a 50% static recrystallized volume fraction that mathematically expressed as Equation (2).
is the time corresponding to a 50% static recrystallized volume fraction that mathematically expressed as Equation (2).
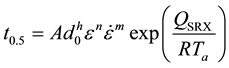 (2)
(2)
In this equation, 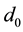 is the initial grain size before starting of static recrystallization,
is the initial grain size before starting of static recrystallization,  and
and 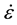 are applied strain and strain rate during cold working respectively, Ta is the annealing temperature, QSRX is the activation energy of SRX,
are applied strain and strain rate during cold working respectively, Ta is the annealing temperature, QSRX is the activation energy of SRX, 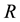 is the universal gas constant (8.3144 J∙mol−1∙K−1),
is the universal gas constant (8.3144 J∙mol−1∙K−1), 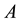 ,
, 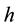 ,
, 



where, 



The recrystallization evolution can be measured by several methods, such as calorimetry, measurements of density, electrical resistivity, hardness and proof stress. However, the structural changes expressed in the pro- perty changes are often small and difficult to measure. So, the polarized light microscopy (PLM) is an essential and accurate method for the investigation of the recrystallization of aluminum alloys [26] .
2.2. Grain Growth
When primary recrystallization is complete the structure is not yet stable, and further growth of the recrystallized grains may occur if the high temperature is maintained. The driving force for this is a reduction in the surface energy which is stored in the material in the form of grain boundaries. During the normal grain growth, curved boundaries migrate frequently towards the centers of curvature; therefore the relative large grains will grow up by means of consuming the small neighboring grains. But the growing grains could be consumed either if they have touched a larger grain. If it holds that the rate of growth is proportional to the driving force and that the driving force is proportional to the total amount of grain boundary energy, then it can be shown that the holding time t required to reach a given grain size is approximated by Equation (4).

where 






3. Materials and Experimental Procedure
3.1. Material and Sample Preparation
The chemical composition of the commercial pure aluminum (AA1070) employed in this work is given in Table 1. The rod samples with diameter of 16 mm were hot extruded of the initial samples of AA1070.
Table 1. Chemical composition (wt%) of AA1070.
3.2. Cold Working Conditions
The investigations show that the prior deformation applied to the material must be adequate to provide nuclei and sufficient stored energy to drive their growth. So a critical deformation (cold working) required for the beginning of recrystallization. Therefore pre-cold-worked values are other important parameters that influence the recrystallization and grain growth behaviors of metals. In this study, as shown in Table 2, the hot extruded samples have been cold drawn for different values of reduction consisting of 23.44%, 43.75%, 60.94% and 75%. Cylindrical samples with the height to diameter ratio of 1.5 were machined out of the drawn bars with the longitude axis parallel to the drawing direction. Average linear grain intercept lengths technique was used for grain size determination of annealed samples. They electrolytically anodizes using combination of Barker’s reagent and HF (4 ml HBF4 + 0.5 ml HF and 200 ml H2O) with applying of direct electrical current of 20 V for 70 s. This technique is mainly issued for the study of the initial stages of recovery and recrystallization [27] .
Figure 1 shows the microstructure of hot extruded sample of AA1070 before cold working. Whereas, Figure 2 shows the microstructures of cold drawn AA1070 with different degrees of cold drawing at 23.44%, 43.75%, 60.94% and 75%, respectively. As it is clear from Figures 2(a)-(d), with increase in the percentage of cold deformation, the grains become more elongated in the drawing direction.
3.3. Annealing Conditions
Annealing heat treatment was used to SRX and grain growth evolution. Investigations indicate that temperature has the most significant effect on the recrystallization and grain growth. In this investigation, annealing temperatures of 350˚C, 450˚C and 600˚C in different ranges of holding time have been studied. Microstructural observations of PLM can be applied to determine necessary temperature and holding time for recrystallization and grain growth.
4. Finite Element Simulation
In this way, a cold drawing model has been constructed to simulate a single pass of the cold rod drawing process for the AA1070 using the commercial FE software package, DEFORMTM. Figure 3 shows strain distribution and mesh distortion during cold drawing of AA1070 for a reduction of 70% and initial diameter of the rod of 16 mm. As it is clear, the strain distribution in the various regions of the rod is not uniform and strain variations of the surface region are more than of the central regions, and the maximum value of strain (1.6) will occur in the surface region of rod.
5. Results and Discussion
5.1. Static Recrystallization
The investigations show that annealing temperatures under 320˚C do not have sensible holding time for recrystallization; therefore theses temperatures cannot be a proper recrystallization temperature for this material. So the recrystallization temperature is higher than 320˚C for this material and in this condition of cold drawing. The experimental results and observations of PLM show that the SRX volume fraction has been increased by increasing of holding time at each temperature that is over than 320˚C. For example, Figures 4(a)-(d) show the different volume fraction of SRX 
As it is expected, the amount of 
Figure 1. PLM microstructure of AA1070 polycrystalline specimen before cold working.


Figure 2. PLM microstructure of AA1070 after cold working at different reductions of (a) 23.44%; (b) 43.75%; (c) 60.94% and (d) 75%.
Figure 3. Mesh distortion and strain distribution during cold drawing of AA1070 for a reduction of 70% and initial diameter of the rod of 16 mm.


Figure 4. Microstructural changing of cold drawn (Ra = 75%) AA1070 at annealing temperature of 450˚C and holding times of (a) 120 sec; (b) 200 sec; (c) 280 sec and (d) 360 sec.
Table 2. Cold working stages.

Therefore 

where


ship between the required holding time for recrystallization of 50% and annealing temperature, as shown in Figure 5. With considering that the annealing process is carried out at constant value of reduction

The values of 



Following the same procedure, the strain exponent 


where;


tionship between the time required for recrystallization of 50% and the value of cold working, as shown in Figure 6. With considering that the annealing process is carried out at constant annealing temperature

Hence, the values of 



With regard to the initial deformation isn’t at high temperature, so the effect of strain rate is relatively insignificant; and the strain rate exponent 
In order to verify the accuracy of developed equation of SRX of AA1070 at annealing conditions, a comparison between the experimental and predicted results was carried out as shown in Figure 8 and Figure 9.
Figure 5. Evaluating the value of 

Figure 6. Evaluating the value of n by fitting
Figure 7. The influence of annealing temperature on the Avrami exponent at different reductions.
Figure 8. Comparisons between measured and predicated values of static recrystallized fraction of AA1070 at annealing temperature of 450˚C and different values of reduction.
Figure 9. Comparisons between measured and predicated values of static recrystallized fraction of AA1070 at cold work reduction value of 60.94 percent and different annealing temperature.
It could be observed that the predicted SRX value from the developed equation could track the experimental data throughout the entire annealing time range and for different reductions and annealing temperatures. As it is clear, the volume fraction of SRX depends on the amount of applied cold work as a higher amount of cold work translates to a lower time of full recrystallization.
5.2. Grain Growth
The material constants of grain growth equation (Equation (4)) that obtained by experimental results have been presented in Table 3 for AA1070. So Equation (4) can be used for computing of grain size of the recrystallized AA1070. As it is clear from Figure 10, the predicted grain size from this equation could track the experimental data throughout the entire holding time range and there are good agreements between the results of the predicated and experimental data.
The results show that the final grain size increases with increasing of the holding time and strongly annealing temperature. Moreover, it is observed in this Figure 10 that the essential grain growth is concentrated in the beginning of holding time, and grain growth rate gradually decreases with increasing of holding time. In the other
Figure 10. Comparisons between measured and predicated grain size curves of AA1070.
Table 3. The experimental values of the material constants at different temperatures.
word, with increasing of holding time from a particular value, the grain size will not sensibly increase. Also, it is clear that grain size increases by increased cold work reduction at the specific holding time and temperature.
Figure 11 demonstrates the effects of holding time on grain growth and grain size of AA1070 at annealing temperature of 550˚C, with initial cold deformation of 60.94%. As it is clear, the average grain size increases from 70 to 180 μm with increasing holding time from 15 min to 120 min, respectively.
5.3. Numerical Results and Experimental Validation
The developed equations of recrystallization and grain growth were employed in finite element analysis. Using FEM computations, volume fraction of SRX and grain growth evolution were predicted. For this purpose, the effects of various processing parameters were considered and the annealing conditions were simulated. Simulation of the cold drawing process at a different initial cold work (reduction of 75%), for which the experimental results were not used in order to derive the equations for recrystallization and grain growth, can be useful for validation of simulation model and applied equations. Figure 12 shows FEM results of volume fraction of SRX at annealing temperature of 450˚C of cold drawn AA1070 (reduction of 70%) after holding time of 160 sec. The simulation results of grain size resulted of grain growth at different holding time of 900 sec to 7200 sec has been displayed in Figure 13. As it is clear from this figure, the grain size value is increased when holding time is increased during grain growth.
In order to estimate the reliability of this FE model, a comparison was made between the time for 50% static recrystallization predicted by simulations and the experimental results data of the cold drawn (Ra = 75%) of AA1070.
It is clear from Figure 14 that the results of time for 50% SRX of the experimental data and simulation have


Figure 11. PLM microstructure of AA1070 at annealing temperature of 550˚C and holding times of (a) 15 min; (b) 30 min; (c) 90 min and (d) 120 min (Ra = 60.94%).
Figure 12. Volume fraction of static recrystallization during annealing after 160 sec holding time at annealing temperature of 450˚C of cold drawn AA1070 (reduction of 70%).

Figure 13. Grain size of cold drawn AA1070 (reduction of 70%) during grain growth after (a) 900 sec; (b) 1800 sec; (c) 3600 sec and (d) 7200 sec holding time at annealing temperature of 450˚C.
Figure 14. Comparison of numerical and experimental results of the time of 50% static recrystallization (Ra = 75%) with different annealing temperature.
proper accordance by varying annealing temperature. As can be seen, the difference between simulation and experimental results are 2.42%, 5.08% and 9.2% for 350˚C, 450˚C and 600˚C, respectively.
Finally, it can be claimed that the developed equations of recrystallization and grain growth can be used to numerically simulate the annealing process of AA1070 aluminum alloy and can be used to analyze the problems during recrystallization process.
6. Conclusions
In this study, microstructural variation of cold-worked AA1070 aluminum alloy was predicated during annealing by isothermal heat treatment over wide ranges of temperatures and holding time. Following are the conclusions:
The earlier cold deformation applied to the material must be adequate to provide nuclei and sufficient stored energy to drive their growth. So a critical deformation (cold working) is required for the beginning of recrystallization.
The results show that temperature has significant influence on the recrystallization and there is a critical value of temperature for initiation of recrystallization that depends on the amount of cold work, as a higher amount of cold work translates to a lower temperature of recrystallization.
The developed equations were found to predict recrystallization and grain growth precisely at all of the annealing temperature range, holding time and cold deformation amount.
Finally, the results of simulations show that the developed equations give a precise estimate for the recrystallization and grain growth and can be used to numerically simulate the annealing process of cold-worked AA1070 aluminum alloy. So, these developed equations and simulation finite element models can accurately predicate the microstructural variation of cold-worked pure aluminum during annealing process.
References
- Totten, G.E. and MacKenzie, D.S. (2003) Handbook of Aluminium. In: Physical Metallurgy and Processes, Marcel Dekker, New York, 66-73.
- Humphrey, F.J. and Hatherly, M. (2004) Recrystallization and Related Annealing Phenomena. Elsevier Ltd., Oxford.
- McQueen, H.J. and Blume, W. (1998) Recovery and Recrystallization in Al Alloys: Fundamentals and Practical Applications. In: Sato, T., Kumai, S., Kobayashi, T. and Murakami, Y., Eds., Proceedings of the 6th International Conference on Aluminum Alloys (ICAA6), Japan Institute of Light Metals, Tokyo, 99-112.
- Saeter, J.A., Forbord, B., Vatne, H.E. and Nes, E. (1998) Modelling Recovery and Recrystallization, Applied to Back- Annealing of Aluminium Sheet Alloys. In: Sato, T., Kumai, S., Kobayashi, T. and Murakami, Y., Eds., Proceedings of the 6th International Conference on Aluminum Alloys (ICAA6), Japan Institute of Light Metals, Tokyo, 113-126.
- Humphreys, F.J. (1999) A New Analysis of Recovery, Recrystallization and Grain Growth. Materials Science and Technology, 15, 37-44. http://dx.doi.org/10.1179/026708399773002791
- Orsetti Rossi, P.L. and Sellars, C.M. (1997) Quantitative Metallography of Recrystallization. Acta Materialia, 45, 137-148. http://dx.doi.org/10.1016/S1359-6454(96)00167-X
- Vandermeer, R.A. and Jensen, D.J. (2001) Microstructural Path and Temperature Dependence of Recrystallization in Commercial Aluminum. Acta Materialia, 49, 2083-2094. http://dx.doi.org/10.1016/S1359-6454(01)00074-X
- Lin, Y.C., Chen, M.S. and Zhong, J. (2008) Study of Static Recrystallization Kinetics in a Low Alloy Steel. Computational Materials Science, 44, 316-321. http://dx.doi.org/10.1016/j.commatsci.2008.03.027
- Takaki, T. and Tomita, Y. (2010) Static Recrystallization Simulations Starting from Predicted Deformation Microstructure by Coupling Multi-Phase-Field Method and Finite Element Method Based on Crystal Plasticity. International Journal of Mechanical Sciences, 52, 320-328. http://dx.doi.org/10.1016/j.ijmecsci.2009.09.037
- Toloui, M. and Serajzadeh, S. (2007) Modelling Recrystallization Kinetics during Hot Rolling of AA5083. Journal of Materials Processing Technology, 184, 345-353. http://dx.doi.org/10.1016/j.jmatprotec.2006.11.227
- Lin, Y.C., Liu, G., Chen, M.S. and Zhong, J. (2009) Prediction of Static Recrystallization in a Multi-Pass Hot Deformed Low-Alloy Steel Using Artificial Neural Network. Journal of Materials Processing Technology, 209, 4611- 4616. http://dx.doi.org/10.1016/j.jmatprotec.2008.10.020
- Seyed Salehi, M. and Serajzadeh, S. (2010) A Neural Network Model for Prediction of Static Recrystallization Kinetics under Non-Isothermal Conditions. Journal of Materials Processing Technology, 49, 773-781. http://dx.doi.org/10.1016/j.commatsci.2010.06.021
- Seyed Salehi, M. and Serajzadeh, S. (2012) Simulation of Static Recrystallization in Non-Isothermal Annealing Using a Coupled Cellular Automata and Finite Element Model. Computational Materials Science, 53, 145-152. http://dx.doi.org/10.1016/j.commatsci.2011.09.026
- Cho, J.R., Jeong, H.S., Cha, D.J., Bae, W.B. and Lee, J.W. (2005) Prediction of Microstructural Evolution and Recrystallization Behaviors of a Hot Working Die Steel by FEM. Journal of Materials Processing Technology, 160, 1-8. http://dx.doi.org/10.1016/j.jmatprotec.2004.01.001
- Wang, K.L., Fu, M.W., Lu, S.Q. and Li, X. (2011) Study of the Dynamic Recrystallization of Ti-6.5Al-3.5Mo-1.5Zr- 0.3Si Alloy in β-Forging Process via Finite Element Method Modeling and Microstructure Characterization. Materials & Design, 32, 1283-1291. http://dx.doi.org/10.1016/j.matdes.2010.09.033
- Serajzadeh, S. (2007) A Study on Kinetics of Static and Metadynamic Recrystallization during Hot Rolling. Materials Science and Engineering: A, 448, 146-153. http://dx.doi.org/10.1016/j.msea.2006.10.070
- Vandermeer, R.A. and Juul Jensen, D. (2003) Recrystallization in Hot vs Cold Deformed Commercial Aluminum: A Microstructure Path Comparison. Acta Materialia, 51, 3005-3018. http://dx.doi.org/10.1016/S1359-6454(03)00112-5
- Lauridsen, E.M., Poulsen, H.F., Nielsen, S.F. and Juul Jensen, D. (2003) Recrystallization Kinetics of Individual Bulk Grains in 90% Cold-Rolled Aluminium. Acta Materialia, 51, 4423-4435. http://dx.doi.org/10.1016/S1359-6454(03)00278-7
- Poulsen, S.O., Lauridsen, E.M., Lyckegaard, A., Oddershede, J., Gundlach, C., Curfs, C. and Juul Jensen, D. (2011) In Situ Measurements of Growth Rates and Grain-Averaged Activation Energies of Individual Grains during Recrystallization of 50% Cold-Rolled Aluminium. Scripta Materialia, 64, 1003-1006. http://dx.doi.org/10.1016/j.scriptamat.2011.01.046
- Nielsen, S.F., Schmidt, S., Lauridsen, E.M., Yiu, H., Savoie, J., Zeng, M. and Juul Jensen, D. (2003) Growth Kinetics of Individual Grains during Recrystallization with an Intermediate Cooling Cycle. Scripta Materialia, 48, 513-518. http://dx.doi.org/10.1016/S1359-6462(02)00499-2
- Kim, H.C., Kang, C.G, Huh, M.Y. and Engler, O. (2007) Effect of Primary Recrystallization Texture on Abnormal Grain Growth in an Aluminum Alloy. Scripta Materialia, 57, 325-327. http://dx.doi.org/10.1016/j.scriptamat.2007.04.023
- Parvizian, F., Kayser, T., Hortig, C. and Svendsen, B. (2009) Thermomechanical Modeling and Simulation of Aluminum Alloy Behavior during Extrusion and Cooling. Journal of Materials Processing Technology, 209, 876-883. http://dx.doi.org/10.1016/j.jmatprotec.2008.02.076
- Huang, Y.D. and Froyen, L. (2002) Recovery, Recrystallization and Grain Growth in Fe3Al-Based Alloys. Intermetallics, 10, 473-484. http://dx.doi.org/10.1016/S0966-9795(02)00019-5
- Zhang, J.M., Gao, Z.Y., Zhuang, J.Y. and Zhong, Z.Y. (2000) Grain Growth Model of IN718 during Holding Period after Hot Deformation. Journal of Materials Processing Technology, 101, 25-30. http://dx.doi.org/10.1016/S0924-0136(99)00437-9
- Puchi Cabrera, E.S., Villalobos Gutierrez, C.J., Carrillo, A. and DiSimone, F. (2003) Non-Isothermal Annealing of a Cold Rolled Commercial Twin Roll Cast 3003 Aluminum Alloy. Journal of Materials Engineering and Performance, 12, 261-271. http://dx.doi.org/10.1361/105994903770343105
- Slamova, M., Ocenasek, V. and Vander Voort, G. (2004) Polarized Light Microscopy: Utilization in the Investigation of the Recrystallization of Aluminum Alloys. Materials Characterization, 52, 165-177. http://dx.doi.org/10.1016/j.matchar.2003.10.010
- Rezaei Ashtiani, H.R., Parsa, M.H. and Bisadi, H. (2012) Effects of Initial Grain Size on Hot Deformation Behavior of Commercial Pure Aluminum. Materials & Design, 42, 478-485. http://dx.doi.org/10.1016/j.matdes.2012.06.021
NOTES
*Corresponding author.



















