Modeling and Numerical Simulation of Material Science
Vol.04 No.03(2014), Article ID:47693,14 pages
10.4236/mnsms.2014.43010
Immersive 3D Visualization of the Collective Behavior of Particles and Crystal Dislocations Using Virtual Reality Technology
Smruti R. Panigrahi1, Sankar Jayaram2, Uma Jayaram2, Hussein M. Zbib2, Sinisa Dj. Mesarovic2
1Department of Mechanical Engineering, Michigan State University, East Lansing, USA
2School of Mechanical and Materials Engineering, Washington State University, Pullman, USA
Email: smruti@msu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 April 2014; revised 2 May 2014; accepted 2 June 2014
ABSTRACT
In this article, we present a three-dimensional visualization technique that has been developed in order to establish an interactive immersive environment to visualize the particles in granular materials and dislocations in crystals. Simple elementary objects often exhibit complex collective behavior. Understanding of such behaviors and developments of coarse-scale theories, often re- quires insight into collective behavior that can only be obtained through immersive visualization. By displaying the computational results in a virtual environment with three-dimensional percep- tion, one can immerse inside the model and analyze the intricate and very complex behavior of in- dividual particles and dislocations. We built the stereographic images of the models using OpenGL rendering technique and then combine with the Virtual Reality technology in order to immerse in the three-dimensional model. A head mounted display has been used to allow the user to immerse inside the models and a flock of birds tracking device that allows the movements around and within the immersive environment.
Keywords:
Virtual Reality, Telepresence, 3D Stereographic Visualization, OpenGL Rendering, Grain Simulation, Delaunay Network, Dislocation Dynamics

1. Introduction
Virtual reality (VR) is an emerging technology that provides users with realistic, computer simulated interactive three-dimensional (3D) environment in which people become immersed [1] [2] . VR provides high interactivity, which is achieved when users are provided with immediate feedback through their perceptions that a mediated environment is modified, based on their input [3] . This relates to the prominent features of VR. VR interfaces provide high-quality 3D images of products, interactivity with the products, and increased telepresence [3] [4] .
Telepresence is a sense of “being there” in an environment by means of a communication medium [4] [5] . Based upon sensory stimuli conveyed by a VR interface, human beings can create a perceptual illusion of being present and highly engaged in a mediated environment, while they are in reality physically present in another place [6] . VR also have significant effects on learning process [7] [8] .
There have been ongoing attempts by researchers in bringing virtual models to life with better visualization and interaction techniques [9] -[11] using various VR devices such as Flock of Birds, Cyber Gloves, Cyber Grasps, Head-Mounted Displays, and Force Feedback Devices such as PHANTOM Devices. With new ideas, incorporated with advanced equipment, and years of evolution, many have successfully implemented various fascinating applications. VR has evolved through many years of research in hardware and software technologies and applications. In this research, we use VR technology for the visualization of the granular materials and dis- locations in crystals.
For the immersive grain visualization it is very important to understand the dynamics of the individual grain as well as their collective behavior in the presence of a grain cluster and applied shear. From the mechanics perspective, this involves understanding of the governing equations for position, orientation, velocity, accelera- tion, and the contact forces between the grains [12] . The forces in a granular media in a confined vessel due to auni-axial compression are distributed onto the interior surfaces of the confined boundary [13] . Spatial packing order and interparticle friction in a large hexagonal close packed crystal, affect directly the distributions of nor- mal forces in a three-dimensional granular media [14] .
Extensive research has been done in an effort to understand various dynamics of grain interactions [15] -[21] . Granular flows consisting of about a million particles are visualized in 3D, using parallel discrete element me- thod (DEM) simulation [22] . DEM is a family of numerical methods for computing the motion of a large num- ber of particles like molecules or grains of sand [23] . Various types of rotations at different scales, for example the rotations of individual particles, the rolling and rigid-rotation of particle pairs, the rotational interactions of a particle within its cluster of neighbors, and the rotation of material regions are studied using numerical DEM simulations on two- and three-dimensional granular assemblies [24] .
Understanding the dynamics of dislocations and its propagation is important in order to create visualization models for the same. Topology of dislocation propagation [25] and real time interactive visualization of three- dimensional molecular dynamic models for dislocation nucleation and dislocation dynamics by a potential energy mapping algorithm [26] has been studied. Numerical techniques have been developed by various authors [27] -[32] for the evaluation and visualization of dislocation accumulation in various crystals. The authors have analyzed the plastic slip deformation of crystals and metal microstructures by finite element methods and eva- luated the developments of dislocation density distribution in conjunction with gradients of plastic shear strain on crystal slip systems. These continuing researches lay out our current understanding of the dynamics behind the dislocations in crystals.
The dynamics of the dislocations under applied load is evolved according to physical laws, yielding a set of differential equations, which are solved numerically. The output from these simulations, among other thing, is the spatial distribution of the dislocation curves for each time step. Because of their interactions, dislocation curves tend to develop into low energy configurations (see examples in [33] ). A dislocation dynamics model, named micro3d, has been developed in which the dislocations are represented as discrete segments in a three-dimensional (3D) crystalline space [28] . Detecting these 3D structures is not trivial and, therefore, visuali- zation becomes important in order to identify reactions among the various dislocation curves and to identifying structures.
We see significant contributions from many researchers in modeling and visualizing the particle behavior in granular media and the dislocations. There has been tremendous work done using the DEM for the simulation of granular flows. Many researchers have done the visualization of the dislocations using continuum mechanics analysis. However, there has been no research in visualizing the granular assembly and dislocations in materials using VR technology. Our hypothesis is that by using OpenGL rendering technique and combining VR technol- ogy with the mathematical simulations of the granular flow as well as crystal dislocations, researchers will have greater insight and a better understanding of the complex mathematical models using the sense of visual stimu- lus provided by the telepresence.
2. Motivations and Mathematical Model
Our goal is to create 3D stereographic and immersive visualizations of three different types of models, (a) gra- nular assembly, (b) Delaunay network of the granular assembly, and (c) dynamics in crystal dislocations.
In the granular assembly as well as the crystal dislocations, the positions and orientations of the grains (Fig- ure 1) and dislocations are calculated according to the fundamental laws of physics using the force and momen- tum as
 (1)
(1)
 (2)
(2)
where 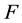 and
and 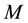 are the force and angular momentum,
are the force and angular momentum,  is the mass,
is the mass, 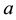 is the acceleration,
is the acceleration, 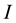 is the moment of inertia, and
is the moment of inertia, and  is the angular velocity.
is the angular velocity.
In the granular assembly, the force 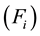 and angular momentum
and angular momentum 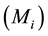 on particle
on particle  is
is
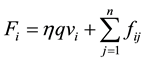 (3)
(3)
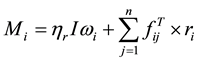 (4)
(4)
where 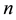 is the total number of particles interacting with the reference particle,
is the total number of particles interacting with the reference particle, 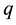 is the viscous regularization of Coulomb’s friction law, and
is the viscous regularization of Coulomb’s friction law, and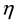 ,
, 








where


The force vector 
Figure 1. Identical spherical particles of radius rc in contact.
ticles are calculated by the mathematical model at each time step by the application of above laws in Equations (3), (4), and (5). We find a similarity in the mechanics of the problems for both grain structures and dislocations simulation.
3. Problem Definition and User Requirements
For the granular assembly and Delaunay network the goal is to visualize the behavior of the individual particles under application of axial shear strain. The assembly of granules is assumed to be contained in an elastic mem- brane immersed in a fluid as shown in Figure 2. The axial strain rate 

Each granule is treated as a discrete entity and its interaction with other particles forms the mechanics of the problem that we have discussed in previous section. In the grain structures, we visualize the position, orientation and motion of individual grains. In our visualization model we render the grain particles as solid spheres and then create the Delaunay network of the grain assembly. The Delaunay network is a collection of tetrahedrons that are formed by connecting the centers of neighboring grains. Visualization of the Delaunay network provide more clear information about the grains which are in actual contact that we refer to as TRUE contacts and which are not in contact that we refer to as FALSE contacts.
For dislocations, the goal is to be able to visualize the formation and movements of dislocations to understand transient dynamics of the dislocation mechanisms by taking advantage of the depth perception.
3.1. Scope of Work
Scope of work for this research includes understanding the visualization techniques using OpenGL and integrat- ing it with virtual reality technology in order to form a telepresence and implementing that into the above-men- tioned problems to build a more meaningful 3D visualization.
For granular assembly we hypothesize to create methods to visualize 3D animations of grain behavior, and immerse in the granular layer to enable walking inside the model for visualization of the transient dynamics of individual particles.
For the Delaunay network we hypothesize to create a 3D visualization model for the Delaunay network of
Figure 2. Assembly of granules under an axial strainrate in presence of hudrostatic pressure P.
the granular assembly, to distinguish between the TRUE and FALSE contacts between the particles of the grain assembly and to show the breakage of the existing contacts, formation of new contacts and to walk in- side the model to visualize the transient behavior of the interior contacts of individual particles
For the dislocations we hypothesize to create methods to enable immersive 3D visualization of the dislo- cations and its propagation inside the network to easily identify and track the transient dynamics of the propagating, non-propagating or stationary dislocations, and the dislocations in different slip planes.
3.2. User Requirements
We formulate and lay out specific requirements that will be addressed in our 3D simulations and VR experi- ments. The following are the user requirements.
Visualize the simulations in 3D and use zoom, pan and rotate to view the simulation models from various orientations.
Distinguish between smaller and larger grains as well as TRUE and FALSE contacts in the Delaunay tetra- hedral structure.
Visualize the formation and breakage of contacts in the Delaunay network, and the real time dynamics of the TRUE and FALSE contacts with the applied strain and pressure.
Distinguish between different slip planes in the dislocations model as well as the difference between statio- nary and propagating dislocations.
Build a telepresence for all three models, to show a 3D stereographic simulation with depth perception and to be immersed inside the model to walk around and within the model investigate the behavior of the particles and dislocations.
4. Methods and Algorithms
In the first stage of visualization, we have used the OpenGL rendering technique to build a 3D model to observe the transient dynamics of the granular assembly and the crystal dislocations using the data from numerical solu- tions. We then implement the stereographic visualization using two projectors and a 3D glass. Then we integrate the models with VR technology by implementing, the VR devices, head-mounted display and flock of birds tracking device. Head mounted display has been used to immerse inside the model, and the flock of birds as the tracking device to ensure a telepresence in the virtual 3D model.
Using computational methods we first obtain the transient locations and orientation information for the grain particles and crystal dislocations. We save these information in various data files. We render the models by reading the data files in text format and updating the data files in each frame for the purpose of simulation. The data files are created by solving for the differential equations of the displacement and rotations in MATLAB. These data files consist of the location information for Dislocations and the location, orientation, velocity, ace- leration, angular velocity, and angular acceleration information of individual particles in the granular assembly for each time step. Here time step is a small increment in time that we consider to get the particle location and orientation information as the assembly is going through the strain and pressure to obtain transient information. The data files in case of the Delaunay network consist of the connected grain numbers or indices of a tetrahe- dral.
Following sub-sections describe the algorithms used to render in 3D as well as in immersive VR environment. A general algorithm for rendering process in OpenGL is shown in Figure 3. We implement the keyboard and mouse functionality to navigate around the simulated model in the virtual environment. “OpenGL rendering of the nth data file” step of the flowchart in Figure 3 represent an image of the locations and orientations of all the particles ordislocations in the assembly at a particular time step. These locations and orientations information are obtained from the data file created from the numerical simulation of the transient dynamics.
4.1. Rendering of Granular Assembly
The overall algorithm for the rendering of the granular assembly follows the flowchart shown in Figure 3. In our case there are 40 (N = 40) different time steps considered to represent the transient states of the grain assem- bly. This number, N, can be changed according to the number of input data files available for the visualization code. Different data files correspond to different time steps during the process of the numerical simulation of the particle dynamics [11] .
Figure 3. Algorithm for the OenGL rendering process.
Here we use spheres to represent the grains. We have used a threshold characteristic radius of 0.75 to differ- rentiate between large and small grains. However, the grain assembly contains many different sized particles. The size of the particles has been calculated using a random number generator scheme [11] .
4.2. Delaunay Network Rendering
Delaunay network is a good way of visualizing the actual interactions of a particular grain with its surrounding particles. Here we use a line representation to connect the center of any two granular spheres. There are two types of links, namely TRUE and FALSE contacts that can be formed between any two spheres according to their radius and relative distance from each other [11] .
We form a tetrahedron link list by taking four spheres that fall into the nearest neighbor group using an exist- ing code called “tetgen”, which can be found on the web [34] . Then we use this data to render the tetrahedrons using OpenGL algorithm shown in Figure 3 by connecting the centers of the grains and representing the con- nection as straight lines. Some sample data can be found in the Appendix.
4.3. Rendering of Crystal Dislocations
For the visualization of the crystal dislocations, we use the same algorithm as in Figure 3. Here the data files were generated by software called “techplot”. We represent a line between any two points by the vector pro- vided by the techplot data file. We also apply different colors to different slip planes of the dislocations. Here we have only four types of color index that we apply the techplot data file where each color code represents a sepa- rate slip-plane.
The data file provided by the techplot contains the position and color index of the each dislocation at different frames. Here we read the data file until the end of one frame (i.e. one time step) and then renders the lines. We keep the loop set to some predefined number of frames (N) and stop the rendering process once the desired number of loops is reached. For the user convenience the whole rendering process can be repeated as desired by pressing a key on the keyboard [11] .
5. VR Experimental Result
Depending on the extent of immersion, VR applications can be classified into two categories: immersive VR and non-immersive VR [35] . In the former, users wearing head-mounted displays are totally surrounded by enclosed virtual environments. Desktop or laptop computers, on the other hand, most commonly convey non-immersive VR. Thus, for users, VR experiences are limited to what they see on their display monitors and what they hear from their speakers. Generally most researchers use non-immersive visualization due to the high expense and cumbersome equipment required for immersive VR. However, this research focuses on both non-immersive and immersive VR interfaces to provide a better understanding of the granular flow and crystal dislocations. We have first implemented non-immersive VR to create a 3D stereographic environment with depth perception, and then use the VR devices to create the immersive environment [11] .
VR offers a high level of control over computer-mediated environments, both in terms of user abilities to ad- just the information according to their individual interests and concerns, and, in general, their ability to be active, rather than passive, in their engagement with the information [36] . Through high media richness and interactivi- ty, VR can generate compelling feelings of telepresence [3] [6] .
The experiments have been done in the VRCIM Lab [11] [37] using OpenGL rendering, projectors, polarized 3D glasses, and VR devices head-mounted display and flock-of-birds (Figure 4). First we created the algorithms to simulate the models using computer programming. Then we implemented the 3D stereographic visualization by using two projectors to project the same image in two different screens with a predefined offset value in order to visualize the computer models in 3D, with depth perception, using the polarized glasses. This stereographic visualization experiment in the lab, provided with a better visualization with depth perception. Next we con- ducted the experiment by integrating our OpenGL computer code to the VR devices head-mounted display to create an immersive environment. Then we used the VR device, flock-of-birds, in order to obtain the desired orientations of the 3D models for the immersed user to be able to investigate the transient dynamics of the de- sired particle or dislocation [11] .
This visualization technique enabled us to identify and fix the problems in the mathematical model itself for example in the granular assembly with unconstrained boundary or inappropriate boundary conditions. Initially we noticed that there were not enough boundary constraints in the model based on the particles flying outside the boundary during the simulation as shown in Figure 5. Our 3D visualization technique helped us to identify the problem and fix it. Figure 6 shows the simulations of the model after applying the appropriate boun-
Figure 4. A head-mounted display with the tracking device flock-of-birds for telepresence in the immersive environment.
Figure 5. Simulation of the granular assembly with unconstrained boundary. The grain particles are observed to be flying out of the bounding box due to the inappropriate boundary conditions. Though this grain assembly contains many different sized particles (the radii of the grains here are generated using a random number generator), for simplicity we have used only two different colors to represent them in the simulation. The gray particles represent the grains of radius greater than the characteristic radius 0.75 and the blue ones are of radius smaller than the characteristic radius 0.75.
dary conditions. Using the VR devices we were able to create the feeling of a telepresence which in-turn helped investigate the complicated dynamics of the grains on the outer boundary as well as the inner particles (for ex- ample the particles in the center of the 3D grain assembly), which otherwise is impossible to visualize using simple 3D visualization technique on a computer.
In order to understand the dynamic contact behavior of the grains in the assembly we built a simulation for the visualization of the Delaunay network that is created using the nearest neighboring grain particles. The TRUE and FALSE contacts are shown in Figure 7.
We have represented the dislocations lying on different slip planes in different colors to highlight the propa- gation of the dislocations. With this VR experiment we were able to visualize the destruction of dislocations and formation of new dislocations using the 3D immersive visualization technique. Visualization of the dislocations simulation is shown in Figure 8. Immersion using the head mounted display inside the virtual model helped us to quickly identify dislocations and slip planes. The flock of birds tracking device helped us to walk near the re- gions of interest and investigate the behavior of the dislocation’s propagation.
Figure 6. Simulation of the granular assembly with appropriate boundary conditions shows a closely packed grain assembly with the applied shear.
Figure 7. Simulation of the Delaunay network i.e. tetrahedral representation of the granular assembly corresponding to the grain simulation shown in Figure 6.
Figure 8. An intermediate snap-shot of the crystal dislocations simulation. The colors represent the dislocations lying in different slip-planes. There are four different slip-planes and the color codes red, white, blue, and green represent the dislocation propagation on those four slip-planes.
The user requirements have been fulfilled as we have successfully implemented the following:
Visualized the models in 3D using the OpenGL rendering technique and implemented the zoom, pan, and rotate feature in our visualization models.
Added the keyboard function to have the flexibility of repeating the entire simulation cycle, and to return to the initial position to re-run the simulation.
Used different colors to render various size grains as well as shown the TRUE contacts in thick black bold lines and the FALSE contacts as dashed blue lines in the Delaunay network.
In the Delaunay network simulation we see the breakage of existing contacts and formation of new contacts as the simulation progress. We also clearly identify the moving and stationary dislocations as well as de- struction of the current dislocations and formation of new ones using the VR devices in the laboratory.
Implemented color-coding to identify the dislocations lying in different slip planes. In particular we have four different slip planes, so we have used four different colors to show the dislocations corresponding to each plane.
In all of our models we have implemented the stereo mode using the OpenGL rendering technique to visual- ize them in 3D with a depth perception. We have used two different projectors to create one image for each eye with an offset to incorporate depth perception to the whole model. We have used the VR Devices head mounted display and the flock-of-birds tracking device to be immersed and walk around as well as inside the models.
6. Summary, Conclusions and Outlook
6.1. Summary and Conclusions
In this article, we have discussed the methods and algorithms to create an immersive 3D visualization of the grain structures, Delaunay networks of the granular assemblies, and the dislocations propagation using OpenGL stereographic visualization and Virtual Reality technology. Stereographic view using OpenGL gives us a depth perception to the 3D model and provides a more realistic visualization and provides opportunity to examine the transient behavior of each granule closely to investigate their behavior.
We visualized the dislocations simulation by rendering the dislocation lines where different color indices are used to represent the dislocations lying in different slip planes. This visualization method enables us to identify the formation of new dislocations and the dislocations lying in different slip planes. It enables us to be immersed in the dislocations as well and investigate more closely the precise behavior of the critical dislocation move- ments and eventually will help understand the transient dynamics of the crystals.
We have implemented the mouse and keyboard functionality to allow the user to zoom, pan, rotate, and vi- sualize the models from different orientations and regions of interest. We then integrate projectors and polarized 3D glasses to build a 3D visualization with depth perception, and integrate all three models with VR devices in order to be immersed and walk around the models [11] . A head mounted display was used to immerse the user inside the virtual model and then a flock of bird tracking device that enable the walking around and within the models to get a better visualization of the simulation process.
Finally we conclude that 3D visualization combined with the use of VR technology can provide a new revolu- tionary path to the future of the human interaction with the tiniest of particles, like grains. It enables us to vi- sualize, analyze, and interact with the granular materials as well as the dislocations propagation. In our research, we have fulfilled all of the user requirements that was defined in our scope of work to visualize the simulation of granular assembly and the dislocations in 3D using the OpenGL visualization tool and VR technology.
6.2. Future Work
There is a lot of potential for future work in this area for example modifying the dislocations interactively by using VR and analyzing its effects, visualizing the stress contours as it is seen in different finite element tools, and using a virtual hand to interact with the grains and dislocations. Haptic force feedback device can be used to improve the telepresence experience by inducing touch stimuli to feel the forces on the granular assembly and individual grains.
There is a potential improvement that can be done to experience the sliding, rolling and reaction forces on the grain surfaces using the PHANTOM force feedback device. Behavior of particles due to applied force can be examined even without doing any physical experiments by applying the required force to our VR model by us- ing the PHANTOM force feedback device. Highlighting grains and dislocations using PHANTOM force feed- back device and tracking them to visualize the exact behavior of particular particle or dislocation can provide the researchers with a lot more information about the dynamics of the simulation.
Acknowledgements
The authors would like to take the opportunity to thank Dr. Ok Joon Kim in helping setup the Virtual Reality Devices for the demonstrations in the VRCIM Lab at WSU and Dr. Jagan Padbidri for sharing his expertise in contact mechanics.
References
- Li, H., Daugherty, T. and Biocca, F. (2001) Characteristics of Virtual Experience in Electronic Commerce: A Protocol Analysis. Journal of Interactive Marketing, 18, 13-30. http://dx.doi.org/10.1002/dir.1013
- Wexelblat, A. (1993) Virtual Reality Application and Exploration. Academic Press Professional, Boston.
- Klein, L.R. (2003) Creating Virtual Product Experiences: The Role of Telepresence. Journal of Interactive Marketing, 7, 41-55. http://dx.doi.org/10.1002/dir.10046
- Steuer, J. (1992) Defining Virtual Reality: Dimensions Determining Telepresence. Journal of Communication, 42, 73-93. http://dx.doi.org/10.1111/j.1460-2466.1992.tb00812.x
- Reeves, B. and Nass, C. (1996) The Media Equation: How People Treat Computers, Televisions, and New Media Like Real People and Places. Cambridge University Press, Cambridge.
- Biocca, F. (1997) The Cyborg’s Dilemma: Progressive Embodiment in Virtual Environments. Journal of Computer Me- diated-Communication, 3, 0-0.
- Li, H., Daugherty, T. and Biocca, F. (2003) The Role of Virtual Experience in Consumer Learning. Journal of Con- sumer Psychology, 13, 395-408. http://dx.doi.org/10.1207/S15327663JCP1304_07
- Suh, K.S. and Lee, Y.E. (2005) The Effects of Virtual Reality on Consumer Learning: An Empirical Investigation. Management Information Systems Quarterly, 29, 673-697.
- Jayaram, U. and Repp, R. (2002) Integrated Real-Time Calibration of Electromagnetic Tracking of User Motions for Engineering Applications in Virtual Environments. Journal of Mechanical Design, 124, 623-632. http://dx.doi.org/10.1115/1.1517562
- Jayaram, U., Jayaram, S., Shaikh, I., Kim, Y. and Palmer, C. (2006) Introducing Quantitative Analysis Methods into Virtual Environments for Real-Time and Continuous Ergonomic Evaluations. Computers in Industry, 57, 283-296. http://dx.doi.org/10.1016/j.compind.2005.12.005
- Panigrahi, S.R. (2009) Immersive 3D Visualization of Grain Structures and Dislocations in Materials. Masters’ Thesis, Washington State University, Washington DC.
- Johnson, K.L. (1987) Contact Mechanics. Cambridge University Press, Cambridge.
- Mueth, D.M., Jaeger, H.M. and Nagel, S.R. (1997) Force Distribution in a Granular Medium. Physical Review Letters, 57, 3164.
- Blair, D.L., Mueggenburg, N.W., Marshall, A.H., Jaeger, H.M. and Nagel, S.R. (2001) Force Distributions in Three- Dimensional Granular Assemblies: Effects of Packing Order and Interparticle Friction. Physical Review E, 63, Article ID: 041304. http://dx.doi.org/10.1103/PhysRevE.63.041304
- Mesarovic, S.D. and Fleck, N.A. (2000) Friction-Less Indentation of Dissimilar Elastic-Plastic Spheres. International Journal of Solids and Structures, 37, 7071-7091. http://dx.doi.org/10.1016/S0020-7683(99)00328-5
- Mesarovic, S.D. and Johnson, K.L. (2000) Adhesive Contact of Elastic-Plastic Spheres. Journal of the Mechanics and Physics of Solids, 48, 2009-2033. http://dx.doi.org/10.1016/S0022-5096(00)00004-1
- Mesarovic, S.D. and Padbidri, J. (2005) Minimal Kinematic Boundary Conditions for Simulations of Disordered Mi- crostructures. Philosophical Magazine, 85, 65-78. http://dx.doi.org/10.1080/14786430412331313321
- Mesarovic, S.D. (2005) Energy, Configurational Forces and Characteristic Lengths Associated with the Continuum Description of Geometrically Necessary Dislocations. International Journal of Plasticity, 21, 1855-1889. http://dx.doi.org/10.1016/j.ijplas.2004.09.002
- Radhakrishnan, H. and Mesarovic, S.D. (2009) Adhesive Contact of Elastic Spheres Revisited: Numerical Models and Scaling. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 465, 2231-2249.
- Zaeem, M.A., Kadiri, H.E., Mesarovic, S.D., Horstemeyer, M.F. and Wang, P.T. (2011) Effect of the Compositional Strain on the Diffusive Interface Thickness and on the Phase Transformation in a Phase-Field Model for Binary Alloys. Journal of Phase Equilibria and Diffusion, 32, 302-308. http://dx.doi.org/10.1007/s11669-011-9905-y
- Padbidri, J. and Mesarovic, S.D. (2011) Acceleration of DEM Algorithm for Quasistatic Processes. International Journal for Numerical Methods in Engineering, 86, 816-828. http://dx.doi.org/10.1002/nme.3076
- Cleary, P.W. and Sawley, M.L. (1999) Three Dimensional Modeling of Industrial Granular Flows. 2nd International Con- ference on CFD in the Minerals and Process Industries, Melbourne, 6-8 December 1999, 95-100.
- Cundall, P.A. (1971) A Computer Model for Simulating Progressive Large Scale Movements in Blocky Rock Systems. Proceedings of the Symposium of the International Society for Rock Mechanics, Society for Rock Mechanics (ISRM), France, II-8.
- Kuhn, M.R. and Bagi, K. (2004) Contact Rolling and Deformation in Granular Media. International Journal of Solids and Structures, 41, 5793-5820. http://dx.doi.org/10.1016/j.ijsolstr.2004.05.066
- Schall, P., Cohen, I., Weitz, D.A. and Spaepen, F. (2004) Visualization of Dislocation Dynamics in Colloidal Crystals. Science, 305, 1944-1948. http://dx.doi.org/10.1126/science.1102186
- Patriarca, M., Kuronen, A. and Kaski, K. (2002) Nucleation and Dynamics of Dislocations in Mismatched Hetero- Structures. Proceedings of Materials Research Society Symposium, 696, 125-130.
- Ohashi, T.L. (1999) Evaluation and Visualization of Geometrically Necessary Dislocations in Metal Microstructures by Means of Continuum Mechanics Analysis. Journal De Physique, 9, 279-284.
- Zbib, H.M., Rhee, M. and Hirth, J.P. (1998) On Plastic Deformation and the Dynamics of 3D Dislocations. Interna- tional Journal of Mechanical Sciences, 40, 113-127. http://dx.doi.org/10.1016/S0020-7403(97)00043-X
- Zbib, H.M. and Diaz de la Rubia, T. (2002) A Multiscale Model of Plasticity. International Journal of Plasticity, 18, 1133-1163. http://dx.doi.org/10.1016/S0749-6419(01)00044-4
- Zbib, H.M., Overman, C.T., Akasheh, F. and Bahr, D. (2011) Analysis of Plastic Deformation in Nanoscale Metallic Multilayers with Coherent and Incoherent Interfaces. International Journal of Plasticity, 27, 1618-1639. http://dx.doi.org/10.1016/j.ijplas.2011.03.006
- Alankar, A., Field, D.P. and Zbib, H.M. (2012) Explicit Incorporation of Cross-Slip in a Dislocation Density-Based Crystal Plasticity Model. Philosophical Magazine, 92, 3084-3100. http://dx.doi.org/10.1080/14786435.2012.685964
- Alankar, A., Mastoracos, I.N., Field, D.P. and Zbib, H.M. (2012) Determination of Dislocation Interaction Strengths Using Discrete Dislocation Dynamics of Curved Dislocations. Journal of Engineering Materials and Technology, 134, Article ID: 021018. http://dx.doi.org/10.1115/1.4005917
- http://www.cmm.wsu.edu/
- http://tetgen.berlios.de/
- Mills, S. and Noyes, J. (1999) Virtual Reality: An Overview of User-Related Design Issues: Revised Paper for Special Issue on Virtual Reality: User Issues in Interacting with Computers, May 1998. Interacting with Computers, 11, 375- 386. http://dx.doi.org/10.1016/S0953-5438(98)00057-5
- Pimentel, K. and Teixeira, K. (1994) Virtual Reality: Through the New Looking Glass. 2nd Edition, McGraw-Hill, New York.
- http://www.vrcim.wsu.edu/
- Appendix
- The following are sample input data from the data files used in rendering the grains, Delaunay networks, and the dislocations using OpenGL.
- In Table 1, the particle index is the indentifying index of a particular grain; X, Y, Z are the position vector of the particle; R is the radius of the particle; θx, θy, θz are the orientation vector of the particle; Vx, Vy, Vz are the velocity vector of the particle; ωx, ωy, ωz are the angular velocity vector of the particle; ax, ay, az are the accele- ration vector of the particle; and αx, αy, αz are the angular acceleration vector of the particle.
- Tetrahedral data is obtained by performing the Delaunay tetrahedralization on the set of particles with their centers assumed as points. The computation is performed by free software available called “tetgen”. The input is a file, which contains the coordinates of the points. The output is a list of tetrahedron and the vertices that form them, as an output file as shown in Table 2.
- This implies that the tetrahedron number 19 (from the above sample input data table) is formed by the points corresponding to the grain numbers or indices 15, 234, 6 and 78 of the input data file.
- To render a dislocation line, the location is represented by a point (X, Y, Z) and a vector (Lx, Ly, Lz). The “Line Index” is used to represent the dislocation lines lying in different slip planes. A sample data is provided in Table 3. In our OpenGL rendering we use this index as a color index to distinguish between different dislocations ly- ing in different slip planes.
Table 1. Sample input data of grain assembly.
Table 2. Sample input data for Delaunay tetrahedrons.
Table 3. Sample input data for crystal dislocations.










