Modeling and Numerical Simulation of Material Science
Vol.4 No.2(2014), Article ID:44356,17 pages DOI:10.4236/mnsms.2014.42008
Comparison of Functionals for Metal Hexaboride Band Structure Calculations
Jose A. Alarco1,2, Peter C. Talbot1,2, Ian D. R. Mackinnon1
1Institute for Future Environments, Queensland University of Technology, Gardens Point Campus, Brisbane, Australia
2Science and Engineering Faculty, Queensland University of Technology, Gardens Point Campus, Brisbane, Australia
Email: jose.alarco@qut.edu.au
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 December 2013; revised 20 January 2014; accepted 27 January 2014
Abstract
Density functional calculations of the electronic band structure for superconducting and semiconducting metal hexaborides are compared using a consistent suite of assumptions and with emphasis on the physical implications of computed models. Spin polarization enhances mathematical accuracy of the functional approximations and adds significant physical meaning to model interpretation. For YB6 and LaB6, differences in alpha and beta projections occur near the Fermi energy. These differences are pronounced for superconducting hexaborides but do not occur for other metal hexaborides.
Keywords
Hexaborides; Density Functional Theory; Band Structure; Spin Polarization; Superconductivity

1. Introduction
The flexibility of the boron framework in metal hexaborides accommodates a wide range of metal atoms or cation charges that results in a diversity of electronic and magnetic properties [1] [2] . We have previously evaluated properties of the hexaboride framework using precise experimental data and density functional theory [3] and recognized that, in general, property trends are defined by bond length adjustments within and between framework atoms.
The metal hexaborides offer an ideal structural system for comparison of computational models with physical properties as well as for validation of theories on bonding. The system is of relatively simple symmetry—cubic with space group Pm m—and contains only two elements. This simplicity of composition and structure affords facile computation and interpretation of model outcomes. Depending on the metal ion within the structure, boron accommodates both covalent and ionic bonding to varying degree within and between the B6 octahedra that comprise the structural framework. Boron-boron and metal-boron bonds clearly influence the electronic properties extant in the hexaboride suite [3] and are explored in more detail in this work.
m—and contains only two elements. This simplicity of composition and structure affords facile computation and interpretation of model outcomes. Depending on the metal ion within the structure, boron accommodates both covalent and ionic bonding to varying degree within and between the B6 octahedra that comprise the structural framework. Boron-boron and metal-boron bonds clearly influence the electronic properties extant in the hexaboride suite [3] and are explored in more detail in this work.
Electronic properties are generally controlled by the behavior of electrons within a small energy range (~kBT, where kB is Boltzmann’s constant and T is the absolute temperature) around the Fermi energy [4] -[6] . Electronic band structure calculations for the electrons in the normal state of LaB6 and YB6, two of the metal hexaborides that display superconductivity, attribute predominant d metal character to the electrons at the Fermi level, with large contributions from boron 2p character [7] -[9] . In this paper, we use density functional theory (DFT) to model electron behaviors at the Fermi energy, including all interactions in which the electrons participate, and the characteristics of bonding electrons in metal hexaborides.
Boron bonding in metal hexaborides is complex and integral to a boron framework that is highly responsive to structural variations [3] . This work evaluates the factors that control electron dynamics at the Fermi energy in metal hexaborides, particularly in regions of interest identified in an earlier paper [3] . Model calculations are subjected to a wide range of initial setup conditions, which include more accurate functional approximations to account for exchange interactions and correlations, consideration of the material system as metal or non-metal and evaluation of spin polarization.
2. Calculation Methods
We have performed an extensive comparison of DFT calculations using the CASTEP module [10] of Materials Studio 6.1, with various functionals, applied to a selection of metal hexaborides. Starting with the simplest local density approximation (LDA), a range of functionals with particular intrinsic errors are tested including the generalized gradient approximation (GGA), Hartree-Fock approximation (HF-LDA), the exchange-correlation function by Ceperley and Alder (CP) [11] parameterized by Perdew and Zunger (PZ) [12] , screened Hartree-Fock (sX-LDA), the hybrid functional by Becker, Lee, Yang and Parr (B3LYP) and the screened hybrid functional by Heyd, Scuseria and Ernzerhof (HSE06) [13] [14] . All calculations use an ultrafine grid choice and plane-wave (PW) basis, linear response functions, norm-conserving pseudo potentials, Pulay density mixing schemes (when the method allowed, otherwise the program choice is All Bands/EDFT) and fine interpolation methods. The PW basis set cut-off is typically >290 eV and the energy cut off is 10 eV. For display of results, the instrument broadening default value of 0.050 eV is retained, as this value is technique and/or instrument specific.
Although the oxidation state of the atom can be specified during parameter input for the crystal structure, results from test calculations that assumed different oxidation states for the atoms did not differ from those for zero oxidation state. Given this result, subsequent calculations reported here assume zero oxidation state for constituent atoms.
For calculations that utilized full geometry optimization, an estimate of the physical accuracy of these firstprinciples calculations is obtained. These optimizations use as input values the refined unit cell parameters from X-ray or neutron diffraction of well determined hexaboride single crystal studies [3] . For calculations, which do not include optimization of the unit cell in the geometry optimization, lattice parameters determined from refinements of X-ray and/or neutron diffraction data are used [3] , but fractional atomic coordinates are optimized in order to compare approximations for the various electronic band structure calculations. For cases where geometry optimization is not carried out, the band structure is calculated in the energy task of the setup, using the full set of structural parameters refined from X-ray and/or neutron diffraction data [3] .
Possible effects of spin polarization on the band structure are calculated using the CASTEP program. For this software, spin polarization models require treating the compound as a non-metal. The CASTEP program confers explicit constraints on electronic models depending on the choice of “metal” or “non-metal” configuration. The “metal” option in CASTEP [10] corresponds to a tighter program setting (that is usually associated with the modeling of metals, hence the name “metal”). However, this term as used in the program does not of itself mean that the subject material is a metal [15] .
In essence, the number of occupied bands for insulators is calculated as half the total number of valence electrons. However, this approach is not suitable for metals [13] . For metallic systems, partial occupancies are introduced to eliminate discontinuous changes in total energy that are created when an energy band crosses a Fermi level during self consistent field (SCF) minimization [13] . This change in orbital occupancy from fixed to un-fixed automatically introduces smearing of the energy levels as described in detail below. Spin polarization calculations focus on YB6 and CaB6, since these compounds represent an electron-doped and a complete orbital configuration, respectively.
Most calculations are completed using Materials Studio 6.1 via the Microsoft Windows mode of a 12 core Mac Pro Xeon 64bit workstation. This workstation operates with an Intel chip and mimics up to 24 cores. When memory requirements exceed the capacity of this computer, calculations are undertaken via the High Performance Computing (HPC) facility at QUT using multiples of 16 cores. The optimum choice for calculations on the HPC facility is 64 cores.
3. Bonding in Metal Hexaborides
The literature shows a range of approaches to analyze and describe boron bonds in metal hexaborides. Some approaches allow easier visualization of electron distribution, for example, while others facilitate model calculations. These broad approaches are briefly reviewed below.
3.1. Molecular Orbital Models
Molecular orbital (MO) models that build the structure as a linear combination of boron atomic orbitals of valence electrons (not including core electrons) using a tight-binding approximation occurs in the early work of Longuet-Higgins and de V. Roberts [16] . A similar tight-binding approach with detailed group theoretical analysis of MO in metal hexaborides is given by Yamazaki [17] . A slightly modified version (normally referred to as the Valence Bond approach) where the inter-octahedral bonds are considered simple localized bonds using sp hybrids from each boron atom, can be found in the book by Urch [18] . Although these models do not embrace the conventional paradigm with ligands coordinated to a metal cation, the lack of a cation implies that the interactions between ligands hold the B6 cluster together [18] . Both MO models lead to a suite of 18 orbitals, six with primary sp hybrid character (a1g, t1u and eg) and 12 with p hybrid character (t1g, t2g, t1u, t2u) involving the 6 borons in an octahedral cluster. Of these 18 orbitals, seven (a1g, t1u and t2g, where t1u and t2g have p hybrid character) have bonding character. This configuration requires 14 electrons to hold the B6 cluster together (two of which would be donated by the metal atom), and 11 orbitals (eg, t1u, t2u and t1g) have antibonding character [18] .
3.2. Cluster Approach to B6 Octahedra
While largely pertaining to a MO approach, cluster properties of the boron octahedra [19] -[22] can provide further insight. These structures can be viewed as a metal boron cluster where the stability of cluster assembly [23] is determined by the nature of boron bonding. The quantum states in metal clusters adopt a super shell structure with associated orbitals that mimic the characteristics of atoms and give rise to the concept of a super atom [24] [25] . The quantum confinement in nearly spherically symmetric clusters results in the electronic shell sequence:

originally introduced through the concept of a jellium spherical potential [19] [25] , that is attractive, constant within a given radius and zero outside that radius [26] . Electrons contributed by the valence orbitals of the atoms in the cluster fill nl orbitals in keeping with the Pauli exclusion principle. However, due to the nature of charge distribution in the clusters, the ordering of these nl levels is different to conventional configurations. Although these electronic shells are introduced via the jellium model, the existence of electronic shells in fermionic systems is known for a far wider range of potentials [25] .
Furthermore, when interacting electrons are considered and the octahedral geometry of the cluster is included, a partial breaking of the 1d degeneracy is expected [27] . This loss of degeneracy results in cluster orbitals with the symmetry sequence: a1g, t1u, t2g and eg, which matches the MO configuration for all the bonding orbitals up to the first antibonding orbital [16] [18] . The t2g and eg orbitals of the boron cluster indicate that electrons at the highest occupied molecular orbital (HOMO) and at the lowest unoccupied molecular orbital (LUMO) resemble “d-like” symmetry behavior. Thus, clusters may open detectable gaps via splitting of the shells due to the arrangement of ionic cores similar to crystal field splitting of atomic d states through the electric fields of surrounding ions in solids [24] [27] . As such, Hund’s rules favor high spin states in open shell systems stabilized by exchange coupling, and similarly, orbital occupation is expected to be determined by a trade-off between Hund’s rules and possible Jahn-Teller effects.
3.3. United Atom Configuration
A complete understanding of MO requires recognition of the atomic orbitals into which they revert at large inter-nuclear distances, and the configuration when the inter-nuclear distance is reduced to zero and the participating nuclei coalesce [22] [28] . The understanding of molecular structure derived from such correlation diagrams parallels that of atomic structure afforded by the periodic table [28] .
In the case of metal hexaborides, two united atom conditions can be envisaged: 1) as the atoms move away from the boron octahedral clusters at the vertex and meet at the middle points of the cube sides; and 2) as the atoms coalesce at the cube vertex. The first condition results in a dodecahedral coordination of coalesced B2 clusters, while the second results in a cubic coordination of coalesced B6 clusters. In this latter case, the B6 cluster is equivalent to the super atom approach described above. Note that for metal hexaborides, if the metal is to have d character, the crystal or ligand field splitting goes in the same direction for dodecahedral and for cubic coordinations (see Figure 2.7 in reference [29] ). Therefore, the effects of ligands on the metal in a metal hexaboride can be considered as a crystal or ligand field condition intermediate between these two united atom conditions.
4. Earlier Band Structure Calculations
As mentioned above, both Longuet-Higgins and de V. Roberts [16] and Yamazaki [17] , use tight binding approximations to describe metal hexaboride band structures. Later, Perkins et al. [30] attribute the difference between their results and those of Yamazaki [17] to inclusion of overlap between Bloch functions of the same symmetry [30] . Furthermore, Perkins et al. [30] found that in three metal hexaboride solids (i.e. Ca, Sr and Ba), the metal atoms transfer 0.9, 1.0 and 0.0 electrons to the B6 cage in each unit cell, respectively. Thus, they argue that there is no absolute requirement for each B6 cage to acquire two electrons for stability in the solid-state [30] . According to Perkins et al. [30] , in all hexaboride metallic systems, the metal s states partake in bonding that broadens the lowest valence band along the Λ, Σ and Δ directions. These directions are equivalent to GR, GM and GX, respectively, in CASTEP calculations [3] . However, Perkins et al. [30] hold that no significant s orbital contribution is found at the Fermi surface.
In later work, Hasegawa and Yanase [31] use a non-relativistic, symmetrized augmented plane wave (APW) method to calculate the band structure of LaB6, constructing a one electron potential on the basis of Slater’s Xα method. An interesting point mentioned by Hasegawa and Yanase [31] , and also attributed to Longuet-Higgins and de V. Roberts [16] , is that the six s states of the B atoms in an octahedron, as well as the six p states of these B atoms, form together d-like orbitals retaining some of the symmetry about the B6 octahedral centre. These d-like orbitals and the La d state have nearly equal energies in LaB6, and therefore, strong hybridization occurs. Similarly, Walch et al. [32] examine the predictions of the Hartree-Fock-Slater (HFS) model for the occupied levels and low-energy excitations of LaB6, adopting the simplest, one-electron direct-transition interpretation of the excitation spectrum. Two possible neutral atom configurations for La, i.e. La: 5d16s2 and La: 5d26s1 are compared. This work re-emphasizes the importance of the La-B bond, in contrast to earlier work that attributes a predominant, or an unduly large, role for electronic conduction to the La-La metal bond.
For CaB6, Hasewaga and Yanase [33] use a self-consistent augmented plane wave (APW) method with the local-spin density approximation (LSDA), taking into account relativistic effects in a fashion that eliminates spin-orbit interaction terms from the Hamiltonian. They compare muffin-tin and non-muffin tin corrections and show that these corrections can have a large effect on the value of the semiconducting gap. They determine a gap of 0.3 eV for CaB6, and suggest this is in good agreement with an experimental result of 0.4 eV from Johnson and Daane [33] .
A renewed interest in CaB6 is triggered by experimental observation of ferromagnetism at high temperature in La-doped forms of CaB6 [34] -[40] . Many studies on CaB6 explore whether this hexaboride is a semiconductor or a semimetal [35] [37] [41] [42] .
A wide array of experimental techniques is utilized to determine the band gap of a material. In addition to temperature dependence of resistivity by Johnson and Daane [33] , angle resolved photoemission spectroscopy (ARPES) [35] [36] , resonant inelastic X-ray scattering (RIXS) [35] , electron energy loss spectroscopy (EELS) and transport [38] , optical absorption and tunneling conductance [43] are reported for metal hexaborides. Table 1 lists the experimental and theoretical results in the literature for determination of the CaB6 band gap.
To date, few theoretical models for this simple CaB6 structure have been systematically compared with each other or with similar parameter attributes. Thus, it is difficult to evaluate the actual value for the CaB6 band gap, particularly with the wide range of outcomes listed in Table 1. The estimated band gap values show significant variations whether determined experimentally or through DFT calculations.
A systematic comparison of CASTEP models including initial conditions and choice of functional parameters allows identification of potential, non-obvious sources of disparity in theoretical results and effective comparison with experimental data.
A wide range of metal hexaboride band structure calculations within the framework of DFT use the local density approximation (LDA) and the generalized gradient approximation (GGA) [3] [7] [9] [48] [49] . The LDA is exact in the uniform electron density limit and the GGA includes information on the spatial variations in electron density, using functions which are only valid for slowly varying densities [50] [51] . These DFT calculations show similar results on the shapes of the bands and emphasize the GM join as a region in reciprocal space near the Fermi surface of particular interest [3] [9] .
The accuracy of the DFT calculations encompasses both a mathematical and a physical context [50] [51] . Views on which functional provides the most accurate results appear to be material system and property specific, evolving with time and undergoing revision on a regular basis [15] [50] -[61] . The transition point where the prescribed accuracy of the functional refers to a molecular orbital or to an extended solid-state material is not always clear.
Recently, Lejaeghere et al. [62] have reviewed the intrinsic and numerical errors for DFT predictions. This statistically based evaluation provides guidelines for the assignment of percentage errors and benchmark comparison of calculated and experimental results for many elements of the periodic table. While this work focuses on elemental crystalline solids, verification of the methodology on multicomponent solids suggests that intrinsic errors for prediction of materials properties are low [62] .
5. DFT Model Results
The physical properties (e.g. superconductivity) for which there are unequivocal experimental data on metal hexaborides occur at low temperatures (<10 K). The overarching effect of temperature, particularly with theoretical models based on room temperature structural data such as lattice parameters, places limitations but also reality checks, on the viability of specific models. In this work, we compare model calculations on the basis of
Table 1. Experimental and theoretical estimates of CaB6 band gaps.
**LDA shows that the valence and conduction bands touch at the X point. However, the instrumental resolution of 1.6 - 1.8 eV in this study may not resolve a gap around 1 eV.
structural parameters determined from room temperature refinements [3] . Experimental data [63] [64] show that structural parameters of hexaborides adjust at low temperatures, and in limited cases [65] , can show non-linear step changes in cell dimension at low temperatures. Nevertheless, for the purposes of these model evaluations, comparisons are performed using structural parameters determined at room temperature as this is a reliable reference point.
As noted earlier, the viability and fidelity of specific computational models is evaluated through comparison with well defined, precise experimental data on structural parameters [3] for metal hexaborides. The models used, and the functionals that comprise each model are listed in Tables 2 and 3. The relative fidelity of calculated parameters compared with experimental values (shown as the parameter, δB or δa) is shown in Tables 2 and 3.
Table 2 lists ten different models utilizing 34 different combinations of functional for the YB6 structure. Table 2 shows that few combinations of DFT models calculate a cell dimension for YB6 equivalent to the experimentally determined value. Only the LDA-CA-PZ combination and the B3LYP model generate a cell dimension similar to the experimental value primarily because the cell dimension is not optimized nor refined during the calculation.
For YB6, within the LDA-CA-PZ set of comparisons, the non-metal, spin polarized option produces structural parameters closest to experimental data with full geometry optimization. If the lattice parameter is not optimized, a similar outcome occurs with selection of a metal configuration and unpolarized spins. Full geometry optimization in the GGA-PBE approximation produces similar outcomes when the YB6 system is modeled as a non-metal. Models using a non-metal, spin polarized selection provides calculated structural parameters similar to experimentally-determined values.
In all other cases, except for the LDA + U GGA-PBE model without metal configuration, the calculated cell dimension is underestimated compared with the experimental value. Calculation of bond length (B-Bout) is consistent with experimental values where the parameter is not refined or optimised and, in general, is overestimated for LDA-CA-PZ configurations of DFT models.
In general, not selecting the “metal” option provides closer approximations to experimental values. Calculations with occupancy fixed, not unexpectedly, provide values closer to the experimentally determined cell dimensions. If the calculation includes selection of the “metal” option, the capacity to calculate a band structure with fixed occupancy is not allowed.
Table 3 lists five different models utilizing 31 different combinations of functional for CaB6. For CaB6, optimization of the unit cell for the LDA-CA-PZ approximation is sufficient to cause overlap between the conduction and valence bands and to destroy any indication of a band gap. This outcome is due to a reduction in both the lattice parameter and the B-Bout distance relative to input values. If the input values are not optimized, a small gap of 0.016 eV results. Optimizing the B-Bout distance without changing the lattice parameter produces a slight increase in the B-Bout distance relative to the input value, and results in a slightly larger gap of 0.048 eV.
Using the GGA-PBE approximation, the resulting lattice parameter and the B-Bout distance for CaB6 do not deviate significantly from the input values. In this case, the band gap is comparable to the largest values of the LDA-CA-PZ approximation (0.039 - 0.048 eV). The use of these functions suggests a modest correlation between the B-Bout distance and energy gap as noted by Schmitt et al. [66] . Table 3 lists other calculations with band gaps ranging from 0.077 eV to 0.149 eV and between 0.196 eV and 0.394 eV. A significant correlation between the magnitude of the energy gap and B-Bout value is observed in these calculations.
For CaB6, Table 3 shows that choice of a spin polarized calculation is not significant for band gap estimation compared with the spin unpolarized calculation with less accurate functionals (e.g., the LDA-CA-PZ, GGA-PBE and sX-LDA-CA-PZ choices in Table 3). With a more accurate functional, such as the HSE06 [13] [14] , a difference of ~0.070 eV occurs between the polarized and non-polarized calculations. This suggests that spin polarization effects are of the same order of energy as the energy of characteristic phonons of metal hexaborides [67] [68] . Hence, coupling between electron spin polarization and phonons in this system is probable.
A lack of, or limited, spin polarization dependence largely originates from the fact that CaB6 contains an even number of electrons. The computational protocol for CASTEP calculations is that the number of orbitals is determined as the number of electrons divided by two, with sequential pairs of electrons within available orbitals [13] , so that no unpaired electron remains in a system with an even number of electrons.
The above computational protocol is confirmed by similar calculations using YB6 super cells (data not shown). With an even number of super cells, such as 2 × 2 × 2 or 4 × 4 × 4, spin polarization dependence is lost, while
Table 2. Model conditions used for electronic band structure calculations for YB6 (input experimental parameters a = 4.1000 Å and B-Bout = 1.6300 Å [3] ).
Table 3. Model conditions used for band structure calculations for CaB6 (input lattice parameter: a = 4.1514 Å and B-Bout = 1.6760 Å [3] ).
spin polarization dependence is apparent with an odd number of super cells such as 3 × 3 × 3. Other evaluations of spin polarized super cell calculations (e.g. via sX-LDA and HSE06), particularly with an ultra-fine grid, did not converge.
5.1. Metals or Insulators—Electron Smearing
CASTEP calculations differentiate between metals and insulators on the basis of occupied bands at different k-points in the Brillouin zone. For insulators, the number of occupied bands is calculated as one half the total number of valence electrons. As noted above, these options for CASTEP calculations introduce the concept of electron energy smearing which is computationally possible between 0.01 eV and 10 eV. These energy values correspond to temperatures of ~116˚K and ~116,000˚K, respectively (using Energy ≈ kBT, where kB is Boltzmann’s constant). In terms of temperature equivalence, these energies are excessively large for phenomena that may be dominated by low temperature interactions and couplings active at a few degrees Kelvin. For instance, the superconducting transition temperature for YB6 is 7.1 K [69] [70] .
The smearing default values in CASTEP are 0.1 eV and 0.2 eV, respectively, for orbital occupancy and for display of the density of states (DOS). All default values in CASTEP are a reasonable average choice for common modeling conditions, although caution is advised with respect to the selection of smearing values [13] . However, comparable values around 0.1 eV to 0.2 eV are the preferred choice when the modeling intent is to remove potential local mathematical instabilities at the Fermi energy. Unfortunately, it is not always apparent that such choices may force the modeled system to undergo an unrealistic, non-physical, equivalent temperature condition for the property of interest.
For example, in a system close to a Mott metal-insulator transition, small energy pseudo gaps of tens of meV (or even smaller gaps), may play an important role [71] . Thus, smearing of orbitals with a 0.1 eV or 0.2 eV value may sacrifice, unnecessarily and detrimentally, important physical information about the system. Furthermore, all equivalent temperature effects from smearing are likely to introduce a non-directional random character, which may not always correspond to the limited and most intense phonon modes. These phonon modes will dominate system behavior at low temperatures. To minimize this issue, we have chosen a fine interpolation for the display of DOS.
Similar effects are evident for model calculations with the metal option selected in CASTEP calculations. Typically, the standard default value of 0.1 eV overrides spin polarized results in metal hexaboride systems with an odd number of electrons. This outcome indicates that the energy differences related to spin dependence are smaller than 0.1 eV. Recovery of spin polarization is apparent for the lower limit of smearing at 0.01 eV. However, as noted above, this value may be too high for physically meaningful temperature equivalence. If the “no metal” option is selected without fixed occupancy while using the SCF electronic minimizer setup, the outcome is similar to selection of a metal due to the introduction of electron energy smearing.
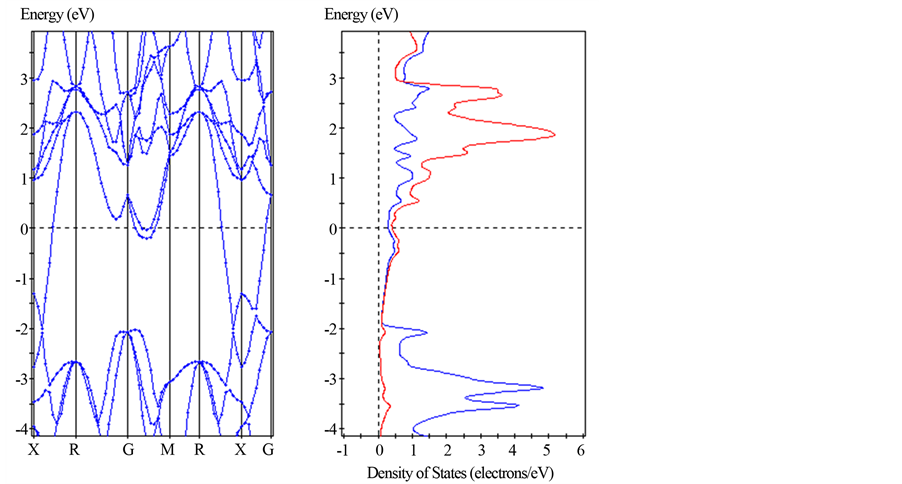
Figure 1 shows the effects on band structure calculations for YB6 with different model options chosen for “metal” or “no metal” and for choice of fixed occupancy. A shift of about 0.25 eV relative to the Fermi energy in all bands and DOS is clearly evident for these two model choices. The shift in band structure using the LDA-CA-PZ function illustrates the importance of appropriate model selection.
The recent review article by Lejaeghere et al. [62] emphasizes that, in general, comparison of DFT calculations with experimental results requires that the experimental results should refer to 0˚K and that measurements are corrected for zero-point vibration effects, which are not present in standard DFT calculations. Alternatively, DFT calculations should incorporate interactions and phenomena that appear and vary as temperature changes.
5.2. Spin Polarization
Calculation trends from this work on hexaborides indicate that inclusion of spin polarization produces more accurate lattice parameter and B-Bout values. When the spin polarized option is chosen for CASTEP calculations, different wave functions for different spins are used [13] . If a calculation without spin polarization is chosen, the same orbitals for alpha and beta spins are used. Thus, spin polarization effectively results in an increased number of parameters for the calculation, which may lead to a better mathematical approximation, and to a better quantum mechanical approximation provided assumptions about spins in the system reflect physical reality.
Spin-polarized CASTEP calculations are normally carried out with a variable magnetic moment [13] . How-
 (a)
(a) (b)
(b)
Figure 1. Calculated band structures for YB6 using the LDA-CA-PZ functional; assumes no geometrical optimization and no spin polarization with (a) “metal” option and (b) “nonmetal” option. Note that the energy bands adjacent to the Fermi surface along the GM join and the DOS are shifted by about 0.25 eV in (b) compared to (a).
ever, this procedure does not guarantee that the lowest energy state is determined as DFT solutions can converge to a variety of local minima related to metastable states. The most common solutions correspond to high spin and low spin states. The state generated by CASTEP calculations depends on the initial magnetic configuration, since the solution is likely to converge to the nearest local minimum rather than to a global minimum. Initial magnetic moments on atoms are treated correctly by CASTEP only when the density mixing (DM) scheme is used for electronic minimization [64] .
However, our comparison of the DM and the all bands (AB) schemes for electronic minimization revealed similar results for the spin polarized bands of YB6. When there is one unpaired electron in the unit cell, the risk of convergence to multiple local minima is reduced. This outcome may not occur if more than one electron is unpaired as may be for CaB6 if, for example, two electrons are assumed unpaired.
Figure 2 shows examples of YB6 band structure calculations that include spin polarization using the B3YLP functional. The band structures in Figure 3 for YB6 are calculated using the HSE06 functional. Both of these functionals are considered accurate choices [13] [14] [50] -[61] for quantum mechanical calculations. Figure 3(a) also compares the calculation for unpolarized spins with the HSE06 functional.
Although both functionals lead to somewhat different lattice parameters and B-Bout distances, the qualitative effects on the band structures adjacent to the Fermi energy are quite similar. The band splits at the RG and GM sections, and results in a strong alpha component close to the Fermi energy with another component moving to higher energies in sections adjacent to G. The same alpha band also develops sections along the R direction much closer to the Fermi energy.
Although the amounts of band splitting or the proximity to the Fermi energy along the R direction are not always identical, this phenomenon is qualitatively the same for many non-metal, spin polarized calculations with different functionals. This reproducibility of trends for the bands and DOS combined with optimized parameters close to the experimental input values suggest that spin polarization is a physical reality for YB6 at low temperatures. We expect that in a single electron approximation for YB6, the compound requires an amount of spin in order to participate in coupling for superconductivity and to produce perfect diamagnetic Meissner effects.
In order to extract additional physical information from this spin polarization dependence, we display various DOS components for YB6 and LaB6. Figures 4 and 5 show the p and d spin components and the alpha and beta components calculated for YB6 and LaB6, respectively. YB6 displays more pronounced differences adjacent to the Fermi energy than LaB6. These differences are indicative of a requirement for stronger coupling in YB6 compared to that in LaB6, likely relating to superconductivity, and the correspondingly higher Tc for YB6 compared to LaB6.
While there may be minor inadequacies with assumptions in DFT calculations, the accuracy of results is improved using spin polarization. When this increased accuracy of model calculation is combined with a physical interpretation of a magnetic contribution to the hexaboride structure, differentiation of YB6 and LaB6 properties is evident. In this case, we indicate that spin polarization may be crucial to the correct determination and interpretation of electronic band structure for superconducting (and other magnetic) materials, particularly at low temperatures.
6. Conclusions
The electronic band structures of metal hexaborides are calculated for a range of models using a variety of density functionals. This systematic evaluation of band structure calculations for metal hexaborides identifies factors that account for the disparity of previously reported theoretical values.

Figure 2. Calculated band structures for YB6 using the B3LYP functional; assumes “no metal” with geometrical optimization and spin polarization. Note that the spin polarized energy bands develop a strong alpha component adjacent to the Fermi surface along the RG and MR joins.

Figure 3. Calculated band structures and DOS using HSE06 function, assumes “no metal” with geometrical optimization with (a) no spin polarization and (b) spin polarization for YB6. Both calculations use the same structural input parameters. (c) Calculated band structures and DOS for LaB6 using the B3LYP function, assumes “no metal” with geometric optimization and spin polarization.
The mathematical procedure used to avoid discontinuities when an energy band crosses the Fermi energy during SCF minimization gives rise to flexible orbital occupation accompanied by smearing of energy levels in model calculations. Such smearing is equivalent to unrealistically high temperatures which may mask fine band and DOS detail related to physical phenomena at very low temperature (i.e. near 0˚K). For instance, effects related to coupling for low-temperature superconductivity or a Mott metal-insulator transition may not be detected for materials with gaps or pseudo gaps of a few meVs.
Consideration of spin polarization improves the numerical accuracy and the physical interpretation of associated phenomena. Calculated spin polarization effects for metal hexaborides are typically concentrated adjacent to the Fermi energy and thus, affect electronic properties. For YB6 and LaB6, unpolarized bands are split into (a) a large alpha component that approaches the Fermi energy in large regions of reciprocal space, and (b) another

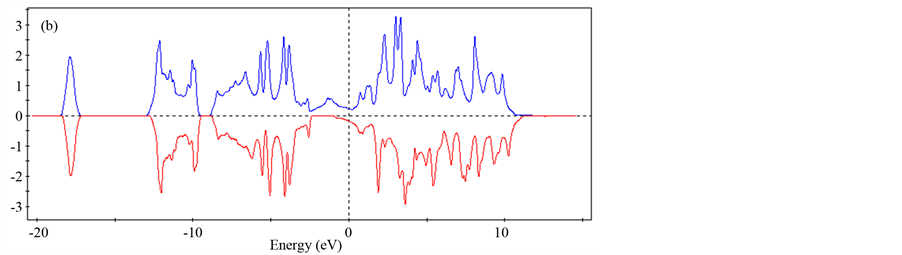
Figure 4. Partial DOS for YB6 using the HSE06 function, for “non-metal” with geometric optimization and spin polarization: (a) p (blue line) and d spin components, (b) alpha (blue line) and beta components. Note that the d spin projection is larger in magnitude than the p spin projection near the Fermi energy. The asymmetry in (b) around the Fermi energy is responsible for a net spin.
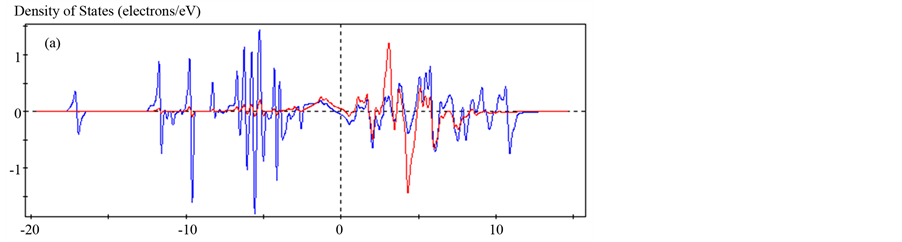
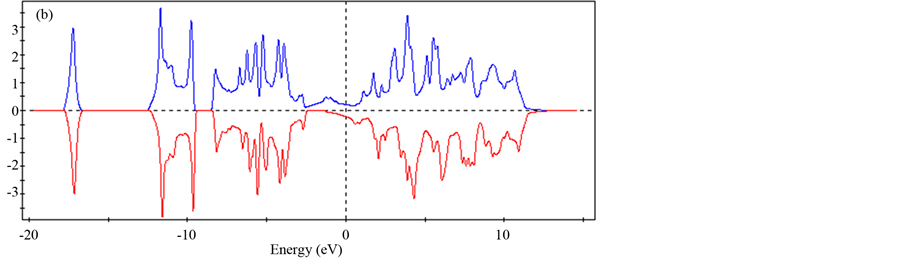
Figure 5. Partial DOS for LaB6 using the B3LYP function, assuming “nonmetal” with geometric optimization and spin polarization: (a) p (blue line) and d spin components, (b) alpha (blue line) and beta components. Note that the p spin and d projections are similar for LaB6 compared with data for YB6 shown in Figure 4.
alpha component that trends away from the Fermi energy particularly near the G section. Slight differences in alpha and beta projection in the DOS for YB6 and LaB6 may correlate to different superconducting transition temperatures.
Acknowledgements
Financial support from QUT is gratefully acknowledged. The authors are grateful to Ashley Wright and Mark Barry from the High Performance Computing (HPC) facilities at QUT for their assistance, as well as to Professor John Barry from the Institute for Future Environments for fruitful discussions.
References
- Samuely, P., Reiffers, M., Flachbart, K., Akimenko, A.I., Yanson, I.K., Ponomarenko, N.M. and Paderno, Y.B. (1988) Point-Contact Spectroscopy of the Electron-Phonon Interaction in Single-Crystal LaB6. Journal of Low Temperature Physics, 71, 49-61.
- Werheit, H., Filipov, V., Shitsevalova, N., Armbrüster, M. and Schwarz, U. (2012) Isotopic Phonon Effects in LaB6- LaB6 Do Not Possess Cubic Symmetry and Show a Non-Random Isotope Distribution. Journal of Physics: Condensed Matter, 24, 385405-1-14. http://dx.doi.org/10.1007/BF00115040
- Mackinnon, I.D.R., Alarco, J.A. and Talbot, P.C. (2013) Metal Hexaborides with Sc, Ti or Mn. MNSMS, 3, 158-169. http://dx.doi.org/10.4236/mnsms.2013.34023
- Ziman, J.M. (1972) Principles of the Theory of Solids. 2nd Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139644075
- Myers, H.P. (2002) Introductory Solid State Physics. 2nd Edition, CRC Press, Boca Raton.
- Springford, M., Ed. (1980) Electrons at the Fermi Surface. Cambridge University Press, Cambridge.
- Grechnev, G.E., Baranovskiy, A.E., Fil, V.D., Ignatova, T.V., Shitsevalova, N.Yu., Filippov, V.B. and Eriksson, O. (2008) Electronic Structure and Bulk Properties of MB6 and MB12 Borides. Low Temperature Physics, 34, 921-929. http://dx.doi.org/10.1063/1.3009588
- Schell, G., Winter, H., Rietschel, H. and Gompf, F. (1982) Electronic Structure and Superconductivity in Metal Hexaborides. Physical Review B, 25, 1589-1599. http://dx.doi.org/10.1103/PhysRevB.25.1589
- Hossain, F.M., Riley, D.P. and Murch, G.E. (2005) Ab initio Calculations of the Electronic Structure and Bonding Characteristics of LaB6. Physical Review B, 72, 235101-1-235101-5. http://dx.doi.org/10.1103/PhysRevB.72.235101
- Clark, S.J., Segall, M.D., Pickard, C.J., Hasnip, P.J., Probert, M.J., Refson, K. and Payne, M.C. (2005) First Principles Methods Using CASTEP. Zeitschrift fur Kristall, 220, 567-570. http://dx.doi.org/10.1524/zkri.220.5.567.65075
- Ceperley, D.M. and Alder, B.J. (1980) Ground State of the Electron Gas by a Stochastic Method. Physical Review Letters, 45, 566-569. http://dx.doi.org/10.1103/PhysRevLett.45.566
- Perdew, J.P. and Zunger, A. (1981) Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems. Physical Review B, 23, 5048-5079. http://dx.doi.org/10.1103/PhysRevB.23.5048
- Materials Studio CASTEP Online Help, CASTEP Occupancy Option Dialog. http://www.tcm.phy.cam.ac.uk/castep/documentation/WebHelp/CASTEP.htm
- Grimme, S. (2006) Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. The Journal of Chemical Physics, 124, 034108. http://dx.doi.org/10.1063/1.2148954
- Liang, J.-J. (2012) Accelrys, CASTEP Customer Support, Personal Communication.
- Longuet-Higgins, H.C. and Roberts, M.D.V. (1954) The Electronic Structure of the Borides MB6. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 224, 336-347. http://dx.doi.org/10.1098/rspa.1954.0162
- Yamazaki, M. (1957) Group Theoretical Treatment of the Energy Bands in Metal Borides MeB6. Journal of the Physical Society of Japan, 12, 1-6. http://dx.doi.org/10.1143/JPSJ.12.1
- Urch, D.S. (1970) Orbitals and Symmetry. Penguin Books Ltd., Harmondsworth, Middlesex
- Johnston, R.L. (2002) Atomic and Molecular Clusters. In: Betts, D.S., Ed., Masters Series in Physics and Astronomy, Taylor & Francis, London.
- Fox, M.A. and Wade, K. (2003) Evolving Patterns in Boron Cluster Chemistry. Pure and Applied Chemistry, 75, 1315- 1323. http://dx.doi.org/10.1351/pac200375091315
- Zubarev, D.Y. and Boldyrev, A.I. (2007) Comprehensive Analysis of Chemical Bonding in Boron Clusters. Journal of Computational Chemistry, 28, 251-268. http://dx.doi.org/10.1002/jcc.20518
- Hauser, A.W., Callegari, C. and Ernst, W.E. (2009) Level-Structure and Magnetic Properties from One-Electron Atoms to Clusters with Delocalized Electronic Orbitals: Shell Models for Alkali Trimers. In: Piecuch, P., et al., Eds., Advances in the Theory of Atomic and Molecular Systems—Dynamics, Spectroscopy, Clusters and Nanostructures, Springer, Berlin. http://dx.doi.org/10.1007/978-90-481-2985-0_10
- Khanna, S.N. and Jena, P. (1992) Assembling Crystals from Clusters. Physical Review Letters, 69, 1664-1667. http://dx.doi.org/10.1103/PhysRevLett.69.1664
- Medel, V.M., Reveles, J.U., Khanna, S.N., Chauhan, V., Sen, P. and Castleman, A.W. (2011) Hund’s Rule in Superatoms with Transition Metal Impurities. Proceedings of the National Academy of Sciences of the United States of America, 108, 10062-10066. http://dx.doi.org/10.1073/pnas.1100129108
- Castleman, A.W. and Khanna, S.N. (2009) Centennial Feature Article: Clusters, Superatoms, and Building Blocks of New Materials. The Journal of Physical Chemistry C, 113, 2664-2675. http://dx.doi.org/10.1021/jp806850h
- Ashman, C., Khanna, S.N. and Pederson, M.R. (2002) Electron Attachment and Dynamics of Alkali Atoms in Al13X (X = Li – Cs) Clusters. Physical Review B, 66, 193408. http://dx.doi.org/10.1103/PhysRevB.66.193408
- Weigend, F. and Ahlrichs, R. (2010) Quantum Chemical Treatments of Metal Clusters. Philosophical Transactions of the Royal Society A, 368, 1245-1263. http://dx.doi.org/10.1098/rsta.2009.0268
- Coulson, C.A. (1963) Valence. 2nd Edition, Oxford University Press, London.
- Burns, R.G. (1993) Mineralogical Applications of Crystal Field Theory. 2nd Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511524899
- Perkins, P.G., Armstrong, D.R. and Breeze, A. (1975) On the Electronic Structure of Some Metal Hexaborides. Journal of Physics C: Solid State Physics, 8, 3558-3570. http://dx.doi.org/10.1088/0022-3719/8/21/026
- Hasegawa, A. and Yanase, A. (1977) Energy Band Structure and Fermi Surface of LaB6 by a Self-Consistent APW Method. Journal of Physics F: Metal Physics, 7, 1245-1260. http://dx.doi.org/10.1088/0305-4608/7/7/023
- Walch, P.F., Ellis, D.E. and Mueller, F.M. (1977) Energy Bands and Bonding in LaB6 and YB6. Physical Review B, 15, 1859-1866. http://dx.doi.org/10.1103/PhysRevB.15.1859
- Johnson, R.W. and Daane, A.H. (1963) Electron Requirements of Bonds in Metal Borides. The Journal of Chemical Physics, 38, 425-432. http://dx.doi.org/10.1063/1.1733675
- Ott, H.R., Gavilano, J.L., Ambrosini, B., Vonlanthen, P., Felder, E., Degiorgi, L., Young, D.P., Fisk, Z. and Zysler, R. (2000) Unusual Magnetism of Hexaborides. Physical B: Condensed Matter, 281, 423-427.
- Denlinger, J.D., Clack, J.A., Allen, J.W., Gweon, G.-H., Poirier, D.M., Olson, C.G., Sarrao, J.L., Bianchi, A.D. and Fisk, Z. (2002) Bulk Band Gaps in Divalent Hexaborides. Physical Review Letters, 89, 157601. http://dx.doi.org/10.1103/PhysRevLett.89.157601
- Souma, S., Komatsu, H., Takahashi, T., Kaji, R., Sasaki, T., Yokoo, Y. and Akimitsu, J. (2003) Electronic Band Structure and Fermi Surface of CaB6 Studied by Angle-Resolved Photoemission Spectroscopy. Physical Review Letters, 90, 027202. http://dx.doi.org/10.1103/PhysRevLett.90.027202
- Kino, H., Aryasetiawan, F., van Schilfgaarde, M., Kotani, T., Miyake, T. and Terakura, K. (2002) GW Quasiparticle Band Structure of CaB6. Journal of Physics and Chemistry of Solids, 63, 1595-1597. http://dx.doi.org/10.1016/S0022-3697(02)00118-X
- Gao, S.-P., Jiang, J., Cao, M., Zhu, J. and Yuan, J. (2004) Unoccupied Electronic States in CaB6 Studied by Density Functional Theory and EELS Measurements. Physical Review B, 69, 214419. http://dx.doi.org/10.1103/PhysRevB.69.214419
- Helms, Z.M., Sen, P. and Mitas, L. (2005) Electronic Structure and Origin of Ferromagnetism in CaB6. http://arxiv.org/pdf/cond-mat/0509363.pdf
- Maiti, K. (2008) Role of Vacancies and Impurities in the Ferromagnetism of Semiconducting CaB6. Europhysics Letters, 82, 67006.
- Young, D.P., Hall, D., Torelli, M.E., Fisk, Z., Sarrao, J.L., Thompson, J.D., Ott, H.-R., Oseroff, S.B., Goodrich, R.G. and Zysler, R. (1999) High-Temperature Weak Ferromagnetism in a Low-Density Free-Electron Gas. Nature, 397, 412-414. http://dx.doi.org/10.1038/17081
- Fisk, Z., Ott, H.R., Barzykin, V. and Gor’kov, L.P. (2002) The Emerging Picture of Ferromagnetism in the Divalent Hexaborides. Physica B: Condensed Matter, 312, 808-810.
- Cho, B.K., Rhyee, J.-S., Oh, B.H., Jung, M.H., Kim, H.C., Yoon, Y.K., Kim, J.H. and Ekino, T. (2004) Formation of Midgap States and Ferromagnetism in Semiconducting CaB6. Physical Review B, 69, 113202. http://dx.doi.org/10.1103/PhysRevB.69.113202
- Hasegawa, A. and Yanase, A. (1979) Electronic Structure of CaB6. Journal of Physics C: Solid State Physics, 12, 5431-5440. http://dx.doi.org/10.1088/0022-3719/12/24/014
- Tromp, H.J., van Gelderen, P., Kelly, P.J., Brocks, G. and Bobbert, P.A. (2001) CaB6: A New Semiconducting Material for Spin Electronics. Physical Review Letters, 87, 016401. http://dx.doi.org/10.1103/PhysRevLett.87.016401
- Lee, B. and Wang, L.-W. (2005) Electronic Structure of Calcium Hexaborides. Applied Physics Letters, 87, 262509. http://dx.doi.org/10.1063/1.2150578
- Li, L.-H., Chen, L., Li, J.-Q. and Wu, L.-M. (2009) The First-Principles Study of Bulk CaB6 and the Field Emission of CaB6 Nanowires Using the HCTH Functional. The Journal of Physical Chemistry C, 113, 15384-15389. http://dx.doi.org/10.1021/jp901965y
- Xu, Y., Zhang, L., Cui, T., Li, Y., Xie, Y., Yu, W., Ma, Y. and Zou, G. (2007) First-Principles Study of the Lattice Dynamics, Thermodynamic Properties and Electron-Phonon Coupling of YB6. Physical Review B, 76, 214103. http://dx.doi.org/10.1103/PhysRevB.76.214103
- Xiao, L., Su, Y., Chen, H., Jiang, M., Liu, S., Hu, Z., Liu, R., Peng, P., Mu, Y. and Zhu, D. (2011) Study on the Electronic Structure and the Optical Performance of YB6 by the First-Principles Calculations. AIP Advances, 1, 022140.
- Sholl, D.S. and Steckel, J.A. (2009) Density Functional Theory—A Practical Introduction. Wiley, Hoboken. http://dx.doi.org/10.1002/9780470447710
- Martin, R.M. (2005) Electronic Structure—Basic Theory and Practical Methods. Cambridge University Press, Cambridge.
- Milman, V., Winkler, B., White, J.A., Pickard, C.J., Payne, M.C., Akhmatskaya, E.V. and Nobes, R.H. (2000) Electronic Structure, Properties, and Phase Stability of Inorganic Crystals: A Pseudopotential Plane-Wave Study. International Journal of Quantum Chemistry, 77, 895-910. http://dx.doi.org/10.1002/(SICI)1097-461X(2000)77:5<895::AID-QUA10>3.0.CO;2-C
- Kurth, S., Perdew, J.P. and Blaha, P. (1999) Molecular and Solid-State Tests of Density Functional Approximations: LSD, GGAs, and Meta-GGAs. International Journal of Quantum Chemistry, 75, 889-909. http://dx.doi.org/10.1002/(SICI)1097-461X(1999)75:4/5<889::AID-QUA54>3.0.CO;2-8
- Rydberg, H. (2001) Nonlocal Correlations in Density Functional Theory. Department of Applied Physics, Chalmers University of Technology and Göteborg University, Gothenburg.
- Mattsson, A.E., Schultz, P.A., Desjarlais, M.P., Mattsson, T.R. and Leung, K. (2005) Designing Meaningful Density Functional Theory Calculations in Materials Science—A Primer. Modelling and Simulation in Materials Science and Engineering, 13, R1-R31. http://dx.doi.org/10.1088/0965-0393/13/1/R01
- Perdew, J.P., Ruzsinszky, A., Tao, J., Staroverov, V.N., Scuseria, G.E. and Csonka, G.I. (2005) Prescription for the Design and Selection of Density Functional Approximations: More Constraint Satisfaction with Fewer Fits. The Journal of Chemical Physics, 123, 062201. http://dx.doi.org/10.1063/1.1904565
- Hafner, J.R., Wolverton, C. and Ceder, G. (2006) Toward Computational Materials Design: The Impact of Density Functional Theory on Materials Research. MRS Bulletin, 31, 659-668. http://dx.doi.org/10.1557/mrs2006.174
- Sousa, S.F., Fernandes, P.A. and Ramos, M.J. (2007) General Performance of Density Functionals. The Journal of Chemical Physics A, 111, 10439-10452. http://dx.doi.org/10.1021/jp0734474
- Janesko, B.G., Henderson, T.M. and Scuseria, G.E. (2009) Screened Hybrid Density Functionals for Solid-State Chemistry and Physics. Physical Chemistry Chemical Physics, 11, 443-454. http://dx.doi.org/10.1039/b812838c
- Goerigk, L. and Grimme, S. (2001) A Thorough Benchmark of Density Functional Methods for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. Physical Chemistry Chemical Physics, 13, 6670-6688. http://dx.doi.org/10.1039/c0cp02984j
- Cohen, A.J., Mori-Sanchez, P. and Yang, W. (2012) Challenges for Density Functional Theory. Chemical Reviews, 112, 289-320. http://dx.doi.org/10.1021/cr200107z
- Lejaeghere, K., Speybroeck, V.V., Oost, G.V. and Cottenier, S. (2014) Error Estimates for Solid-State Density-Functional Theory Predictions: An Overview by Means of the Ground-State Elemental Crystals. Critical Reviews in Solid State and Materials Sciences, 39, 1-24. http://dx.doi.org/10.1080/10408436.2013.772503
- Tanaka, K. and Onuki, Y. (2002) Observation of 4f Electron Transfer from Ce to B6 in the Kondo Crystal CeB6 and Its Mechanism by Multi-Temperature X-Ray Diffraction. Acta Crystallographica Section B, 58, 423-436. http://dx.doi.org/10.1107/S010876810102167X
- Funahashi, S., Tanaka, K. and Iga, F. (2010) X-Ray Atomic Orbital Analysis of 4f and 5d Electron Configuration of SmB6 at 100, 165, 230 and 298K. Acta Crystallographica Section B, 66, 292-306. http://dx.doi.org/10.1107/S0108768110009250
- Ammar, A., Menetrier, M., Villesuzanne, A., Matar, S., Chevalier, B. and Etourneau, J. (2004) Investigation of the Electronic and Structural Properties of Potassium Hexaboride, KB6, by Transport, Magnetic Susceptibility, EPR and NMR Measurements, Temperature-Dependent Crystal Structure Determination, and Electronic Band Structure Calculations. Inorganic Chemistry, 43, 4974-4987. http://dx.doi.org/10.1021/ic049444c
- Schmitt, K., Stuckl, C., Ripplinger, H. and Albert, B. (2001) Crystal and Electronic Structure of BaB6 in Comparison with CaB6 and Molecular [B6H6]−2. Solid State Sciences, 3, 321-327. http://dx.doi.org/10.1016/S1293-2558(00)01091-8
- Ishii, M., Aono, M., Muranaka, S. and Kawai, S. (1976) Raman Spectra of Metallic and Semiconducting Metal Hexaborides. Solid State Communications, 20, 437-440. http://dx.doi.org/10.1016/0038-1098(76)90544-5
- Yahia, Z., Turrell, S., Turrell, G. and Mercurio, J.P. (1990) Infra-Red and Raman Spectra of Hexaborides: Force-Field Calculations and Isotopic Effects. Journal of Molecular Structure, 224, 303-312. http://dx.doi.org/10.1016/0022-2860(90)87025-S
- Souma, S., Komoda, H., Iida, Y., Sato, T., Takahashi, T. and Kunii, S. (2005) Direct Observation of Superconducting Gap in YB6 by Ultrahigh-Resolution Photoelectron Spectroscopy. Journal of Electron Spectroscopy and Related Phenomena, 144-147, 503-506. http://dx.doi.org/10.1016/j.elspec.2005.01.125
- Kunii, S., Kasuya, T., Kadowaki, K., Date, M. and Woods, S.B. (1984) Electron Tunneling into Superconducting YB6. Solid State Communications, 52, 659-661. http://dx.doi.org/10.1016/0038-1098(84)90728-2
- Mott, S.N. (1974) Metal-Insulator Transitions. Taylor and Francis Ltd., London.


