Modeling and Numerical Simulation of Material Science
Vol. 2 No. 3 (2012) , Article ID: 21378 , 8 pages DOI:10.4236/mnsms.2012.23005
Adaptive Neuro-Fuzzy Inference System for Prediction of Effective Thermal Conductivity of Polymer-Matrix Composites
Thermal Physics Laboratory, Department of Physics, University of Rajasthan, Jaipur, India
Email: singhrvs@rediffmail.com, singhrajpal7@gmail.com
Received February 14, 2012; revised March 23, 2012; accepted April 5, 2012
Keywords: Neuro-Fuzzy Inference System; Effective Thermal Conductivity; Polymer Composites; Volume Fraction; Fuzzy Inference Systems
ABSTRACT
In the present study, the adaptive neuro-fuzzy inference system (ANFIS) is developed for the prediction of effective thermal conductivity (ETC) of different fillers filled in polymer matrixes. The ANFIS uses a hybrid learning algorithm. The ANFIS is a class of adaptive networks that is functionally equivalent to fuzzy inference systems (FIS). The ANFIS is based on neuro-fuzzy model, trained with data collected from various sources of literature. ETC is predicted using ANFIS with volume fraction and thermal conductivities of fillers and matrixes as input parameters, respectively. The predicted results by ANFIS are in good agreements with experimental values. The predicted results also show the supremacy of ANFIS in comparison with other earlier developed models.
1. Introduction
The use of computer based modeling techniques is extensive in science and engineering research during these days. Polymer composites with high thermal conductivity and low dielectric constant are highly desirable for use in various applications, such as electric stress control, electromagnetic shielding, and higher storage capability of the electric energy. The process ability and other physicochemical properties of the polymer composites are more advantageous for practical applications compared to ceramic materials. Modern demands require smaller size of packages and higher power of electronic devices. Polymer matrixes are commonly used such as polyethylene, polypropylene, polyurethane, polyvinyl chloride etc. which are good thermally and electrically insulators. Due to the increasing use of composite materials in many industrials sectors, including transformation, electronic, and energy supply and production, there is a renewed interest in simulation techniques to estimate the ETC of fiber and particle filled polymer composites. Dependence of the ETC of these materials on porosity, shape factor and packing of the particles is a matter of concern to engineers, mathematicians, and physicists. A number of experimental studies have been carried out, and various numerical and analytical models have been developed to predict the effective thermal conductivity of particle filled polymer composites. Thermal conductivity of boron nitride (BN) reinforced high density polyethylene (HDPE) composites was investigated under a special dispersion state of BN particles in HDPE, and together with the influence on thermal conductivity of particle sizes of filler used by Zhou et al. [1]. Luyt et al. [2] investigated the thermal, mechanical and electrical properties of copper powder filled polyethylene composites. The influence on these properties of the amount of copper powder in the polymer matrix was discussed. Xu et al. [3] investigated the use of aluminum nitride (AlN) in the form of AlN whiskers, with and without the presence of AlN particles and by the use of AlN whiskers and particles, and polyvinylidene fluoride (PVDF) as the matrix. Then a thermal conductivity up to 11.5 W/m K was obtained. Gu et al. [4] investigated the content of AlN influencing the thermal conductivity and ultimate mechanical properties of AlN/ linear low-density polyethylene (LLDPE) composites. Chemical surface treatment of AlN with titanate coupling reagent of NDZ-105 was used to improve thermal conductivity by minimizing the interfacial phonon scattering, and to increase the mechanical strength of composites by improving the wet ability and uniform dispersion of AlN in the LLDPE.
Maxwell [5] calculated the ETC of a random distribution of spheres in a continuous medium which worked well for low concentrations by solving Laplace’s equation and assuming absence of any interactions between the filler particles. Hamilton and Crosser [6] extended Maxwell’s model to include an empirical factor n to account for the shape of the particles (n = 3 for spheres, and n = 6 for cylinder). Singh et al. [7] developed an empirical relation for quick estimation of ETC of highly porous systems. In order to incorporate varying individual geometries and non-linear flow of heat flux lines generated by the difference in thermal conductivity of the constituent phases, a correlation term has been introduced. ETC of polymer composites that contain high-density polyethylene with spherical inclusions is investigated theoretically by Singh and Sharma [8]. Rajinder Pal [9] evaluated the Lewis-Nielson model in light of a vast amount of experimental data available on thermal and electrical conductivities of particulate composites. Rajinder Pal [10] developed three new models for the ETC of concentrated particulate composites by using the differential effective medium approach. Singh et al. [11] explored the influence of the some parameter, which has been obtained using the laws of statistical mechanics. Equivalent thermal resistor formed out of the phases in the form of parallel slabs and the resistor model approach has been applied. Boudenne et al. [12] studied the thermal parameters of composite materials. A nonlinear least-squares criterion is used on experimental transfer functions to identify the thermal conductivity and the diffusivity of aluminum-polymer composite materials. Kumlutas et al. [13,14] measured the ETC of high density polyethylene containing particulate fillers by a hotwire technique and numerically calculated by finite difference method. Serkan et al. [15] investigated the ETC of copper powder filled polyamide composites in the range of filler content 0% - 30% by volume for particle shape of short fibers and 0% - 60% by volume for particle shapes of plates and spheres, which was measured by the hot-disk method. Dey et al. [16] reported the thermal conductivity and coefficient of thermal expansion of silicon particulates reinforced HDPE composites. Wang et al. [17] predicted the effective physical properties of complex multiphase materials developing the random generation-growth algorithm for reproducing multiphase microstructures, statistically equivalent to the actual systems. Then a high-efficiency lattice Boltzmann solver for the corresponding governing equations was described which, while assuring energy conservation and the appropriate continuities at numerous interfaces in a complex system, and demonstrated its numerical power in yielding accurate solutions. Wang et al. [18] presented the two-dimensional (2D) results of mesoscopic simulations addressing the influence of fiber orientation angle, fiber length, mean porosity, and the fiber location distribution function on the effective thermal conductivity.
Since the early 1990s, artificial neural networks (ANNs) have been of interest for many researchers and they applied it successfully to almost every problem in geotechnical and in thermal engineering. ANNs are thus well suited for modeling the complex behavior of porous materials. In the last few years, many researchers used artificial neural network approach to predict thermo-physical coefficients in different areas. Recently, Singh et al. [19] and Bhoopal et al. [20] have applied ANN approach successfully to predict the ETC of various complex systems. Gotlib et al. [21], Zhang and Friedrich [22] and Turias et al. [23] have also predicted various properties with the help of ANN approach Kadi [24] studied the mechanical behavior of fiber-reinforced polymeric composite by using artificial neural networks. Al-Haik et al. [25] predicted the non-linear viscoelastic behavior of polymer composites using artificial neural network.
There are few studies on thermal conductivity of metal/non-metal filled polymer composites, which would have demanded the value of effective thermal conductivity of polymers. Adaptive neuro-fuzzy inference system (ANFIS) has recently been introduced to predict the effective thermal conductivity of metal/non-metal filled polymer composites. The fillers used most frequently are particles of carbon, aluminum, copper, brass, graphite and magnetite. By the addition of fillers to polymer matrix the thermal conductivity of polymers can be increased remarkably. In this study, high-density polyethylene (HDPE), low-density polyethylene (LDPE), linear lowdensity polyethylene (LLDPE), and polyvinylidene fluoride (PVDF) with different metals/non-metals such as boron nitride (BN), copper (Cu) and aluminum nitride (AIN) are used as inclusions [1-4], because of its superior mechanical and physical properties. HDPE is one of the most widely used commercial polymers. However, its toughness, weather resistance, and environmental stress cracking resistance are not good enough which limits its applications in many high-technology areas. Reinforcing HDPE with fillers (viz., aluminum and copper particles, short carbon fibers, carbon, graphite, aluminum nitrides and magnetic particles) has been found to improve its properties. Low-density polyethylene (LDPE) is a thermoplastic made from petroleum. Compared with LDPE, LLDPE possesses better strength, toughness, heat-resistance, cold resistance, environmental stress cracking resistance, and tearing resistance properties.
In this perspective, an attempt has been made to formulate a rule-based model for prediction of the ETC of polymer composites using an adaptive neuro-fuzzy inference system, (ANFIS). Rule-based modeling, specifically using fuzzy logic rule is a soft-computing tool-based approach to construct a model for the systems that are highly complex and exhibit non-linear behaviour in nature, for which no well-defined mathematical expression(s) exist. The effectiveness of the ANFIS approach is extensively tested by comparing its results with those obtained in real experimentations as well as with those of various existing empirical/semi-empirical models reported in literature.
2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
ANFIS modeling is based on conventional mathematical tools. This modeling is also known as fuzzy modeling or fuzzy identification. First of all, this system modeling was explored systematically by Takagi and Sugeno [26]. The ANFIS was developed in the early 90s by Jang [27], which combines the concepts of fuzzy logic and neural networks to form a hybrid intelligent system that enhances the ability to learn automatically and adapt. Hybrid systems have been used by researchers for modeling and predictions in various engineering systems. There are some basic aspects of this system which are in need of better understanding. More specifically: 1) No standard methods exist for transforming human knowledge or experience into the rule base and data base of a fuzzy inference system (FIS); 2) There is a need for effective methods form tuning the membership functions (MFs) so as to minimize the output error measure or maximize performance index.
2.1. Fuzzy Inference Systems (FISs)
FISs are also known as fuzzy-rule-based systems, fuzzy models, fuzzy associative memories (FAM), or fuzzy controller when used as controllers. Basically a FIS is composed of five functional blocks which is show in Figure 1.
1) A rule base containing a number of fuzzy if-then rule;
2) A data base which defines the membership functions of the fuzzy sets used in the fuzzy rules;
3) A decision making unit which performs the inference operations on the rules;
4) A fuzzification interface which transforms the crisp inputs into degrees of match with linguistic values;
5) A defuzzification interface which transforms the fuzzy results of the inference into a crisp output.
Given below are the steps of fuzzy reasoning performed by FISs:
1) Compare the input variables with the MFs on the premise part to obtain the membership values of each linguistic label. This step is called fuzzification;
2) Combine the membership values on the premise part to get firing strength (weight) of each rule;
3) Generate the qualified consequent of each rule depending on the firing strength;
4) Aggregate the qualified consequents to produce a crisp output. This step is called defuzzification.

Figure 1. Fuzzy Inference System.
2.2. Architecture and Basic Learning Rule: Adaptive Networks
An adaptive network is a multilayer feedforward network. The basic learning rule of adaptive networks is based on the gradient descent and the chain rule, which was proposed by Werbos [28] in the 1970’s. An Adaptive network is in fact a superset of all kinds of feedforward neural network (FNN) with supervised learning capability. An adaptive network structure is consisting of nodes and directional links through which the nodes are connected. Moreover, all of the nodes are adaptive, which means their outputs depend on the parameters pertaining to these nodes, and the learning rule specifies how these parameters should be changed to minimize a prescribed error measure. The formulas for the node functions may vary from node to node, and the choice of each node function depends on the overall input-output function which the adaptive network is required to carry out. For a given adaptive network with L layers and pth layer with # (p) nodes, the nodes in the ith position of the kth layer by (p, i), and its node function by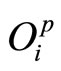 .
.
As the node output depends upon the inputs and its parameter sets
 (1)
(1)
where a, b, c etc., are the parameters pertaining to this node.  both are used as the node output and the node function. Assuming the given training data set has K entries, the error measure or energy functions for kth
both are used as the node output and the node function. Assuming the given training data set has K entries, the error measure or energy functions for kth 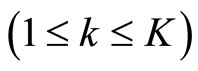 entry of training data entry as the sum of squared error:
entry of training data entry as the sum of squared error:
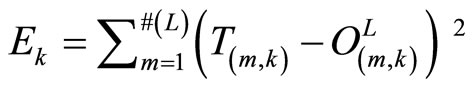 (2)
(2)
where 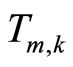 is the mth component of kth target output vector, and
is the mth component of kth target output vector, and ![]() is the mth component of actual output vector produced by the presentation of the kth input vector. Hence, the overall error measure is:
is the mth component of actual output vector produced by the presentation of the kth input vector. Hence, the overall error measure is:
 (3)
(3)
Next for the development of a learning procedure that implements gradient descents in E over the parameter space, the error rate is:
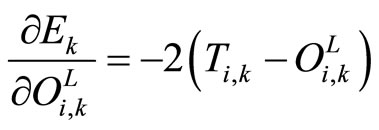 (4)
(4)
For the internal node at (p, i), the error rate is derived by the chain rule:
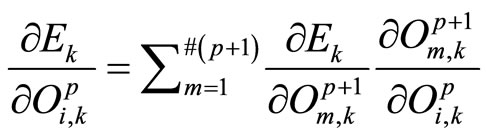 (5)
(5)
where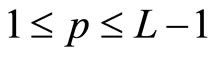 . That is, the error rate of an internal node can be expressed as a linear combination of the error rates of the nodes in the next layer. Therefore, for all
. That is, the error rate of an internal node can be expressed as a linear combination of the error rates of the nodes in the next layer. Therefore, for all 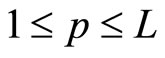 and
and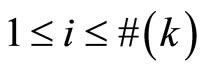 , we can find
, we can find  by
by
(4) and (5).
Now if ![]() is a parameter of the given adaptive network then:
is a parameter of the given adaptive network then:
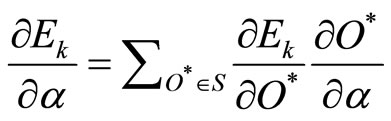 (6)
(6)
where S is the set of nodes whose outputs depend on![]() . Then the derivative of the over all error measure E with respect to
. Then the derivative of the over all error measure E with respect to ![]() is
is
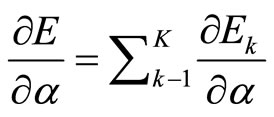 (7)
(7)
Accordingly, the update formula for the generic parameter ![]() is:
is:
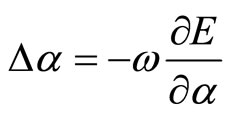 (8)
(8)
where ![]() is a learning rate.
is a learning rate. ![]() can be further expressed as:
can be further expressed as:
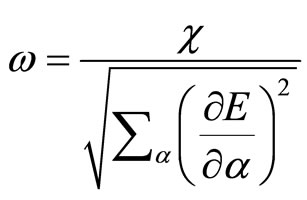 (9)
(9)
where 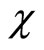 is the step size, the length of each gradient transition in the parameters space.
is the step size, the length of each gradient transition in the parameters space.
3. Results and Discussion
In the present calculations, the activation (threshold) functions used for the network are: Tangent sigmoid function (TANSIG), which is non-linear function given by
 (10)
(10)
and pure linear function (PURELIN), where linear function is
 (11)
(11)
MATLAB function ANFIS with a hybrid-learning algorithm to identify the Generalized bell-shaped built-in membership function parameters of (Genfis1) single-output, Sugeno type fuzzy inference systems (FIS) is used. Generalized bell-shaped built-in membership function (gbellmf) depends on three parameters a, b, and c as given by
 (12)
(12)
where the parameter b is usually positive. The parameter c locates the center of the curve.
A combination of least squares and backpropagation gradient descent methods is used for training FIS membership function parameters to model a given set of input/output data. These data are collected from various sources of literature. Proper selection of the input data plays a key role to the ANFIS approach and can be of help to reach a satisfactory predictive quality. The first data set is used to train/learn the system. The second data set, which does not include any data from the first data set, is used to test ANFIS’s generalization ability. ANFIS programming in MATLAB R2010b software has been used in this study. The ANFIS has provided better results for prediction of the effective thermal conductivity of metal/non-metal filled polymer composites and better agreement with the available experimental data.
3.1. Effective Thermal Conductivity of HDPE/BN Composite
Figure 2 shows the variation in experimental values of effective thermal conductivity of HDPE/BN composites [1] and those predicted by the ANFIS, and other theoretical models [5-7] with volume fraction of dispersed phase (filler). It is seen that with the increase in filler loading the ETC of the composite increases. The ETC of 1.14 W/m K is achieved by ANFIS for HDPE containing 30% volume fraction of BN, more than four times of pure HDPE. Therefore, the addition of filler (BN) into HDPE matrix would increase the ETC, and the content of filler has an effect on the ETC of the composites. The enhancement in the effective thermal conductivity of HDPE/BN composites is expected, as the thermal conductivity of the filler (BN) is significantly higher (λBN = 33 W/m K) than that of pure HDPE (λHDPE = 0.26 W/m K). With the increase in volume content of BN in HDPE, the interaction between BN particles increases and they come in contact with each other, resulting in the ease in
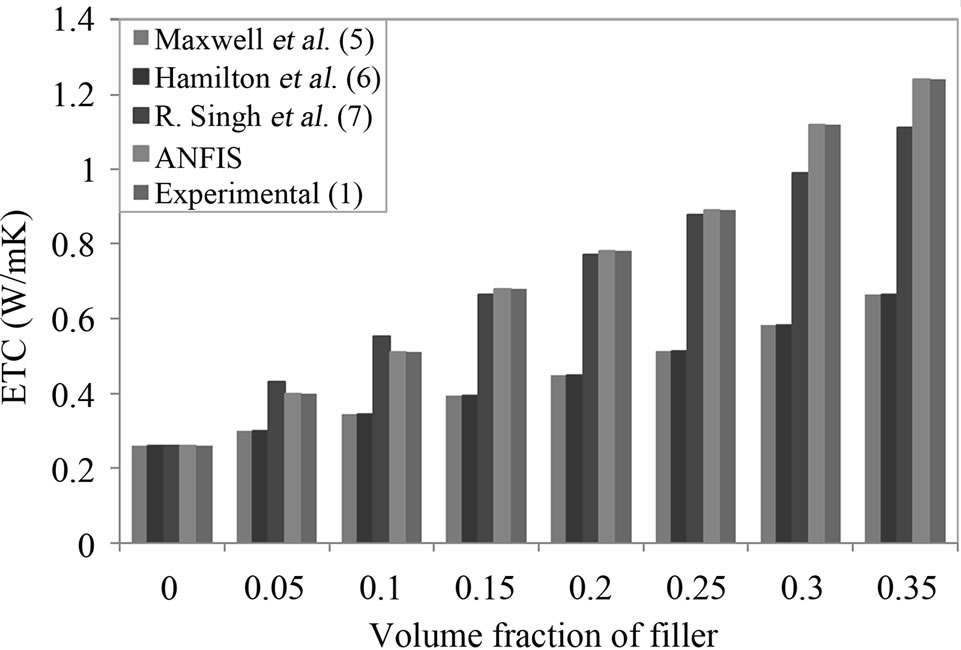
Figure 2. The variation of ETC of HDPE/BN composites with volume fraction of filler.
the transfer of heat and consequent enhancement of ETC. Most of models fail to predict the ETC of HDPE/BN composites over the entire range of filler concentration used in the present study. It may be noted that calculated results of Maxwell and Hamilton and Crosser model [5-6] of equations largely deviate from the ANFIS and experimental data over a wide range of volume fraction of dispersed phase (filler) between 0% to 35%.In the present case, the ETC calculated by Singh et al. [7], which is extremely well with the experimental and ANFIS results of HDPE/BN composites.
3.2. Effective Thermal Conductivity of LDPE and LLDPE/Cu Composite
Figures 3 and 4 show the experimental values of effective thermal conductivity of LDPE and LLDPE/copper composites [2] and those predicted by the ANFIS and other theoretical models [5-7] over a wide range of volume fraction of dispersed phase (filler) between 0% to 24%. It is clear that the effective thermal conductivities
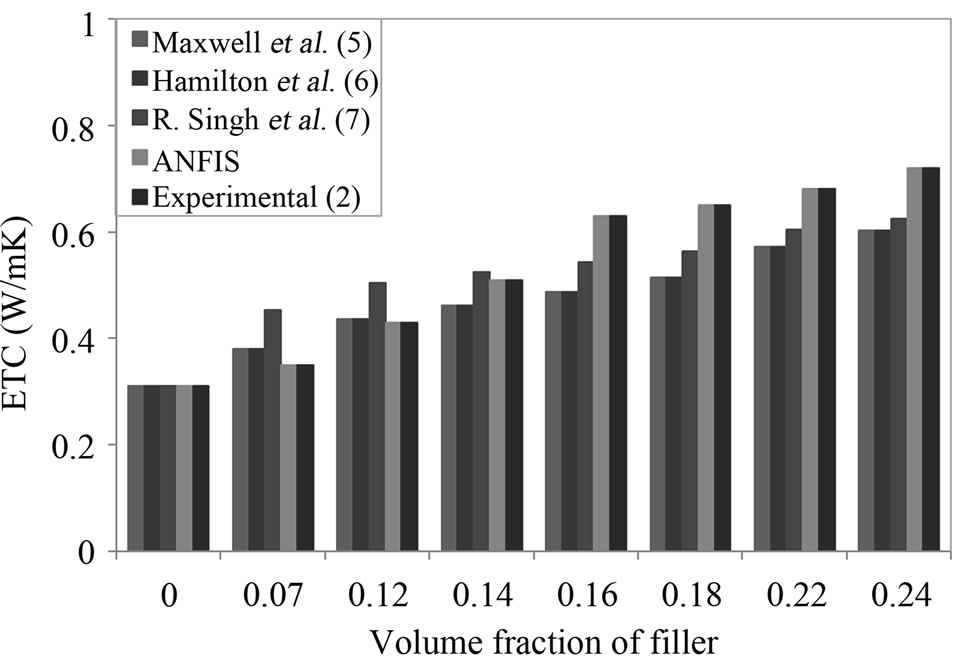
Figure 3. The variation of ETC of LDPE/Cu composites with volume fraction of filler.
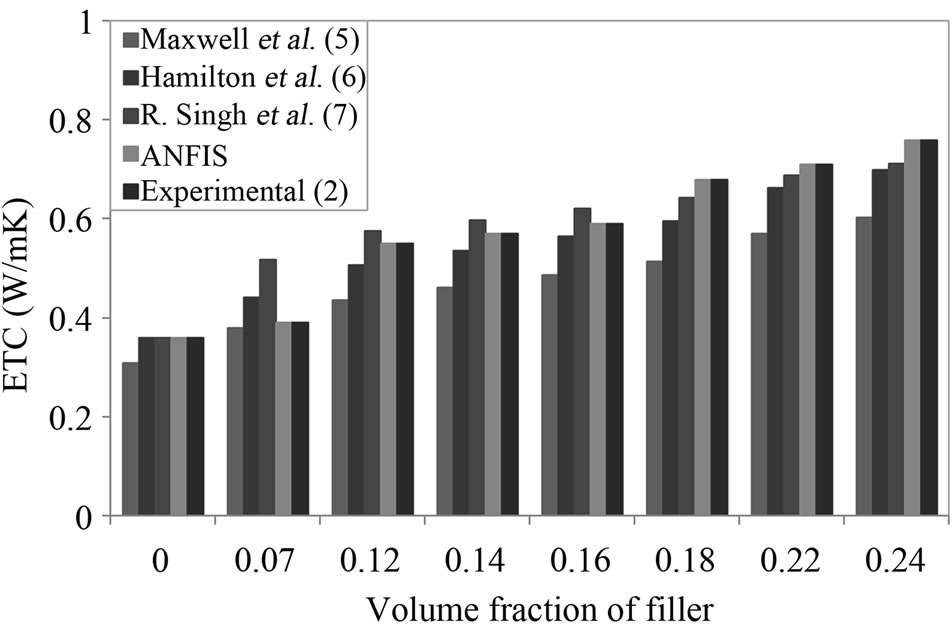
Figure 4. The variation of ETC of LLDPE/Cu composites with volume fraction of filler.
of the composites are higher than that of the both LDPE and LLDPE matrix. It is found that with the increase in the filler loading, the effective thermal conductivity of the composite increases. The maximum values of ETC 0.72 W/m K and 0.76 W/m K are obtained for LDPE and LLDPE containing 24% volume fraction of copper, respectively. This enhancement in ETC is mainly due to a significantly higher thermal conductivity of the filler (copper) (λcopper = 394 W/m K) than that of LDPE (λLDPE = 0.31 W/m K) and LLDPE (λLLDPE = 0.36 W/m K). The ETC is higher in the LLDPE matrix than in the LDPE matrix for all copper contents. The calculated results of Singh et al. [7] equations are excellent agreement with the experimental and ANFIS results. The Maxwell and Hamilton and Crosser models [5,6] calculated fairly well the ETC values only for low concentration of fillers. The reason is probably that more conductive paths are created as a consequence of higher agglomeration of particles [29]. Since the copper particles are restricted to the amorphous parts of polymer, and since LLDPE has lower amorphous content, it is quite possible that there will be more agglomeration of particles in the LLDPE matrix.
3.3. Effective Thermal Conductivity of PVDF/AlN Composite
The effective thermal conductivity of PVDF/AlN composites with volume fraction of dispersed phase (filler) over the range between 0% to 73% is shown in Figure 5. It is noticed that the effective thermal conductivity of the composite increases with the increase in filler loading, except that the ETC decreased when the AlN volume fraction is increased from 70% to 73% (due to increase in porosity). The highest values of effective thermal conductivity 4.811 W/m K and 3.722 W/m K are predicted by ANFIS for PVDF containing 70% and 73% volume fraction of AlN, respectively. The enhancement in the ETC of PVDF/AlN composites is expected, as the thermal
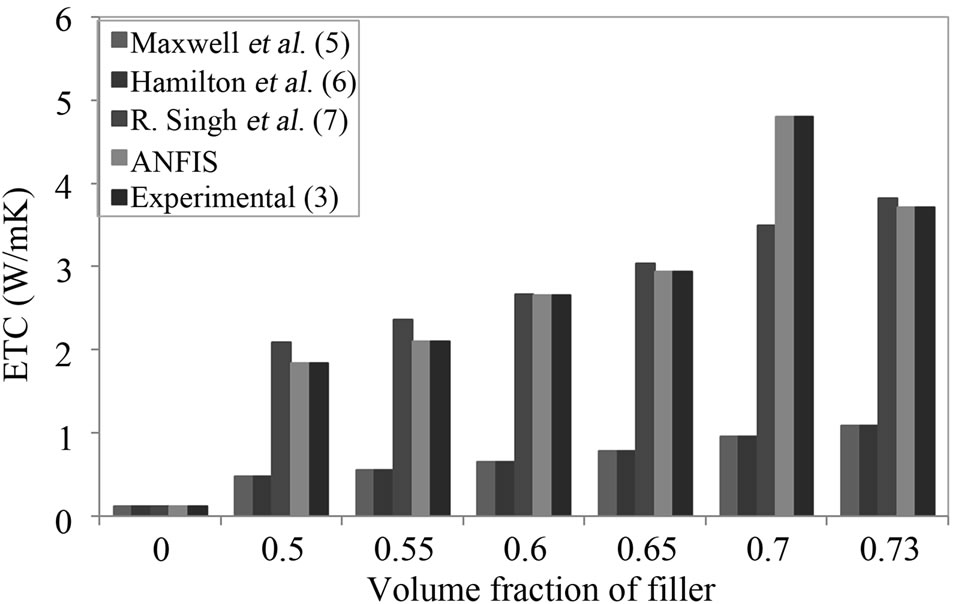
Figure 5. The variation of ETC of PVDF/AlN composites with volume fraction of filler.
conductivity of the filler (AlN) is significantly higher (λAlN = 320 W/m K) than that of PVDF (λPVDF = 0.12 W/m K). The Maxwell and Hamilton and Crosser models [5,6] are failed to calculate the ETC of PVDF/AlN composites over the entire range of filler concentration. It is also shown that the calculated results by the Singh et al. [7] equations are in better agreement with the experimental [3] and ANFIS results.
3.4. Effective Thermal Conductivity of LLDPE/AlN Composite
Figure 6 shows the variation in experimental ETC of LLDPE/AlN composites [4] over a wide range of volume fraction of dispersed phase (filler) between 0% to 30% and those predicted by the ANFIS and calculated by various model with volume fraction of dispersed (filler) phase. It is clear that the effective thermal conductivities of composites are higher than that of pure LLDPE matrix. The ETC of composites increases considerably with the increase of volume fractions of inclusions. The maximum value of effective thermal conductivity 1.0842 W/m K is achieved by ANFIS for LLDPE containing 30% volume fraction of AlN. This enhancement in the ETC of LLDPE/AlN composites is mainly because the thermal conductivity of filler (AlN) is significantly higher (λAIN = 320 W/m K) than that of LLDPE (λLLDPE = 0.36 W/m K).From the figure, it can be observed that the calculations of the Maxwell and Hamilton and Crosser models [5,6] are mismatched significantly, while the calculated results by Singh et al. model [7] of equations are satisfactory in agreement with the experimental [4] and ANFIS results.
In Figures 2-6, it is noticed that the ETC of different metal/non-metal filled polymer composites increases with the increase in volume contents of filler in polymer composites. The enhancement in the effective thermal conductivity of present composites with increase in volume
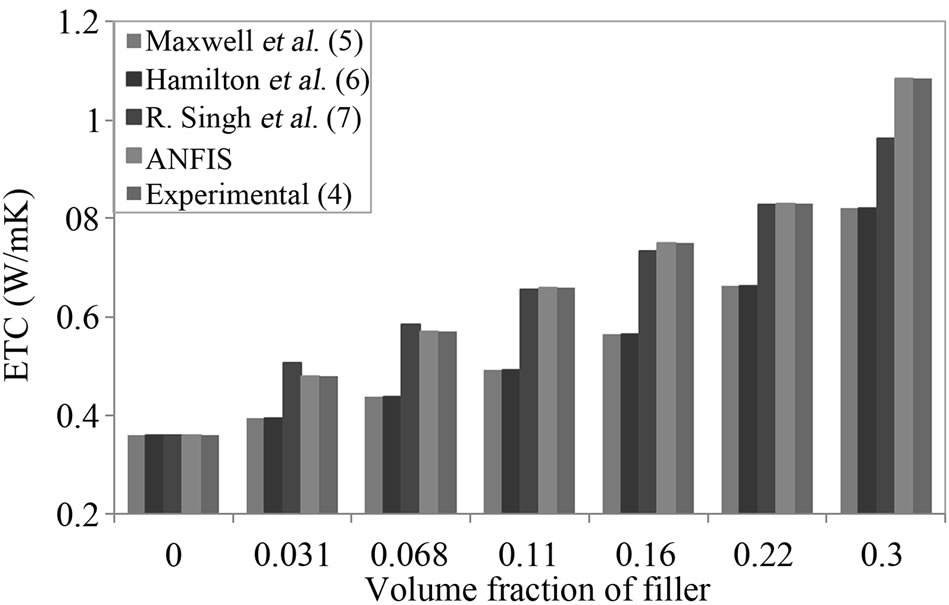
Figure 6. The variation of ETC of LLDPE/AlN composites with volume fraction of filler.
content of metal/non-metal is mainly due to more interaction between metal/non-metal particles as they come in contact with each other, resulting in the ease in transfer of heat and consequent enhancement of the effective thermal conductivity. Highly conductive different metal/ non-metal like BN, Cu, and AlN are used as fillers into polyethylene (HDPE, LDPE, and LLDPE) and polyvinylidene fluoride (PVDF) composites as matrix in this study [1-4]. All the predictions of the ETC by ANFIS are in good agreement with the available experimental results and calculated by the Singh et al. model [7]. Maxwell as well as Hamilton and Crosser models [5,6] are calculated fairly well the ETC only for low concentration of present composites.
Clearly, there are many benefits of using ANFIS for prediction, including the following: 1) It is a general framework that combines two technologies, namely neural networks and fuzzy systems; 2) By using fuzzy techniques, both numerical and linguistic knowledge can be combined into a fuzzy rule base; 3) The combined fuzzy rule base represents the knowledge of the network structure so that structure learning techniques can easily be accomplished; 4) Fuzzy membership functions can be tuned optimally by using learning methods; 5) The architecture requirements are fewer and simpler compared to neural networks, which require extensive trails and errors for optimization of their architecture; and 6) ANFIS does not require extensive initializations through several random starts before training, as always happens in neural networks. Other advantages of the two-phase neuro fuzzy hybrid technique in the ANFIS model also include its nonlinear ability, its capacity for fast learning from numerical and linguistic knowledge, and its adaptation capability.
4. Conclusion
We have described the architecture of adaptive network based fuzzy inference system (ANFIS). By employing a hybrid learning procedure, the proposed architecture can refine fuzzy if-then rules obtained from human experts to describe the input-output behavior of a complex system. The predicted results show that using a hybrid intelligent approach, in particular ANFIS, gives good prediction accuracies for the ETC of metal/non-metal filled polymer composites. The resultant predictions of effective thermal conductivity by the ANFIS agree well with the available experimental data. The ANFIS exhibit the capability to use for the predictions of effective thermal conductivity of various types of tailored complex materials.
REFERENCES
- W. Zhou, S. Qi, H. Li and S. Shao, “Study on Insulating Thermal Conductive BN/HDPE Composites,” Thermochimica Acta, Vol. 45, No. 1, 2007, pp. 36-42. doi:10.1016/j.tca.2006.10.018
- A. S. Luyt, J. A. Molefi and H. Krump, “Thermal, Mechanical and Electrical Properties of Copper Powder Filled Low-Density and Linear Low-Density Polyethylene Composites,” Polymer Degradation and Stability, Vol. 91, No. 7, 2006, pp. 1629-1636. doi:10.1016/j.polymdegradstab.2005.09.014
- Y. Xu, D. D. L. Chung and C. Morz, “Thermally Conducting Aluminum Nitride Polymer—Matrix Composites,” Composites Part A: Applied Science and Manufacturing, Vol. 32, No. 12, 2001, pp. 1749-1757. doi:10.1016/S1359-835X(01)00023-9
- J. Gu, Q. Zhang, J. Dang, J. Zhang and Z. Yang, “Thermal Conductivity and Mechanical Properties of Aluminum Nitride Filled Linear Low-Density Polyethylene Composites,” Polymer Engineering & Science, Vol. 49, No. 5, 2009, pp. 1030-1034. doi:10.1002/pen.21336
- J. C. Maxwell, “A Treatise on Electricity and Magnetism,” 3rd Edition, Dover Publications, New York, 1954.
- R. L. Hamilton and O. K. Crosser, “Thermal Conductivity of Heterogeneous Two-Component Systems,” Industrial & Engineering Chemistry Fundamentals, Vol. 1, No. 3, 1962, pp. 187-191. doi:10.1021/i160003a005
- R. Singh and H. S. Kasana, “Computational Aspects of Effective Thermal Conductivity of Highly Porous Metal Foams,” Applied Thermal Engineering, Vol. 24, No. 13, 2004, pp. 1841-1849. doi:10.1016/j.applthermaleng.2003.12.011
- R. Singh and P. Sharma, “Effective Thermal Conductivity of Polymer Composites,” Advanced Engineering Materials, Vol. 10, No. 4, 2008, pp. 366-370. doi:10.1002/adem.200700336
- R. Pal, “On the Lewis-Nielson Model for Thermal/Electrical Conductivity of Composites,” Composites Part A: Applied Science and Manufacturing, Vol. 39, No. 5, 2008, pp. 718-726. doi:10.1016/j.compositesa.2008.02.008
- R. Pal, “New Model for Thermal Conductivity of Particulate Composites,” Journal of Reinforced Plastics and Composites, Vol. 26, No. 7, 2007, pp. 643-651. doi:10.1177/0731684407075569
- R. Singh, P. K. Sharma and R. S. Bhoopal, “Prediction of Effective Thermal Conductivity of Cellular and Polymer Composites,” Indian Journal of Pure Applied Physics, Vol. 49, No. 5, 2011, pp. 344-349.
- A. Boudenne, L. Ibos, M. Fois and E. Gehin, “Thermophysical Properties of Polypropylene/Aluminum Composites,” Journal of Applied Polymer Science, Vol. 42, No. 4, 2004, pp. 722-732.
- D. Kumlutas, I. H. Tavman and M. T. Coban, “Thermal Conductivity of Particle Filled Polyethylene Composite Materials,” Composites Science and Technology, Vol. 63, No. 1, 2003, pp. 113-117. doi:10.1016/S0266-3538(02)00194-X
- D. Kumlutas and I. H. Tavman, “A Numerical and Experimental Study on Thermal Conductivity of Particle Filled Polymer Composites,” Journal of Thermoplastic Composite Materials, Vol. 19, No. 4, 2006, pp. 441-455. doi:10.1177/0892705706062203
- H. Serkan, D. Kumlutas and I. H. Tavman, “Effect of Particle Shape on Thermal Conductivity of Copper Reinforced Polymer Composites,” Journal of Reinforced Plastics and Composites, Vol. 26, No. 1, 2007, pp. 113-121. doi:10.1177/0731684407072522
- T. K. Dey and M. Tripathi, “Thermal Properties of Silicon Powder Filled High-Density Polyethylene Composites,” Thermochimica Acta, Vol. 502, No. 1-2, 2010, pp. 35-42. doi:10.1016/j.tca.2010.02.002
- M. Wang and N. Pan, “Predictions of Effective Physical Properties of Complex Multiphase Materials,” Materials Science and Engineering: R, Vol. 63, No. 1, 2008, pp. 1- 30.
- M. Wang, J. Heb, J. Yu and N. Pan, “Lattice Boltzmann Modeling of the Effective Thermal Conductivity for Fibrous Materials,” International Journal of Thermal Sciences, Vol. 46, No. 9, 2007, pp. 848-855. doi:10.1016/j.ijthermalsci.2006.11.006
- R. Singh, R. S. Bhoopal and S. Kumar, “Prediction of Effective Thermal Conductivity of Moist Porous Materials Using Artificial Neural Network Approach,” Building & Environment, Vol. 46, No. 12, 2011, pp. 2603-2608. doi:10.1016/j.buildenv.2011.06.019
- R. S. Bhoopal, P. K. Sharma, S. Kumar, A. Pandey, R. S. Beniwal and R. Singh, “Prediction of Effective Thermal Conductivity of Polymer Composites Using Artificial Neural Network Approach,” Special Topics & Review in Porous Media—An International Journal, Vol. 3, No. 2, 2012, pp. 115-123.
- V. A. Gotlib, T. Sato and A. I. Beltzer, “Neural Computing of Effective Properties of Random Composite Materials,” Computer Structure, Vol. 79, No. 1, 2001, pp. 1-6. doi:10.1016/S0045-7949(00)00134-6
- Z. Zhang and K. Friedrich, “Artificial Neural Networks Applied to Polymer Composites: A Review,” Composites Science and Technology, Vol. 63, No. 14, 2003, pp. 2029- 2044. doi:10.1016/S0266-3538(03)00106-4
- I. J. Turias, J. M. Gutierrez and P. L. Galindo, “Modeling the Effective Thermal Conductivity of an Unidirectional Composite by the Use of Artificial Neural Networks,” Composites Science and Technology, Vol. 65, No. 3-4, 2005, pp. 609-619. doi:10.1016/j.compscitech.2004.09.018
- H. El Kadi, “Modeling the Mechanical Behavior of Fiber-Reinforced Polymeric Composite Materials Using Artificial Neural Network—A Review,” Composite Structure, Vol. 73, No. 1, 2006, pp. 1-23. doi:10.1016/j.compstruct.2005.01.020
- M. S. AI-Haik, M. Y. Hussaini and H. Garmestani, “Prediction of Non-Linear Viscoelastic Behavior of Polymeric Composites Using an Artificial Neural Network,” International Journal of Plasticity, Vol. 22, No. 7, 2006, pp. 1367-1392. doi:10.1016/j.ijplas.2005.09.002
- T. Takagi and M. Sugeno, “Fuzzy Identification of System and Its Applications to Modelling and Control,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 15, No. 1, 1985, pp. 116-132.
- J. S. R. Jang, “ANFIS: Adaptive-Network-Based Fuzzy Inference System,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 23, No. 3, 1993, pp. 665-685. doi:10.1109/21.256541
- P. Werbos, “New Tools for Prediction and Analysis in the Behavioral Sciences,” Ph.D. Dissertation, Harvard University, Cambridge, 1974.
- I. Krupa and I. Chodak, “Physical Properties of Thermoplastic/Graphite Composites,” European Polymer Journal, Vol. 37, No. 11, 2001, pp. 2159-2168. doi:10.1016/S0014-3057(01)00115-X

