Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.04(2017), Article ID:78773,19 pages
10.4236/jhepgc.2017.34041
Reconsidering “Does the Sum Rule Hold at the Big Bang?” with Pre Planckian HUP, and Division Algebras
Andrew W. Beckwith
Physics Department, College of Physics, Chongqing University, Chongqing, China

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 15, 2017; Accepted: August 26, 2017; Published: August 29, 2017
ABSTRACT
In 2012, the author submitted an article to the Prespacetime Journal based upon the premise of inquiry as to the alleged vanishing of disjoint open sets contributing to quantum vector measures no longer working, i.e. the solution in 2012 was that the author stated that quantum measures in 4 dimensions would not work, mandating, if measure theory were used, imbedding in higher dimensions was necessary for a singularity. The idea was to use the methodology of String Theory as to come up with a way out of the impasse if higher dimensions do not exist. We revisit this question, taking into account a derived HUP, for metric tensors if we look at Pre-Planckian space-time introducing a pre-quantum mechanical HUP which may be a way to ascertain a solution not mandating higher dimensions, as well as introducing cautions as to what will disrupt the offered solution. Note that first, measurable spaces allow disjoint sets. Also, that smooth relations alone do not define separability or admit sets Planck’s length, if it exists, is a natural way to get about the “bad effects” of a cosmic singularity at the beginning of space-time evolution, but if a development is to be believed, namely by Stoica in the article, about removing the cosmic singularity as a breakdown point in relativity, there is nothing which forbids space-time from collapsing to a point. Without the use of a Pre Planckian HUP, for metric tensors, the quantum measures in four dimensions break down. We try to ascertain if a Pre Planckian HUP is sufficient to avoid this pathology and also look at if division algebras which can link Octonionic geometry and E8, to Quark spinors, in the standard model and add sufficient definition to the standard model are necessary and sufficient conditions for a metric tensor HUP which may remove this breakdown of the sum rule in the onset of the “Big Bang”.
Keywords:
Quantum Measures, Spatial Diffeomorphism, Cylinder Sets, Caratheodary-Hahn-Huvanek Theorem, Big Bang Singularity, Causal Sets, Modified Pre Planckian Heisenberg Uncertainty Principle HUP, Division Algebras

1. Introduction
As stated in 2012 [1] , the author came to the conclusion as to the existence of a situation where a Stoica induced “non pathological” singularity would disrupt the existence of a functional quantum measure in 4 dimensions. The relationship of this construction to the Sum rule is explained, Afterwards, we introduce constructions as due to a new Heisenberg Uncertainty principle HUP, as given by [2] [3] [4] which among other things demonstrates the method which can give a start to cosmological expansion of the universe, and we assert that in certain cases, the answer in terms of an energy flux may indeed falsify the conclusion given in [1] . To start off, we consider in this paper whether in the absence of a Heisenberg Uncertainty principle HUP, as given in [2] [3] [4] if singularity behavior in space-time can be affected by co-ordinate choices1. Afterwards, we will examine the role of the Heisenberg uncertainty principle HUP given in [2] [3] [4] and also consider the formulation of the problem needs more than four dimensions, or if it does not. This delineation of the number of dimensions needed to solve the initial problem as given in [1] will be central to determine if the Heisenberg uncertainty principle HUP as given in [2] [3] [4] has any applicability to space-time initial conditions.
2. What If We Neglect the Modification of the Heisenberg Uncertainty Principle HUP as Offered in [2] [3] [4] ―This Segment Is from [1]
In this situation, without considering a modified Heisenberg Uncertainty principle, HUP, in Pre Planckian space, as given by [2] [3] [4] , we digress back to the older situation as given by [1] , i.e. we’re forced then to consider having to have more than four dimensions.
As stated before in [1] we then unequivocally state that the following will hold. From [1] , we have the following quote
Quote:
A proper choice of coordinates is going to involve more than four dimensions and that what is chosen in four-dimensional space-time usually in the Roberson Walker metric will lead to a singularity problem. We claim that this affects the quantum measure problem in four dimensions. The main point of the article is below where we outline how to fix the glaring problems in four-dimensional measures theory which we state as unphysical.
We note here that higher dimensions will, as in String theory, remove this problem. We wish to reconcile the four and higher dimensional examples of co ordinate behavior and reflect upon what the four dimensional representation does to quantum measures, especially if there is a removal of the standard four dimensional representation of a mathematical singularity at the start of inflation. To do this, we will give an argument which will point in the direction of vanishing of disjoint sets in four dimensions leading to a breakup of the quantum measure in four dimensions.
Our initial goal is to show that disjoint sets, are due to separability in a topological sense, and that at a point in space?time, that the very notion of separability breaks down completely [5] .
Separability in a topological sense can be constructed as follows. A topological space X is said to be separable if X has a countable dense subset. In other words, there is a countable subset D of X such that closure (D) = X.
Equivalently, each nonempty open set in X intersects D. The fact is, that if there is a space?time point, that the countable subset D of X is such that the closure (D) = X breaks down completely.
Afterwards, we should note that disjoint sets in a topological space, X, are due to working with X being a Hausdorff space. We then note the properties of Hausdorf spaces can be written follows:
1) If K is a compact subset of X and 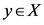 is a point outside of K then y and K have disjoint neighborhoods, i.e. there exist an open neighborhood
is a point outside of K then y and K have disjoint neighborhoods, i.e. there exist an open neighborhood  of y and an open set
of y and an open set 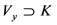 for which
for which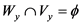 .
.
2) Every compact subset of X is closed.
3) Any two disjoint compact subsets of X have disjoint open neighborhoods, i.e. if C and D are compact disjoint subsets of X, then there exist open sets  and
and 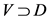 for which
for which .
.
Note that when one has a point in space time, the there is not a comparable construction to closure (D) = X or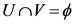 .
.
This lack of having at a point in space-time a topological set X with open subsets with these constructions dooms having these properties. I.e. if one does not have a Hausdorff space, one is going to find it impossible to form disjoint sets in a separable X if X is itself a point.
When one does not have separable sub sets, at a single point, then the construction used for quantum measures breaks down. We review in Appendix A what happens due to Stoic’s treatment [6] of the Friedman and acceleration equations and show it implies a smoothness condition which eliminates disjoint sets at a point, entirely, i.e. no pressure, density and scale factor.
While the existence of the pathological singularity can be treated by use of Planck’s length, which can be used to construct disjoint sets, if Stoica is believable, this Planck’s length is no longer essential, which brings up interesting questions so far avoided by main stream cosmologists. This paper merely brings up that issue, and asks what can be done to correct for it, at the point of the big bang. To do this, we later revisit what happened in Surya’s paper [7] in the DICE 2010 conference, and make a few suggestions of our own afterwards. Appendix A summarizes how Surya built up her quantum measures and is mandatory reading for those wishing to understand how quantum measures are built up outside the point regime so specified by Surya which is claimed to break down in usual singularity regimes at the origin of the big bang2.
Our contribution is to examine quantum measures assuming a non-string theory treatment of cosmology. And to argue that the breakdown of a quantum measure in four dimensions necessitates use of higher dimensional embedding of the start of cosmological inflation.
End of quote of [1] .
This concludes our introduction as to what is done if the Heisenberg Uncertainty principle HUP of [2] [3] [4] [8] [9] is not used to generate a vacuum energy which could change the conclusion as to the necessity of higher dimensions in order to remove the breakdown of the vector measure of the so called quantum vector measure.
What we will do next is to elaborate the HUP which is cited in [2] [3] [4] [8] [9] which given certain conditions will possibly conserve the quantum vector measure.
3. What If We Put in the Construction of [2] [3] [4] and from First Principles, Included in a Revised HUP for Metric Tensors Based on [8] [9] [10] [11] ?
In order to do this we will be looking at the following construction. From [2] [3] [4] [10] [11] we can cite the following
Iliac. Examining what happens in Pre Planckian Space time 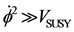 due to
due to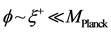 ?
?
We will be looking at the value of Equation (1) if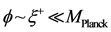 . In short, we have then that
. In short, we have then that
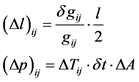 (1)
(1)
If we use the following, from the Roberson-Walker metric [2] [3] [4] [6] .
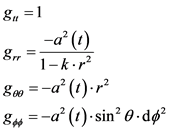 (2)
(2)
Following Unruth [8] [9] , write then, an uncertainty of metric tensor as, with the following inputs
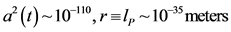 (3)
(3)
Then, if 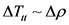 [2] [3] [4] [6]
[2] [3] [4] [6]
 (4)
(4)
This Equation (14) is such that we can extract, up to a point the Heisenberg Uncertainty principle HUP principle for uncertainty in time and energy, with one very large caveat added, namely if we use the fluid approximation of space-time [2] [3] [4] [6]
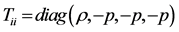 (5)
(5)
Then [2] [3] [4] [6] [8] [9] [10] [11]
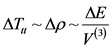 (6)
(6)
Then,
How likely is
We next will then go into a description of what Equation (7) will do to the issue of if not the quantum measure breaks down to that we will work from the stand point of what a traditional quantum measure will do and to put in what the situation is, if we use Equation (7) and if we do NOT assume Equation (7), in terms of a local HUP.
4. Aftermath of Spatial Diffeomorphism Leading to Quantum Measures If Not Using Heisenberg Uncertainty Principle HUP
We use, in part a page and a half of information directly from the initial paper [1] to set up what we will be reviewing as a case of what happens if there is no uncertainty principle to eliminate the presumed singularity.
From [1] we will make use of the following quote of background from the initial starting paper: This is quoting in part of the background from the FIRST reference [1]
As given in [1] Appendix B refers to bi-additivity of D leading to finite additivity of

The use of finite additivity of 
We assert that if Planck’s length is mandatory due to space-time evolution from a HUP as done later, then there is no question that Equation (8) holds. Furthermore, we assert that the 2nd half of this paper due to the HUP does satisfy Equation (8) so the Surya hypothesis as given in [1] holds.
The difference in what we are proposing in the 2nd half of this paper is that unlike the situation from [1] , is that the introduction of quantum HUP, from first principles, as done later, will mean that we will avoid having to use the argument given in [1] as reproduced below in section IV a. below. But what if there is no HUP and that we have a breakdown of a minimum length? i.e. then frankly Equation (8) breaks down. If there IS a HUP, then Equation (8) does NOT break down.
Assuming no HUP, as is done later, we will present reference [1] construction leading to the conclusion of the violation of Equation (8), and why.
Arguments against Equation (8) in the Vicinity/Origin of the Big Bang Singularity If There Exists no HUP, for Space-Time Metrics
If there is a HUP for space-time metrics, then the main problem, of applying Equation (8) lies in insuring the existence of disjoint sets at a point of space-time. If we can get through the HUP, the existence of a minimum space-time length allows us to state, there can be disjoint sets, and then the math construction of Surya [7] goes through verbatim.
We recite the results of [1] in the case that there is NO HUP and that there is NO smallest “length”.
Classical relativity theory though will not allow applying Equation (8). In our 2nd half of the paper will claim that Equation (8) holds. We claim that this is due to the disappearance of the Pathology given in page 5 of Reference [1] .
Now, let us go through what we did in [1] which means that we have to show that there is no way we can have disjoint sets. What are the consequences? In essence, the elimination of disjoint sets destroys a quantum measure. What does this entail and why?
To do this, let us review the notion of a quantum measure.
The precondition for a quantum measure 





We then come to our main result. In the case of NO Heisenberg Uncertainty principle HUP as we talk about later in the 2nd part of the paper, then Equation (8) is replaced by the inequality, i.e. the elimination of disjoint sets will lead to.

Not being able to have a guarantee of having n disjoint sets 

So what do we call the quantum measure generally? In Equation (10) the existence of the quantum measure is defined by the supremum argument.
Now what about the inequality of Equation (9) in the case we eliminate disjoint measures, and how would that lead a change in Equation (8) to Equation (9)?
This is what becomes very problematic if [14] [15] is true about non pathological consequences of a BB singularity, i.e. in the case of no initial singularity the following argument holds.

Our claim is as follows. The Supremum argument as of Equation (10) in the case of NO HUP for metric tensors is no longer valid. If there is no HUP for metric tensors, then the elimination of disjoint partitions means that we have then the elimination of the equality as given in Equation (10).
Why would this break down if we do not apply a metric Heisenberg Uncertainty principle HUP?
We claim that the existence of a singularity will not allow us to analyze disjoint partitions. We furthermore claim that the result we are referencing is that Equation (10) DOES INDEED hold if a metric tensor Heinsenberg Uncertainty principle HUP exists which gives geometric existence to space-time permitting the existence of disjoint sets.
We furthermore claim that if we do not have a metric tensor Heinsenberg Uncertainty principle HUP, that we eliminate disjoint sets. Then we go to Equation (11) below.
If we do NOT apply a HUP which removes the presumed singularity, then Equation (10) is now an inequality written as:

Our point as to what happens if an inequality holds, is due to a breakdown of the notion of “unconditional convergence of the vector measure.”
Equation (10) depends upon having [14] [15] an “unconditional convergence of the vector measure over all partitions”. Replace partitions with causal set structure, and one still has the same requirement of an unconditional convergence of the vector set over all “causal set structure”.
Equation (11) is what we have if no Heisenberg Uncertainty principle HUP exists, and that the main result of our paper is that Equation (11) no longer holds, and that we instead have Equation (10) if a metric tensor Heinsenberg Uncertainty Principle HUP exists. We detail the reasons for that statement in Section V below.
5. Pointing out How Equation (11) Is influenced by the Heisenberg Uncertainty Principle HUP of Equation (7)
In order to reformulate the conclusions of Equation (11), we will be examining if the existence of Equation (7) stops physical disruptions of a disjoint partition, i.e. what we will be examining if we have an effective way to examining disjoint partitions, as showing up for why in the case of not using Equation (7) we had effectively removed the singularity at the beginning of space-time.
5.1. What Would Be Necessary to Remove a Singularity as Given by Stoica? And Hawking’s?
Usually as given by Penrose-Hawking singularity theorems [16] as well as the Penrose theorem [17] we have that there is, initially, a closed trapped surface that was introduced. A closed trapped surface exits, as given by [18] if
Quote
The strategy of the sketched proof presented was to assume that null geodesics were complete, proving that then the boundary of the future of the closed trapped surface is compact.
End of quote.
Strategy here, is to remove the caveat of compactness. Compactness, according to [18] [19] is the situation combining closed, and bounded, and in this situation, it is part and parcel of the classification theorem for compact surfaces which can be accessed in [19] .
We now should go to a new version of the modified HUP, and it will be stated as approximately as that unless an inflaton field exists in the Pre Planckian space-time so that [20]

Then by [2] [3] [4] [10]

Perforce, the enormity of the change in energy, will remove the possibility of a closed surface, in the Pre Planckian space-time, i.e. in doing so, the change in energy disrupts conditions as given in [21] .
We shall next go to the division algebra results and gravitons, to give more structure to applying Equation (13) above.
5.2. What Leads to the Division Algebra Results? i.e. What Happens If There Is a Breakdown of Initial Singularities? Referencing [22] [23]
In [22] , Dixon references [23] where in [22] there is a statement which resonates, i.e. if there is no bounded initial space, and there is a breakdown of compact bounded surfaces, due to what we have with Equation (13), then one has to seriously consider the following quote
Quote:
“Each of the four Division Algebras R, C, H, and O can also be viewed as a spinor space”, and later “The mathematics linking these pairs is an SU (2) group.”
i.e. so what permits the existence of a spinor space in a non-Compact domain? To whit the existence of gravitons, in a non-compact space-time, and we will state then that there are theoretical arguments that a massless spin-2 particle has to be a graviton. The basic idea is that massless particles have to couple to conserved currents, and the only available one is the stress-energy tensor, which is the source for gravity. If a graviton is massless, a given as given by [24] is that there exist 2 polarization states h_ (+) and h_(x), as are given, and that if there are massive gravitons, we will have by [25] that there are additional states. We assert in the case that the mass of a graviton, is about 10^-62 grams, as given in [26] that initially it would be appropriate to look at the two helicity states, in the massless cases as an approximation, i.e. h_(+) and h_(x), and to compare directly with generic SU(2) states, via the following identification. Normally, a spin S object will have 2S+1 polarization states. But for massless particles the transverse modes can’t exist due to Lorentz invariance. Only the positive and negative helicity states remain. So, the graviton will have only 2 helicity states. The SU (2) up and down states, as in the case of the Pauli matrices, can be seen to be simply

We can of course, make a simple identification of h_ (+) and h_(x) with the Up and Down states of Equation (14), due to the fact that in the massless case, there are only 2 helicity states. We could as an example, make a simple relations

As stated by [22] [23] when have that the division algebras, in the quaternion setting may be linked by SU (2) via the methodology for complexification of the Quaternions in [22] , via

According to [22] , R is real, C is complex number, H, is Quaternion, and the O is octonionic
In the case of Equation (16), [22] on page 47 claims that it is a
Quote:
“Complexification of Quaternions’ and is equivalent to a pair of Paul Spinors, and if we form a Column matrix of two such elements we get a pair of Dirac spinors.”
End of quote.
Furthermore from page 47-48 of [22] we have that
Quote:
“It is very interesting that the set of all unit quaternions is a copy of SU(2) (Since H is 4 dimensional, the set of unit quaternions is topologically the same as the set of all points in 4 space a distance 1 from the origin, which is the 3-sphere, one of our Parallelizable spheres).”
End of quote.
This is the language of what [22] calls 1, 3 spinor space-time.
In addition,

Is called in [22] are called a 1, 9 spinor space-time., where [22] states on page 48, that
Quote:
“P and T spinors are SU (2) doublets, so that leaves us with the reduced group, SO (1, 3) X U (1) X SU (2) X SU (3).”
The summary of what we are looking at is [27] , i.e. here on page 284,

Each element of Equation (18) is given by

This refers to 1, 2, 4, and 8 “dimensional” spheres, and 1, 2, 4, 8 are the Caley numbers. This construction should be seen as a way of quantifying, as an example, Equation (18) as a direct construction of 4 SU (2) “spinors, and 2 Quaternion spinors”. The moral being that we can build up a systematic algebra this way, which can use the set of spin ½ wave function eigenvalue entries to build up through Equation (17), Equation (18) and Equation (19) a linkage of 1, 3 spinors as given by a proper interpretation of Equation (16) as with comparison with 1, 9 spheres given in Equation (17), Equation (18) and Equation (19). This construction though, and a linkage to massless versions of the Graviton, works well, if we wish to tie in the usual construction which may be appropriate for the interpretation of the 2 graviton polarization states as having a time in, via Equation (14) and Equation (15) with the UP and Down basis spinors of SU (2) and by extension the buildup of the spinors of the Octonian as alluded to in Equation (18).
The relevance, in terms of space-time, in the case of massless gravitons is as follows, namely that if we can make the identification of Equation (18) and link that to the idea of Equation (15). Then the following situation occurs, namely.
The change in geometry is occurring when we have first a pre quantum space time state, in which, in commutation relations [27] (Crowell, 2005) in the pre Octoionic space time regime no approach to QM commutations is possible as seen by

Equation (20) is such that even if one is in flat Euclidian space, and i= j, then

In the situation when we approach quantum “octonion gravity applicable” geometry, Equation (20) becomes

Equation (22) is such that even if one is in flat Euclidian space, and i= j, then

Also the phase change in gravitational wave data due to a change in the physics and geometry between regions where Equation (21) and Equation (22) hold will be given by a change in phase of GW, which may be measured inside a GW detector.
6. Discussion of the Geometry Alteration Due to the Evolution from Pre Planckian to Planckian Regimes of Space Time―If Equation (15) and Equation (18) Hold
The simplest way to consider what may be involved in alterations of geometry is seen in the fact that in pre octonionic space time regime (which is Pre Planckian), one would have [27] (Crowell, 2005).
This Pre Octonionic space-time behavior should be seen to be separate from the flatness condition as referred to in [27] . But retuning to [27] we have that, in Pre Planckian space-time, that.

Whereas in the octonion gravity space time regime where one would have Equation (22) hold that for enormous temperature increases Equation (22), then by [27] (Crowell, 2005).

Here,

We argue that Equation (24) holds, and that the Stoica non pathological singularity is removed, if there is a sufficiently large energy flux given by change in energy, in Equation (13), but this requires that it not be infinite.
We shall next go to the conclusions and to first review the conclusions made if we do not have the modifications due to an ultra large change in initial energy due to Equation (13).
7. Conclusions, Part A: If We Do Not Use Equation (13)―This Is the Case Where the Stoica Non Pathological Singularity Is Kept
First of all, the question we need to ask is, “Is the existence of a Planck length, as a minimum length mandatory as to space-time?” If it is, the problem of the existence of disjoint intervals is solved, i.e. we need not worry, even if it is 10^-35 meters in length. If this minimum length exists, Equation (8) holds everywhere.
If a mandatory minimum non-zero space-time interval is necessary, then there is nothing which forbids the existence of (8) above. If such an interval does not exist, then (1) breaks down. Furthermore, the space of all infinitely differentiable functions is also separable, and a fundamental sequence is the sequence of all powers of x. This is shown by Taylor Series and Weierstrass Theorem [5] . But having either Weierstrass Theorem or Taylor series at a single point of space-time is a non starter, and also the dodge of using the simplification of a finite dimensional normed space breaks down. No longer at a point, many of the computations can be simplified by the existence of a finite basis, where every vector in the space is a linear combination of some subset of vectors in the basis. One does not have a finite basis in a point of space time [5] .
It should be noted that Connes [13] outlines conditions for non-commutative geometry in space-time for the development of exotic basis which in higher dimensions could restore separable space, i.e. even Hausdorff behavior, as would be necessary for disjoint sets to exist. But such a development would be involving encasing the four dimensional singularity as embedded in a hierarchy of higher dimensional geometric spaces. With 3 dimensional space and time at a singular point, one does not have a Hausdorff metric space X, separatability and without having either of the above, then the construction for a quantum measure, as outlined and developed in the given Appendix A will not work out.
In essence, for making a consistent cosmology, our results argue in favor of a string theory style embedding of the start of inflation and what we have argued so far is indicating how typical four dimensional cosmologies have serious mathematical measure theoretic problems. These quantum measure theoretic problems are unphysical especially in light of the Stoica findings [7] .
8. Conclusions, Part B: If We Do Use Equation (13)―This Is the Case Where the Stoica Non Pathological Singularity Is Removed
We argue in this second case, that then the problems are consistent with regards to the sort of measure theory as advocated by Tao [15] , and that the use of Equation (13) removes the problem cited in [1] .
A general comment should be raised, here, that Reference [28] , that we can have if this is true, alternative gravity theories as a result, as noted by Corda, that this will also entail additional graviton polarization states which are in principle possible in extended theories in gravity. That would affect the sum rule ideas as presented, here. In addition, lattice quantum gravity issues, as noted in [14] should be evaluated or dismissed. The end result of all these procedures is that what is brought up in [29] may impact our choice of ideas as to what is a measure, and in doing so give a different result than what is given in [30] as far as the early universe admissible singularities.
In doing this, note that what is implied in our document, if [28] holds with additional polarization states, added, will give even more structure to our results and lead to further potential invalidation of [30] . Dr. Corda is commended for this insight, as communicated to the author, and it means that, as what is now occurring that additional investigations into [30] with its potential future invalidation of the Hawkings-Ellis singularity theorem structure are necessary. It also lays into the distinct possibility that other objects, purportedly with singularities have a different character from what is usually purported as given in [31] , by Frolov, and Novikov, also are of timely import which was recently brought to the attention of the author by J. Dickau in recent communications.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2017) Reconsidering “Does the Sum Rule Hold at the Big Bang?” with Pre Planckian HUP, and Division Algebras. Journal of High Energy Physics, Gravitation and Cosmology, 3, 539-557. https://doi.org/10.4236/jhepgc.2017.34041
References
- 1. Beckwith, A.W. (2012) Does the Sum Rule Hold at the Big Bang. Prespacetime Journal, 3, 101-102.
- 2. Beckwith, A. (2016) Gedanken Experiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwartz Shield Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian-Penrose Inequality and Initial Kinetic Energy for a Lower Bound to Graviton Mass (Massive Gravity). Journal of High Energy Physics, Gravitation and Cosmology, 2, 106-124. https://doi.org/10.4236/jhepgc.2016.21012
- 3. Beckwith, A. (2016) Non Linear Electrodynamics Contributing to a Minimum Vacuum Energy (“Cosmological Constant”) Allowed in Early Universe Cosmology. Journal of High Energy Physics, Gravitation and Cosmology, 2, 25-32. https://doi.org/10.4236/jhepgc.2016.21003
- 4. Beckwith, A. (2016) Gedanken Experiment for Degree of Flatness, or Lack of, in Early Universe Conditions. Journal of High Energy Physics, Gravitation and Cosmology, 2, 57-65. https://doi.org/10.4236/jhepgc.2016.21006
- 5. Engelking, R. (1989) General Topology. 2nd Edition, Sigma Series in Pure Mathematics, 6 Heldermann Verlag, Berlin.
- 6. Stoica, C. (2012) Big Bang Singularity in the Friedman-Lemantre-Roberson-Walker Spacetime. International Journal of Theoretical Physics, 2015, 1-10.
- 7. Surya, Su. (2011) In Search of a Covariant Quantum Measure. http://iopscience.iop.org/1742-6596/306/1/012018
- 8. Beckwith, A. (2016) Gedanken Experiment Examining How Kinetic Energy Would Dominate Potential Energy, in Pre-Planckian Space-Time Physics, and Allow Us to Avoid the BICEP 2 Mistake. Journal of High Energy Physics, Gravitation and Cosmology, 2, 75-82. https://doi.org/10.4236/jhepgc.2016.21008
- 9. Rovelli, C. (1993) A Generally Covariant Quantum Field Theory and a Prediction on Quantum Measurement of Geometry. Nuclear Physics B, 405, 797-815.
- 10. Unruh, W.G. (1986) Why Study Quantum Theory? Canadian Journal of Physics, 64, 128-130. https://doi.org/10.1139/p86-019
- 11. Unruh, W.G. (1986) Erratum: Why Study Quantum Gravity? Canadian Journal of Physics, 64, 1453. https://doi.org/10.1139/p86-257
- 12. Hamos, P. (1943) Measure Theory. Graduate Texts in Mathematics, 18, Springer Verlag, Heidelberg.
- 13. Connes, A. (2000) A Short Survey of Non Commutative Geometry. https://arxiv.org/pdf/hep-th/0003006.pdf
- 14. Loll, R. (1997) On the Diffeomorphism-Commutators of Lattice Quantum Gravity. http://arxiv.org/pdf/gr-qc/9708025.pdf
- 15. Tao, T. (2011) An Introduction to Measure Theory. http://terrytao.files.wordpress.com/2011/01/measure-book1.pdf
- 16. Hawking, S. and Penrose, R. (1996) The Nature of Space and Time. Princeton University Press, Princeton.
- 17. José, M., Senovilla, M. and David, G. (2014) The 1965 Penrose Singularity Theorem. http://arxiv.org/abs/1410.5226
- 18. Senovilla, J.M.M. (2015) The 1965 Penrose Singularity Theorem. http://arxiv.org/pdf/1410.5226v2.pdf
- 19. Gallier, J. (2012) A Guide to the Classification Theorem for Compact Surfaces. http://www.cis.upenn.edu/~jean/surfclass-n.pdf
- 20. Giovannini, M. (2008) A Primer on the Physics, of the Microwave Background. World Scientific, Pte. Ltd, Singapore. https://doi.org/10.1142/6730
- 21. Hawking, S. and Ellis, G.F.R. (1973) The Large Scale Structure of Space-Time. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511524646
- 22. Dixon, G. (2011) Division Algebras, Lattices, Physics Windmill Tilting. G. Dixon, Private Publishers, Chicago, Illinois.
- 23. Dixon, G. (1994) Division Algebras: Octonions, Quaternions, Complex Numbers, and the Algebraic Design of Physics. Springer Verlag, Heidelberg. https://doi.org/10.1007/978-1-4757-2315-1
- 24. Maggiorie, M. (2008) Gravitational Waves, Volume 1, Theory and Experiments. Oxford University Press, New York.
- 25. de Paula, W.L.S., et al. (2004) Polarization States of Gravitational Waves with a Massive Graviton. http://arxiv.org/abs/gr-qc/0409041v1
- 26. Alfred, S.G., et al. (2010) Photon and Graviton Mass Limits, Reviews of Modern Physics, 82, 939-979. http://arxiv.org/abs/0809.1003 https://doi.org/10.1103/RevModPhys.82.939
- 27. Crowell, L. (2005) Quantum Fluctuations of Spacetime. World Press Scientific, Singapore. https://doi.org/10.1142/5952
- 28. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282. https://arxiv.org/abs/0905.2502 https://doi.org/10.1142/S0218271809015904
- 29. Stoica, C. (2012) Beyond the FRWL Big Bang Singularity. http://arxiv.org/pdf/1203.1819.pdf
- 30. Hawkings, S.W. and Ellis, G.F.R. (1973) The Large Scale Structure of Space-Time. Cambridge Monographs on Mathematical Physics, Cambridge. https://doi.org/10.1017/CBO9780511524646
- 31. Frolov, V. and Novikov, I. (1998) Black Hole Physics, Basic Concepts and New Developments. Springer Verlag, Heidelberg. https://doi.org/10.1007/978-94-011-5139-9
Appendix A
This is straight from reference [1] and is applied only if we do not apply Equation (13). Upon application of Equation (13), this application is no longer used, and [6] is not pertinent. And [14] as an elaboration is not considered.
If Equation (13) is not used, which removes, this construction, we state that Stoica [6] does a re-scaling of the pressure and density along t he following lines, namely the initial Friedman equation is changed i.e. it starts with

Furthermore we also have the accelleration equation given by

Using the re-scaling of [6] using 

We then re-scale the density and also the pressure as follows:

This will lead to

The upshot is, as explained in [2] that then;

So then the acceleration equation and Friedman equation vanish at
Appendix B
This is straight from reference [1] and is applied only if we do not apply Equation (13). Upon application of Equation (13), this application is no longer used, and [6] is not pertinent. Also, we then would, if we apply Equation (13) NOT use the additional details in [14] . With that, let us commence the review.
We introduce the formalism by appealing to the concept of spatial diffeomorphism [12] as a necessary condition for linking the physics of what happens at a singularity to outside of the singularity of inflation generated space time geometry. Trivially, a diffeomorphism involves an infinitely differentiable, one-to-one mapping of the model to itself. In contrast, there is a breakdown of differentiability at the start of the big bang, based on non-loop-quantum-gravity theories.
We submit that the difficulties in terms of consistency of Equation (8) of this document. In terms of initial causal structural breakdown-which we claim leads to Equation (8) being re written as an inequality-one has to come up with a different way to embed quantum measures within a superstructure, as noted in the conclusions of this paper. Spatial diffiomorphisms as stated in [12] do not work unless there is a lattice structure, effectively doing away with a singularity. If the lattice structure is not used, differentiability breaks down and one does not have one-to-one mapping of the physics of the big bang singularity onto the rest of the inflationary process. We submit that this breakdown would then make Equation (b1) not definable. As to the measure set structure, the readers are referred to [12] to get the foundations of the measure theory structure understood. The rest of this text is an adoptation of what was done in [6] , with the author’s re interpretation of what the significance is of quantum measures as stated in [6] , in the vicinity of a singularity.
The author’s main point is that there is a breakdown of measurable structure, starting with definitions given in [6] and [12] where the concept of disjoint sets becomes meaningless in a point of space. In the causal set approach, the probabilities are held to be Markovian [6] , label-independent and adhere to Bell’s inequality. The author of [6] refers to a sequential growth called a classical transition percolation model. Then reference [6] extends the classical transition percolation model to complex models involving quantum measures in the definition of a (quantum) complex percolation model. Reference [6] defines the amplitude of transition as follows. For a quantum measure space defined as triple as given by



Let 











This is done for a cylinder set , where 










This probability would be a quantum probability which would not obey the classical rule of Kolmogrov [6]

The actual probability used would have to take into account quantum interference. That is due to Equation (1b) and Kolmogrov probability no longer applying, leading to

Here, 


A quantum vector measurment is defined via

Where





Also 


with a Hilbert space 



So then the following happens,



This is for all 




The claim associated with Equation (b1) above is that since 

The main point of the formalism for Equation (b13) is of bi-additivity of D leading to the finite addivity of

NOTES
1As noted by one of the Reviewers: “one can indeed look at the induced metric at light-cone boundary. It is just r_M^2dOmega^2. There is nothing pathological in its topology nor in the topology of future light-cone when seems as parts of Minkowski space, perfectly well defined but metrically 2-D since radial direction gives no contribution as a light-like direction. This example suggests that one should be extremely cautious in considerations related to singularity: so much depends on a choice of proper coordinates. In fact, holography suggests that one should consider light-cone boundary or initial singularity as sub-manifold of space-time.”
2The Reviewer noted that “In Einstein’s equations for RW cosmology of course rho, p, and scale factor a are scalar invariants which become infinite at the initial moment. This is a real physical singularity. In cosmic string dominated primordial cosmology however the mass per comoving volume vanishes at the singularity like a so that in this sense everything is non-singular. As mentioned Stoica shows that the equations can be redefined to get well-defined equations also at the singularity.”



