Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.04(2016), Article ID:69969,10 pages
10.4236/jhepgc.2016.24038
Linkage of Classical Mechanical (CM) Geometry (3 Dimensional) and Quantum Mechanical (QM) Geometry (2 Dimensional) via Hopf Mapping and Its Implications for Relic Gravitational Wave (GW) Power Production
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 14, 2016; Accepted: August 20, 2016; Published: August 23, 2016
ABSTRACT
Hopf mapping from 2 dimensions Quantum Mechanics (QM) to 3 dimensions Classical Mechanics (CM) is examined in terms of a formalism started by Feynman which has linkage to the (CM) equations of motion have linkage to the Serret-Frenet form (for differential equations). We argue that in doing so we may then link QM representations of qubits to a solved version of the rotating rod problem. Furthermore since a “generic” solid body rotation equivalent to the rotating rod problem has linkage to Gravitational Wave (GW) generation, as given by Lightman et al., it is a way to tie qubits (quantum information) to GW generation. We then make observations as to what the results mean in terms of QM initial states and the power of GW production from early universe conditions.
Keywords:
Hoft Mapping, Quantum Systems, Classical Systems, Gravitational Radiation

1. Introduction
We examine the results of the Hopf mapping from 2 dimensions, quantum mechanics (QM) to 3 dimensions using Classical Mechanics (CM) in terms of generalizations to a rigid rod rotation [1] which could generate GW (gravitational waves). This paper was initiated by a question by Stephen Kauffman about black holes. i.e. the reality of black hole singularities. To this end, this formalism was chosen to be the basis of finding a solution to trying to investigate black hole physics. What we are addressing is a problem created by the following confusion in physics. Namely that decoherence theorists are firm in their assertion that the decoherence of the wavefunction (of the universe?) is automatic based on the fact that nature is measuring itself all the time. This paper addresses that problematic assumption by giving a counter poise to necessary conditions to decoherence of an initial wavefunction of the universe, by specific requirements for initial two-level QM system analysis is prior to generation of GW in the electroweak era of cosmology. Afterwards, we may be able to give a succinct answer to if qubits of information [1] are thereby created in the prior to GW generation era. Note that this transferal from 2 dimensions to 3 dimensions is in reality the holographic principle and its aftermath, with what is very similar to a shock wave in the time of the event horizon [2] . After this formalism is further developed, we will use the two to the three sphere mapping to ask if singularities have a presence in astrophysical problems. To start developing mathematics relevant to that future development, we solve on our own a set of equations (in 3 dimensions) pertinent to a non-symmetric object in rotation in early universe which is a way to generate GW and from there state some caveats as to the power of GW which may ensue. The final conclusion of our document is in linking a quantum quibit form with the power created by/during GW generation which conceivably could be identified by a suitably designed detector. The document first examines what Feynman did with respect to 2 level QM systems, their generalization to classical rigid rod rotation, and then we solve the resulting CM equation of motion. Feynman decomposed the solutions in x, y, and z in terms of the 2 level QM system [3] [4] a decomposition which we hold as still relevant and valid, and then, using the case of a uniform magnetic field “down” the z axis, as a driver to the physical process leading to non-symmetric rigid body rotation. That the body is non-symmetric which allows us to approximate the GW power generated as to the conventions outlined by Lightman, Press, Price, and Teukolsky [5] . We then conclude with a description of what our model says about QM generation of states relevant to GWs in the early universe. In doing so, we are using [6] as a template for information on the interaction of gravitons/ gravitational waves, with the spinning rod, and its connections with classical motions. i.e. Gravitational waves are seen to be connected with a classical formulation and we then connect that with the Feynman description of linkage of classical mechanics to the quantum system, via the documentation provided for in this paper.
2. Outlining the Feynman Development of a Classical Mechanics (CM) System from 2 Level Quantum Mechanics (QM) System
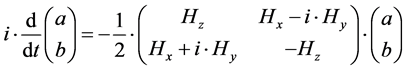 (1)
(1)
In doing so via the transformation
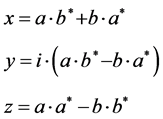 (2)
(2)
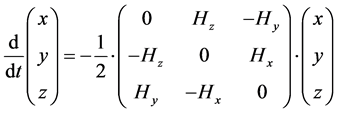 (3)
(3)
The simplest decomposition of this problem is to set  so then the situation is that we have
so then the situation is that we have
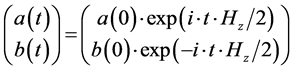 (4)
(4)
And
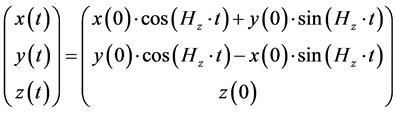 (5)
(5)
As can be seen by Maggorie [5] and also Lightman, Press, Price, and Teukolsky [4] since the solution as given by Equation (5) is for a circular moment of a GW there would be a GW associated with it, We also will be looking at a more complex three dimensional example of motion which is highly complex Non-withstanding we go to a more complete version of Equation (1) to Equation (3) with only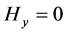 . Then we get
. Then we get
 (6)
(6)
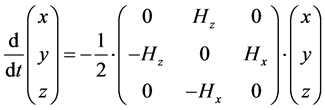 (7)
(7)
The above two equations have the setting of what is called the Serret-Frenet form and we will solve these two DE equation systems taking the approximation that ,
, 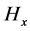 are constants in lieu of the first example. The next section solves these two equations with this in mind, leading to a non-symmetric rotation in 3 dimensional space which is needed for GW production.
are constants in lieu of the first example. The next section solves these two equations with this in mind, leading to a non-symmetric rotation in 3 dimensional space which is needed for GW production.
3. Solving a Simplified Version of Equation (6) and Equation (7) to Come up with a Non-Symmetric Rigid Body Rotation Sufficient to Obtain Gravitational Waves (GW)
To do this we look at Equation (7) in such a way as to have
 (8)
(8)
To which we add in the reconciliation of the variables equation result from the last part of Equation (8), namely
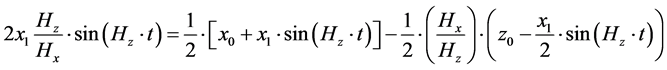 (9)
(9)
Leading to
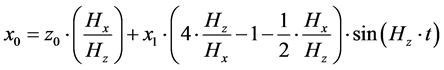 (10)
(10)
Leading to
 (11)
(11)
Combined once again with Equation (2), and assuming that the quantity we roughly identify with the “magnetic field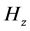 ” is parallel to the z axis, so long as
” is parallel to the z axis, so long as 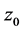 as an initial starting point for the z axis is non-zero, then we have fulfilled the requirement for a non-uniform motion of a “rigid body” which if related to the quantities in Equation (2) and also Maggiore’s criteria for GW from a non-uniform non spherical generation of GW leads to the final part of the GW requirement of non-spherically symmetric motion which lends itself to GW generation. We will then make a comment as to how to link this to GW power using [3] to show how frequency from this example can lead to GW generation.
as an initial starting point for the z axis is non-zero, then we have fulfilled the requirement for a non-uniform motion of a “rigid body” which if related to the quantities in Equation (2) and also Maggiore’s criteria for GW from a non-uniform non spherical generation of GW leads to the final part of the GW requirement of non-spherically symmetric motion which lends itself to GW generation. We will then make a comment as to how to link this to GW power using [3] to show how frequency from this example can lead to GW generation.
4. Conditions Permitting Gravitational Wave (GW)-Power Production Using the Inputs from Equation (5)
The idea is that we need to calculate the following, i.e. a moment of inertia for a system, and also the frequency. As to Equation (5) according to the following, we can come up with a generic Equation of motion, namely if we do averaging and set out a general time averaging. Fortunately for us the trig identities naturally vanish.
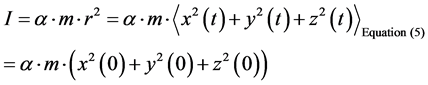 (12)
(12)
We can, as an approximation use m above to be the net mass of the assumed geome-
try and set. 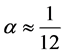
Then we look at the power loss according to a “rigid rod” construction for GW power generation [4] [5] i.e.
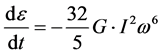
Note that we can approximate the frequency in this case as directly proportional to the input frequency of the magnetic field parallel to the z axis, i.e. looking to first approximation at 
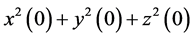

Next we will look at what happens if we assume the input geometry as given by Equation (11).
Both of these results will be then compared to as to the simple case of Equation (4) as due to the first set of inputs into Equation (13) if the spatial geometry of Equation (5) is used, and then Equation (4) will be guessed at if we use the geometry of Equation (11). i.e. we will guess what Equation (11) does to Equation (4) and compare that with what Equation (11) does to Equation (4).
5. Conditions Permitting Gravitational Wave (GW) Power Production Using the Inputs from Equation (11)
This is a mess. i.e. what we have to do is to look at how to calculate the moment of inertia, and then going to Equation (13), even if we assume the same mass which was used earlier to calculate Equation (14) above for relic conditions. To start this, look at,
even if
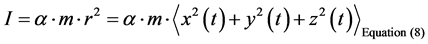
The problem starts immediately, in that the parenthesis of Equation (15) above would have to be a time averaged quantity. i.e. we would be looking at 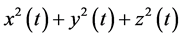
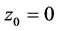
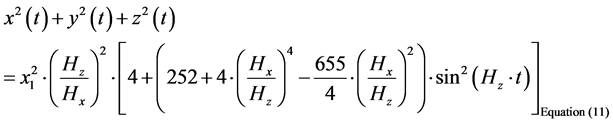
The term to be time averaged would be
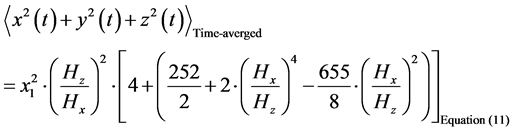
Using a ratio, as given of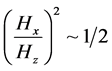
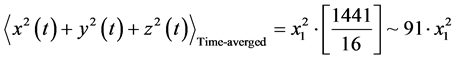
Then the magnitude of the GW power would be, per second about 10,000 times bigger.
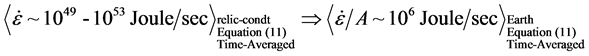
6. Comparison of Equation (14) and Equation (19) Results in Terms upon Solving Equation (1)
The value for the simple geometry (in terms of simple quidbits ) to understand working with both Equation (1) and then Equation (4) has, if a particle is in a constant magnetic field, then according to [4] it is a special case of working with qubits, according to [1] ,
[5] , the values of 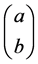

simple. The problem of solving for the functions of an applied non zero 
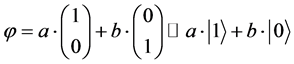
is much simpler than when 
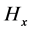
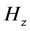
tion, but due to the “noisy” values for a and b, then 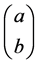
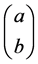
dimensional CM results. Still the same rotating rigid body problem approximated by a rod in spatial rotation, but the movements and more would become much more com-
plicated. And then we find that 
7. Conclusion. Classical Mechanics (CM) and Quantum Mechanics (QM) Correspondence Remains, but Turbulence, a.k.a. Duerrer and Beckwith Results for Early Universe Gravitational Wave (GW) Generation Makes the QM Connection Very Hard to Mathematically Identify. Simple Logical Process, MESSY Algebra Ahead. With a Possible Answer to the Question If Singularities Are Essential in Cosmology
Looking at Equation (13), simpler and harder case, still in the case of relic gravitational wave (GW) production has large number correspondence and scaling as mentioned by Valev [7] , with his H, not a Hamiltonian, but instead
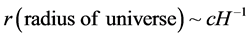
Also, the mass of the Universe, as given by Valev [7] is
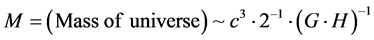
There is here, a template for innate simplicity which can be based, also on keeping in mind the holographic principle, i.e. the QM is embedded and done first with a transferal to CM with the event horizon being the boundary for a phase transition between regimes of space-time, with some of the processes as outlined in [2] . When this is brought up, we should keep in mind that the qubits generated in BHs have their counterpart in early universe cosmology as stated in [8] which shows that event horizon and entropy generation of black holes has a similar analogy to early universe cosmology before the Electro-Weak era. Also there is, when we look at physics innate simplicity in the inter relationship, of the sort mentioned by Valev [7] , in terms of space-time geometry. The inter relationship of CM and QM given by Equation (1) and then Equation (3) with the stunning interplay between x, y, z and a, b given by Equation (2) is, we believe, ob-
scured by how complex the problem is of finding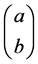
between the qubits given in Equation (20) and the complex systems given in Equation (20) and the inputs into Equation (2). This interrelationship depends upon the complex systems as given by Equation (11), for Classical mechanics or Equation (5) as seen in references [9] [10] . Finally the author suggests that the linkage of three sphere topology involving classical mechanics (CM) to two sphere topology involving quantum mechanics (QM) is a very useful starting point to answer an objection by Dr. Kauffmann to the existence of singularities in General Relativity, as well as the classical GR treatment of black holes. As related by Dr. Kauffmann, quantum mechanics routinely prunes out non-physical solutions with regard to the hydrogen atom and only uses solutions which are physically feasible. Dr. Kauffmann asserts no such pruning of solutions occurs in black hole physics or in the formation of cosmological singularities. The author in [10] used chaotic space-time conditions for generating GW in the electro- weak era. Furthermore, the author asserts that turbulence as exemplified by [9] is the driver of relic GW generation and GW power calculations. If so, further development of the Hopf mapping results from 2 dimensions (QM) to 3 dimensions (CM) may
enable us to identify necessary conditions for finding 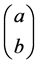
sary for relic GW development. It is well known that spherically symmetric geometry
will generally not generate GW. This puts a restriction upon finding 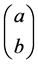
turn would answer if an initial space-time singularity is even feasible. Note also that
necessary conditions of how to construct and finding inputs into 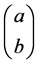
avoid a serious logical error by many physicists. This error is due to confusion about how to form an initial wave-function of the universe. Namely as stated initially by the author, that decoherence theorists are firm in their assertion that the decoherence of the wave-function (of the universe?) is automatic, based on the fact that nature is measuring itself all of the time. This paper addresses that problematic assumption by giving a counter poise for necessary conditions to the decoherence of an initial wave-function of the universe, by specific requirements for forming an initial two level QM system for analysis is prior to the generation of GW in the electro-weak era of cosmology, also in finding sufficient conditions for an adequate input into the initial wave-function
called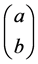
different mechanisms [11] [12] purport to have solutions to the initial cosmological state that the author views development of mandadatory restrictions upon acceptable
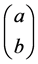
vestigating rigorously the question if singularities are indeed necessary and even allowed in astrophysical problems. Qubit analysis of the two-level QM state created by
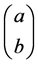
Borsten, Duff and Levay [13] give a plan of action statement as to how to tie in qubits into entropy of Black holes. But in doing so there is a serious confusion relating to the fact that specific information about black holes, and also the universe is purely abstract unless a conscious observer or their measurement apparatus is there to observe and cognize it. If this is true for qubits relating to black holes, it is also even more true for the assumed singularity at the start of the initial configuration of the universe. As given by Muller, and Lousto [8] there is a way to give very similar treatment of entanglement entropy for both black holes and the initial universe. Then, the way qubits are measured and used will allow us to ask what entropy and information are stored in what is commonly purported to be a singularity. If it is one (a singularity), which will be the final question to answer. The author also has an accepted publication in the Journal of Applied mathematics, on this very question [14] with the answer that this question is not open and shut. i.e. that further work needs to be done in this area. This present Hopf mapping from Quantum Mechanics (QM) to classical mechanics (CM) with, as argued here, CM turbulence generating GW, may be a way to determine restrictions upon initial states in QM which the author views, as a way to answer Dr. Kauffmann’s question in a rigorous role in the near future. Qubit analysis, if stated appropriately along a simplified version of [12] while keeping in mind [13] and the cautionary example in [14] will either confirm or disavow the existences of cosmological singularities. Namely we need to know and confirm if qubit presentation of black hole and early universe information leading to entropy (which may lead to gravitational wave (GW) generation [10] ), is commensurate with either singularities in space-time or their explicit disproval of existence, if that is possible.
We should mention in passing that [15] must be satisfied as far as initial conditions, i.e. the Hopf mapping with its linkage of classical to quantum mechanics may allow for an investigation of the accuracy of the Post Newtonian approximation which was used, initially in the start of data analysis of the results of [15] . Furthermore it is to be hoped that what Dr. Corda brought up in [16] , i.e. “accurate angular and frequency dependent response functions of interferometers for GWs arising from various Theories of Gravity”, will permit distinguishing between either General Relativity, or Tensor-Scalar models of gravity for gravitational generation. If the mechanism of this paper is shown to be relevant to experimental General Relativity, or a competitor to General Relativity as far as the presumed scalar-tensor models of gravity, we will be hopefully making progress as to the formation of gravitational wave astronomy, from the early universe.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2016) Linkage of Classical Mechanical (CM) Geometry (3 Dimensional) and Quantum Mechanical (QM) Geometry (2 Dimensional) via Hopf Mapping and Its Implications for Relic Gravitational Wave (GW) Power Production. Journal of High Energy Physics, Gravitation and Cosmology, 2, 447-456. http://dx.doi.org/10.4236/jhepgc.2016.24038
References
- 1. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
http://arxiv.org/abs/0905.2502
http://dx.doi.org/10.1142/s0218271809015904 - 2. Abbott, B.P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, 061102.
https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102
http://dx.doi.org/10.1103/PhysRevLett.116.061102 - 3. Beckwith, A. (2013).
http://vixra.org/abs/1304.0156 (Accepted for Publication in Journal for Applied Mathematics, SCIRP) - 4. Borsten, G.L., Duff, M. and Levay, P. (2012) The Black Hole/Qubit Correspondence: An Up-to-Date Review. Classical and Quantum Gravity, 29, 224008.
http://dx.doi.org/10.1088/0264-9381/29/22/224008 - 5. Ellis, G., Maartens, R. and Mac Callum, M. (2012) Relativistic Cosmology. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139014403
- 6. Padmanabhan, T. (2010) Gravitation, Foundations and Frontiers. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511807787
- 7. Beckwith, A. (2015) How Graviton Power Values and a Graviton Count from the Electroweak Era, Give Strain and Heavy Gravity Values. In: Dumarchez, J., Fontaine, G., Klima, B. and Van, J.T.T., Eds., The Inaugural Confrence on ICISE “Windows to the Universe” under the Patronage of “Annee France-Vietnam 2013-2014” under the High Patronage of UNESCO, The Gioi Publishers, Hanoi, 411-412.
http://vixra.org/abs/1308.0110 - 8. Durrer, R. (2009) Massimiliano Rinaldi. Physical Review D, 79, 063507.
http://arxiv.org/abs/0901.0650
http://dx.doi.org/10.1103/PhysRevD.79.063507 - 9. Muller, R. and Lousto, C. (1995) Entanglement Entropy in Curved Spacetimes with Event Horizons. Physical Review D, 52, 4512-4517. arXIV: Gr-qc/9504049v1
- 10. Valev, D. (2014) Estimation of the Total Mass and Energy of the Universe. Physics International, 5, 15-20. http://arxiv.org/pdf/1004.1035.pdf
- 11. Maggiore, M. (2008) Gravitational Waves, Volume 1: Theory and Experiment. Oxford University Press, Oxford.
- 12. Lightman, A., Press, W., Price, R. and Teukolsky, S. (1979) Problem Book in Relativity and Gravitation. Princeton University Press, Princeton.
- 13. Feynman, R. (1966) The Feynman Lectures on Physics. Vol. 3, Adsdison-Wesley, Reading.
- 14. Feynman, R., Verno, F. and Hellwarth, R. (1957) Geometrical Representation of the Schrodinger Equation for Solving Master Equation. Journal of Applied Physics, 28, 49-52.
http://dx.doi.org/10.1063/1.1722572 - 15. Darabi, F. and Jalalzadeh, S. (2013) Cosmological Quantum Tunneling and the Holographic Principle. Theoretical and Mathematical Physics, 175, 710-716; Also See Much the Same Thing in http://arxiv.org/abs/1108.0682
http://dx.doi.org/10.1007/s11232-013-0056-7 - 16. Kholodenko, A.L. (2013) Applications of Contact Geometry and Topology in Physics. World Scientific.
http://dx.doi.org/10.1142/8514