Received 12 April 2016; accepted 17 June 2016; published 20 June 2016

ABSTRACT

Haggard and Rovelli delineated an outer radius as to the range of quantum effects, which extends past the Schwartzshield radius. This is defined as 7/3 times the mass of the initial cosmological system. We also have a range of perturbative effects as delineated by Turok’s article which gives a range of values of 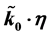for which second order perturbative terms in cosmological evolution may play a role, where we have second order perturbation terms for which. Right afterwards, there are no perturbative behavior and no perturbation if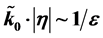. This is the 2^nd order term for perturbing term for GW (Gravitational wave) as denoted by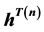, and near the “zero point” of cosmological expansion, and from there we determine the size of the quantum effects, i.e. when they initiate, the relevant initial entropy, so as to determine the radii of initial cosmology, so quantum gravity may initiate its activity, in our toy universe. The criteria of Turok is used to obtain the relevant mass, m, used in the initial radii so that it is 7/3 times the mass of the initial cosmological system. We use the “Criteria of Turok” to delineate the start of quantum gravity effects. Mass m is done via appealing to graviton mass, and that times initial entropy, which is commented upon in Equation (9).

Keywords:

Quantum Effects, Haggard and Rovelli

1. Introduction

We start with what Turok [1] wrote up as to the initial starting point of analysis, as to where he described the cosmological evolution to describe a perfect bounce, “in which the universe passes smoothly through the initial singularity”. A perfect bounce is a way to describe an interference free, simple matter-energy transition from a prior universe to the present universe. What we analyze for our purposes, is the 2nd order perturbative term of hT(n). We find that for cosmological perturbations, the cosmological perturbations have a 2nd order contribution. We set this 2nd order contribution as follows:

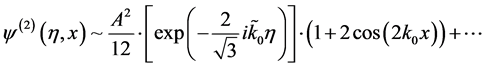(1)

which is a 2^nd order perturbative term for the equation for the evolution of h, if 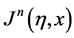is nonlinear

(2)

Then setting a conformal time as approaching early universe conditions requires that

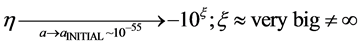(3)

Our supposition is, then that we have the following for well-behaved GW (gravitational waves) and early cosmological perturbations being viable, in the face of cosmological evolution with modifying the formalism of Turok [1] to obtain

(4)

In practical terms near the initial expansion point it would mean that near the beginning of cosmological expansion we would have an initial energy density of the order of

(5)

If so then, if we assume that gravitons have an initial (at about the start of inflation) rest mass of about 10⁻⁶² grams, and that Planck mass is about 10⁻⁵ grams, if gravitons were the only “information” passed into a new universe, making use of the following expression for the initiation of quantum effects, i.e. by Haggard and Rovelli [2] of

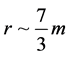(6)

We should reflect upon what Equation (6) is saying. It is stating that quantum effects, in the early universe are proportional to mass, and below, we are bringing up what the particulars of the quantum effect inducing mass should be.

Then, we would have, the initiation of quantum effects as of about [2]

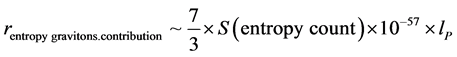(7)

Then by making use of Equation (5) we could, by dimensional analysis, start the comparison by setting values from Equation (4) and Equation (7) to obtain.

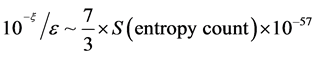(8)

So that to first order, a graviton count, for a radii of about the order of 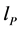(Planck length at the start of inflation is, approximately 1.6 times 10⁻³³ centimeters) would be if we take the entropy as dimensionally scaled by the expression given in Equation (9).

(9)

Depending upon what we use from the values given in Equation (5) above, as well as the values given by, we then obtain Equation (9). The information as given in Equation (9) is closely in correspondence with Equation (7) above. We hope then that Equation (1) vanishes, i.e. the wave function, so then this vanishing of Equation (1) is the subsequent topic of the next topic we raise in our manuscript. This will then lead to a condition for which Equation (1) vanishes, which is the next chapter to consider.

2. Considerations of What Could Lead to Equation (1), I.E. 2^nd Order Perturbation to Cosmological Evolution, Vanishing

The simple short course as to the radius achieving its starting point to being quantum mechanical in its effects, from the big bang initiating from a quantum bounce is to have the following threshold for quantum effects to be in action, to the vanishing of Equation (1). Here the quantum effects start with a value of

(10)

Note that the term, l with subcript p is for the Planck Length. Equation (10) is indicating that the quantum effects start at the beginning of cosmological expansion.

If Equation (1) is zero due to and we want Equation (1) to vanish, it leads to the following for the vanishing of the 2^nd order perturbative effect, with the critical value of wavelength for which Equation (1) vanishes, i.e. hence, borrowing from the spin offs of [1]

(11)

It means that there is the following interval may be our best Quantum Mechanical perturbative indicator in terms of Equation (1), that is

(12)

3. Comparing the Variance in Position Given in Equation (12) with Modified HUP

Note this very small value of spatial variable x comes from a scale factor, if we use a very large red shift [3] [4] , i.e. 55 orders of magnitude smaller than what would normally consider, but here note that the scale factor is not zero, so we do not have a space-time singularity [3] [4] . The scale factor is 1 in the present era, so this tiny scale factor as given by, is at the onset of cosmological expansion.

Then

(13)

We will next discuss the implications of this point in the next section, of a nonzero smallest scale factor.

We will be using the approximation given by Unruh [5] , of a generalization we will write as

(14)

If we use the following, from the Roberson-Walker metric [3] [4] .

(15)

Following Unruh [5] , write then, an uncertainty of metric tensor as, with the following inputs

(16)

Then, the surviving version of Equation (7) and Equation (8) is, then, if [3] [4]

(17)

4. Conclusion. Equation (17) May, with Refinements of R = X, in the Four Dimensional Volume Delineate the New HUP, in Our Problem

If from Giovannini [6] we can write

(18)

Refining the inputs from Equation (18) means more study as to the possibility of a nonzero minimum scale factor, as well as the nature of an inflation like scalar field of as specified by Giovannini [6] . Then we will assert that if r = x then if we use

and then the volume, as used in [3] [5]

(19)

This Equation (19) will be put into, if, it means that

that this is defined for all x as to where and when

holds, with the lower value for x signifying the spatial range of x for which quantum mechanics is valid, with three times that value connected as to when the perturbative methods break down. Thereby influencing the range

of values for in. Furthermore we have, if there is an eventual weak field ap-

proximation according to Katti [7] gravitational spin off according to, with a gravitational wave signal according to, if [3] [4] .

(20)

If the contribution from Pre Planckian to Planckian is due to the stress energy tensor as given in form [3] [4] , it means that the relevant relic GW signal will be of the form, with a small quadrupole tensor.

(21)

The m here is the mass of a graviton, times the relic entropy. Here in picking relic entropy we are approximating entropy as a strict numerical counting of “particles”. The entropy is given by Equation (9) with an estimated magnitude of about 10²⁰ to at most a peak value of 10³⁶. This Equation (21), plus its consequences will be examined later on, while we assume, r is the radial distance variable.

We wish to investigate generalizing the initial conditions as given in reference [8] . Changing of these initial conditions may change the fluctuations we cite in the form of Equation (21). Alteration of the initial conditions may lead to further refinement of the Turok criteria we have worked with in the formulation of our paper's research assumptions. Further care must be taken to keep whatever initial conditions and our choice of inputs into Equation (21) as being in fidelity with [9] experimental considerations of relativity and cosmology. While also reviewing [10] . In addition, it is important to note that fine tuning of Equation (21) has to take into consideration inputs from [11] as to the epoch making discovery of gravitational waves, by LIGO, for experimental veracity, and that also, the input from Equation (21), if suitably dealt with would be vital for the purpose of determination of if scalar-tensor gravity, or General Relativity is the definitive theory of gravity. Dr. Corda’s work in [12] will be vital in terms of determination of the significance of both Equation (20) and Equation (21) and a thorough understanding of Equation (21) and Equation (20) may enable fuller comprehension of [4] to foundational cosmology and particle astrophysics.

Acknowledgements

This work is supported in part by National Nature Science Foundation of China grant No. 11375279.

Cite this paper

Andrew Walcott Beckwith, (2016) Gedanken Experiment for Delineating the Regime for the Start of Quantum Effects, and Their End, Using Turok’s Perfect Bounce Criteria and Radii of a Bounce Maintaining Quantum Effects, as Delineated by Haggard and Rovelli. Journal of High Energy Physics, Gravitation and Cosmology,02,287-292. doi: 10.4236/jhepgc.2016.23024

References