Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.01(2016), Article ID:62208,18 pages
10.4236/jhepgc.2016.21001
5D World-Universe Model. Neutrinos. The World
Vladimir S. Netchitailo
Biolase Inc., Irvine, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 October 2015; accepted 22 December 2015; published 25 December 2015
ABSTRACT
In this manuscript we discuss mass-varying neutrinos and propose their energy density to exceed that of baryonic and dark matter. We introduce cosmic Large Grains whose mass is about Planck mass, and their temperature is around 29 K. Large Grains are in fact Bose-Einstein condensates of proposed dineutrinos, and are responsible for the cosmic Far-Infrared Background (FIRB) radiation. The distribution of the energy density of all components of the World (protons, electrons, photons, neutrinos, and dark matter particles) is considered. We present an overview of the World- Universe Model (WUM) and pay particular attention to the self-consistent set of time-varying values of basic parameters of the World: the age and critical energy density; Newtonian parameter of gravitation and Hubble’s parameter; temperatures of the cosmic Microwave Background radiation and the peak of the cosmic FIRB radiation; Fermi coupling parameter and coupling parameters of the proposed Super-Weak and Extremely-Weak interactions. Additionally, WUM forecasts the masses of dark matter particles, axions, and neutrinos; proposes two fundamental parameters of the World: fine-structure constant α and the quantity Q which is the dimensionless value of the fifth coordinate, and three fundamental physical units: basic unit of momentum, energy density, and energy flux density. WUM suggests that all time-dependent parameters of the World are inter- connected and in fact dependent on Q. We recommend adding the quantity Q to the list of the CODATA-recommended values.
Keywords:
5D World-Universe Model, Medium of the World, Mass-Varying Neutrinos, Dineutrinos, Bose- Einstein Condensates, Far-Infrared Background Radiation, Time-Varying Parameters of the World

1. Introduction
We can’t solve problems by using the same kind of thinking we used when we created them.
―Albert Einstein
The role of the Intergalactic plasma consisting of protons, electrons, and photons as part of the Medium of the World is analyzed in [1] . The Multicomponent Dark Matter and its decisive role in the Medium and Macroobjects of the World are discussed in [2] .
Mass-varying neutrinos as part of the Medium of the World are analyzed in Section 2.1. The distribution of the energy density of all components of the World (protons, electrons, photons, neutrinos, and dark matter particles) is considered in Section 2.2. In Section 3 we propose a new physical model for the cosmic Far-Infrared Background (FIRB) radiation based on Bose-Einstein condensates of cosmic dineutrinos. In Section 4 we present an overview of World-Universe Model (WUM) and pay particular attention to time-varying values of the basic parameters of the World.
In 5D WUM [1] [2] we introduced
・ a basic unit of mass
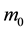 that equals to
that equals to
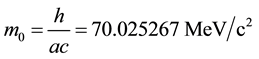 (1.1)
(1.1)
where h is Planck constant, c is the electrodynamic constant,
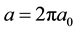 , and
, and
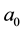 is the classical electron radius;
is the classical electron radius;
・ a dimensionless time-varying quantity Q which equals to the ratio of the size of the World R at cosmological time τ to the Worlds’ size a at the Beginning:
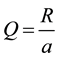 (1.2)
(1.2)
In WUM, neutrino masses are related to and proportional to
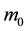 multiplied by fundamental parameter
multiplied by fundamental parameter
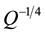 and different coefficients that will be discussed in Section 2.1.
and different coefficients that will be discussed in Section 2.1.
2. Components of the World
2.1. Mass-Varying Neutrinos
It is now established that there are three different types of neutrino: electronic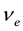 , muonic
, muonic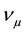 , and tauonic
, and tauonic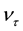 , and their antiparticles. B. Pontecorvo and Y. Smorodinsky discussed the possibility of energy density of neutrinos exceeding that of baryonic matter [3] . Neutrino oscillations imply that neutrinos have non-zero masses [4] [74] .
, and their antiparticles. B. Pontecorvo and Y. Smorodinsky discussed the possibility of energy density of neutrinos exceeding that of baryonic matter [3] . Neutrino oscillations imply that neutrinos have non-zero masses [4] [74] .
Let’s take neutrino masses
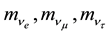 that are near
that are near
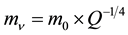 (2.1)
(2.1)
Their concentrations
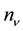 are then proportional to
are then proportional to
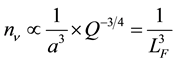 (2.2)
(2.2)
where
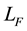 is the Fermi length parameter:
is the Fermi length parameter:




where


quently to


Experimental results obtained by M. Sanchez [5] show



and



where


Significantly more accurate result was obtained by P. Kaus, et al. [6] for the ratio of the mass splitting:

Let’s assume that muonic neutrino’s mass indeed equals to

From equation (2.8) it then follows that

Then the squared values of the muonic and tauonic neutrino masses fall into ranges (2.6) and (2.7):

Let’s assume that electronic neutrino mass equals to

The assumptions made in (2.9) and (2.12) are further supported by the excellent numerical agreement of calculated and measured value of fine-structure constant

The calculated neutrino masses are in a good agreement with masses found in [7] :

and with experimental values obtained in [8] [9] . The sum of the calculated neutrino masses

is also in a good agreement with the value of

Considering that all elementary particles, including neutrinos, are fully characterized by their four-momentum


we obtain the following neutrino energy densities


where





Let’s take the following value for Fermi momentum

where



neutrinos relative energy densities



where

It’s commonly accepted that concentrations of all types of neutrinos are equal. This assumption allows us to calculate the total neutrinos relative energy density in the Medium:

One of the principal ideas of WUM holds that energy densities of Medium particles are proportional to proton energy density in the World’s Medium [1] :

which depends on the fundamental parameter


which is remarkably close to its value calculated in (2.24).
2.2. Distribution of the World’s Energy Density
According to WUM energy density of all Macroobjects of the World







Our Model holds that the energy density of all types of Dark Matter Particles (DMP) is proportional to the proton energy density


In all, there are 5 different types of DMP: Neutralinos, WIMPs, DIRACs, ELOPs, and Sterile Neutrinos with the anticipating masses of 1.3 TeV, 9.6 GeV, 70 MeV, 340 keV, and 3.7 keV [2] . Then the total energy density of DM


which is close to the DM energy density measured in literature [12] :
An alternative interesting approach to Dark Matter is given by extended theories of gravity, as it has been shown by Prof. Christian Corda in [36] .
The total baryonic energy density


The sum of electron and Microwave Background Radiation (MBR) energy densities


We took additional energy density

so that the energy density of the World


We will connect the chosen value of

From (2.33) we can calculate the value of

which is in excellent agreement with the commonly adopted value of 137.035999074 (44) and proves our assumptions about electronic neutrino mass (2.12), neutrinos energy density of the Medium (2.26), and additional energy density (2.32) that is discussed in Section 3.
It follows that there is a direct correlation between constants



from α.
To summarize:
・ The World’s energy density is proportional to the Fundamental parameter
・ The particles relative energy densities are proportional to Fundamental constant
・ The total neutrinos energy density is almost 10 times greater than baryonic energy density, and about 3 times greater than Dark Matter energy density.
3. Cosmic Far-Infrared Background
The cosmic Far-Infrared Background (FIRB), which was announced in January 1998, is part of the Cosmic Infrared Background (CIB), with wavelengths near 100 microns that is the peak power wavelength of the black body radiation at temperature 29 K. In this Section we introduce Bose-Einstein Condensate (BEC) drops of dineutrinos whose mass is about Planck mass, and their temperature is around 29 K. These drops are responsible for the FIRB.
3.1. Observations
Infrared Astronomical Satellite (IRAS) mission was the first all-sky survey which used far-infrared wavelengths in 1983. Using IRAS, scientists were able to determine the luminosity of the galactic objects discovered. Over 250,000 infrared sources were observed during the 10 month mission.
The FIRB radiation was observed for different galaxies in [13] - [32] . M. G. Hauser, et al. revealed bright emission from interplanetary dust at 100 microns [13] . F. J. Low, et al. pointed out that the 100 micrometer cirrus may represent cold material in the outer solar system or a new component of the interstellar medium [14] .
B. Wang in 1991 found that the integrated FIRB from galaxies peaks at around 100 - 130 microns, with total radiation density from 0.5% to 6% of the cosmic MBR [15] . E. L. Wright in 1999 recomputed of FIRB and found its total intensity to be about 3.4% of the MBR intensity [16] .
In 1999, G. Lagache, et al. described the cosmic FIRB and announced that for the first time the far-IR emission of dust associated with the Warm Ionized Medium (WIM) is evidenced. The best representation of the WIM dust spectrum is obtained for a temperature of 29.1 K [21] . D. P. Finkbeiner, et al. have detected substantial flux in the 100 micron channel in excess of expected zodiacal and Galactic emission. They concluded that there is currently no satisfactory explanation for the 100 micron excess [22] .
M. J. Devlin, et al. have this to say about a population of luminous, high-redshift, dusty starburst galaxies: In the redshift range 1 ≤ z ≤ 4, these massive submillimetre galaxies go through a phase characterized by optically obscured star formation at rates several hundred times that in the local Universe. Half of the starlight from this highly energetic process is absorbed and thermally reradiated by clouds of dust at temperatures near 30 K with spectral energy distributions peaking at 100 μm [29] .
3.2. Model
According to [33] - [35] , the size of large cosmic grains



and their mass



The density of grains


According to WUM, Planck mass


Note that the value of



A grain of mass



where


The received energy will increase the grain’s temperature

where


and

With Nikola Tesla’s principle at heart―There is no energy in matter other than that received from the environment―we apply the World equation [2] to a grain:

where


We then calculate the grain’s stationary temperature


This result is in an excellent agreement with experimentally measured value of 29 K [21] - [32] .
Cosmic FIRB radiation is not a black body radiation. Otherwise, its energy density



The total flux of the FIRB radiation is the sum of the contributions of all individual grains.
WUM calculates the value of the MBR temperature


Comparing Equations (3.11) and (3.13), we can find the relation between the grains’ temperature and the temperature of the MBR:

where electron relative energy density



3.3. Planck Mass
The developed FIRB model introduces Large Grains whose mass is about Planck mass

where n is an integer,


Taking into account the analogy between electromagnetic and gravitoelectromagnetic fields, we can rewrite the same equation for masses of a gravitoelectromagnetic field:

where


Two particles or microobjects will not exert gravity on one another when both of their masses are smaller than the Planck mass. Planck mass can then be viewed as the mass of the smallest macroobject capable of generating the gravitoelectromagnetic field.
3.4. Mass-Varying Quants: Axions and Dineutrinos
According to WUM, all “elementary” particles of the World are fermions and they possess masses. Bosons such as photons, X-rays, and gamma rays are composite particles and consist of an even numbers of fermions. An axion is a boson possessing the lowest rest mass


which is decreasing in time:



which is about 10 orders of magnitude larger than the axion mass and is decreasing in time:
According to WUM, the total neutrinos energy density in the World is almost 10 times greater than baryonic energy density, and about 3 times greater than Dark Matter energy density (Section 2.2). At high neutrinos concentration, we can expect “neutrino pairs”

3.5. Bose-Einstein Condensate
New cosmological models employing the Bose-Einstein Condensates (BEC) have been actively discussed in literature in recent years [49] - [63] . The transition to BEC occurs below a critical temperature

where



According to our Model, we can take the value of the critical temperature




Taking into account equations (3.11), (3.21) and (3.23), we can calculate the value of

and the value of the mass


The calculated values of the mass and concentration of dineutrinos satisfy the conditions for their Bose-Eins- tein condensation. Consequently, BEC drops whose masses are about Planck mass can be created. The stability of such drops is provided by the detailed equilibrium between the energy absorption from the Medium of the World (provided by dineutrinos as a result of their Bose-Einstein condensation) and re-emission of this energy in FIRB at the stationary temperature

The FIRB energy density


which is


The ratio between FIRB and MBR corresponds to the value of 3.4% calculated by E. L. Wright [16] .
3.6. Star Creation
In our opinion, the BEC drops with mass around



Formation of a new star starts with a gravitational instability of the cloud of BEC drops and subsequent gravitational collapse of them, with the resulting macroobject (Core) possessing mass about

A density of Core can be up to the nuclear density


Then according to equation (3.18), all particles heavier than m0 (neutralinos, WIMPs, protons) will be attracted to this Core, increasing its mass and attracting lighter particles (DIRACs, ELOPs, sterile neutrinos) which form Shells around the Core [2] .
3.7. Conclusion
In this Section we proposed the existence of BEC drops of dineutrinos whose mass is about Planck mass, and temperature of around 29 K. BEC drops are responsible for the FIRB and explain the substantial 100 micron flux in excess of expected zodiacal and Galactic emission.
In our opinion, BEC drops are the smallest building blocks of all macroobjects. Since the drops possess Planck mass, they can be reasoned about from the standpoint of classical physics, validating our calculations of the drops’ masses and temperature.
BEC drops do not absorb and re-emit starlight. Instead, they absorb energy directly from the Medium of the World (provided by dineutrinos). We can thus explain the existence of ultra-luminous infrared galaxies in a very active star formation period, which are extremely bright in the infrared spectrum and at the same time faint (often almost invisible) in the optical spectrum (see review papers [64] [65] and references therein).
4. The World
5D World-Universe Model is based on the following primary assumptions:
・ The universality of physical laws;
・ The cosmological principle which states that on a large scale the World is homogeneous and isotropic;
・ The World is finite and is expanding inside the 4-dimensional Universe with speed equal to the gravitoelectrodynamic constant c;
・ The Medium of the World, consisting of protons, electrons, photons, neutrinos, and dark matter particles (DMP) is an active agent in all physical phenomena in the World.
The Model is based on Maxwell’s equations for electromagnetism and gravitoelectromagnetism which have two measurable characteristics: energy density ρ and energy flux density I. All other notions are used for calculations of these two measurable characteristics.
In our discussion we have utilized the particles’ four-momentum; however, the final result of the statistical analysis is energy density.
Two Fundamental Parameters in various rational exponents define all macro and micro features of the World: fine-structure constant α and dimensionless quantity Q. While α is constant, Q increases with time, and is in fact the dimensionless fifth coordinate in our Model.
Three Fundamental Units define all physical dimensional parameters of the World: basic unit of momentum


4.1. WUM Overview
The World was started by a fluctuation in the 4-dimensional Universe, and the Nucleus of the World, which is a 4-ball, was born. The Nucleus antipode length (the furthest distance between any two points of the Nucleus 3-sphere) at the Beginning was equal to a. The Nucleus has since been expanding through the Universe so that the antipode length R is increasing with speed c for cosmological time


The World consists of the Medium (protons, electrons, photons, neutrinos, and dark matter particles) and Macroobjects (Galaxy clusters, Galaxies, Star clusters, Extrasolar systems, planets, etc. down to BEC drops) made of these particles. DMP include three Majorana fermions (Neutralinos, WIMPs, and Sterile neutrinos) with spin of 1/2 and two spin-0 bosons (named DIRACs and ELOPs in the WUM) [2] . According to WUM, all stable particles are created in the 3-sphere World due to the surface energy of the 4-ball Nucleus of the World provided by the 4-dimensional Universe [1] .
The Medium of the World composed of massive particles is the manifestation of the metric depending on

The principal idea of WUM is that the energy density of the World


The black body spectrum of the cosmic Microwave Background Radiation (MBR) is due to thermodynamic equilibrium of photons with low density intergalactic plasma. The calculated by the equation (3.13) value of MBR temperature


Nucleosynthesis of all elements (including light elements) occurs inside stars during their evolution (Stellar nucleosynthesis). The theory of this process is well developed, starting with the publication of a celebrated B2FH review paper in 1957 [69] . With respect to WUM, stellar nucleosynthesis theory should be enhanced to account for annihilation of heavy DMP (WIMPs and Neutralinos) [2] . The amount of energy produced due to this process is sufficiently high to produce all elements inside stellar cores.
All Macroobjects (MO) of the World (galaxy clusters, galaxies, star clusters, extrasolar systems, and planets) have cores made up of different DMP surrounded by different shells [2] . We have developed the model of the World that describes MO possessing energies proportional to the total World’s macroobjects energy

・ World: 1
・ Galaxy clusters:
・ Galaxies:
・ Globular clusters:
・ Extrasolar systems:
The energy consumption rates are greater for galaxies relative to extrasolar systems, and for the World relative to galaxies. It follows that new stars and star clusters can be created inside of a galaxy, and new galaxies and galaxy clusters can arise in the World. Structures form from top (the World) down to extrasolar systems in parallel around different cores made of different DMP. Formation of galaxies and stars is not a process that concluded ages ago; instead, it is ongoing.
The World is continuously receiving energy from the Universe that envelopes it. Assuming an unlimited Universe, the numbers of cosmological structures on all levels will increase: new galaxy clusters will form; existing clusters will obtain new galaxies; new stars will be born inside existing galaxies; sizes of individual stars will increase, etc. The temperature of the Medium of the World will asymptotically approach absolute zero (see equation (3.13)).
4.2. Time-Varying Parameters of the World
In accordance with WUM, the dimensionless quantity Q in various rational exponents defines all time-varying parameters of the World as follows [1] :
・ Total energy of the World


・ Newtonian parameter of gravitation G

・ Hubble’s parameter H

・ Age of the World

・ Size of the World R

・ Critical energy density

・ Planck mass

・ Temperature of the microwave background radiation

・ Temperature of the far-infrared background radiation peak

・ Fermi coupling parameter

where the basic unit of energy


All parameters of the World depending on Q are a manifestation of the fifth dimension of the World [1] . Their calculated values are in good agreement with the experimentally measured values.
The calculated values of the parameter






The value of


To summarize: parameters









4.3. Grand Unified Theory
The Grand Unified Theory is a model in particle physics in which at high energy, the three interactions―Weak, Electromagnetic, and Strong, are merged into one single interaction characterized by one Unified Coupling constant. By definition: Coupling constant is a number that determines the strength of an interaction. For example, the gravitational coupling constant


where




At an atomic scale, the strong interaction is about 100 times stronger than electromagnetic interaction, which in turn is about 1010 times stronger than the weak force, and about 1040 times stronger than the gravitational force, when forces are compared between particles interacting in more than one way.
All these definitions are based on strength of the force between a particular pair of particles, and depend on the choice of such particles. Clearly, the gravity between a pair of electrons will differ from that of a pair of protons. In our opinion, there is no gravitational interaction between elementary particles (see Section 3.3).
In this Section we propose a different way of comparing interactions based on Fundamental parameter Q in various rational exponents. Let’s start with the gravitational interaction which is expressed by gravitational parameter G:

Let’s take a dimension-transposing parameter



and divide the interaction parameter


where parameter


By dividing the left side of (4.18) by



Using the same approach for electromagnetic interaction, we divide the charge e by the magnetic dipole of dark matter particle DIRAC

and multiply the interaction parameter


The dimensionless electromagnetic coupling parameter


The ratio of the coupling parameters is

The coupling parameter



The difference between the strong and the electromagnetic interactions lies not in their coupling parameters but in the strength of these interactions depending on the particles involved: electrons with charge e and monopoles with charge

in electromagnetic and strong interactions respectively.
The weak interaction is about 1010 times weaker than electromagnetic. We can therefore assume that its coupling parameter





Substituting the value of



that is in excellent agreement with the commonly adopted value of
At the very Beginning (


At that time, the extrapolated energy density of the World


Note that the energy density at the Beginning is much smaller than the nuclear density

The gravitational coupling parameter


The weak coupling parameter is decreasing as follows:

The strong and electromagnetic parameters remain constant in time:

Our Model foresees two more types of interactions:
・ Super-Weak, coupling parameter

・ Extremely-Weak, coupling parameter

According to WUM, the super-weak interaction is

Acknowledgements
I am very grateful to Felix Lev and my son Ilya Netchitailo for valuable stimulating discussions of the Model.
Cite this paper
Vladimir S.Netchitailo, (2016) 5D World-Universe Model. Neutrinos. The World. Journal of High Energy Physics, Gravitation and Cosmology,02,1-18. doi: 10.4236/jhepgc.2016.21001
References
- 1. Li, M.-H. and Li, Z.-B. (2014) Constraints on Bose-Einstein-Condensed Axion Dark Matter from the HI nearby Galaxy Survey Data. Physical Review D, 89, Article ID: 103512. http://dx.doi.org/10.1103/physrevd.89.103512
- 2. Morikawa, M. (2004) Structure Formation through Cosmic Bose Einstein Condensation-Unified View of Dark Matter and Energy. 22nd Texas Symposium on Relativistic Astrophysics, Stanford, 13-17 December 2004, 1122.
- 3. Garay, L.J., Anglin, J.R., Cirac, J.I. and Zoller, P. (2000) Sonic Analog of Gravitational Black Holes in Bose-Einstein Condensates. Physical Review Letters, 85, 4643-4647. http://dx.doi.org/10.1103/physrevlett.85.4643
- 4. Ueda, M. and Huang, K. (1998) Fate of a Bose-Einstein Condensate with Attractive Interaction. arXiv: 9807359.
- 5. Hujeirat, A.A. (2011) On the Viability of Gravitational Bose-Einstein Condensates as Alternatives to Supermassive Black Holes. Monthly Notices of the Royal Astronomical Society, 423, 2893-2900.
- 6. Kuhnel, F. and Sundborg, B. (2014) Decay of Graviton Condensates and their Generalizations in Arbitrary Dimensions. Physical Review D, 90, Article ID: 064025. http://dx.doi.org/10.1103/physrevd.90.064025
- 7. Hauser, M.G. and Dwek, E. (2001) The Cosmic Infrared Background: Measurements and Implications. Annual Review of Astronomy & Astrophysics, 39, 249-307.
- 8. Kashlinsky, A. (2005) Cosmic Infrared Background and Early Galaxy Evolution. Physics Reports, 409, 361-438. http://dx.doi.org/10.1016/j.physrep.2004.12.005
- 9. Wesson, P.S. (1983) A New Approach to Scale-Invariant Gravity. Astronomy & Astrophysics, 119, 145-152.
- 10. Overduin, J.M. and Wesson, P.S. (1998) Kaluza-Klein Gravity. Physics Reports, 283, 303-380.
- 11. Fixsen, D.J. (2009) The Temperature of the Cosmic Microwave Background. The Astrophysical Journal, 707, 916-920. http://dx.doi.org/10.1088/0004-637x/707/2/916
- 12. Burbidge, E.M., Burbidge, G.R., Fowler, W.A. and Hoyle, F. (1957) Synthesis of the Elements in Stars. Reviews of Modern Physics, 29, 547-650. http://dx.doi.org/10.1103/RevModPhys.29.547
- 13. Wolfenstein, L. (1994) Superweak Interactions. Comments on Nuclear and Particle Physics, 21, 275.
- 14. Yamaguchi, Y. (1959) Possibility of Super-Weak Interactions and the Stability of Matter. Progress of Theoretical Physics, 22, 373-380. http://dx.doi.org/10.1143/PTP.22.373
- 15. Kelley, K.F. (1999) Measurement of the CP Violation Parameter . PhD Thesis, MIT, Cambridge, MA.
- 16. Bian, B.A., Feng, Z.Q., Li, W.F., Ming, Z.Y., Chen, L.W., Jin, G.M., et al. (2006) Determination of the NN Cross Section, Symmetry Energy, and Studying of Weak Interaction in CSR. http://ribll.impcas.ac.cn/conf/ccast05/doc/RIB05-zhangfengshou.pdf
- 17. McDonald, A.B. (2003) Neutrino Properties from Measurements using Astrophysical and Terrestrial Sources. arXiv: 0310775.
- 18. Davidson, S. and Elmer, M. (2013) Bose Einstein Condensation of the Classical Axion Field in Cosmology? Journal of Cosmology and Astroparticle Physics, 2013, Article No.: 034.
- 19. Banik, N. and Sikivie, P. (2013) Axions and the Galactic Angular Momentum Distribution. Physical Review D, 88, Article ID: 123517. http://dx.doi.org/10.1103/physrevd.88.123517
- 20. Erken, O., Sikivie, P., Tam, H. and Yang, Q. (2011) Axion BEC Dark Matter. arXiv: 1111.3976.
- 21. Sikivie, P. and Yang, Q. (2009) Bose-Einstein Condensation of Dark Matter Axions. Physical Review Letters, 103, Article ID: 111301. http://dx.doi.org/10.1103/physrevlett.103.111301
- 22. Diez-Tejedor, A., Gonzalez-Morales, A.X. and Profumo, S. (2014) Dwarf Spheroidal Galaxies and Bose-Einstein Condensate Dark Matter. Physical Review D, 90, Article ID: 043517. http://dx.doi.org/10.1103/physrevd.90.043517
- 23. Suarez, A., Robles, V.H. and Matos, T. (2013) A Review on the Scalar Field/Bose-Einstein Condensate Dark Matter Model. In: González, C.M., Aguilar, J.E.M. and Barrera, L.M.R., Eds., Accelerated Cosmic Expansion, Springer, Berlin, 107-142.
- 24. Magana, J., and Matos, T. (2012) A Brief Review of the Scalar Field Dark Matter Model. Journal of Physics: Conference Series, 378, Article ID: 012012. http://dx.doi.org/10.1088/1742-6596/378/1/012012
- 25. Robles, V.H. and Matos, M. (2012) Flat Central Density Profile and Constant DM Surface Density in Galaxies from Scalar Field Dark Matter. Monthly Notices of the Royal Astronomical Society, 422, 282-289.
- 26. Sin, S.-J. (1992) Late Time Cosmological Phase Transition and Galactic Halo as Bose-Liquid. arXiv: 9205208.
- 27. Oussoren, K. (2015) Angular Analysis in HWW. ATLAS Outing 2015. https://indico.nikhef.nl/getFile.py/access?contribId=6&sessionId=0&resId=0&materialId=slides&confId=145
- 28. Hall, D.C. (2014) Discovery and Measurement of the Higgs Boson in the WW Decay Channel. PhD Thesis, University of Oxford, Oxford. http://inspirehep.net/record/1339842/files/CERN-THESIS-2014-130.pdf
- 29. Hoonhout, B. (2014) Higgs Spin Analysis in Collins-Soper Frame Using Opening Angles of Different-Flavour Final State. PhD Thesis, Amsterdam University, Amsterdam. https://esc.fnwi.uva.nl/thesis/centraal/files/f40866552.pdf
- 30. Li, X.-Q., Yang, Y.-D. and Yuan, X.-B. (2012) Anomalous tqZ Coupling Effects in Rare B- and K-Meson Decays. Journal of High Energy Physics, 2012, Article No.: 18.
- 31. Würthwein, F. (2011) Search for Higgs in the Dilepton Dineutrino Final State with CMS. UCSD, San Diego. http://uaf-2.t2.ucsd.edu/~fkw/ggi-2011.pdf
- 32. Sharafiddinov, R.S. (2011) An Axial Vector Nature of a Neutrino with an Electroweak Mass. Acta Radiologica, 42, 291-293.
- 33. del Amo Sanchez, P., et al. (2011) Search for the Rare Decay B->K nu nubar. Physical Review D, 82, Article ID: 112002.
- 34. Straub, D.M. (2010) Supersymmetry, the Flavour Puzzle and Rare B Decays. PhD Thesis, Munich Technical University, Munich. https://mediatum.ub.tum.de/doc/981472/981472.pdf
- 35. Altmannshofer, W., Buras, A.J., Straub, D.M. and Wick, M. (2009) New Strategies for New Physics Search in B -> K* nu anti-nu, B -> K nu anti-nu and B -> X(s) nu anti-nu Decays. Journal of High Energy Physics, 2009, Article No.: 022.
- 36. Samsonenko, N.V. (2007) Fundamental Interactions and Their Relative Contribution to the Nuclear Reactions at Low Energies. International Conference on Condensed Matter Nuclear Science, 125. http://newenergytimes.com/v2/conferences/2007/ICCF13/ICCF13-Abstracts.pdf
- 37. Cortina, G.E., et al. (1996) Study of Rare B Decays with the DELPHI Detector at LEP. http://hdl.handle.net/2078.1/123879
- 38. Finkbeiner, D.P., Davis, M. and Schlegel, D.J. (1999) Extrapolation of Galactic Dust Emission at 100 Microns to CMBR Frequencies Using FIRAS. The Astrophysical Journal, 524, 867-886.
- 39. Fixsen, D.J., Cheng, E.S., Gales, J.M., Mather, J.C., ShaFer, R.A. and Wright, E.L. (1996) The Cosmic Microwave Background Spectrum from the Full COBE* FIRAS Data Set. The Astrophysical Journal, 473, 576-587. http://dx.doi.org/10.1086/178173
- 40. Wright, E.L. (2001) Cosmic InfraRed Background Radiation. http://www.astro.ucla.edu/~wright/CIBR/
- 41. Wang, B. (1991) Integrated Far-Infrared Background from Galaxies. The Astrophysical Journal, 374, 465-474. http://dx.doi.org/10.1086/170136
- 42. Low, F.J., Young, E., Beintema, D.A., Gautier, T.N., Beichman, C.A., Aumann, H.H., Gillett, F.C., Neugebauer, G., Boggess, N. and Emerson, J.P. (1984) Infrared Cirrus-New Components of the Extended Infrared Emission. The Astrophysical Journal, 278, L19-L22. http://dx.doi.org/10.1086/184213
- 43. Hauser, M.G., Gillett, F.C., Low, F.J., Gautier, T.N., Beichman, C.A., Aumann, H.H., Neugebauer, G., Baud, B., Boggess, N. and Emerson, J.P. (1984) IRAS Observations of the Diffuse Infrared Background. The Astrophysical Journal, 278, L15-L18. http://dx.doi.org/10.1086/184212
- 44. NASA’s Planck Project Office (2013) Planck Mission Brings Universe into Sharp Focus. https://www.nasa.gov/mission_pages/planck/news/planck20130321.html#.VZ4k5_lViko
- 45. Landau, L.D. and Lifshitz, E.M. (1980) Statistical Physics. Third Edition, Part 1: Volume 5. Butterworth-Heinemann, Oxford.
- 46. Battye, R.A. and Moss, A. (2014) Evidence for Massive Neutrinos from CMB and Lensing Observations. arXiv: 1308.5870.
- 47. Maltoni, M., Schwetz, T., Tortola, M.A. and Valle, J.W.F. (2003) Status of Three-Neutrino Oscillations after the SNO- Salt Data. Physical Review D, 68, Article ID: 113010. http://dx.doi.org/10.1103/PhysRevD.68.113010
- 48. Gonzalez-Garcia, M.C. and Pena-Garay, C. (2003) Three-Neutrino Mixing after the First Results from K2K and KamLAND. Physical Review D, 68, Article ID: 093003. http://dx.doi.org/10.1103/PhysRevD.68.093003
- 49. Dermisek, R. (2004) Neutrino Masses and Mixing, Quark-Lepton Symmetry and Strong Right-Handed Neutrino Hierarchy. Physical Review D, 70, Article ID: 073016.
- 50. Kaus, P. and Meshkov, S. (2003) Neutrino Mass Matrix and Hierarchy. AIP Conference Proceedings, 672, 117. http://dx.doi.org/10.1063/1.1594399
- 51. Sanchez, M. (2003) Oscillation Analysis of Atmospheric Neutrinos in Soudan 2. PhD Thesis, Tufts University, Medford/Somerville. http://nu.physics.iastate.edu/Site/Bio_files/thesis.pdf
- 52. Kajita, T. (1998) Atmospheric neutrino results from Super-Kamiokande and Kamiokande—Evidence for νμ oscillations. arXiv: 9810001.
- 53. Pontecorvo B. and Smorodinsky, Y. (1962) The Neutrino and the Density of Matter in the Universe. Soviet Physics— JETP, 14, 173.
- 54. Netchitailo, V.S. (2015) 5D World-Universe Model. Multicomponent Dark Matter. Journal of High Energy Physics, Gravitation and Cosmology, 1, 55-71. http://dx.doi.org/10.4236/jhepgc.2015.12006
- 55. Netchitailo, V.S. (2015) 5D World-Universe Model. Space-Time-Energy. Journal of High Energy Physics, Gravitation and Cosmology, 1, 25-34. http://dx.doi.org/10.4236/jhepgc.2015.11003
- 56. Mannheim, P.D. (1978) Parity Violation and the Masslessness of the Neutrino. http://www.osti.gov/scitech/servlets/purl/6506305/
- 57. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282. http://dx.doi.org/10.1142/s0218271809015904
- 58. Jackson, A.A. and Zook, H.A. (1991) Dust Particles from Comets and Asteroids: Parent-Daughter Relationships. Abstracts of the Lunar and Planetary Science Conference, 22, 629-630.
- 59. Saxton, J.M., Knotts, S.F., Turner, G. and Maurette, M. (1992) 40Ar/39Ar Studies of Antarctic Micrometeorites. Meteoritics, 27, 285.
- 60. Maurette, M., Cragin, J. and Taylor, S. (1992) Cosmic Dust in 50 KG Blocks of Blue Ice from Cap-Prudhomme and Queen Alexandra Range, Antarctica. Meteoritics, 27, 257.
- 61. Serra, P., Lagache, G., Doré, O., Pullen, A. and White, M. (2014) Cross-Correlation of Cosmic Infrared Background Anisotropies with Large Scale Structures. Astronomy & Astrophysics, 570, A98. http://dx.doi.org/10.1051/0004-6361/201423958
- 62. Mackenzie, T., Braglia, F.G., Gibb, A.G., Scott, D., Jenness, T., Serjeant, S., et al. (2011) A Pilot Study for the SCUBA-2 “All-Sky” Survey. Monthly Notices of the Royal Astronomical Society, 415, 1950-1960.
- 63. Chapin, E.L., Chapman, S.C., Coppin, K.E., Devlin, M.J., Dunlop, J.S., Greve, T.R., et al. (2011) A Joint Analysis of BLAST 250-500 um and LABOCA 870 um Observations in the Extended Chandra Deep Field-South. Monthly Notices of the Royal Astronomical Society, 411, 505-549.
- 64. Devlin, M.J., Ade, P.A.R., Aretxaga, I., Bock, J.J., Chapin, E.L., Griffin, M., et al. (2009) Over Half of the Far-Infrared Background Light Comes from Galaxies at z ≥ 1.2. Nature, 458, 737-739. http://dx.doi.org/10.1038/nature07918
- 65. Marshall, J.A., Herter, T.L., Armus, L., Charmandaris, V., Spoon, H.W.W., Bernard-Salas, J. and Houck, J.R. (2007) Decomposing Dusty Galaxies. I. Multi-Component Spectral Energy Distribution Fitting. The Astrophysical Journal, 670, 129-155.
- 66. Pope, A., Scott, D., Dickinson, M., Chary, R.-R., Morrison, G., Borys, C. and Sajina, A. (2006) Using Spitzer to Probe the Nature of Submillimetre Galaxies in GOODS-N. arXiv: 0603409.
- 67. Aguirre, J.E., Bezaire, J.J., Cheng, E.S., Cottingham, D.A., Cordone, S.S., Crawford, T.M., et al. (2003) The Spectrum of Integrated Millimeter Flux of the Magellanic Clouds and 30-Doradus from TopHat and DIRBE Data. The Astrophysical Journal, 596, 273-286. http://dx.doi.org/10.1086/377601
- 68. Dupac, X., et al. (2003) The Complete Submillimeter Spectrum of NGC 891. arXiv: 0305230.
- 69. Phillips, T.G. and Keene, J. (1992) Submillimeter Astronomy [Heterodyne Spectroscopy]. Proceedings of the IEEE, 80, 1662-1678. http://dx.doi.org/10.1109/5.175248
- 70. Siegel, P.H. (2002) Terahertz Technology. IEEE Transactions on Microwave Theory and Techniques, 50, 910-928. http://dx.doi.org/10.1109/22.989974
- 71. Finkbeiner, D.P., Davis, M. and Schlegel, D.J. (2000) Detection of a Far IR Excess with DIRBE at 60 and 100 Microns. The Astrophysical Journal, 544, 81-97.
- 72. Lagache, G., Abergel, A., Boulanger, F., Désert, F.X. and Puget, J.-L. (1999) First Detection of the Warm Ionized Medium Dust Emission. Implication for the Cosmic Far-Infrared Background. Astronomy and Astrophysics, 344, 322-332.
- 73. Finkbeiner, D.P. and Schlegel, D.J. (1999) Interstellar Dust Emission as a CMBR Foreground. The Astrophysical Journal, 524, 867-886.
- 74. Draine, B.T. and Lazarian, A. (1998) Electric Dipole Radiation from Spinning Dust Grains. The Astrophysical Journal, 508, 157-179. http://dx.doi.org/10.1086/306387
















