Department of Physics, University of Houston Clear Lake, Houston, USA
Email: masood@uhcl.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 March 2015; accepted 9 May 2015; published 13 May 2015
ABSTRACT
We recalculate the magnetic moment of neutrinos in a hot and dense medium. The magnetic dipole moment of neutrinos is modified at high temperature and chemical potential. We show that the magnetic dipole moment of electron neutrino does not get a significant contribution from thermal background to meet the cosmological bound. However, chemical potential contribution to the magnetic moment is non-ignorable even when chemical potential is an order of magnitude greater than the electron mass. It is demonstrated that this effect is more significant in the models with an extended Higgs sector through neutrino mixing.
Keywords:
Neutrino, Magnetic Moment, Hot and Dense Medium

1. Introduction
Neutrinos were originally discovered as massless neutral fermions. These fermions can only interact weakly and conserve individual lepton number in the standard electroweak model (SEWM). Neutrinos are massless left- handed fermions in SEWM and are called Weyl neutrinos. These left-handed neutrinos can interact weakly with leptons (of the same flavor) and quarks. On the other hand, the neutrino oscillation (flavor or spin) is only allowed with nonzero mass of neutrino, though this mass can be small enough to give ignorable contributions to beta decay. However, neutrinos can oscillate among different flavors if they have nonzero mass and a right- handed partner. A very tiny nonzero mass of neutrino leads to the numerous extensions of the standard model and opens up new venues of research in high energy physics with its tremendous applications to astroparticle physics and cosmology. Minimally extended standard model (MESM) still obeys the law of conservation of individual lepton number. In this paper, we look at the MESM with nonzero tiny Dirac mass which does not change the SEWM, other than adding an inert right-handed neutrino as a singlet in each generation.
Massless neutrinos are represented by Weyl spinners with one degree of freedom. These Weyl neutrinos have to strictly obey the conservation of individual lepton number. However, nonzero mass [1] of neutrino was originally suggested to resolve Solar Neutrino Problem (SNP). Neutrino mixing or neutrino oscillation is a natural consequence of massive neutrino, though extremely small. SEWM allows two types of massive neutrinos: Dirac neutrinos bring in a right-handed neutrino as an anti-particle with equal and opposite mass, whereas Majorana mass adds a heavy right-handed neutrino for seesaw mechanism. Massive neutrino with a Dirac mass can establish a higher order coupling with the magnetic field through radiative corrections and has nonzero magnetic moment which is induced by the corresponding charged lepton. The Majorana neutrino can have the transition magnetic moment that is also associated with the coupling of neutrino with charged leptons and is called transition magnetic moment. However, the transition magnetic moment can be expressed in terms of the magnetic dipole moment of Dirac neutrino [2] -[6] .
Superkamiokande claimed the experimental evidence of neutrino oscillations [7] -[9] , indicating nonzero mass of neutrino as a possible solution of SNP. This nonzero mass of neutrino encouraged phenomenologists to study the properties of massive neutrinos in detail and look for other applications of nonzero mass of neutrino. If the neutrino mass is not exactly equal to zero, then we can think about the existence of right-handed neutrino as well. Now, to accommodate this right handed neutrino in the SM, we have to look for different extensions of the SM. These tiny masses of neutrinos, though they are not expected to be high enough to change the physical results significantly, provide enough motivations to look at the extensions of the standard electroweak model, even more seriously. In this paper, we will work on MESM, mainly. All the Feynman diagrams and the corresponding rules of the SM remain unchanged in this model.
MESM can further be extended with increased particle sectors associated with the modified conservation rules. In one of the simplest model, we have to extend the Higgs sector to accommodate the neutrino doublet in the theory at the expense of the individual lepton number. Total lepton number is always conserved. This new charged Higgs can be added as a singlet [10] or as a doublet [11] . We would refer to the last one as the Higgs doublet model (HDM) throughout this paper and look at it as an example of possible extension of SEWM, with embedded neutrino mixing. There are several other extensions of the standard model which we do not include in our discussions, because we mainly want to calculate the quantum statistical background effects on the properties of massive neutrinos. Although the neutrino masses are small enough to be ignored in most cases, we still have to investigate the behavior of massive neutrinos in astrophysical and cosmological environments where they behave differently with this tiny mass. Astronomical environments can be extremely hot and dense with strong magnetic field. We study the behavior of Weyl neutrino in the constant magnetic field. Our basic scheme of work is real-time formalism [12] - [18] where we deal with the real particles processes in the heat bath of real particles at moderate energies.
This paper has been organized in a way that the next section is devoted to the study of the properties of massless neutrino in a strong magnetic field in extremely dense systems. Properties of Dirac neutrinos at finite temperature and density are calculated in Section 3 for different ranges of temperature and chemical potential. Majorana neutrinos are not discussed in detail because the transition magnetic moment of Majorana neutrinos [2] can be expressed in terms of the magnetic moment of Dirac neutrino. In the last section, we discuss all of the calculated results and their implications.
2. Weyl Neutrino
Weyl Neutrinos are massless neutrinos and conserve the individual lepton number. It does not interact with the medium directly. Weyl neutrinos, being massless neutral particles, do not couple with the magnetic field, even at extremely high temperatures. However, they can acquire a dynamically generated shielding mass like other neutral particles [15] -[18] due to its interaction with electrons in an extremely dense rotating system with a high concentration of charged particles such as electrons. With this effective mass, a neutrino will behave as a Dirac particle with the effective mass [19]
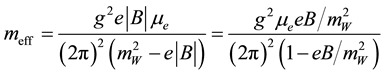 (1)
(1)
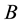 is the constant magnetic field and
is the constant magnetic field and 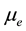 gives the chemical potential of electrons in the background. Equation (1) can later be inserted in the magnetic moment expression to get the magnetic moment of neutrino, corresponding to the dynamically generated mass and is treated as Dirac mass. This effective mass of neutrino increases with increasing magnetic field, whereas W boson mass sets an upper limit on the magnetic field, that is;
gives the chemical potential of electrons in the background. Equation (1) can later be inserted in the magnetic moment expression to get the magnetic moment of neutrino, corresponding to the dynamically generated mass and is treated as Dirac mass. This effective mass of neutrino increases with increasing magnetic field, whereas W boson mass sets an upper limit on the magnetic field, that is; 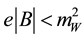 to get the physically acceptable effective mass. In this equation, Equation (1) is used to calculate the rate of change of this mass with the constant magnetic field comes out to be [19]
to get the physically acceptable effective mass. In this equation, Equation (1) is used to calculate the rate of change of this mass with the constant magnetic field comes out to be [19]
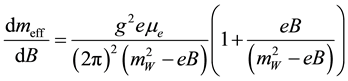 , (2)
, (2)
Equation (2) gives the coupling of neutrino through its dynamically generated mass 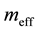 and
and 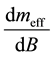 which
which
is proportional to the magnetic moment of neutrino and is proportional to the chemical potential of the corresponding charged lepton of the same generation. Rate of change of the effective mass with respect to the constant magnetic field of the medium is independent of temperature. Weyl neutrino cannot interact with thermal medium. For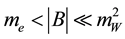 , we can write it as
, we can write it as
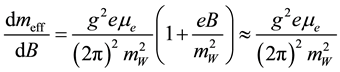 , (3)
, (3)
and, for very large magnetic field
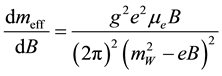 , (4)
, (4)
which is simply ignorable until the chemical potential 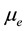 is very large. Equation (2) can also be rewritten as
is very large. Equation (2) can also be rewritten as
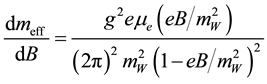 . (5)
. (5)
The above equation indicates that the coupling with the weak magnetic field depends on the magnetic field itself. However, for strong field, the effective magnetic moment is constant and will be significant only if the chemical potential is large enough.
Just to understand the functional behavior of the effective mass, we plot the effective mass (Figure 1) and the rate of change of the effective mass (Figure 2) with respect to magnetic field by setting (for the constant chemical potential)
Figure 1. Rate of change of the effective mass with respect to the magnetic field.
Figure 2. Plot of the rate pf change of the effective mass with respect tothe magnetic field as a function of the magnetic field.
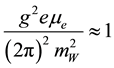 (6)
(6)
The plot of Equation (1) indicates that the effective mass of neutrino becomes significant only for an extremely large magnetic field (Millions of Tesla) which is only possible for extremely large chemical potential of electrons. Just to look at the magnetic field dependence, we choose constant density of electrons associated with the tremendously large chemical potential. Stable systems usually cannot acquire such high values of density and magnetic fields, however, these conditions cannot be ruled out during the process of generation of superdense stars.
It can be clearly seen from the graph that the magnetic field effect is only significant for extremely large magnetic field which is only possible for unusually dense systems.
3. Dirac Neutrino
Induced magnetic dipole moment is associated with neutral Dirac particle through its interaction with the corresponding charged lepton. In the MESM, the lepton flavor mixing is not allowed just as the SEWM. Right- handed neutrino is the only additional singlet in this model and is inert in nature. So all the Feynman rules are obeyed and basic diagrams of the SEWM are studied. Dirac neutrino has a nonzero magnetic moment in vacuum [4] . The boson propagator in the real-time formalism can be written as [12] - [18]
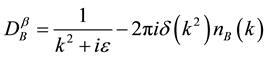 (7a)
(7a)
and the fermion propagator as,

with the Bose-Einstein distribution,

for massless vector bosons. This automatically leads to the vanishing mass density and hence the chemical potential. The Fermi-Dirac distribution is given by [20]

such that the chemical potential of fermions is always equal and opposite to the corresponding anti-fermions in CP symmetric background. However, Equation (8b) can still work (for comparable values of particle-antiparticle concentration) even if CP symmetry breaks. Since all the particle species are in thermal equilibrium, it is convenient to expand the distribution functions in powers of


and in the limit of 

for particles. Distribution functions for antiparticles, in the same approximations give

and



where, p is the magnitude of the three momentum of the particles. In the presence of the constant background magnetic field, it reads out to be [19]

where n corresponds to the Landau Levels. We ignore the polarization effects for the moment. The electromagnetic properties of neutrinos can be derived from the radiative decay of neutrino 


in usual notation with




where, 







and

where, q on the right-hand side of the equation corresponds to the magnitude of three-momentum vector q, and 


such that



with,



for 




The integrals





Equation (19) shows that the first two Equations (19a) and (19b) give nonzero values of 



for negligible antiparticles background. However, in CP-symmetric background, we can write Equations (20) as




such that, in the limit
or in other words the function




whereas,

In the high density regime, at 

and

Integrals of Equations (12) help to understand the nature of the background contributions. At high temperatures, the background contributions due to fermion and anti-fermion distributions are approximately equal and hence they cancel each other such that

At high densities, however, particle and antiparticle contribution need not to be the same all the time which implies that
In the CP symmetric dense background, the chemical potential of the fermions is equal and opposite to the chemical potential of the anti-fermions. This is the situation where again the contribution due to fermions background would not be the same as the anti-fermion contribution because of the different sign of the chemical potential 
The magnetic moment of neutrino can simply be obtained from the bubble diagram of the plasmon decay in the MSM. This contribution can be written as

In the standard notation of particle physics. We approximate the W propagator as 


with


where

Figure 3 gives a plot of magnetic moment as a function of temperature.
In the limit


where as,
Equation (34) indicates that the magnetic dipole moment of neutrino does not change much with the chemical potential 


Figure 3. Temperature dependent part of the magnetic moment of νe as a function of temperature.
Figure 4. A plot of magnetic moment as a function of chemical potential in units of electron mass in MESM.
And giving the magnetic moment in the units of the Bohr Magneton as,





In the extended standard models like HDM, the individual lepton no. is not conserve so the FTD corrections to the magnetic moment of neutrino could be different because we have to add new individual lepton number violating diagrams. The additional background FTD corrections to the magnetic moment of neutrino come out to be [6] [10]

with
Thermal corrections in Equation (36) are not only too small but negative which actually give a further decrease. 
at
Figure 5. A plot of magnetic moment as a function of chemical potential in units of electron mass in HDM.
Majorana Neutrino
The magnetic moment of neutrino changes strongly with chemical potential. It is well-known that the properties of Majorana neutrinos are different from that of Dirac neutrino. So, it cannot have the dipole moment as we describe for Dirac neutrino. However, it can have a transition magnetic dipole moment. Similarly the neutrinos of the SUSY models canalso have the transition magnetic moment. Riotto [21] has claimed that a large class of models where charged scalar boson couple to leptons can provide the magnetic moment of electron type neutrino as large as 10−12 Bohr Magneton, which can play a relevant role in different astrophysical phenomenon. However, these extended standard models are constructed to get the required value of magnetic moment but the direct testing of the model is not easy. However, effective mass of Weyl neutrino could be considered a natural solution with the effective mass. Magnetic moment of different flavor neutrinos will then depend on the chemical potential of the corresponding charged fermions and their corresponding statistical conditions.
Majorana neutrinos undergo seesaw mechanism and it can acquire transition magnetic moment as the lepton number conservation is always violated. Like all other models, form factors are induced through radiative corrections. For Majorana particles, radiative corrections are model dependent. A comparison with MESM is not meaningful in the presence of a larger particle sectors as well as different conservation rules of the models with Majorana neutrinos. Heavy neutrinos, seesaw mechanism and heavy scalars with supersymmetric partners [21] -[23] make situation much more different. So the calculations of form factors of neutrino is model dependent and has to be evaluated in different rages of temperature and chemical potential separately.
4. Results and Discussions
Magnetic moment is one of the electromagnetic properties of matter and is proportional to mass.
Values of magnetic moments for different flavors of neutrinos in vacuum are given as
There is no background correction for massless neutrinos even at high temperatures, as temperature does not contribute to the effective mass of massless particles. The QED type radiative corrections are only important below the decoupling temperatures [24] [25] . Therefore, we study the magnetic moment below
Figure 6. Chemical potential corrections to the magnetic moment of electron type neutrino for MESM(solid line) and HDM(broken line).
the effective mass of neutrino is generated by the coupling of neutrino with the extremely dense background with constant magnetic field as is given in Equation (1). Rate of change of mass also depends on the strength of the magnetic field and is given in Equation (2). Figure 1 and Figure 2 show that the effective mass does not change significantly with the magnetic field until and unless this field is extremely large, really close to the threshold value, where it can go to infinity. However, the rate of change of mass (Figure 2) is even slowly varying as compared with the effective mass (Figure 1) itself.
For Dirac type of mass of neutrino in the MESM, the charged current contribution is nonzero at all temperatures and density and it is proportional to the mass of neutrino [4] , as expected. This contribution comes from the bubble diagram and corresponds to charged current interaction. Tadpole diagram of neutral current interaction does not contribute, as particle-antiparticle behavior is exactly the same at finite temperatures. However, the high density contributions (with extremely large values of
It is clear from the above results that the temperature corrections are really significant in the MESM only. HDM gives a negligibly small negative contribution, so its effect is the decrease instead of increased magnetic moment. However, the HDM pushes the magnetic moment limit faster to required values at chemical potential as compared with the MESM. A comparison of magnetic moment in HDM (dotted Line) and MESM (solid Line) is given in Figure 6.
The above analysis shows that the magnetic dipole moment of electron type neutrinos does not depend significantly on temperature, so thermal corrections do not give enough corrections to touch the cosmological limit [6] . However, chemical potential contribution to the magnetic moment is non-ignorable, even when chemical potential is a little more than the electron mass. Figure 6 shows that the density effect (or chemical potential dependence) is more significant in the extended Higgs sector with individual lepton number violation. It gives enough motivation to study the statistical corrections to the magnetic moment of neutrino in Supersymmetric models to look for an appropriate solution to some of the cosmological issues. This result is more relevant for the superdense stars such as neutron stars [26] or magnetars where magnetic field is extremely high and apparently small contribution is not insignificant. However, the magnetic moment of neutrino and its thermal corrections are negligible in the early universe and do not give significant contribution to lepton scatterings [27] [28] in the early universe.
References
- Mohapatra, R.N. and Pal, P.B. (1991) Massive Neutrinos in Physics and Astrophysics. World Scientific Publication. http://dx.doi.org/10.1142/1246
- Schechter, J. and Valle, W.F. (1981) Majorana Neutrinos and Magnetic Fields. Physical Review D, 24, 1883. http://dx.doi.org/10.1103/PhysRevD.24.1883
- Roberts, B.L. and Marciano, W.J., Eds. (2010) Lepton Dipole Moments. World Scientific. http://www.worldscientific.com/worldscibooks/10.1142/7273
- Lee, B.W. and Shrock, R.E. (1977) Natural Suppression of Symmetry Violation in Gauge Theories: Muon- and Electron-Lepton-Number Nonconservation. Physical Review D, 16, 1444. http://dx.doi.org/10.1103/PhysRevD.16.1444
- Masood, S.S. (1993) Neutrino Physics in Hot and Dense Media. Physical Review D, 48, 3250. http://dx.doi.org/10.1103/PhysRevD.48.3250
- Masood, S.S. (1995) Magnetic Moment of Neutrinos in the Statistical Background. Astroparticle Physics, 4, 189-194. http://dx.doi.org/10.1016/0927-6505(95)00031-4
- Kajita, T. (1999) Atmospheric Neutrino Results from Super-Kamiokande and Kamiokande―Evidence for νμ Oscillations. Nuclear Physics B―Proceedings Supplements, 77, 123-132. http://arxiv.org/pdf/hep-ex/9810001v1.pdf http://dx.doi.org/10.1016/S0920-5632(99)00407-7
- Koshiba, M. (1998) Kamiokande and Superkamiokande. Fifth School on Non-Accelerator Particle Astrophysics, Abdus Salam ICTP, Trieste, Italy.
- http://www-sk.icrr.u-tokyo.ac.jp/whatsnew/DOC-20110615/KEK110613english.pdf
- Babu, K.S. and Mathur, V.S. (1987) Magnetic Moments of Dirac and Majorana Neutrinos. Physics Letters B, 196, 218- 222. http://dx.doi.org/10.1016/0370-2693(87)90607-1
- Fukujita, M. and Yanagida, T. (1987) Particle-Physics Model for Voloshin-Vysotsky-Okun Solution to the Solar-Neutrino Problem. Physical Review Letters, 58, 1807. http://dx.doi.org/10.1103/PhysRevLett.58.1807
- Landsman, P. and van Weert, Ch.G. (1987) Real- and Imaginary-Time Field Theory at Finite Temperature and Density. Physics Reports, 145, 141-249. http://dx.doi.org/10.1016/0370-1573(87)90121-9
- Ahmed, K. and Masood, S.S. (1987) Physical Review D, 35, 1861.
- Ahmed, K. and Masood, S.S. (1987) Finite-Temperature and -Density Renormalization Effects in QED. Physical Review D, 35, 4020. http://dx.doi.org/10.1103/PhysRevD.35.4020
- Ahmed, K. and Masood, S.S. (1991) Vacuum Polarization at Finite Temperature and Density in QED. Annals of Physics, 164, 460-473. http://dx.doi.org/10.1016/0003-4916(91)90066-H
- Masood, S.S. (1991) Photon Mass in the Classical Limit of Finite-Temperature and -Density QED. Physical Review D, 44, 3943. http://dx.doi.org/10.1103/PhysRevD.44.3943
- Masood, S.S. (1993) Renormalization of QED in Superdense Media. Physical Review D, 47, 648. http://dx.doi.org/10.1103/PhysRevD.47.648
- Masood, S.S. and Haseeb, M. (1995) Gluon Polarization at Finite Temperature and Density. Astroparticle Physics, 3, 405-412.
- Perez-Martinez, A., et al. (2002) Effective Magnetic Moment of Neutrinos in Strong Magnetic Fields. Revista Mexicana De Fisica, 48, 501.
- Levinson, E.J. and Boal, D.H. (1985) Self-Energy Corrections to Fermions in the Presence of a Thermal Background. Physical Review D, 31, 3280. http://dx.doi.org/10.1103/PhysRevD.31.3280
- Riotto, A. (1994) Thermal Background Corrections to the Neutrino Electromagnetic Vertex in Models with Charged Scalar Bosons. Physical Review D, 50, 2139-2147. http://dx.doi.org/10.1103/PhysRevD.50.2139
- Kaplan, D.L., Kulkarni, S.R., van Kerkwijk, M.H., Rothschild, R.E., Lingenfelter, R.L., Marsden, D., et al. (2001) Hubble Space Telescope Observations of SGR 0526-66: New Constraints on Accretion and Magnetar Models. The Astrophysical Journal, 556, 399-407. http://dx.doi.org/10.1086/323516
- Aboubrahim, A., Ibrahim, T., Itani, A. and Nath, P. (2014) Large Neutrino Magnetic Dipole Moments in MSSM Extensions. Physical Review D, 89, Article ID: 055009. http://dx.doi.org/10.1103/PhysRevD.89.055009
- Masood, S.S. (2014) Nucleosynthesis in Hot and Dense Media. Journal of Modern Physics, 5, 296-308.
- Masood, S.S. (2014) Renormalization of QED near Decoupling Temperature. Physics Research International, 2014, Article ID: 489163.
- Chaichian, M., Masood, S.S., Montonen, C., Pérez Martínez, A. and Pérez Rojas, H. (2000) Quantum Magnetic Collapse. Physical Review Letters, 84, 5261-5264. http://dx.doi.org/10.1103/PhysRevLett.84.5261
- Masood, S.S. and Qader, M. (1992) Finite-Temperature and -Density Corrections to Electroweak Processes. Physical Review D, 46, 5110-5116. http://dx.doi.org/10.1103/PhysRevD.46.5110
- Masood, S.S. (2001) Scattering of Leptons in Hot and Dense Media. arXiv:hep-ph/0108126v2.





















