Open Journal of Applied Sciences
Vol.4 No.1(2014), Article ID:41857,5 pages DOI:10.4236/ojapps.2014.41001
An Algorithm to Determine RBFNN’s Center Based on the Improved Density Method
School of Science, Shandong University of Technology, Zibo, China
Email: sdlgzmw_11@163.com, zyp0543@163.com
Received 26 September 2013; revised 1 November 2013; accepted 9 November 2013
ABSTRACT
It takes more time and is easier to fall into the local minimum value when using the traditional full-supervised learning algorithm to train RBFNN. Therefore, the paper proposes one algorithm to determine the RBFNN’s data center based on the improvement density method. First it uses the improved density method to select RBFNN’s data center, and calculates the expansion constant of each center, then only trains the network weight with the gradient descent method. To compare this method with full-supervised gradient descent method, the time not only has obvious reduc-tion (including to choose data center’s time by density method), but also obtains better classifica-tion results when using the data set in UCI to carry on the test to the network.
Keywords: Radial Basis Function Neural Network; Data Center; Expansion Constant; Density Method; Full-Supervised Algorithm

1. Introduction
T Radial Basis Function Neural Network (RBFNN) is a forward neural network of good performance. It has faster learning rate than BP neural network and there is no local minimum problem. It can find the exact nonlinear system’s mapping as long as there are enough samples. So it is widely used like linear approximation, data mining and image processing, etc.
The nonlinear ability of RBFNN is mainly reflected in the radial function of the hidden layer whose property is determined by its data center. Thus, the key problem is to determine the number, position and width of the radial function to construct a RBFNN. Domestic and foreign scholars have studied a variety of methods to determine the center of radial basis function [1-7]. Overall, the methods to determine the data center can be divided into two categories: supervised method and unsupervised method. In terms of supervised methods, it needs us to specify the number of the hidden layer. This requires some prior knowledge. But in most cases, we have only large amounts of data and we can’t clearly know their class. So it needs us to determine the centers to use the unsupervised method. In this paper, we proposed an improved density method—a dynamic clustering algorithm in mathematical statistics to select the data center of RBFNN and trained the weight value with gradient descent method. The simulation result is better.
This article is organized according to the following contents: Part 2 introduces the basic theory of RBFNN; Part 3 and Part 4 propose the specific algorithm; Part 5 is the experiments and analysis; Finally, conclusions.
2. The Basic Theory of RBFNN
RBFNN is a three-layer feed-forward network, and it has only one hidden layer whose activation function is the radial basis function, for example, the Gauss function. Its output layer is a simple linear function. The network structure of RBFNN shown in Figure 1.
Let 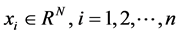 is the
is the 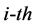 learning sample, each sample is N-dimensional, and then RBFNN’s network output can be expressed by formula (1) and (2):
learning sample, each sample is N-dimensional, and then RBFNN’s network output can be expressed by formula (1) and (2):
 (1)
(1)
 (2)
(2)
where yi is the network actual output according to the  learning sample; wik is the weight value of the
learning sample; wik is the weight value of the 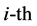 hidden layer node to the
hidden layer node to the  output node;
output node;
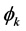 is the Gauss Radial Function; ck is the
is the Gauss Radial Function; ck is the  data center in the hidden layer;
data center in the hidden layer;
 represents the Euclidean distance; σk is the
represents the Euclidean distance; σk is the 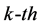 width of the radial basis function.
width of the radial basis function.
Thus, RBFNN structure determination process is the process of seeking the three network parameters-w, c, σ. This paper determines the data center by the improved density method and its expansion constant and trains its weight value by gradient descent method.
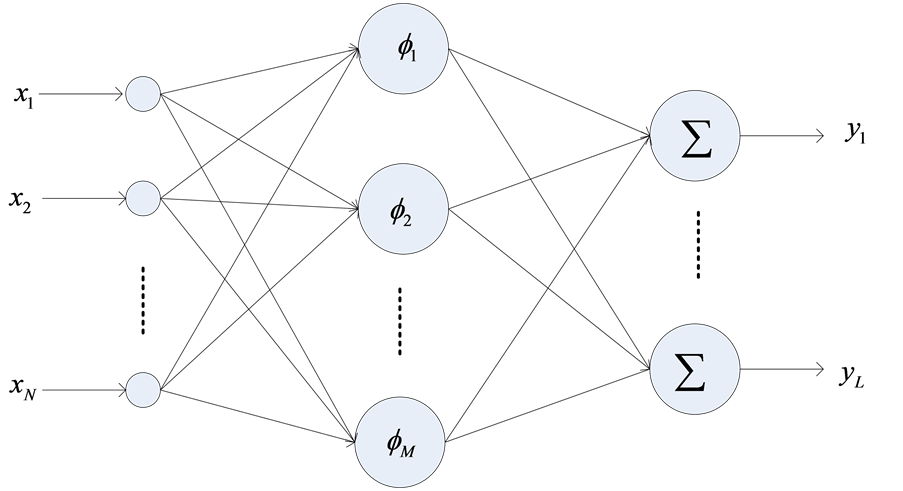
Figure 1. The network structure of RBFNN.
3. The Original Density Method to Choose the Data Center of RBFNN
The Original density method is a dynamic clustering algorithm. It is different from the K-means clustering algorithm. The Samples is divided into M class in advance in K-means algorithm, and randomly select M data centers. Then it calculates the Euclidean distance between each sample and each data center and the nearest sample will be classified as a class. Finally updates the cluster centers by different method. This method has obvious drawbacks. We don’t know how many data centers and don’t know their positions. However, the density method just need two value—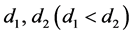 , centre of sphere to each sample, d to be the sphere of radial, and the number of samples falling within the sphere is called the density of this point. The maximum density of the sample is selected as the first cluster center, the second largest density of the sample as a candidate cluster centers, then calculate the distance with previous cluster center. We don’t choose it as the cluster center if the distance is less than d2, instead choose. And so on, we obtain some data centers of gradually smaller density and the distance larger than d2 away from each other. The experience has shown that generally
, centre of sphere to each sample, d to be the sphere of radial, and the number of samples falling within the sphere is called the density of this point. The maximum density of the sample is selected as the first cluster center, the second largest density of the sample as a candidate cluster centers, then calculate the distance with previous cluster center. We don’t choose it as the cluster center if the distance is less than d2, instead choose. And so on, we obtain some data centers of gradually smaller density and the distance larger than d2 away from each other. The experience has shown that generally . Specific steps are as follows:
. Specific steps are as follows:
Let sample set as 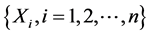
1) Given ,calculate the density-ρ for each sample, a deposit in set A, select the samples-ρmax of the largest density to compose a group of cluster centers, and stored in set C;
,calculate the density-ρ for each sample, a deposit in set A, select the samples-ρmax of the largest density to compose a group of cluster centers, and stored in set C;
2) Initialize classification. The Samples are classified according to minimum distance. Calculate the Euclidean distance between the remaining samples and the cluster center in set C and compare with d2: we classify as a class of cluster center if the distance is less than d2 and instead is not classified. Thus, we obtain initial classification set B.
3) Modify category. To calculate the center of each cluster, go to (d) if the result is the same as origin cluster center. Otherwise, the center of each cluster is as new cluster center, go to 2)
4) Cluster is End. We obtain the finally cluster center set B. Store the element number of set B in M, and signify 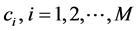 as the cluster center vector.
as the cluster center vector.
Using the above steps, we obtained RBFNN hidden layer node number and center vectors, which the 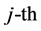 data width is from literature [8], but we improved it as follow formula (3):
data width is from literature [8], but we improved it as follow formula (3):
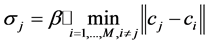 (3)
(3)
where the parameter β is a constant greater or than equal 1 and can be appropriately selected in the experiment.
Thus, we get all parameters of RBFNN.
4. The RBFNN’s Training Algorithm Based on Improved Density Method
4.1. Steps of Algorithm
Obtained the hidden layer structural parameters by Part 2 in this paper, we can get the RBFNN’s training algorithm based on improved density method. The steps are as follows:
1) We get the number M of hidden layer nodes, center vector 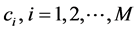 and data width
and data width  by the algorithm in Part 2.
by the algorithm in Part 2.
2) Initialize the weight from hidden layer to output layer ωj and just optimize weight by the gradient descent method. The procedure is as follows:
a) Define the objective function, as follow formula (4)
 (4)
(4)
where n is sample number, ei is the error signal when we input the 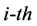 sample. It is shown as follow formula (5):
sample. It is shown as follow formula (5):
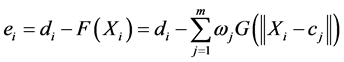 (5)
(5)
b) Get the weight correction and revise weight. Weight correction is obtained according to formula (6) as follow:
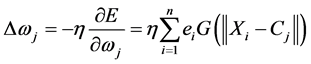 (6)
(6)
formula (7) of weight correction as shown below:
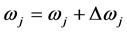 (7)
(7)
4.2. Analysis of Algorithmic Time Complexity
After the hidden layer parameters obtained can be intuitively seen from the above algorithm, we no longer train RBFNN’s centers and width, and weight training only. It is equivalent to linear optimization problems, the computation greatly reduced compared with the full-supervised learning algorithm. For the full-supervised learning algorithm we need train weights, data centers, and the constant expansion of radial basis functions to learn at the same time. It is a very complicated nonlinear optimization problem. The specific analysis is as follows:
Assuming the total number of training sample is P, and we randomly select M1 data centers by the full-supervised algorithm and M2 by the improved algorithm proposed by this paper. When we use the full-supervised algorithm, we need apply the formula (8), (9) and (6) to calculate data center, width and weight. The calculate amount is 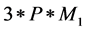 multiplication. But the calculate amount of the improved density method is
multiplication. But the calculate amount of the improved density method is  multiplication, which
multiplication, which  is the times that used to calculate the distance. That M1 and M2 is almost same. But the time to compute
is the times that used to calculate the distance. That M1 and M2 is almost same. But the time to compute  is less than
is less than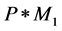 . So in theory, the time complexity of the improved density method to train RBFNN is less than the full-supervised algorithm.
. So in theory, the time complexity of the improved density method to train RBFNN is less than the full-supervised algorithm.
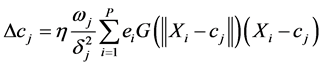 (8)
(8)
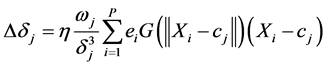 (9)
(9)
(where, ).
).
5. Experiment and Analysis
We use data sets Iris, Diabetes and Letter three datasets from UCI [9] to test the method on this article. The information of data sets is shown in Table1 We set Iris data set as an example. First we disarrange the data, and then classify to them and obtain data centers by the improved density method, and last train weight by the gradient descent method. The following are the specific parameters and experimental results.
Let ,
,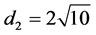 . We reclassify the disarranged data and get 5 category by the density method. So the network structure of RBFNN is identified as 4-5-1. Let
. We reclassify the disarranged data and get 5 category by the density method. So the network structure of RBFNN is identified as 4-5-1. Let  when calculate the RBF center. Get the corresponding data width
when calculate the RBF center. Get the corresponding data width 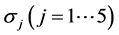 by formula (3). Let the learning rate
by formula (3). Let the learning rate 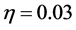 when train weight by the gradient descent method. Comparing with the full-supervised algorithm, the results are shown in Table 2 below:
when train weight by the gradient descent method. Comparing with the full-supervised algorithm, the results are shown in Table 2 below:
The experiment environment is as follows:
CPU: dual-core, clocked at 1.83 GHZ; Memory: 1 GHZ; OS: Windows XP; Software: Matlab R2009a.
As previous chapter 3.2 analysis, although the time complexity of two algorithm is both O(n2), the result of repeated testing shows the time-consuming of the improved algorithm is less than the full-supervised algorithm.
Table 2. Comparison of experiment results.
Note: acc stands for accuracy; The t(s) by the improved algorithm includes the time to compute data centers by the improved density method.
This confirms our previous analysis. When we test the letter dataset, 2 GB virtual memory settings on your computer does not meet the requirements. It leads the computer into the crash state. But it works well using of the improved algorithm.
6. Summary
This paper proposes an algorithm based on improved density method to choose data centers of RBFNN. Firstly, the density method is used to classify training samples and get the data centers, data width and category of data center. Then, we use these parameters to construct the RBFNN and then just train weight by the gradient descent method. It is equivalent to linear optimization problems. Finally, we obtain the RBFNN of better performance. However, the full-supervised learning algorithm is a very complex nonlinear optimization problem and it requires all parameters of RBFNN to learn simultaneously. So it is easy to make the result into the local minimum. In the classification of the three UCI datasets: Iris, Diabetes, and letter, the proposed algorithm obtains a better classification result.
References
[1] Chen, S., Cowan, C.F. and Grant, P.M. (1991) Orthogonal least squares learning algorithms for radial basis function networks. IEEE Transactions on Neural Networks, 2, 302-309. http://dx.doi.org/10.1109/72.80341
[2] Gomm, J.B. and Yu, D.L. (2000) Selecting radial basis function network centers with recursive orthogonal least squares training. IEEE Transactions on Neural Networks, 11, 306-314. http://dx.doi.org/10.1109/72.839002
[3] Han, M. and Guo, W. (2004) The full-supervised learning algorithm of radial basis function neural network. Chinese Journal of Science Instrument, 25, 454-457.
[4] Toh, K.-A. and Mao, K.Z. (2002) A global transformation approach to RBF Neural Network learning. Proceedings of 16th International Conference on Pattern Recognition (ICPR’02), 2, 96-99.
[5] Wei, H.K. and Ding, W.M. (2002) Dynamic method for designing RBF neural networks. Control Theory & Application, 19, 673-680.
[6] Wettschereck, D. and Dietterich, T. (1992) Improving the performance of radial basis function networks by learning center locations. Moody, J., Hanson, S. and Lippman R., Eds., Advances in Neural Information Processing Systems 4, Morgan Kaufmann Publishers, San Mateo.
[7] Tarassenko, L. and Roberts, S. (1994) Supervised and unsupervised learning in radial basis function classifiers. IEE Proceedings of Vision, Image and Signal Processing, 141, 210-216. http://dx.doi.org/10.1049/ip-vis:19941324
[8] Han, L.Q. (2006) Artificial neural network tutorial. Beijing University of Posts and Telecommunications Press, Beijing, 12Ver 1, 137.
[9] Web Site of UCI Machine Learning Repository. (2002) University of California, Irvine. http://www.1.ics.uci.edu/~mlearn/MLRepository.html


